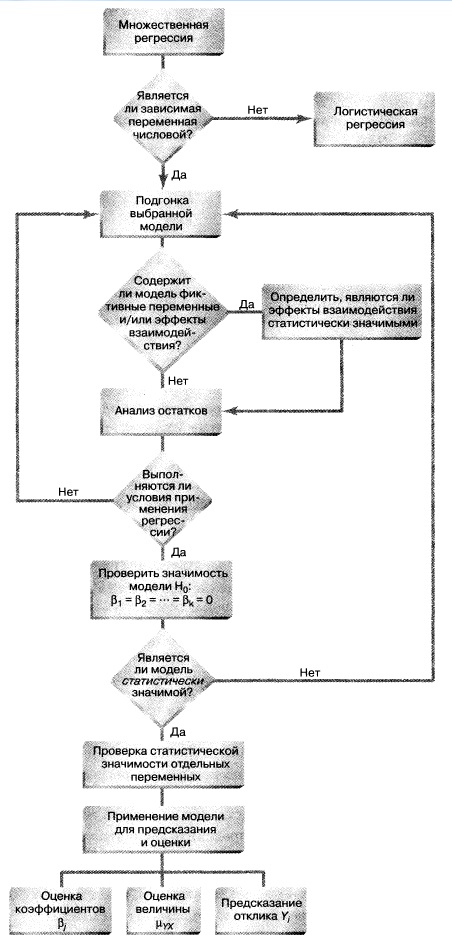
Уравнение множественной регрессии строится когда

Уравнение множественной регрессии

Назначение сервиса . С помощью онлайн-калькулятора можно найти следующие показатели:

• уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
• множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;

Кроме этого проводится проверка на автокорреляцию остатков и гетероскедастичность.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Отбор факторов обычно осуществляется в два этапа:

1. теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
2. количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа — однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
3. Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность — тесная линейная связь между факторами.

Пример . Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
К исходной матрице X добавим единичный столбец, получив новую матрицу X

1	5	14.5
1	12	18
1	6	12
1	7	13
1	8	14

Матрица Y

9

13

16

14

21

Транспонируем матрицу X, получаем X T :

1	1	1	1	1
5	12	6	7	8
14.5	18	12	13	14

Умножаем матрицы, X T X =

5 38 71,5 38 318 563,5 71,5 563,5 1043,25

В матрице, (X T X) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X

Умножаем матрицы, X T Y =

73 563 1032,5

Находим обратную матрицу (X T X) -1

13.99	0.64	-1.3
0.64	0.1	-0.0988
-1.3	-0.0988	0.14

Вектор оценок коэффициентов регрессии равен

(X T X) -1 X T Y = y(x) =

13,99 0,64 -1,3 0,64 0,1 -0,0988 -1,3 -0,0988 0,14

*

73 563 1032,5

=

34,66 1,97 -2,45

Получили оценку уравнения регрессии: Y = 34.66 + 1.97X₁-2.45X₂
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности. Для ее проверки используют F-критерий Фишера.
R 2 = 1 — s 2 _e/∑(y_i — y_ср) 2 = 1 — 33.18/77.2 = 0.57
F = R 2 /(1 — R 2 )*(n — m -1)/m = 0.57/(1 — 0.57)*(5-2-1)/2 = 1.33
Табличное значение при степенях свободы k₁ = 2 и k₂ = n-m-1 = 5 — 2 -1 = 2, Fkp(2;2) = 19
Поскольку фактическое значение F = 1.33 Пример №2 . Приведены данные за 15 лет по темпам прироста заработной платы Y (%), производительности труда X₁ (%), а также по уровню инфляции X₂ (%).

Год	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
X1	3,5	2,8	6,3	4,5	3,1	1,5	7,6	6,7	4,2	2,7	4,5	3,5	5,0	2,3	2,8
X2	4,5	3,0	3,1	3,8	3,8	1,1	2,3	3,6	7,5	8,0	3,9	4,7	6,1	6,9	3,5
Y	9,0	6,0	8,9	9,0	7,1	3,2	6,5	9,1	14,6	11,9	9,2	8,8	12,0	12,5	5,7

Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .

Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),

После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X₁ + 1.4798X₂
Скачать.

Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).

Пример №3 .
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.

ВВП	16331,97	16763,35	17492,22	18473,83	19187,64	20066,25	21281,78	22326,86	23125,90
Потребление в текущих ценах	771,92	814,28	735,60	788,54	853,62	900,39	999,55	1076,37	1117,51
Инвестиции в текущих ценах	176,64	173,15	151,96	171,62	192,26	198,71	227,17	259,07	259,85

Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).

Пример №4 . На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:

1. Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.
2. Рассчитать частные коэффициенты эластичности. Сделать вывод.
3. Определить стандартизованные коэффициенты регрессии (b-коэффициенты). Сделать вывод.
4. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
5. Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.

Решение. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X

1	3.9	10
1	3.9	14
1	3.7	15
1	4	16
1	3.8	17
1	4.8	19
1	5.4	19
1	4.4	20
1	5.3	20
1	6.8	20
1	6	21
1	6.4	22
1	6.8	22
1	7.2	25
1	8	28
1	8.2	29
1	8.1	30
1	8.5	31
1	9.6	32
1	9	36

Матрица Y

7
7
7
7
7
7
8
8
8
10
9
11
9
11
12
12
12
12
14
14

Матрица X T

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3.9	3.9	3.7	4	3.8	4.8	5.4	4.4	5.3	6.8	6	6.4	6.8	7.2	8	8.2	8.1	8.5	9.6	9
10	14	15	16	17	19	19	20	20	20	21	22	22	25	28	29	30	31	32	36

Умножаем матрицы, (X T X)

Умножаем матрицы, (X T Y)

Находим определитель det(X T X) T = 139940.08
Находим обратную матрицу (X T X) -1

Уравнение регрессии
Y = 1.8353 + 0.9459X ₁ + 0.0856X ₂
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y — X*s

0.62
0.28
0.38
0.01
0.11
-1
-0.57
0.29
-0.56
0.02
-0.31
1.23
-1.15
0.21
0.2
-0.07
-0.07
-0.53
0.34
0.57

se 2 = (Y — X*s) T (Y — X*s)
Несмещенная оценка дисперсии равна

Оценка среднеквадратичного отклонения равна

Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1

k(x) = 0.36

0,619 -0,0262 -0,0183 -0,0262 0,126 -0,0338 -0,0183 -0,0338 0,0102

=

0,222 -0,00939 -0,00654 -0,00939 0,0452 -0,0121 -0,00654 -0,0121 0,00366

Дисперсии параметров модели определяются соотношением S 2 _i = K_ii, т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)

Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора х_i при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции — последовательно берутся пары yx1,yx2. , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции

Коэффициент детерминации
R 2 = 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая

Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл: T_табл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно

Построение парной регрессионной модели

Рекомендации к решению контрольной работы.

Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.

Пример №3 . Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x₁, дохода компании x₂ и объема инвестиций в расширение и модернизацию производства x₃. Исходные данные представлены выборкой объема n=50.

Тема I. Парная линейная регрессия
Постройте парные линейные регрессии — зависимости признака y от факторов x₁, x₂, x₃ взятых по отдельности. Для каждой объясняющей переменной:

1. Постройте диаграмму рассеяния (поле корреляции). При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).
2. Вычислите коэффициенты уравнения выборочной парной линейной регрессии (для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические») или надстройкой Пакет Анализа), коэффициент детерминации, коэффициент корреляции (функция КОРЕЛЛ), среднюю ошибку аппроксимации.
3. Запишите полученное уравнение выборочной регрессии. Дайте интерпретацию найденным в предыдущем пункте значениям.
4. Постройте на поле корреляции прямую линию выборочной регрессии по точкам .
5. Постройте диаграмму остатков.
6. Проверьте статистическую значимость коэффициентов регрессии по критерию Стьюдента (табличное значение определите с помощью функции СТЬЮДРАСПОБР) и всего уравнения в целом по критерию Фишера (табличное значение F_табл определите с помощью функции FРАСПОБР).
7. Постройте доверительные интервалы для коэффициентов регрессии. Дайте им интерпретацию.
8. Постройте прогноз для значения фактора, на 50% превышающего его среднее значение.
9. Постройте доверительный интервал прогноза. Дайте ему экономическую интерпретацию.
10. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемого фактора на показатель.

Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации и дайте ей интерпретацию.
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.

Введение в множественную регрессию

Рассматривая простую регрессию, мы сосредоточили внимание на модели, в которой для предсказания значения зависимой переменной, или отклика Y, использовалась лишь одна независимая, или объясняющая, переменная X. Однако во многих случаях можно разработать более точную модель, если учесть не одну, а несколько объясняющих переменных. По этой причине мы рассмотрим в этой заметке модели множественной регрессии, в которых для предсказания значения зависимой переменной используется несколько независимых переменных. [1]

Материал будет проиллюстрирован сквозным примером: прогнозирование объемов продаж компании OmniPower. Представьте себе, что вы — менеджер по маркетингу в крупной национальной сети бакалейных магазинов. В последние годы на рынке появились питательные батончики, содержащие большое количество жиров, углеводов и калорий. Они позволяют быстро восстановить запасы энергии, потраченной бегунами, альпинистами и другими спортсменами на изнурительных тренировках и соревнованиях. За последние годы объем продаж питательных батончиков резко вырос, и руководство компании OmniPower пришло к выводу, что этот сегмент рынка весьма перспективен. Прежде чем предлагать новый вид батончика на общенациональном рынке, компания хотела бы оценить влияние его стоимости и рекламных затрат на объем продаж. Для маркетингового исследования были отобраны 34 магазина. Вам необходимо создать регрессионную модель, позволяющую проанализировать данные, полученные в ходе исследования. Можно ли применить для этого модель простой линейной регрессии, рассмотренную в предыдущей заметке? Как ее следует изменить?

Модель множественной регрессии

Для маркетингового исследования в компании OmniPower была создана выборка, состоящая из 34 магазинов с приблизительно одинаковыми объемами продаж. Рассмотрим две независимые переменные — цена батончика OmniPower в центах (Х₁) и месячный бюджет рекламной кампании, проводимой в магазине, выраженный в долларах (Х₂). В этот бюджет входят расходы на оформление вывесок и витрин, а также на раздачу купонов и бесплатных образцов. Зависимая переменная Y представляет собой количество батончиков OmniPower, проданных за месяц (рис. 1).

Рис. 1. Месячный объем продажа батончиков OmniPower, их цена и расходы на рекламу

Скачать заметку в формате Word или pdf, примеры в формате Excel2013

Интерпретация регрессионных коэффициентов. Если в задаче исследуются несколько объясняющих переменных, модель простой линейной регрессии можно расширить, предполагая, что между откликом и каждой из независимых переменных существует линейная зависимость. Например, при наличии k объясняющих переменных модель множественной линейной регрессии принимает вид:

где β₀ — сдвиг, β₁ — наклон прямой Y, зависящей от переменной Х₁, если переменные Х₂, Х₃, … , Х_k являются константами, β₂ — наклон прямой Y, зависящей от переменной Х₂, если переменные Х₁, Х₃, … , Х_k являются константами, β_k — наклон прямой Y, зависящей от переменной Х_k, если переменные Х₁, Х₂, … , Х_k-1 являются константами, ε_i — случайная ошибка переменной Y в i-м наблюдении.

В частности, модель множественной регрессии с двумя объясняющими переменными:

где β₀ — сдвиг, β₁ — наклон прямой Y, зависящей от переменной Х₁, если переменная Х₂ является константой, β₂ — наклон прямой Y, зависящей от переменной Х₂, если переменная Х₁ является константой, ε_i — случайная ошибка переменной Y в i-м наблюдении.

Сравним эту модель множественной линейной регрессии и модель простой линейной регрессии: Y_i = β₀ + β₁X_i + ε_i. В модели простой линейной регрессии наклон β₁ представляет собой изменение среднего значения переменной Y при изменении значения переменной X на единицу и не учитывает влияние других факторов. В модели множественной регрессии с двумя независимыми переменными (2) наклон β₁ представляет собой изменение среднего значения переменной Y при изменении значения переменной X₁ на единицу с учетом влияния переменной Х₂. Эта величина называется коэффициентом чистой регрессии (или частной регрессии).

Как и в модели простой линейной регрессии, выборочные регрессионные коэффициенты b₀, b₁, и b₂ представляют собой оценки параметров соответствующей генеральной совокупности β₀, β₁ и β₂.

Уравнение множественной регрессии с двумя независимыми переменными:

(3) = b₀ + b₁X_1i + b₂X_2i

Для вычисления коэффициентов регрессии используется метод наименьших квадратов. В Excel можно воспользоваться Пакетом анализа, опцией Регрессия. В отличие от построения линейной регрессии, просто задайте в качестве Входного интервала Х область, включающую все независимые переменные (рис. 2). В нашем примере это $C$1:$D$35.

Рис. 2. Окно Регрессия Пакета анализа Excel

Результаты работы Пакета анализа представлены на рис. 3. Как видим, b₀ = 5 837,52, b₁ = –53,217 и b₂ = 3,163. Следовательно, = 5 837,52 –53,217X_1i + 3,163X_2i , где Ŷ_i — предсказанный объем продаж питательных батончиков OmniPower в i-м магазине (штук), Х_1i — цена батончика (в центах) в i-м магазине, Х_2i — ежемесячные затраты на рекламу в i-м магазине (в долларах).

Рис. 3. Множественная регрессия исследования объем продажа батончиков OmniPower

Выборочный наклон b₀ равен 5 837,52 и является оценкой среднего количества батончиков OmniPower, проданных за месяц при нулевой цене и отсутствии затрат на рекламу. Поскольку эти условия лишены смысла, в данной ситуации величина наклона b₀ не имеет разумной интерпретации.

Выборочный наклон b₁ равен –53,217. Это значит, что при заданном ежемесячном объеме затрат на рекламу увеличение цены батончика на один цент приведет к снижению ожидаемого объема продаж на 53,217 штук. Аналогично выборочный наклон b₂, равный 3,613, означает, что при фиксированной цене увеличение ежемесячных рекламных затрат на один доллар сопровождается увеличением ожидаемого объема продаж батончиков на 3,613 шт. Эти оценки позволяют лучше понять влияние цены и рекламы на объем продаж. Например, при фиксированном объеме затрат на рекламу уменьшение цены батончика на 10 центов увеличит объем продаж на 532,173 шт., а при фиксированной цене батончика увеличение рекламных затрат на 100 долл. увеличит объем продаж на 361,31 шт.

Интерпретация наклонов в модели множественной регрессии. Коэффициенты в модели множественной регрессии называются коэффициентами чистой регрессии. Они оценивают среднее изменение отклика Y при изменении величины X на единицу, если все остальные объясняющие переменные «заморожены». Например, в задаче о батончиках OmniPower магазин с фиксированным объемом рекламных затрат за месяц продаст на 53,217 батончика меньше, если увеличит их стоимость на один цент. Возможна еще одна интерпретация этих коэффициентов. Представьте себе одинаковые магазины с одинаковым объемом затрат на рекламу. При уменьшении цены батончика на один цент объем продаж в этих магазинах увеличится на 53,217 батончика. Рассмотрим теперь два магазина, в которых батончики стоят одинаково, но затраты на рекламу отличаются. При увеличении этих затрат на один доллар объем продаж в этих магазинах увеличится на 3,613 штук. Как видим, разумная интерпретация наклонов возможна лишь при определенных ограничениях, наложенных на объясняющие переменные.

Предсказание значений зависимой переменной Y. Выяснив, что накопленные данные позволяют использовать модель множественной регрессии, мы можем прогнозировать ежемесячный объем продаж батончиков OmniPower и построить доверительные интервалы для среднего и предсказанного объемов продаж. Для того чтобы предсказать средний ежемесячный объем продаж батончиков OmniPower по цене 79 центов в магазине, расходующем на рекламу 400 долл. в месяц, следует применить уравнение множественной регрессии: Y = 5 837,53 – 53,2173*79 + 3,6131*400 = 3 079. Следовательно, ожидаемый объем продаж в магазинах, торгующих батончиками OmniPower по цене 79 центов и расходующих на рекламу 400 долл. в месяц, равен 3 079 шт.

Вычислив величину Y и оценив остатки, можно построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика. Ранее мы рассмотрели эту процедуру в рамках модели простой линейной регрессии. Однако построение аналогичных оценок для модели множественной регрессии сопряжено с большими вычислительными трудностями и здесь не приводится.

Коэффициент множественной смешанной корреляции. Напомним, что модель регрессии позволяет вычислить коэффициент смешанной корреляции r 2 . Поскольку в модели множественной регрессии существуют по крайней мере две объясняющие переменные, коэффициент множественной смешанной корреляции представляет собой долю вариации переменной Y, объясняемой заданным набором объясняющих переменных:

где SSR – сумма квадратов регрессии, SST – полная сумма квадратов.

Например, в задаче о продажах батончика OmniPower SSR = 39 472 731, SST = 52 093 677 и k = 2. Таким образом,

Это означает, что 75,8% вариации объемов продаж объясняется изменениями цен и колебаниями объемов затрат на рекламу.

Анализ остатков для модели множественной регрессии

Анализ остатков позволяет определить, можно ли применять модель множественной регрессии с двумя (или более) объясняющими переменными. Как правило, проводят следующие виды анализа остатков:

• Распределение остатков по (рис. 4).
• Распределение остатков по Х_1i (рис. 5).
• Распределение остатков по Х_2i (рис. 5).
• Распределение остатков по времени.

Первый график (рис. 4а) позволяет проанализировать распределение остатков в зависимости от предсказанных значений . Если величина остатков не зависит от предсказанных значений и принимает как положительные так и отрицательные значения (как в нашем пример), условие линейной зависимости переменной Y от обеих объясняющих переменных выполняется. К сожалению, в Пакете анализа этот график почему-то не создается. Можно в окне Регрессия (см. рис. 2) включить Остатки. Это позволит вывести таблицу с остатками, а уже по ней построить точечный график (рис. 4).

Рис. 4. Зависимость остатков от предсказанного значения

Второй и третий график демонстрируют зависимость остатков от объясняющих переменных. Эти графики могут выявить квадратичный эффект. В этой ситуации необходимо добавить в модель множественной регрессии квадрат объясняющей переменной. Эти графики выводятся Пакетом анализа (см. рис. 2), если включить опцию График остатков (рис. 5).

Рис. 5. Зависимость остатков от цены и затрат на рекламу

Четвертый график применяется для проверки независимости данных, собранных в течение определенного времени. Для этого надо наблюдения расположить по времени, и построить зависимость предсказанного значения от времени. Поскольку в примере с OmniPower все измерения делались одновременно, такой график не применим. Для выявления положительной автокорреляции между остатками можно вычислить статистику Дурбина-Уотсона (подробнее см. соответствующий раздел заметки Простая линейная регрессия).

Проверка значимости модели множественной регрессии.

Убедившись с помощью анализа остатков, что модель линейной множественной регрессии является адекватной, можно определить, существует ли статистически значимая взаимосвязь между зависимой переменной и набором объясняющих переменных. Поскольку в модель входит несколько объясняющих переменных, нулевая и альтернативная гипотезы формулируются следующим образом: Н₀: β₁ = β₂ = … = β_k = 0 (между откликом и объясняющими переменными нет линейной зависимости), Н₁: существует по крайней мере одно значение β_j ≠ 0 (мжду откликом и хотя бы одной объясняющей переменной существует линейная зависимость).

Для проверки нулевой гипотезы применяется F-критерий – тестовая F-статистика равна среднему квадрату, обусловленному регрессией (MSR), деленному на дисперсию ошибок (MSE):

где F – тестовая статистика, имеющая F-распределение с k и n – k – 1 степенями свободы, k – количество независимых переменных в регрессионной модели.

Решающее правило выглядит следующим образом: при уровне значимости α нулевая гипотеза Н₀ отклоняется, если F > F_{U(k,n – k – 1)}, в противном случае гипотеза Н₀ не отклоняется (рис. 6).

Рис. 6. Сводная таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициентов множественной регрессии

Сводная таблица дисперсионного анализа, заполненная с использованием Пакета анализа Excel при решении задачи о продажах батончиков OmniPower, показана на рис. 3 (см. область А10:F14). Если уровень значимости равен 0,05, критическое значение F-распределения с двумя и 31 степенями свободы F_U(2,31) = F.ОБР(1-0,05;2;31) = равно 3,305 (рис. 7).

Рис. 7. Проверка гипотезы о значимости коэффициентов регрессии при уровне значимости α = 0,05, с 2 и 31 степенями свободы

Как показано на рис. 3, F-статистика равна 48,477 > F_U(2,31) = 3,305, а p-значение близко к 0,000 2,0395 или р = 0,0000 4,17), гипотеза Н₀ отклоняется, следовательно, учет переменной Х₁ (цены) значительно улучшает модель регрессии, в которую уже включена переменная Х₂ (затраты на рекламу).

Аналогично можно оценить влияние переменной Х₂ (затраты на рекламу) на модель, в которую уже включена переменная Х₁ (цена). Проведите вычисления самостоятельно. Решающее условие приводит к тому, что 27,8 > 4,17, и следовательно, включение переменной Х₂ также приводит к значительному увеличению точности модели, в которой учитывается переменная Х₁. Итак, включение каждой из переменных повышает точность модели. Следовательно, в модель множественной регрессии необходимо включить обе переменные: и цену, и затраты на рекламу.

Любопытно, что значение t-статистики, вычисленное по формуле (6), и значение частной F-статистики, заданной формулой (9), однозначно взаимосвязаны:

где а — количество степеней свободы.

Регрессионные модели с фиктивной переменной и эффекты взаимодействия

Обсуждая модели множественной регрессии, мы предполагали, что каждая независимая переменная является числовой. Однако во многих ситуациях в модель необходимо включать категорийные переменные. Например, в задаче о продажах батончиков OmniPower для предсказания среднемесячного объема продаж использовались цена и затраты на рекламу. Кроме этих числовых переменных, можно попытаться учесть в модели расположение товара внутри магазина (например, на витрине или нет). Для того чтобы учесть в регрессионной модели категорийные переменные, следует включить в нее фиктивные переменные. Например, если некая категорийная объясняющая переменная имеет две категории, для их представления достаточно одной фиктивной переменной X_d: X_d = 0, если наблюдение принадлежит первой категории, X_d = 1, если наблюдение принадлежит второй категории.

Для иллюстрации фиктивных переменных рассмотрим модель для предсказания средней оценочной стоимости недвижимости на основе выборки, состоящей из 15 домов. В качестве объясняющих переменных выберем жилую площадь дома (тыс. кв. футов) и наличие камина (рис. 11). Фиктивная переменная Х₂ (наличие камина) определена следующим образом: Х₂ = 0, если камина в доме нет, Х₂ = 1, если в доме есть камин.

Рис. 11. Оценочная стоимость, предсказанная по жилой площади и наличию камина

Предположим, что наклон оценочной стоимости, зависящей от жилой площади, одинаков у домов, имеющих камин и не имеющих его. Тогда модель множественной регрессии выглядит следующим образом:

где Y_i — оценочная стоимость i-гo дома, измеренная в тысячах долларов, β₀ — сдвиг отклика, X_1i,— жилая площадь i-гo дома, измеренная в тыс. кв. футов, β₁ — наклон оценочной стоимости, зависящей от жилой площади дома при постоянном значении фиктивной переменной, X_1i,— фиктивная переменная, означающая наличие или отсутствие камина, β₁ — наклон оценочной стоимости, зависящей от жилой площади дома при постоянном значении фиктивной переменной β₂ — эффект увеличения оценочной стоимости дома в зависимости от наличия камина при постоянной величине жилой площади, ε_i – случайная ошибка оценочной стоимости i-гo дома. Результаты вычисления регрессионой модели представлены на рис. 12.

Рис. 12. Результаты вычисления регрессионой модели для оценочной стоимости домов; получены с помощью Пакета анализа в Excel; для расчета использована таблица, аналогичная рис. 11, с единственным изменением: «Да» заменены единицами, а «Нет» – нулями

В этой модели коэффициенты регрессии интерпретируются следующим образом:

1. Если фиктивная переменная имеет постоянное значение, увеличение жилой площади на 1000 кв. футов приводит к увеличению предсказанной средней оценочной стоимости на 16,2 тыс. долл.
2. Если жилая площадь постоянна, наличие камина увеличивает среднюю оценочную стоимость дома на 3,9 тыс. долл.

Обратите внимание (рис. 12), t-статистика, соответствующая жилой площади, равна 6,29, а р-значение почти равно нулю. В то же время t-статистика, соответствующая фиктивной переменной, равна 3,1, а p-значение – 0,009. Таким образом, каждая из этих двух переменных вносит существенный вклад в модель, если уровень значимости равен 0,01. Кроме того, коэффициент множественной смешанной корреляции означает, что 81,1% вариации оценочной стоимости объясняется изменчивостью жилой площади дома и наличием камина.

Эффект взаимодействия. Во всех регрессионных моделях, рассмотренных выше, считалось, что влияние отклика на объясняющую переменную является статистически независимым от влияния отклика на другие объясняющие переменные. Если это условие не выполняется, возникает взаимодействие между зависимыми переменными. Например, вполне вероятно, что реклама оказывает большое влияние на объем продаж товаров, имеющих низкую цену. Однако, если цена товара слишком высока, увеличение расходов на рекламу не может существенно повысить объем продаж. В этом случае наблюдается взаимодействие между ценой товара и затратами на его рекламу. Иначе говоря, нельзя делать общих утверждений о зависимости объема продаж от затрат на рекламу. Влияние рекламных расходов на объем продаж зависит от цены. Это влияние учитывается в модели множественной регрессии с помощью эффекта взаимодействия. Для иллюстрации этого понятия вернемся к задаче о стоимости домов.

В разработанной нами регрессионной модели предполагалось, что влияние размера дома на его стоимость не зависит от того, есть ли в доме камин. Иначе говоря, считалось, что наклон оценочной стоимости, зависящей от жилой площади дома, одинаков у домов, имеющих камин и не имеющих его. Если эти наклоны отличаются друг от друга, между размером дома и наличием камина существует взаимодействие.

Проверка гипотезы о равенстве наклонов сводится к оценке вклада, который вносит в модель регрессии произведение объясняющей переменной X₁ и фиктивной переменной Х₂. Если этот вклад является статистически значимым, исходную модель регрессии применять нельзя. Результаты регрессионного анализа, включающего переменные Х₁, Х₂ и Х₃ = Х₁*Х₂ приведены на рис. 13.

Рис. 13. Результаты, полученные с помощью Пакета анализа Excel для регрессионной модели, учитывающей жилую площадь, наличие камина и их взаимодействие

Для того чтобы проверить нулевую гипотезу Н₀: β₃ = 0 и альтернативную гипотезу Н₁: β₃ ≠ 0, используя результаты, приведенные на рис. 13, обратим внимание на то, что t-статистика, соответствующая эффекту взаимодействия переменных, равна 1,48. Поскольку р-значение равно 0,166 > 0,05, нулевая гипотеза не отклоняется. Следовательно, взаимодействие переменных не имеет существенного влияния на модель регрессии, учитывающую жилую площадь и наличие камина.

Резюме. В заметке показано, как менеджер по маркетингу может применять множественный линейный анализ для предсказания объема продаж, зависящего от цены и затрат на рекламу. Рассмотрены различные модели множественной регрессии, включая квадратичные модели, модели с фиктивными переменными и модели с эффектами взаимодействия (рис. 14).

Рис. 14. Структурная схема заметки

[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 873–936

Множественная линейная регрессия (MLR)

Опубликовано 29.06.2021 · Обновлено 16.12.2021

Что такое Множественная линейная регрессия (MLR)?

Множественная линейная регрессия (MLR), также известная просто как множественная регрессия, – это статистический метод, который использует несколько независимых переменных для прогнозирования результата переменной ответа. Цель множественной линейной регрессии (MLR) – смоделировать линейную связь между независимыми (независимыми) переменными и ответной (зависимой) переменной.

По сути, множественная регрессия – это расширение обычной регрессии методом наименьших квадратов (МНК), которая включает более одной независимой переменной.

Формула и расчет множественной линейной регрессии

где для i=n наблюдений:
yi=зависимая переменная
xi=объясняющие переменные
β0=y-интерцепт (постоянный член)
βp=коэффициенты наклона для каждой объясняющей переменной
ϵ=член ошибки модели (также известный как остатки)

Основные выводы

• Множественная линейная регрессия (МЛР), также известная как множественная регрессия, – это статистический метод, который использует несколько объясняющих переменных для прогнозирования результата переменной ответа.
• Множественная регрессия является расширением линейной (OLS) регрессии, в которой используется только одна объясняющая переменная.
• MLR широко используется в эконометрике и финансовом анализе.
  О чем может рассказать множественная линейная регрессия (MLR)

Простая линейная регрессия – это функция, которая позволяет аналитику или статистику делать прогнозы относительно одной переменной на основе информации, которая известна о другой переменной. Линейная регрессия может быть использована только при наличии двух непрерывных переменных – независимой переменной и зависимой переменной. Независимая переменная – это параметр, который используется для расчета зависимой переменной или результата. Модель множественной регрессии распространяется на несколько объясняющих переменных.

Модель множественной регрессии основана на следующих предположениях:

Между зависимыми переменными и независимыми переменными существует линейная связь.
Независимые переменные не слишком сильно коррелируют друг с другом.
Наблюдения yi выбираются независимо и случайно из популяции.
Остатки должны быть нормально распределены со средним значением 0 и дисперсией σ.

Коэффициент детерминации (R-квадрат) – это статистическая метрика, которая используется для измерения того, насколько вариация результата может быть объяснена вариацией независимых переменных. R2 всегда увеличивается по мере добавления большего количества предикторов в модель MLR, даже если эти предикторы могут быть не связаны с переменной исхода.

Таким образом, R2 сам по себе не может быть использован для определения того, какие предикторы следует включить в модель, а какие исключить. R2 может быть только между 0 и 1, где 0 означает, что результат не может быть предсказан ни одной из независимых переменных, а 1 означает, что результат может быть безошибочно предсказан по независимым переменным.1

При интерпретации результатов множественной регрессии бета-коэффициенты действительны при постоянстве всех остальных переменных (“при прочих равных”). Результаты множественной регрессии могут быть представлены горизонтально в виде уравнения или вертикально в виде таблицы.2

Пример использования множественной линейной регрессии (MLR)

Например, аналитик может захотеть узнать, как движение рынка влияет на цену ExxonMobil (XOM). В этом случае линейное уравнение будет содержать значение индекса S&P 500 в качестве независимой переменной, или предиктора, и цену XOM в качестве зависимой переменной.

В действительности существует множество факторов, которые предсказывают исход события. Например, движение цены ExxonMobil зависит не только от общих показателей рынка. Другие факторы, такие как цена на нефть, процентные ставки и движение цен на нефтяные фьючерсы, могут влиять на цену XOM и цены акций других нефтяных компаний. Чтобы понять взаимосвязь, в которой присутствует более двух переменных, используется множественная линейная регрессия.

Множественная линейная регрессия (MLR) используется для определения математической взаимосвязи между рядом случайных переменных. Другими словами, MLR изучает, как несколько независимых переменных связаны с одной зависимой переменной. После определения того, что каждый из независимых факторов предсказывает зависимую переменную, информация о нескольких переменных может быть использована для создания точного прогноза об уровне их влияния на итоговую переменную. Модель создает зависимость в виде прямой (линейной) линии, которая наилучшим образом аппроксимирует все отдельные точки данных.3

Обращаясь к уравнению MLR, приведенному выше, в нашем примере:

yi = зависимая переменная – цена XOM
xi1 = процентные ставки
xi2 = цена на нефть
xi3 = значение индекса S&P 500
xi4 = цена нефтяных фьючерсов
B0 = y-интерцепт в нулевой момент времени
B1 = коэффициент регрессии, измеряющий изменение зависимой переменной на единицу при изменении xi1 – изменение цены XOM при изменении процентных ставок
B2 = коэффициент, измеряющий изменение зависимой переменной на единицу при изменении xi2 – изменение цены XOM при изменении цен на нефть

Оценки по методу наименьших квадратов, B0, B1, B2…Bp, обычно рассчитываются с помощью статистического программного обеспечения. В регрессионную модель можно включить любое количество переменных, в которой каждая независимая переменная обозначается номером – 1,2, 3, 4…p. Модель множественной регрессии позволяет аналитику предсказать результат на основе информации, полученной от нескольких объясняющих переменных.

Тем не менее, модель не всегда идеально точна, поскольку каждая точка данных может незначительно отличаться от результата, предсказанного моделью. Остаточное значение E, которое представляет собой разницу между фактическим и прогнозируемым результатом, включается в модель для учета таких незначительных изменений.

Предположим, что мы запустили нашу регрессионную модель цены XOM через программу статистических вычислений, которая выдает такой результат:

Аналитик интерпретирует этот результат так: если другие переменные остаются неизменными, то цена XOM увеличится на 7,8%, если цена на нефть на рынках вырастет на 1%. Модель также показывает, что цена XOM снизится на 1,5% после повышения процентных ставок на 1%. R2 показывает, что 86,5% изменений в цене акций Exxon Mobil можно объяснить изменениями в процентной ставке, цене на нефть, нефтяных фьючерсах и индексе S&P 500.

Разница между линейной и множественной регрессией

Обычная линейная квадратичная регрессия (OLS) сравнивает реакцию зависимой переменной на изменение некоторых объясняющих переменных. Однако редко бывает так, что зависимая переменная объясняется только одной переменной. В этом случае аналитик использует множественную регрессию, которая пытается объяснить зависимую переменную с помощью более чем одной независимой переменной. Множественная регрессия может быть линейной и нелинейной.

Множественная регрессия основана на предположении, что между зависимой и независимой переменными существует линейная связь. Также предполагается отсутствие значительной корреляции между независимыми переменными.