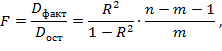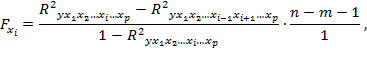Уравнение множественной регрессии значимо если f критерий

Множественная регрессия и корреляция

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ

2.1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Множественная регрессия — уравнение связи с несколькими независимыми переменными

где у— зависимая переменная (результативный признак);

— независимые переменные (факторы).

Для построения уравнения множественной регрессии чаще ис­пользуются следующие функции:

• линейная — ;

• степенная –

• экспонента —

• гипербола —

Можно использовать и другие функции, приводимые к линейно­му виду.

Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение кото­рой позволяет получить оценки параметров регрессии:

Для ее решения может быть применён метод определителей:

, ,…, ,

где — определитель системы;

— частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.

Другой вид уравнения множественной регрессии — уравнение регрессии в стандартизованном масштабе:

,

где , — стандартизованные переменные;

— стандартизованные коэффициенты регрессии.

К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (β-коэффициенты) определяются из следующей системы уравнений:

Связь коэффициентов множественной регрессии со стандартизованными коэффициентами описывается соотношением

Параметр a определяется как

Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле:

.

Для расчета частных коэффициентов эластичности применяется следующая формула:

.

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:

=.

Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:

.

Индекс множественной корреляции для уравнения в стандартизованном масштабе можно записать в виде:

=.

При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:

=,

-определитель матрицы

парных коэффициентов корреляции;

-определитель матрицы

Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора х1 при неизменном уровне других факторов, можно определить по формуле

или по рекуррентной формуле

Частные коэффициенты корреляции изменяются в пределах от -1 до 1.

Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детерминации рассматривается как квадрат индекса множественной корреляции:

.

Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле

где n — число наблюдений;

m- число факторов.

Значимость уравнения множественной регрессии в целом оценивается с помощью F — критерия Фишера:

Частный F-критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора xi частный F-критерий определится как

Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Съюдента сводится к вычислению значения

где mbi — средняя квадратическая ошибка коэффициента регрессии bi, она может быть определена по формуле:

.

При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов, их тесной линейной связанности.

Считается, что две переменные явно коллинеарны, т. е. находятся между собой в линейной зависимости, если rxixj≥0,7.

По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.

Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы rxixj (xi≠xj) были бы равны нулю. Так, для включающего три объясняющих переменные уравнения

матрица коэффициентов корреляции между факторами имела бы определитель, равный 1:

,

так как и

Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0:

.

Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и надежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Проверка мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных Ho: . Доказано, что величина имеет приближенное распределение x2 c степенями свободы. Если фактическое значение х2 превосходит табличное (критическое) , то гипотеза Ho отклоняется. Это означает, что ,недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.

Для применения МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это означает, что для каждого значения фактора xj остатки имеют одинаковую дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность.

При нарушении гомоскедастичности мы имеем неравенства

.

При малом объеме выборки для оценки гетероскедастичности может использоваться метод Гольдфельда-Квандта. Основная идея теста Гольдфельда-Квандта состоит в следующем:

1) упорядочение n элементов по мере взрастания переменной x;

2) исключение из рассмотрения С центральных наблюдений; при этом (n—C):2>p, где p-число оцениваемых параметров;

3) разделение совокупности из (n—C) наблюдений на две группы (соответственно с малыми и с большими значениями фактора х) и определение по каждой из групп уравнений регрессии;

При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять F-критерию со степенями свободы ((n—C-2p):2) для каждой остаточной суммы квадратов Чем больше величина R превышает табличное значения F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.

Уравнения множественной регрессии могут включать в качестве независимых переменных качественные признаки (например, профессия, пол, образование, климатические условия, отдельные регионы и т. д.). Чтобы вест такие переменные в регрессионную модель, их необходимо упорядочить и присвоить им те или иные значения, т. е. качественные переменные преобразовать в количественные.

Оценка значимости уравнения множественной регрессии

Построение эмпирического уравнения регрессии является начальным этапом эконометрического анализа. Первое же построенное по выборке уравнение регрессии очень редко является удовлетворительным по тем или иным характеристикам. Поэтому следующей важнейшей задачей эконометрического анализа является проверка качества уравнения регрессии. В эконометрике принята устоявшаяся схема такой проверки.

Итак, проверка статистического качества оцененного уравнения регрессии проводится по следующим направлениям:

· проверка значимости уравнения регрессии;

· проверка статистической значимости коэффициентов уравнения регрессии;

· проверка свойств данных, выполнимость которых предполагалась при оценивании уравнения (проверка выполнимости предпосылок МНК).

Проверка значимости уравнения множественной регрессии, так же как и парной регрессии, осуществляется с помощью критерия Фишера. В данном случае (в отличие от парной регрессии) выдвигается нулевая гипотеза Н₀ о том, что все коэффициенты регрессии равны нулю (b₁=0, b₂=0, … , b_m=0). Критерий Фишера определяется по следующей формуле:

где D_факт — факторная дисперсия, объясненная регрессией, на одну степень свободы; D_ост— остаточная дисперсия на одну степень свободы; R 2 — коэффициент множественной детерминации; т — число параметров при факторах х в уравнении регрессии (в парной линейной регрессии т = 1); п — число наблюдений.

Полученное значение F-критерия сравнивается с табличным при определенном уровне значимости. Если его фактическое значение больше табличного, тогда гипотеза Но о незначимости уравнения регрессии отвергается, и принимается альтернативная гипотеза о его статистической значимости.

С помощью критерия Фишера можно оценить значимость не только уравнения регрессии в целом, но и значимость дополнительного включения в модель каждого фактора. Такая оценка необходима для того, чтобы не загружать модель факторами, не оказывающими существенного влияния на результат. Кроме того, поскольку модель состоит из несколько факторов, то они могут вводиться в нее в различной последовательности, а так как между факторами существует корреляция, значимость включения в модель одного и того же фактора может различаться в зависимости от последовательности введения в нее факторов.

Для оценки значимости включения дополнительного фактора в модель рассчитывается частный критерий Фишера F_xi. Он построен на сравнении прироста факторной дисперсии, обусловленного включением в модель дополнительного фактора, с остаточной дисперсией на одну степень свободы по регрессии в целом. Следовательно, формула расчета частного F-критерия для фактора будет иметь следующий вид:

где R 2 _{yx1x2…xi…xp} — коэффициент множественной детерминации для модели с полным набором п факторов; R 2 _{yx1x2…x i-1 x i+1…xp} — коэффициент множественной детерминации для модели, не включающей фактор x_i; п — число наблюдений; т — число параметров при факторах x в уравнении регрессии.

Фактическое значение частного критерия Фишера сравнивается с табличным при уровне значимости 0,05 или 0,1 и соответствующих числах степеней свободы. Если фактическое значение F_xi превышает F_табл , то дополнительное включение фактора x_i в модель статистически оправдано, и коэффициент «чистой» регрессии b_i при факторе x_i статистически значим. Если же F_xi меньше F_табл , то дополнительное включение в модель фактора существенно не увеличивает долю объясненной вариации результата у, и, следовательно, его включение в модель не имеет смысла, коэффициент регрессии при данном факторе в этом случае статистически незначим.

С помощью частного критерия Фишера можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор x_i вводится в уравнение множественной регрессии последним, а все остальные факторы были уже включены в модель раньше.

Оценка значимости коэффициентов «чистой» регрессии b_i по критерию Стьюдента t может быть проведена и без расчета частных F-критериев. В этом случае, как и при парной регрессии, для каждого фактора применяется формула

где b_i — коэффициент «чистой» регрессии при факторе x_i ; m_bi — стандартная ошибка коэффициента регрессии b_i .

Для множественной линейной регрессии стандартная ошибка коэффициента регрессии рассчитывается по следующей формуле:

где σ_y , σ_xi — среднее квадратическое отклонение соответственно для результата у и x_i ; R 2 _{yx1x2…xi…xp} — коэффициент множественной детерминации для множественной регрессии с набором из р факторов; R 2 _{xi x1x2…x i-1 x i+1…xp} — коэффициент детерминации для зависимости фактора x_i с остальными факторами множественной регрессии.

Полученные значения t-критериев сравниваются с табличными, и на основе этого сравнения принимается или отвергается гипотеза о значимости каждого коэффициента регрессии в отдельности.

Дата добавления: 2015-10-05 ; просмотров: 5645 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

F-тест качества спецификации множественной регрессионной модели

Цель этой статьи — рассказать о роли степеней свободы в статистическом анализе, вывести формулу F-теста для отбора модели при множественной регрессии.

1. Роль степеней свободы (degree of freedom) в статистике

Имея выборочную совокупность, мы можем лишь оценивать числовые характеристики совокупности, параметры выбранной модели. Так не имеет смысла говорить о среднеквадратическом отклонении при наличии лишь одного наблюдения. Представим линейную регрессионную модель в виде:

Сколько нужно наблюдений, чтобы построить линейную регрессионную модель? В случае двух наблюдений можем получить идеальную модель (рис.1), однако есть в этом недостаток. Причина в том, что сумма квадратов ошибки (MSE) равна нулю и не можем оценить оценить неопределенность коэффициентов . Например не можем построить доверительный интервал для коэффициента наклона по формуле:

А значит не можем сказать ничего о целесообразности использования коэффициента в данной регрессионной модели. Необходимо по крайней мере 3 точки. А что же, если все три точки могут поместиться на одну линию? Такое может быть. Но при большом количестве наблюдений маловероятна идеальная линейная зависимость между зависимой и независимыми переменными (рис. 1).

Рисунок 1 — простая линейная регрессия

Количество степеней свободы — количество значений, используемых при расчете статистической характеристики, которые могут свободно изменяться. С помощью количества степеней свободы оцениваются коэффициенты модели и стандартные ошибки. Так, если имеется n наблюдений и нужно вычислить дисперсию выборки, то имеем n-1 степеней свободы.

Мы не знаем среднее генеральной совокупности, поэтому оцениваем его средним значением по выборке. Это стоит нам одну степень свободы.

Представим теперь что имеется 4 выборочных совокупностей (рис.3).

Рисунок 3

Каждая выборочная совокупность имеет свое среднее значение, определяемое по формуле . И каждое выборочное среднее может быть оценено . Для оценки мы используем 2 параметра , а значит теряем 2 степени свободы (нужно знать 2 точки). То есть количество степеней свобод Заметим, что при 2 наблюдениях получаем 0 степеней свободы, а значит не можем оценить коэффициенты модели и стандартные ошибки.

Таким образом сумма квадратов ошибок имеет (SSE, SSE — standard error of estimate) вид:

Стоит упомянуть, что в знаменателе стоит n-2, а не n-1 в связи с тем, что среднее значение оценивается по формуле . Квадратные корень формулы (4) — ошибка стандартного отклонения.

В общем случае количество степеней свободы для линейной регрессии рассчитывается по формуле:

где n — число наблюдений, k — число независимых переменных.

2. Анализ дисперсии, F-тест

При выполнении основных предположений линейной регрессии имеет место формула:

где ,

,

В случае, если имеем модель по формуле (1), то из предыдущего раздела знаем, что количество степеней свободы у SSTO равно n-1. Количество степеней свободы у SSE равно n-2. Таким образом количество степеней свободы у SSR равно 1. Только в таком случае получаем равенство .

Масштабируем SSE и SSR с учетом их степеней свободы:

Получены хи-квадрат распределения. F-статистика вычисляется по формуле:

Формула (9) используется при проверке нулевой гипотезы при альтернативной гипотезе в случае линейной регрессионной модели вида (1).

3. Выбор линейной регрессионной модели

Известно, что с увеличением количества предикторов (независимых переменных в регрессионной модели) исправленный коэффициент детерминации увеличивается. Однако с ростом количества используемых предикторов растет стоимость модели (под стоимостью подразумевается количество данных которые нужно собрать). Однако возникает вопрос: “Какие предикторы разумно использовать в регрессионной модели?”. Критерий Фишера или по-другому F-тест позволяет ответить на данный вопрос.

Определим “полную” модель: (10)

Определим “укороченную” модель: (11)

Вычисляем сумму квадратов ошибок для каждой модели:

(12)

(13)

Определяем количество степеней свобод

(14)

Нулевая гипотеза — “укороченная” модель мало отличается от “полной (удлиненной) модели”. Поэтому выбираем “укороченную” модель. Альтернативная гипотеза — “полная (удлиненная)” модель объясняет значимо большую долю дисперсии в данных по сравнению с “укороченной” моделью.

Коэффициент детерминации из формулы (6):

Из формулы (15) выразим SSE(F):

SSTO одинаково как для “укороченной”, так и для “длинной” модели. Тогда (14) примет вид:

Поделим числитель и знаменатель (14a) на SSTO, после чего прибавим и вычтем единицу в числителе.

Используя формулу (15) в конечном счете получим F-статистику, выраженную через коэффициенты детерминации.

3 Проверка значимости линейной регрессии

Данный тест очень важен в регрессионном анализе и по существу является частным случаем проверки ограничений. Рассмотрим ситуацию. У линейной регрессионной модели всего k параметров (Сейчас среди этих k параметров также учитываем ).Рассмотрим нулевую гипотеза — об одновременном равенстве нулю всех коэффициентов при предикторах регрессионной модели (то есть всего ограничений k-1). Тогда “короткая модель” имеет вид . Следовательно. Используя формулу (14.в), получим

Заключение

Показан смысл числа степеней свободы в статистическом анализе. Выведена формула F-теста в простом случае(9). Представлены шаги выбора лучшей модели. Выведена формула F-критерия Фишера и его запись через коэффициенты детерминации.

Можно посчитать F-статистику самому, а можно передать две обученные модели функции aov, реализующей ANOVA в RStudio. Для автоматического отбора лучшего набора предикторов удобна функция step.

Надеюсь вам было интересно, спасибо за внимание.

При выводе формул очень помогли некоторые главы из курса по статистике STAT 501