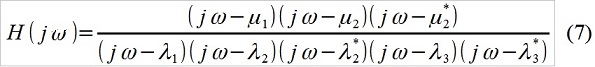Уравнение модели arma 1 2

О применении теории ARMA-процессов в инженерной практике

Ниже будет сказано несколько слов об известной вообще, но, чаще всего довольно неожиданной для инженерных работников дискретно-временной альтернативе математическим моделям в виде линейных дифференциальных уравнений, а именно, моделям авторегрессии — скользящего среднего, и весьма необычным перспективам такого моделирования, возможности которого значительно превышают то, что привыкли получать от ЛДУ.

В списке потенциальных возможностей технологии — анализ систем с недоступным для наблюдения входящим возмущением, определение резонансных свойств таких систем, спектра и самого процесса внешнего возбуждения, спектральное оценивание процессов по их коротким реализациям, моделирование поведения систем при малой частоте дискретизации по времени и т.п.

ARMA-процессы, хорошо известные экономистам (точнее, «эконометристам»), ощутимо менее — специалистам по автоматическому регулированию, и, по-моему, почти не применяются инженерами-механиками и радиоэлектронщиками, особенно «старой закалки». В статье предпринимается попытка указать некоторые возможные области применения ARMA-теории в инженерной практике.
В двух словах, упрощенно, для незнакомых с предметом, о чем, собственно, речь. Стохастическому непрерывно-временному процессу x(t) по понятным «цифровым» причинам» на практике обычно сопоставляется дискретно-временная последовательность x[i] с интервалом дискретизации Δt.
В принципе, для любого процесса x[i] возможно представление вида

где a_k и b_k – постоянные (для данной модели) коэффициенты, называемое моделью авторегрессии-скользящего среднего с порядком по авторегрессии p и по скользящему среднему q. или ARMA(p,q)-моделью, f[i] — некий «входящий» процесс, о котором чуть ниже. Часто (1) записывают в немного иной форме(6).
В общем-то, это просто цифровой фильтр, имеющий как рекурсивную AR, так и нерекурсивную MA части.
Имеет место соответствие ARMA(p,q)-моделей линейным системам (например, механическим), например, описываемым хорошо всем известным линейным дифференциальным уравнением вида

где m,c,k – масса, жесткость и демпфирование механической системы, f(t) – внешнее силовое воздействие. ARMA-аналог выглядит так:

коэффициенты модели могут быть довольно легко найдены через собственные значения λ₁ и λ₁*(для краткости рассматривается «осциллирующий» случай ) линейной системы и Δt:

где z = exp(λ₁ · Δt), λ₁ = -ε₁ +jω₁, j- мнимая единица, *- комплексное сопряжение

для справок:

Для тестовой системы было принято m=1 кг, c= 100 Н/м, k=0,75 кг/с, Δt=0,12 с.,
получена ARMA(2,1)-модель

x[i] — 0.69433x[i-1] +0.91393 x[i-2] = 0.010696·f[i-1]

(Очень краткое пояснение, как из (2) вообще получается (3). Импульсная переходная функция нашей линейной системы, т.е. отклик системы на единичный импульс:

Запись (2) в «интегральной» форме зовется «сверткой» f(t) и h(t), по смыслу предполагает рассмотрение внешнего воздействия, как последовательности элементарных импульсов. В дискретном времени записывают, ну например, так:

Сложением x[i], x[i-1] и x[i-2] с применением подобранных множителей 1, a₁ и a₂ добиваются взаимного уничтожения бесконечных «хвостов» h[i] – в правой части остаются f[i]·h[0]=f[i]·0 и f[i-1]·h[1]=f[i-1]·b₁. С точки зрения ARMA-теории, произведено преобразование бесконечномерной модели скользящего среднего МА(∞) в ARMA(2,1) (хотя некоторые скажут, что случайно получилась вообще чисто авторегрессионная модель AR(2) = ARMA(2,0)).

Замечание 1. Сведующий в цифровой обработке процессов читатель скажет, что просто так дискретизировать h(t) не очень правильно — надо ограничить функцию h(t) по частоте до 1/(2Δt) (отфильтровать). Иначе присутствует ошибка маскирования частот. На изображенных графиках АЧХ и ФЧХ нашей системы, «аналитической» и ARMA-модели, видно, почему этой ошибкой в большинстве инженерных случаев можно, скорее всего, пренебречь (рис. 1) (здесь АЧХ — в логарифмической шкале).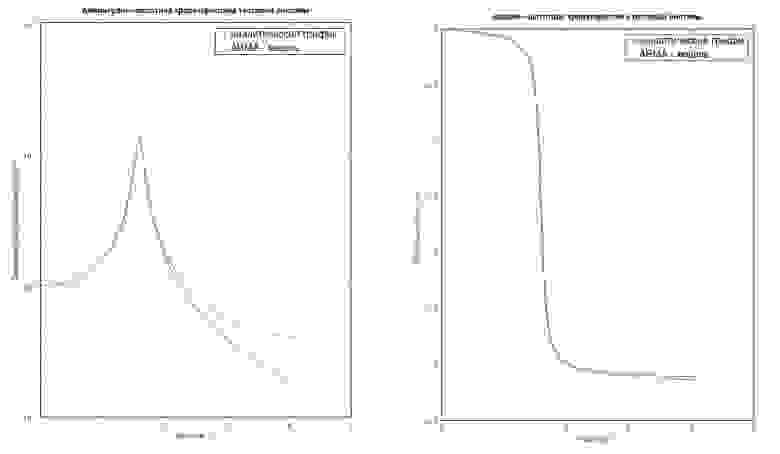

рис.1 АЧХ и ФЧХ тестовой системы.

Замечание 2. На практике порядок ARMA-модели может быть существенно больше, чем рассмотренный выше пример, вследствие, скажем, нескольких степеней свободы механической системы или сложного спектра реального внешнего воздействия.

Замечание 3. Очень важно. Существуют методы (здесь не рассмотренные — про них еще много статей можно написать), позволяющие оценить параметры ARMA-модели (а именно, порядок модели p и q и коэффициенты a_k и b_k ) только по результирующему процессу x[i], в предположении, что f[i] — гипотетический белый шум, дисперсию которого также можно оценить. В общем-то, такое оценивание и есть главная часть всей ARMA-теории. Особым совершенством пока эти методы не отличаются, но интерес представляют немалый.

Теперь о том, для чего, собственно, всё это можно (или можно было бы) применить на деле. Кроме вполне очевидного — быстрого построения «вручную» затухающих (и незатухающих) синусоид по двум первым точкам и двум коэффициентам a₁ и a₂, есть, по-моему, более серьезные приложения этих моделей в инженерной практике.

1. Ну, собственно, для симуляционного моделирования работы системы — подаем реальный внешний сигнал f[i] на вход, получаем x[i] на выходе:

ARMA-модель справляется с задачей лучше, чем конечноразностная модель, правда, заметно это только при больших интервалах дискретизации Δt. (на рис. 2, Δt = 0,12с (слева) и 0,03 с). В каких случаях есть смысл возиться с ARMA — решать вам.

рис. 2. Отклик тестовых систем на единичный импульс.

2. Для спектрального оценивания, особенно при недостаточной доступной для наблюдения длине реализации стационарного процесса. Возможно, это наиболее известное инженерное приложение ARMA-моделей. Поскольку для изучаемого процесса будет получен и некий цифровой фильтр, и дисперсия входящего в него белого шума, задача построения оценки СПМ решается очевидным образом. Действительно, можно получить внешне очень «гладкие» графики СПМ и при этом создающие впечатление высокого разрешения. Ожидаемые улучшения оценки связывают с тем, что исследователь привносит в построение оценки внешнюю информацию о природе процесса — обычно, задавая известный порядок модели.
Короче, надо знать, как примерно должна выглядеть эта СПМ. «Разведочные» исследования данной реализации с помощью классических методов могут мало что дать, в основном имеются ввиду классические (на основании БПФ) исследования похожих по природе, но ощутимо более длинных реализаций. Существует вероятность грубых ошибок.

3. Для анализа резонансных свойств системы и спектра внешнего воздействия, в случае, когда истинное внешнее воздействие недоступно для наблюдения. Как уже отмечалось, можно, зная процесс x[i], определить все коэффициенты модели a_k и b_k (и дисперсию входящего белого шума). По ним, определяя корни двух полиномов с соответствующими коэффициентами, легко уже найти p «полюсов» и q «нулей» модели ( λ_k и μ_k) и построить ее передаточную функцию — можно, наверное, даже не в ARMA-виде (здесь не приводится), а в привычном «аналитическом» виде — как мы выяснили выше (рис.1), разница невелика. Например, для p=5, q=3 (отвлекаясь пока от имеющихся, по-видимому, ограничений на соотношение p и q), как вариант, имеем:

Все очень-очень упрощенно, конечно. Исходя из известной природы исследуемого объекта (например, это полигонные испытания плавности хода автомобиля) и внешнего воздействия (микропрофиль дороги), передаточную функцию исследователь решил вот переписать, например, так:

Рис.3 Анализ спектра сигнала с выделением входящего возмущения

и прокомментировал — часть модели, связанная с λ₁, это, очевидно (с точностью до возведения в квадрат и умножения на дисперсию входящего гипотетического белого шума) «розовый» микропрофиль дороги (рис.3)(т.е. мы выделили неизвестный спектр реального входящего сигнала — выбрали вручную — вроде как «похож»), λ₂ и λ₃— резонансные свойства кузова на подвеске (возможно, продольно-угловая и вертикальная формы колебаний). Главная проблема будет, конечно, в определении параметров ARMA-модели. Для только что описанного иногда можно безо всяких ARMA по-старинке «ползать» (хоть и в электронном виде) по графику спектральной плотности и измерять ширину пиков на уровне -3 дБ и т. п., или применить курвфиттинг, иногда даже с бОльшим успехом.

3. Для линейного предсказания x[i]. По-видимому, основное приложение ARMA у «эконометристов». Из (6) видно, что, если коэффициенты модели удалось оценить методами, в общих чертах упомянутыми выше, очередное значение x[i] можно оценить с точностью до недоступного наблюдению гипотетического белого шума b₀ ·f[i], дисперсию этого белого шума оценивают вместе с коэффициентами модели. Обычно в данном случае подразумевается динамическая (в реальном времени) корректировка параметров модели. По-видимому, может быть полезно в системах активного вибро- и шумоподавления. Специалистам по ТАР виднее.

4. Для восстановления недоступного для наблюдения входящего процесса. При разделении модели на части, как было показано выше в п.3, основываясь на знаниях о природе изучаемого процесса, можно оценить отдельно спектр входящего возмущения, отдельно — осцилляторные свойства физической системы (разделить модель на части). Можно пойти дальше — сформировать фильтр (ARMA-модель, обратная части первоначальной модели), связывающий выход системы с входом, и с его помощью из результирующего процесса x[i] получить временнУю реализацию входящего возмущения. Например, попытаться восстановить неискаженный сигнал, записанный с точно неизвестными линейными искажениями аппаратурой, недоступной для отдельного исследования (скажем, полученный по телеметрии).

Исходя из своих скромных познаний, в итоге выскажу такое субъективное суждение. Применимость ARMA-технологий к инженерным задачам сильно зависит от совершенства методов оценки параметров этих моделей по результирующему сигналу, точнее, по-моему, сильно сдерживается несовершенством этих методов. Наработка опыта применения ARMA в инженерном деле, похоже, имеет смысл, в основном, именно в преддверии весьма вероятного «прорыва» в этой сфере.

Уравнение модели arma 1 2

Перед тем, как применять модель необходимо позаботиться о стационарности динамического ряда.

Ряд приводят к стационарности взятием последовательных разностей (вместо исходных 3,5,5,4,8 получится 2,0,-1,4) или преобразованием Бокса-Кокса. Стабилизировать дисперсию помогает логарифмирование.

Критерий Льюнга-Бокса — критерий для выявления автокоррелированности временных рядов.
Критерий KPSS (KPSS test) — критерий для проверки на стационарность (Hо = ряд стационарен).
Критерий Дики-Фулера — критерий для проверки на стационарность (Но = ряд нестационарен).

Лучшая модель подбирается с помощью AIC. Модель с самым низким значением информационного критерия Акаике (не несет абсолютную оценку, используется только для сравнения моделей между собой) нужно проверить на адекватность путем анализа остатков (разницы между фактическими и прогнозными значениями).

Нужно убедиться, что остатки:

• имеют низкое абсолютное значение, в них отсутствует тренд и циклы;
• распределены нормально со средним

0;

Если хотя бы что-то не так — значит модель описала не всю структуру и качество можно улучшать. Возвращаемся назад для подбора лучших параметров или преобразования исходных данных.

1. Построить график. Удалить выбросы, заменить пропущенные значения, декомпозировать ряд.

2. Обратить внимание на дисперсию, сезонность и тренд. В случае необходимости применить логарифмирование для стабилизации дисперсии или преобразование Бокса-Кокса / последовательные разности для приведения к стационарности.

3. Убедиться в стационарности ряда при помощи критерия Дики-Фуллера или теста KPSS.

4. Отобразить ACF и PACF функции, сделать предположение о модели и порядке параметров.

5. Использовать информационный критерий AIC выбора лучшей модели.
Или просто воспользоваться автотюнингом: язык программирования R > library(forecast) > auto.arima()

6. Построить ACF график остатков лучшей модели, убедиться в отсутствии корреляции остатков (тест Бокса-Кокса).

7. Если остатки выглядят как белый шум и это подтверждено тестом, то можно приступать к прогнозированию.

8. Оценить точность кросс-валидацией или прогнозом по укороченному ряду.

Некоторые динамические ряды не имеют устойчивой структуры и сильно зависят от влияния внешних факторов (например: погода, рекламный бюджет). В таких случаях целесообразно применить математическое моделирование. Подойдет простая регрессия, нейронные сеточки, случайные леса, ближайшие соседи, SVM или ансамбль из всех перечисленных (зависит от типа, распределения и объема исходных данных).

Алгоритмы будут сопоставлять весь массив входных данных (предикторов) и соответствующих значений целевой переменной (т.е. уровня продаж). Такой процесс называется «обучением». Методы машинного обучения как бы обобщают полученный опыт для ответов на новые вопросы. Гиперпараметры подгоняются так, чтобы ошибка прогнозов была минимальной.

Выбор алгоритмов их их параметров оказывают большое влияние на точность прогнозов, но определяющую роль играет набор признаков, т.е. состав переменных на которых будет будет обучаться алгоритм. При выборе признаков руководствуются физическими ограничениями, так как не все получается оцифровать и измерить (или сделать это за приемлемую цену).

Специалист из предметной области определяет набор данных, которые необходимо получить и использовать для моделирования. Если таких данных много в уже оцифрованном виде, то применяются математические методы селекции: корреляция (correlation), хи-квадрат (chi-square), мера энтропии (Informaition gain), индекс Джини (GINI index), расчет уменьшения предсказательной способности при исключении переменной, рекурсивное разбиение (Recursive partitioning), сети векторного квантования (Learning Vector Quantization) и др.

Перечислим полезные лайфхаки:

• Цикличность можно закодировать категориальным фактором (день недели или месяца) или числовой переменной, которая отражает средний уровень целевой переменной за этот период.
• Погоду, курсы валют и ставки ЦБ можно получать напрямую через API или скрапингом. Благодаря этому ваша модель будет работать без ручного обогащения новыми данными.
• Результаты прогноза по ARIMA-моделям могут быть поданы на вход другим алгоритмам для дальнейшего сокращения остатков.

Чтобы быстро прикинуть продажи в следующей неделе / месяце / году воспользуйтесь одним из наивных методов.

Для краткосрочного прогнозирования временных рядов с устойчивой структурой подходят модели класса ARIMA.

Для долгосрочного моделирования сложных и зависимых от внешних факторов процессов используйте модели машинного обучения.