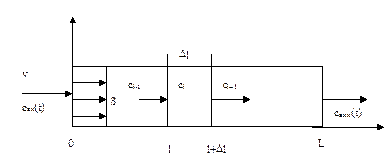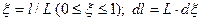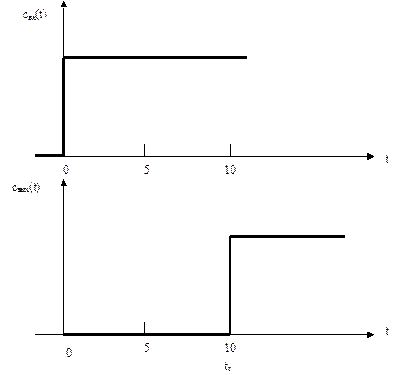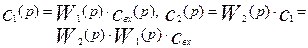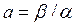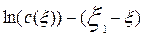Уравнение модели идеального вытеснения для температуры

Раздел 3.2 .Модель идеального вытеснения.

Рассмотрим теперь модель аппарата полного, или идеального вытеснения.

В отличие от предыдущей модели, основным постулатом этой модели является допущение о том, что в направлении потока жидкость не перемешивается, в то время как в поперечном направлении жидкость перемешана полностью. При таких допущениях жидкость в аппарате движется подобно поршню, при этом каждый последующий слой вытесняется предыдущим. Поэтому эту модель называют еще моделью поршневого потока. В англоязычной литературе эта модель называется plug flow model. Схема аппарата представлена на рис.3.2.1.

Рис.3.2.1 Схема аппарата идеального вытеснения.

– длина и площадь поперечного сечения аппарата,

— концентрация на входе и выходе из аппарата,

— объемный расход смеси на входе и выходе из аппарата.

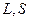
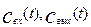
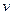
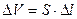
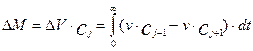
Выделим в аппарате элементарный объем и составим для него уравнение материального баланса, обозначив концентрацию в элементарном объеме через с_j, концентрацию на входе в слой через с_j-1, а концентрацию на выходе из объема через с_j+1. Накопление массы в рассматриваемом объеме будет равно интегралу от разности потоков, входящих и выходящих из рассматриваемого объема:

(3.2.1)

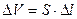
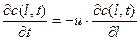
Продифференцируем обе части уравнения (3.2.1) по времени и разделим на величину рассматриваемого объема . И рассмотрев предел уравнения при Dl®0, получим уравнение модели идеального вытеснения в следующем виде:

(3.2.2)

Где 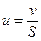— линейная скорость, м/с.

Эта модель представляет собой дифференциальное уравнение в частных производных, потому что переменная величина 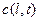изменяется в пространстве и времени. В уравнение (3.2.2) введем безразмерную пространственную координату x следующим образом:

Полученное значение производной поставим в уравнение (3.2.2) и получим математическую модель в следующем виде:

(3.2.3)

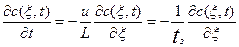
Где 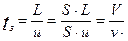— время пребывания смеси в аппарате.

Определим передаточную функцию аппарат идеального вытеснения. Для этого преобразуем уравнение (3.2.3) по Лапласу, считая x и t независимыми переменными, получим передаточную функцию модели аппарата идеального вытеснения в следующем виде:

(3.2.4)

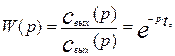
Найдем реакцию модели на импульсное возмущение, т.е.

С – кривую, используя соотношение (3.1.23):

(3.2.5)

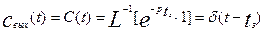
Из этой формулы видно, что выходной сигнал будет повторять входной, но сдвинут на величину t_з. Аналогично можно найти выражение для F – кривой:

(3.2.6.

На рисунках 3.2.2 и 3.2.3. показаны графики С— кривой и F – кривой:

Рис.3.2.2. Кривые отклика аппарата идеального вытеснения на импульсное возмущение, а) – изменение входной концентрации, б) изменение выходной концентрации, t_з – время пребывания смеси в аппарате

Рис.3.2.6. Кривые отклика аппарата идеального вытеснения на ступенчатое возмущение, а) – изменение входной концентрации, б) изменение выходной концентрации, t_з – время пребывания смеси в аппарате

Модель аппарата идеального вытеснения может быть использована для описания работы аппаратов, работающих по принципу вытеснения – колонные и трубчатые аппараты, теплообменники. Применение модели к описанию потоков в технологических аппаратах связывают с величиной отношения длины аппарата к его диаметру. При L/d >20 (d- диаметр аппарата) и числе Рейнольдса

Re>2300 продольное перемешивание незначительно, а турбулентное движение обеспечивает равномерно распределение концентрации по поперечному сечению аппарата. Таким образом, в этих условиях выполняются основные допущения, лежащие в основе модели идеального вытеснения.

3.3. Ячеечная модель аппарата

Ячеечную модель применяют для описания структуры потоков в аппаратах, потоки в которых не могут быть описаны моделями полного смешения или полного вытеснения. В этом случае предполагают, что весь объем аппарат может быть разделен на элементарные объемы, каждый из которых описывается моделью полного смешения. Такая модель применима также для описания потоков в каскаде последовательно соединенных аппаратов смешения. Рассмотрим движение смеси в таком каскаде аппаратов.

Рис.3.3.1 Схема ячеечной модели аппарата

v- объемный расход вещества, V_i объем ячейки (i=1,…,n) n – число ячеек,

c_i – концентрация вещества в i-м аппарате.

Составим математическое описание, описывающее структуру потоков в ячеечной модели.

Учитывая, что каждая ячейка представляет собой аппарат идеального смешения, для первой ячейки можно записать:

Продолжая эту операцию последовательно до последнего аппарата каскада, получим для выходной концентрации из каскада следующее выражение:

(3.3.1)

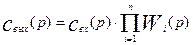
Отсюда получаем выражение для передаточной функции ячеечной модели:

(3.3.2)

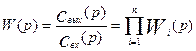
Передаточная функция n последовательно соединенных ячеек полного смешения равна произведению передаточных функций отдельных ячеек.

При условии, что V₁= V₂= V_i= V_n и v=const передаточные функции отдельных ячеек будут равны и передаточная функция, будет иметь вид:

(3.3.3)

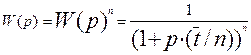
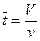
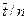
Где — среднее время пребывания смеси во всем аппарате, — среднее время пребывания в одной ячейке.

Рис.3.3.2. Кривые отклика ячеечной модели при различном числе

ячеек на ступенчатое возмущение

Раздел 3.4. Диффузионная модель

Поршневой режим движения жидкостей, рассмотренный нами при выводе уравнения модели идеального вытеснения, в реальных процессах реализуется не всегда. На самом деле в реальных процессах жидкость в различных направлениях перемещается за счет следующих явлений:

· Поперечной неравномерности профиля скорости.

· Пристеночных эффектов, каналообразования.

· Переноса за счет молекулярной диффузии.

Будем считать, что все отклонения режима движения от поршневого режима, могут быть сведены к переносу в обратном направлении, за счет влияния конвективной диффузии, или осевой дисперсии.

На рис 3.4.1. приведена схема потоков в таком аппарате:

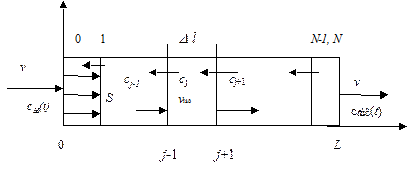Рис.3.4.1. Схема потоков в аппарате, описываемом диффузионной моделью.

V=S×L – объем аппарата, S=p×d 2 /4 – площадь поперечного сечения, L – длина аппарата.

Стрелками в обратном направлении обозначен перенос вещества в обратном направлении за счет конвективной диффузии или продольной дисперсии.

Составим уравнение материального баланса для аппарата с приведенной структурой потоков.

Поток вещества за счет турбулентной диффузии описывается уравнением, подобным уравнению диффузии Фика:

(3.4.1)

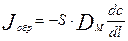
Где J_обр— поток вещества в обратном направлении.

D_M – коэффициент обратного переноса массы за счет турбулентной диффузии.

Составим уравнение материального баланса для элементарного объема аппарата, ограниченного сечениями j-1 и j+1, расположенными на расстоянии Dl.

Приход вещества в рассматриваемый объем складывается из прихода за счет конвективного переноса и за счет обратного потока из предшествующего объема аппарата:

(3.4.2)

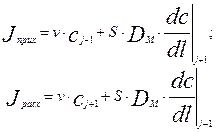
Накопление массы в рассматриваемом элементарном объеме будет равно интегралу от разности входящего и выходящего потоков в объем:

(3.4.3)

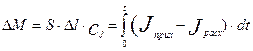
Перейдем теперь от накопления массы в объеме к изменению концентрации. Для этого разделим обе части уравнения на величину элементарного объема DV=S×Dl и продифференцируем обе части уравнения по времени. С учетом того, что производная от интеграла по аргументу равна подинтегральному выражению и уравнения (3.4.2) для потоков прихода и расхода вещества, уравнение принимает следующий вид:

(3.4.4)

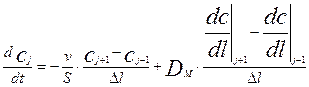
Рассмотрим пределы слагаемых правой части уравнения (3.4.4) при Dl®0.

(3.4.5)

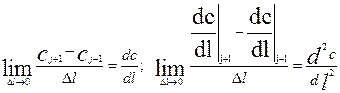
Подставив выражения пределов из (3.4.5) в (3.4.4) получим окончательно уравнение диффузионной модели в следующем виде:

(3.4.6)

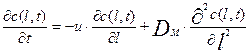
Уравнение записано как дифференциальное уравнение в частных производных, так как концентрация является функцией двух независимых переменных с(l,t). В дальнейшем мы не будем это писать для сокращения записей но будем постоянно иметь в виду, что с=с(l,t).

Приведем уравнение к безразмерному виду с помощью следующих подстановок:

x=l/L, где l – текущая длина, а L – полная длина аппарата. Тогда Ldx=dl и dl 2 =L 2 dx 2 . С использованием этих подстановок уравнение диффузионной модели может быть преобразовано к следующему виду:

(3.4.7)

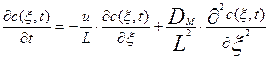
Умножим обе части уравнения (3.4.7) на величину

— среднее время пребывания в аппарате. В итоге получим:

(3.4.8)

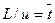
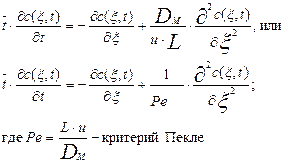
Рассмотрим предельное выражение уравнения диффузионной модели при Ре® ¥. При Ре® ¥1/Ре®0. Таким образом, уравнение диффузионной модели превращается в следующее уравнение:

,

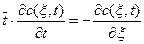
которое, является уравнением модели идеального вытеснения.

Для решения уравнения диффузионной модели преобразуем его по Лапласу по переменной t. В итоге получим:

(3.4.9)

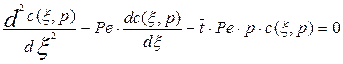
Уравнение (3.4.9) представляет собой однородное обыкновенное дифференциальное уравнение с постоянными коэффициентами.

Его решение имеет вид:

((3.4.10)

Где K₁ и K₂ корни характеристического уравнения, соответствующего дифференциальному уравнению (3.4.9).

. Характеристическое уравнение для уравнения (3.4.9) будет иметь вид:

(3.4.11

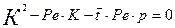
Найдем корни этого характеристического уравнения:

(3.4.12

Обозначим первое слагаемое в уравнении (3.4.12 через a, а второе через b.

Корни характеристического уравнения можно записать в следующем виде:

, .

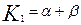
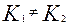
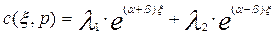
Тогда общее решение уравнения (3.4.9) для случая когда (корни различные и действительные) можно записать в виде:

(3.4.13

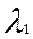
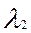
где — и – постоянные интегрирования, определяемые из граничных условий.

Если (корни равные и действительные)

(3.4.14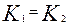

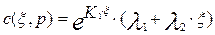
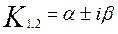
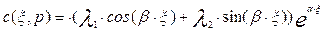
Если корни комплексные — a- действительная часть, i×b -мнимая часть, то решение имеет вид:

(3.4.15

Постоянные интегрирования можно определить из граничных условий, выражающих закон сохранения массы на входе и выходе из аппарата, указанной на схеме рис.3.4.1. Приход массы в эту ячейку складывается из прихода с входным потоком и прихода за счет обратного диффузионного потока. Расход складывается из конвективного уноса массы в последующие объемы аппарата. Из равнения материального баланса на входе в аппарат следует:

(3.4.15

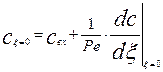
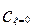
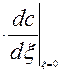
Где и — концентрация и ее производная по безразмерной длине на воде в аппарат,

— концентрация трассера во входном потоке.

И уравнения (3.4.15) следует, что концентрация вещества во входном сечении аппарата не равна концентрации во входном потоке, Она изменяется скачкообразно за счет действия обратного перемешивания.

Из уравнения материального баланса в выходном сечении аппарата определяем 2-е граничное условие:

(3.4.16).

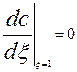
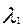
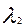
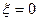
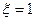
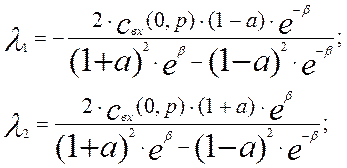
Используя граничные условия (3.4.15) и (3.4.16) можно определить постоянные интегрирования и в уравнении (3.4.13). Для этого нужно определить значение концентрации и ее производной по длине во входном сечении при , , а также значение производной при . Подставив эти значения в уравнения (3.4.15) и (3.4.16), определим значения постоянных интегрирования

(3.4.17)

где

Подставив найденные выражения для постоянных интегрирования в уравнение (3.4.13), найдем уравнение для зависимости концентрации от длины и переменной Лапласа в следующем виде:

(3.4.18)

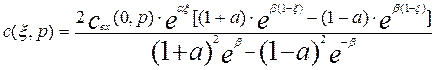
найдем передаточную функцию аппарата с конечными размерами. Для этого вычислим значение выходной концентрации, положив в уравнении (3.4.19) x=1.

В итоге получим:

(3.4.19)

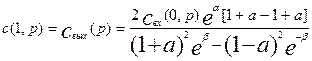
откуда найдем передаточную функцию:

(3.4.20)

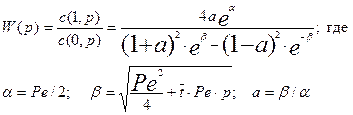
Критерий Пекле и коэффициент продольной диффузии , являющиеся параметрами диффузионной модели определяют экспериментально с использованием экспериментов с трассерами. Методы определения параметров модели по экспериментальным данным мы рассмотрим ниже.

Рассмотрим решение уравнения диффузионной модели для аппарата бесконечно больших размеров. В таком аппарате возмущения не доходят до его границ. Поэтому можно считать, что концентрация на входе в аппарат равна концентрации во входном потоке, а концентрация на выходе равна нулю, при . Для этого случая граничные условия будут иметь вид:

, так как . Для этих значений граничных условий решение уравнения диффузионной модели будет иметь следующий вид:

(3.4.21)

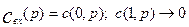
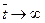
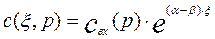
Концентрация на выходе из аппарата будет равна:

(3.4.22)

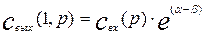
Откуда передаточная функция аппарата бесконечно больших размеров будет равна:

(3.4.23)

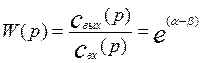
Стационарный метод определения критерия Пекле.

Суть этого метода заключается в следующем. На некотором расстоянии от начала аппарата 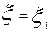вводится трассер с постоянной скоростью.

Когда процесс станет установившимся, т.е. ,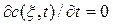

будет наблюдаться некоторое стационарное распределение концентрации трассера. Это распределение будет описываться стационарным уравнением диффузионной модели, которое получается из уравнения (4.3.8):

(3.4.24

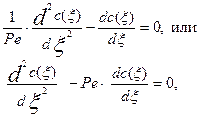
Решением уравнения (3.4.24) будет уравнение вида:

(3.4.26)

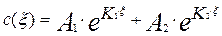
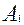
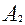
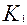
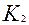
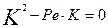
где и постоянные интегрирования, которые находятся из граничных условий, соответствующих условиям проведения эксперимента, а и корни характеристического уравнения соответствующего исходному дифференциальному уравнению (3.4.25). Характеристическое уравнение будет иметь вид:

.

Корни могут быть определены следующим образом:

.

.

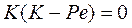
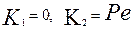
С учетом этого уравнение (3.4.26) примет вид:

(3.4.27)

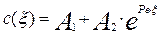
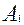
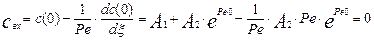
Для нахождения воспользуемся первым граничным условием:

,

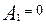
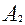
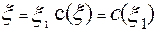
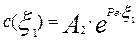
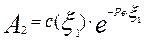
Откуда следует, что , так как концентрация трассера на входе в аппарат равна нулю. Для нахождения воспользуемся вторым граничным условием, а именно: при

,

,

.

Подставляя найденные значения постоянных интегрирования в (3.4.27), получим уравнение для описания стационарного профиля концентрации трассера:

(3.4.28)

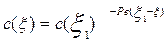
Логарифмируя выражение (3.4.28), получим следующее уравнение:

(3.4.29)

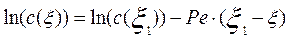
Это уравнение представляет собой уравнение прямой в координатах

Найдя из графика тангенс угла наклона прямой линии a, можно рассчитать критерий Пекле по формуле

,

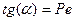
зная критерий Пекле, можно рассчитать коэффициент обратной диффузии по формуле:

(3.4.30)

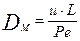
Таким образом, для определения критерия Ре, необходимо определить ряд концентраций трассера по длине аппарата, отложить их в координатах

,

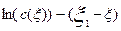
и из полученной прямой определить критерий Пекле из тангенса угла наклона полученной прямой. Одновременно определяется адекватность применения диффузионной модели для описания движения потока в данном аппарате.

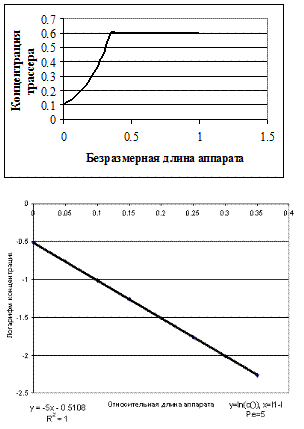Рис.3.11 . Определение числа Пекле методом стационарного ввода трассера.

3.5.Комбинированные модели

Не все реальные процессы могут быть описаны с помощью рассмотренных моделей. К таким процессам относятся процессы, включающим байпасные и циркуляционные потоки, а также застойные зоны. При построении комбинированных моделей принимают, что аппарат состоит из отдельных зон, соединенных между собой последовательно или параллельно, причем каждая из зон может быть описана одной из рассмотренных выше идеальных моделей. Следует отметить, что увеличением количества зон можно описать процесс любой сложности, однако полученное при этом математическое описание получается достаточно сложным для анализа. Рассмотрим несколько типов комбинированных моделей.

3.5.1.Модель с застойной зоной

Застойная зона – это участок в объеме аппарата, в котором происходит слабое перемешивание, и обмен этого участка с остальным объемом аппарат затруднен. В соответствии с этим допущением весь объем аппарата может быть разделен на две части – хорошо перемешиваемый объем V_o и объем застойной зоны V_зз.

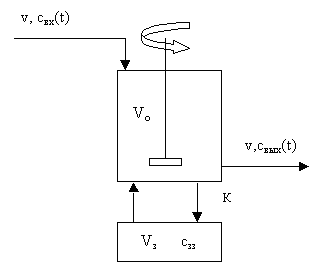Рис.3.5.1 Схема аппарата с застойной зоной.

– объем части аппарата идеального смешения,

– объем застойной зоны, – концентрация в застойной зоне

— объемный расход смеси через аппарат, – коэффициент обмена между застойной и перемешиваемой частями аппарата, — концентрация на входе и выходе из аппарата

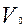
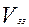
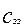
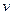
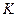
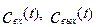
Для получения математической модели составим обобщенное уравнение материального баланса для каждой зоны.

· Для хорошо перемешиваемой зоны:

(3.5.1)

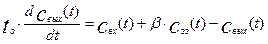
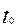
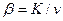
где – время пребывания в хорошо перемешиваемой зоне, — коэффициент, учитывающий интенсивность обмена проточной части с застойной зоной.

· Для застойной зоны

(3.5.2)

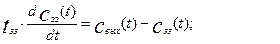
где 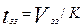– среднее время пребывания вещества в объеме застойной зоны..

Преобразуем уравнения (3.5.1) и (3.5.2) по Лапласу:

;

;

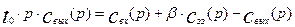
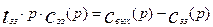
Из второго уравнения системы (3.5.3) найдем :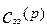

и подставим его в первое уравнение системы:

(3.5.4)

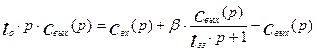
Из уравнения (3.5.4) найдем передаточную функцию модели с застойной зоной в следующем виде

(3.5.5)

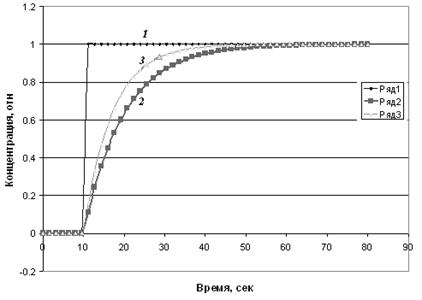
Полученная передаточная функция соответствует модели идеального смешения с застойной зоной. На рис.3.5.2 показаны кривые разгона модели идеального перемешивания и модели с застойной зоной при равных общих объемах аппаратов. Для аппарата с застойной зоной характерно более быстрое изменение в начальные моменты времени и более медленное изменение в конце процесса. Появляется затянутый «хвост» кривой, соответствующий медленному вымыванию трассера из застойной зоны.

Рис.3.5.2. Кривые разгона аппарата идеального перемешивания (Ряд-2) и аппарата с застойной зоной (Ряд 3) при ступенчатом возмущении на входе (Ряд 1)

3.5.2.Модель с байпасным потоком.

Модель с байпасным потоком описывает ситуацию, когда часть входного потока проскакивает на выход не смешиваясь с содержимым аппарата.

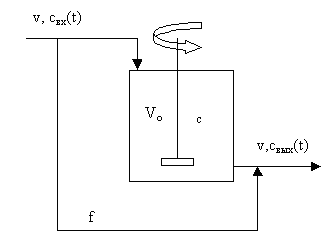На рис. 3.5.3. приведена схема аппарата с байпасированием части потока.

Рис.3.5.3. Схема аппарата с байпасированием части потока.

Здесь V_o – объем аппарата с интенсивным смешением, c- концентрация в объеме зоны смешения, f-доля байпасного потока.

Концентрация в аппарате описывается дифференциальным уравнением:

(3.5.6)

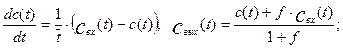
Откуда передаточная функция аппарат с байпасированием потока будет иметь вид:

(3.5.7)

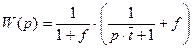
Где 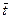среднее время пребывания реакционной смеси в проточной части аппарата.

f— доля байпасной части потока

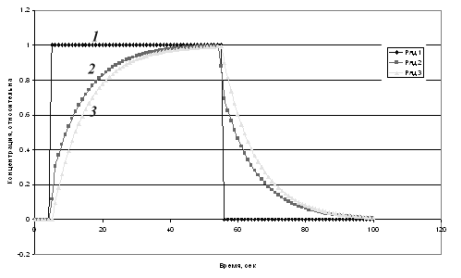
Рис.3.5.4.Кривые отклика аппарата идеального перемешивания и аппарата с байпасным потоком на ступенчатое импульсное возмущение.

1- входной ступенчатый импульс

2- выходная кривая для аппарата с байпасным потоком

3- выходная кривая для аппарата идеального перемешивания

3.5.3.Последовательное соединение ячеек идеального вытеснения и идеального смешения.

На рис.3.5.4 представлена схема аппарата в виде последовательного соединения зон идеального вытеснения и зон идеального смешения.

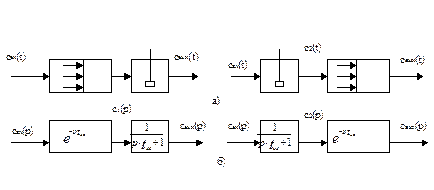Рис. 3.5.4. Схема комбинированной модели аппарата с последовательным соединением зоны идеального вытеснения и зоны идеального смешения при различной последовательности их расположения.

а) схема расположения аппаратов; б)- структурная схемы.

Из рисунка видно, что передаточная функция последовательно включенных звеньев равна произведению передаточных функций отдельных звеньев. Таким образом, общая передаточная функция комбинированной модели будет иметь следующий вид:

(3.5.8)

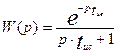
Математически передаточная функция будет одинакова, независимо от последовательности включения звеньев. При этом кривые отклика будут иметь одинаковый вид при замере выходной концентрации на выходе из всех звеньев. Для различия порядка включения звеньев нужно замерять концентрации в промежуточных точках соединения звеньев. На рис. 3.5.5 показаны кривые разгона этой модели, при различной последовательности их расположения. Следовательно, одинаковые кривые отклика аппаратов на ступенчатый сигнал ( или другого типа воздействие) – это еще не полная информация о гидродинамике потока.

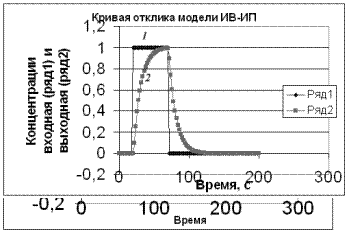б)

Рис.3.5.5. Кривые отклика комбинированной модели идеального перемешивания (ИП) и идеального вытеснения (ИВ) при раличной последовательности их соединения

3.5.4.Гидродинамические модели многофазных

потоков.

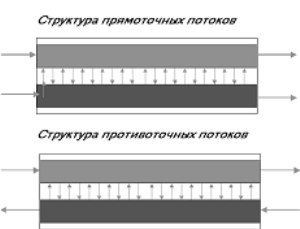Для описания процессов в технологических аппаратах, через которые протекают многофазные потоки реагирующих компонентов применяют обычно разработанные гидродинамические модели однофазных потоков для каждой из фаз. Эти модели дополняются источниковыми членами, учитывающими массо- и теплообмен между фазами, а также источниковыми членами, учитывающими превращение веществ за счет химических реакций и тепловыделение ( или теплопоглощение) за счет химических превращений и фазовых переходов. Используемая структура потоков в многофазных реакторах и технологических объектах показана на рисунке:

Рис.3.5.3.Структура многофазных потоков

Используем диффузионную гидродинамическую модель для описания процессов в аппаратах с многофазными потоками, так как ранее было показано, что диффузионная модель содержит в себе, в качестве предельных случаев и модель идеального вытеснения (при D®0) и модель идеального перемешивания (при D® ¥).

Ниже приведены уравнения, описывающие процессы переноса тепла и вещества в пределах каждой из фаз потоков, с учетом тепло — массообмена между фазами:

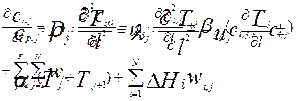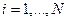
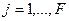
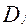
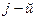
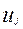
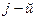
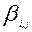
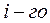
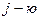
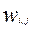
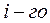
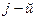
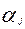
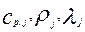
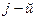
где – число реагирующих компонентов компонентов.

– число фаз, образующих потоки регентов.

— коэффициент диффузионного перемешивания в фазе

-линейная скорость движения потока фазы

— коэффициент массопередачи в фазу

– скорость реакции компонента в фазе

– коэффициент теплопередачи между фазами

– теплоемкость, плотность и теплопроводность фазы.

Аналогичные уравнения можно получить для многофазных систем и при использовании других моделей гидродинамики, при этом можно использовать различные модели для каждой из фаз.

3.6.Методы определения параметров моделей

структуры потоков.

Уравнение модели идеального вытеснения для температуры

Для поверочного расчета имеем

[ Второй корень уравнения (18) отрицателен и потому лишен физического смысла].

Для проектного расчета можно записать

О реалистичности моделей идеальных потоков .
Идеальные по­токи – сильно упрощенные модели. Законен вопрос: насколько можно считать их соответствующими каким-либо реальным объек­там. Оказывается, такое соответствие существует достаточно часто .

Так, к идеальному вытеснению близок поток жидкости или га­за через достаточно длинный аппарат, заполненный слоем зерни­стого материала (насадочная колонна, реактор с неподвижным слоем катализатора, шахтная печь). Зернистый слой интенсивно выравнивает поток. В меньшей степени можно применить эту мо­дель к потоку в пустой трубе, особенно в ламинарном режиме .

Близко к идеальному смешению течение жидкости через аппа­рат с мешалкой, через барботажный слой. В том же барботажном слое течение газа плохо описывается данной моделью, но часто нам нужно описать именно движение жидкости .

В практических расчетах процессов мы во многих случаях удовольствуемся моделями идеальных потоков. Так, рассчитывая время контакта (время протекания реакции) в каталитическом ре­акторе или скорость газа в насадочной колонне, мы не принимаем во внимание реальную неравномерность, размытость этих величин, т. е. ведем расчет в приближении идеального вытеснения. С дру­гой стороны, рассчитывая выпарной аппарат с принудительной циркуляцией, мы, как правило, считаем концентрацию упаривае­мого раствора одной и той же во всем объеме, что соответствует идеальному смешению .

Часто такое пренебрежение неидеальностью потока действи­тельно допустимо, и тогда, разумеется, применять более сложные модели нецелесообразно. Но есть и случаи, когда недопустимо грубо пользоваться приближением идеальных потоков. Поэтому очень важно в каждом конкретном случае оценить возможную ошибку идеализации, обусловливающую неадекватность мо­дели .

Сопоставление идеальных потоков проведем таким образом, как будто имеем дело с реальными аппаратами (можно иметь в виду случаи, когда данное описание достаточно точно). Вначале сопоставим особенности описания, а затем – протекание в этих по­токах различных процессов .

Каждый из идеальных потоков отличает предельная равномер­ность. В идеальном вытеснении это равномерность скоростей и времени пребывания, в идеальном смешении – равномерность кон­центраций и температуры по объему .

Стационарный процесс в потоке идеального вытеснения описы­вается системой дифференциальных уравнений типа (1). Для идеального смешения этот случай описывается уравнениями (9) или (11) – конечными уравнениями, не содержащими оператора дифференцирования. Лишь в нестационарном случае в описании появляются производные – см. уравнения (10), (12). Объясняется это тем, что в идеальном смешении равны нулю производные по координатам – градиенты концентраций и температуры .

В связи с этим процесс в данном потоке можно описывать так, будто он целиком происходит в одной точке (от точки к точке ничто не меняется). И в нестационарном процессе аппарат идеаль­ного смешения ведет себя «как точка» – все изменения происхо­дят во всем объеме одновременно. Такой объект называют объ­ектом с сосредоточенными параметрами. Аппарат идеального вытеснения – объект с распре­деленными параметрами: в нем параметры процесса ме­няются от точки к точке. Правда, это простейший из таких объек­тов – одномерный, поскольку рассматриваются изменения лишь в продольном направлении, а поперек потока все считается выровненным. Тем не менее, описание идеального смешения еще проще. Эта простота привлекательна с точки зрения математичес­кой обработки модели; поэтому, как увидим ниже, ряд более сложных моделей строится на основе модели смешения .

Посмотрим теперь, как равномерность или неравномерность распределения параметров влияет на ход химической реакции. Рассмотрение будем проводить на примере простейшей реакции :

Рис . 5 . График изменения концентрации реагента по длине

аппарата: 1 – поток идеального вытеснения; 2 – поток идеального смешения .

Многие выводы из нашего рассмотрения будут верны для боль­шинства формально простых реакций, обратимых реакций, а так­же для процессов массо- и теплообмена, формальное описание ко­торых аналогично описанию обратимой реакции 1-го порядка .

Вначале проведем качественный анализ. Равномерность време­ни пребывания в идеальном вытеснении способствует глубокому протеканию реакции, так что преимущество сле­дует отдать потоку вытеснения .

Как влияет на процесс равномерность концентраций в потоке смешения ? Построим график изменения концентрации реагента А по длине l аппарата идеального вытеснения , либо идеального сме­шения ( рис. 5 ). На графике l =0 – вход в аппарат ; l = L – вы­ход. Значения l l > L соответствуют трубам, подводящим жидкость к аппарату и отводящим прореагировавшую смесь. Бу­дем считать заданными исходную концентрацию с ао и конечную с Ак .

В идеальном вытеснении легко связать пройденный частицей путь с временем протекания реакции в этой частице

где w — линейная скорость .

Уравнение ( 2 ) соответственно получит вид

( см. экспоненту на рисунке ).

В аппарате смешения картина совершенно иная. На входе про­исходит скачок концентрации А до значения, которое дальше со­храняется вплоть до выхода. По всей длине аппарата с а = с а к .

Если теперь рассмотреть одно и то же произвольное попереч­ное сечение обоих аппаратов, то, очевидно, значение с а в аппара­те вытеснения окажется больше соответствующего значения в ап­парате смешения. Скорость реакции, пропорциональная с а , во всех сечениях аппарата, кроме последнего (на выходе), также бу­дет большей в аппарате вытеснения, чем в аппарате смешения. Получить картину, показанную на рис. 5 (одинаковые началь­ные и одинаковые конечные с а ), можно только, если объем аппа­рата смешения больше объема аппарата вытеснения .

Отсюда можно сделать два вывода: 1) аппарат вытеснения обеспечивает большую эффективность процесса; 2) на кинетику реакции влияет не только химизм, но и характер потока .

Таким образом, и анализ распределения времени пребывания, и анализ распределения концентрации приводят к выводу о боль­шей эффективности потока вытеснения. Правда, судить об эффек­тивности только по скорости протекания реакции нельзя. Конст­рукции аппаратов, близких к идеальному вытеснению и к идеаль­ному смешению, различны. В частности, интенсивное перемешива­ние способствует массо- и теплообмену. Часто процессы, для ко­торых важен перенос тепла и вещества, проще оформить в аппа­рате с перемешиванием, и тогда возникает проблема: чем жерт­вовать – простотой конструктивного оформления или отсутствием продольного перемешивания .

Пример 3 . Проблема выбора типа аппарата .

Проектируется аппаратурное оформление сильно экзотермической каталити­ческой реакции. Можно поместить неподвижный катализатор в трубки – поток будет близок к идеальному вытеснению. Но для обеспечения отвода тепла труб­ки придется делать узкими, и следовательно, при данном обгеме катализатора их будет много. Промышленные реакторы этого типа содержат по нескольку тысяч трубок – это сложные и дорогие аппараты .

Можно применить псевдоожиженный слой катализатора – отвод тепла уп­ростится, хотя вследствие влияния продольного перемешивания придется брать больший объем аппарата и большее количество катализатора .

Решение вопроса об эффективности того или иного потока должно, разумеется, базироваться на количественных оценках, к которым мы и перейдем. По-прежнему будем анализировать реак­цию (21) .

Можно сопоставить выражения (3) и (16) . Задав ряд значений , рассчитаем при каждом из них степень превращения в потоках идеального вытеснения х выт и идеального смешения х см :

При малых значениях , соответствующих случаям малого объема аппарата или медленной реакции , разница не очень вели­ка (

6% при = 0,5 ). При росте разница может оказаться очень большой .

Еще яснее видно различие при сопоставлении результатов про­ектного расчета, когда задается требуемая величина х и по фор­мулам (4) и (17) совместно с (1) рассчитываются потреб­ные объемы аппаратов . Приведем значения отношения этих объе­мов V см / V выт при различных требуемых х :

Результаты последнего сопоставления очень показательны. Ес­ли требуется невысокая степень превращения (менее 0,9), то проигрыш вследствие перехода от идеального вытеснения к иде­альному смешению не слишком велик. Оценивая эффективность, нужно учитывать и иные факторы. Но если требуется степень превращения 99% или выше, различие столь велико (в десятки или даже сотни раз), что ясно: необходимо применять аппараты, максимально близкие к идеальному вытеснению :

Пример 4 . Проблема выбора типа аппарата .

Продолжим рассмотрение, начатое в примере 3. То обстоятельство, что при небольших степенях превращения проигрыш вследствие продольного смеше­ния невелик, позволяет решить две задачи (отвод тепла и глубокое превращение реагентов) порознь, в разных аппаратах .

Вначале можно поставить аппарат с интенсивным перемешиванием, получая в нем степень превращения 80–90% и соответственно отводя 80–90% всего вы­деляющегося тепла. А затем направить реагирующую массу в аппарат вытесне­ния, где превращение доходит до высокой степени. В этом аппарате отвод тепла упрощен, так как основная часть его уже отведена на предыдущей ступени .

Вывод о том, что в аппарате вытеснения глубина превращения выше, чем в аппарате смешения, и что преимущество этого потока возрастает по мере роста требуемой степени превращения, верен для изотермических необратимых и обратимых реакций любого порядка (кроме нулевого), а также для большинства тепло- и массообменных процессов. Можно показать, что по глубине протека­ния процесса поток идеального вытеснения теоретически наи­лучший для всех процессов, скорость которых падает по мере протекания процесса .

Иногда делают обратный вывод, считая, что если один идеальный поток – Наилучший, то второй (смешение ) – наихудший. Но это неверно. Существуют потоки, много худшие, чем идеальное смешение – прежде всего это потоки c большими застойными зонами или мощными короткими байпасами .

Нужно также иметь в виду, что существует ряд процессов, в которых закон изменения скорости по ходу процесса иной. Внача­ле скорость мала, постепенно она нарастает и затем, достигнув максимума, начинает спадать (рис. 6). Объясняется это тем, что в процессе вырабатывается какая-либо субстанция (вещество или энергия), ускоряющая процесс. Вначале этой субстанции ма­ло, процесс медленный. По мере протекания он самоускоряется до максимума, после которого скорость падает вследствие нехватки исходного вещества. Отметим 4 группы таких процессов .

Автокаталитические реакции , в которых один из продуктов ре­акции ускоряет процесс. Пока этого продукта мало, реакция мед­ленная. Накопление катализатора ведет к ускорению реакции до тех пор, пока в конце процесса убыль исходных веществ не обус­ловит снижение скорости .

Биохимические реакции , вызываемые микроорганизмами – бро­жение, ферментация. На начальной стадии процесса его скорость возрастает в связи с интенсивным размножением микроорганизмов. В конце процесс замедляется вследствие недостатка пищи .

Экзотермические реакции , в которых вначале за счет тепла ре­акции происходит разогрев, ведущий к росту скорости .

Процессы кристаллизации . В начальной стадии процесса ско­рость растет благодаря увеличению числа зародышей кристалли­зации. Затем образование новых зародышей прекращается, и ско­рость снижается вследствие уменьшения пересыщения .

Если процесс такого типа проводить в аппарате вытеснения, то на начальном отрезке аппарата скорость мала, и эта его часть используется неэффективно. В таком случае более эффективным может оказаться аппарат смешения: в нем просто поддерживать высокую концентрацию катализатора, микроорганизмов, зароды­шей кристаллизации или высокую температуру. Причем эта опти­мальная концентрация или температура поддерживается во всем объеме аппарата .

После того, как процесс пройдет через максимум скорости, он будет идти как процесс с падающей скоростью. Поэтому на этом этапе (на «хвосте» процесса) смесь выгодно вывести из аппарата смешения и направить в аппарат вытеснения .

В ряде подобных случаев процесс можно проводить и в аппа­рате вытеснения, но тогда для ускорения процесса на начальной стадии осуществляют циркуляцию: часть потока, выходящего из аппарата, возвращают на его вход (рис. 7). С этим циркуля­ционным потоком в начальный участок аппарата вносится «за­травка», ускоряющая процесс. Можно отметить, что циркуляция вообще влияет аналогично продольному смешению .

Сложные реакции в идеальных аппаратах .
При проведении сложных реакций с побочными стадиями обычно главной задачей является достижение высокой селективности. Зачастую ради это­го жертвуют степенью превращения: недопревратившиеся реаген­ты можно отделить от вышедшей из аппарата смеси и вернуть в начало процесса. В результате стоимость переработки возрастает на величину стоимости процесса разделения. Низкая же селектив­ность означает, что, во-первых, часть исходных веществ затрачи­вается бесполезно (переходит в ненужные побочные продукты). Во-вторых, эти побочные продукты также приходится отделять :

затраты на разделение могут быть даже большими, чем при низ­кой степени превращения. И в-третьих, с побочными продуктами после их отделения нужно что-то делать. Просто выбросить их, как правило, нельзя: загрязнение окружающей среды в наше вре­мя становится одной из тяжелейших проблем, стоящих перед человечеством. Обезвреживание или уничтожение побочных продук­тов ложится тяжелым грузом на экономику процесса .

Рис. 6. График изменения во времени скорости процесса с самоускорением .

Рис. 7. Схема аппарата с циркуляцией .

Характер влияния потока на сложные реакции отличается большим разнообразием. Рассмотрим два простых случая: реак­цию с последовательной побочной стадией и реакцию с парал­лельной побочной стадией .

Рис.8. График изменения концентраций во времени для последовательной реакции: 1 – исходное вещество А; 2 – целевой продукт В ;

3 – побочный продукт С .

На рис. 8 показано изменение концентрации по времени протекания последовательной реакции :

Если В – целевой продукт, а С – отброс, то концентрация целево­го продукта вначале растет, проходит максимум и далее падает. Можно показать, что селективность этой реакции падает с самого начала . Оптимальными будут условия, когда ев не дошло до мак­симума: хотя при этом степень превращения А мала, но зато ве­лика селективность. Если реакция проходит в аппарате идеального вытеснения, то состав смеси будет соответствовать оп­ределенному значению t (см. рис. 8) .

В потоке смешения положение будет иным. Наряду с частица­ми, выходящими из аппарата через малое время после входа, най­дутся и такие, которые задерживаются в нем намного дольше среднего. Как видно из рис. 8, в этих частицах практически весь реагент А превратится в побочный продукт С. Этот отброс будет загрязнять выходящую смесь, снижая селективность .

Пример 5 . Расчет селективности последовательной реакции. Примем в реакции (23) условие k 1 = k 2 = k . Тогда для идеального вытесне­ния система уравнений кинетики будет иметь вид (для концентрации С приведе­но уравнение стехиометрического баланса):

откуда для степени превращения А и селективности легко получить уравнения

Для идеального смешения уравнения материального баланса по А и по В будут иметь следующий вид (для С верно записанное выше стехиометрическое соотношение ):

Легко получить решение этих уравнений

Сопоставление формул (24) – (27) показывает, что при равных значениях х величина о в аппарате идеального вытеснения окажется заметно выше, чем в аппарате идеального смешения (рис. 9 ).

Рис . 9 . Зависимость селективности от степени превращения

реагента : 1 – идеальное вытеснение ; 2 – идеальное смешение .

Если бы целевым продуктом было вещество С , то выход его был (при заданном ) много больше в потоке вытеснения, чем в потоке смешения. И в этом случае поток вытеснения был бы предпочтительнее.

Для параллельной реакции (В – целевой продукт )

влияние структуры потока на селективность зависит от соотноше­ния порядков основной и побочной стадии .

Если обе стадии – одинакового порядка , то соотношение ско­ростей образования обоих продуктов зависит только от соотноше­ния констант скорости

В этом случае селективность не меняется по ходу реакции (если не меняется температура) и не зависит от типа потока .

Теперь пусть первая стадия — первого порядка, а вторая – второго . Рассчитаем отношение r B к r C

Это отношение , а стало быть , и селективность тем больше , чем меньше c A .

Обратимся к рис. 5. При заданной степени превращения А его концентрация в любом поперечном сечении аппарата смеше­ния будет ниже, чем в соответствующем сечении аппарата вытес­нения. Значит, в этом случае процесс в аппарате идеального сме­шения будет проходить хотя и медленнее, но зато с существенно большей селективностью, т. е. именно аппарат смешения окажется наилучшим .

Нетрудно понять, что если целевая реакция – второго поряд­ка, а побочная – первого, то все преимущества будут на стороне идеального вытеснения .

Рассмотрим процессы полимеризации в потоке. Реак­ция полимеризации состоит из чрезвычайно большого числа по­следовательных стадий присоединения молекул мономера к расту­щей цепи. В этом случае нельзя говорить о целевом веществе: про­дукт представляет собой смесь макромолекул разной длины. Эту смесь можно охарактеризовать функцией распределения степени полимеризации (или длины цепей). Свойства полимера существен­но зависят как от средней длины цепей (математического ожида­ния), так и от дисперсии этой величины. В боль­шинстве случаев стремятся получить молекулярно одно­родный полимер: продукт с малой дисперсией степени полимери­зации .

Теоретические исследования и математическое моделирование показали, что влияние структуры потока на распределение степени полимеризации зависит от особенностей кинетики поли­меризации. Можно выделить два крайних случая .

Рис . 10 . График интегральных функций распределения степени

полимеризации N полистирола .

Медленный рост цепей , который продолжается на протяжении всего времени пребывания и прерывается на выходе из аппарата. Тогда длина цепи в основном определяется временем пребывания»

и наибольшая однородность цепей будет достигаться в аппарате вытеснения .

Быстрый рост цепей , при котором время роста отдельной цепи мало. За время пребывания в аппарате многократно наступают начало и конец роста цепи. Длина цепи в основном определяется концентрациями мономера и других веществ (инициатора полиме­ризации, регулятора длины и пр.) в период ее роста. Поэтому мо­лекулярной однородности будет способствовать идеальное смеше­ние, выравнивающее концентрации по всему аппарату. В аппара­те вытеснения в этом случае цепи, выросшие в начале аппарата (высокая концентрация мономера), будут сильно отличаться от тех, что выросли в его конце .

Пример 6 . Влияние турбулентности на полимеризацию. Исследована реакция анионной полимеризации стирола с целью полу­чения максимальной молекулярной однородности. Примерно за 1 мс стирол сме­шивали с инициатором и пропускали по трубке (полимеризатору). Среднее вре­мя пребывания составляло от 0,1 до 2 с; после выхода из трубки полимеризация прекращалась.

На рис . 10 показаны интегральные функции распределения степени поли­меризации N , полученные при разных значениях критерия Рейнольдса . Переход от ламинарного потока ( Re = 1000 ) к развитому турбулентному ( Re = 15000 ) привел к резкому снижению дисперсии N .

Модель идеального вытеснения

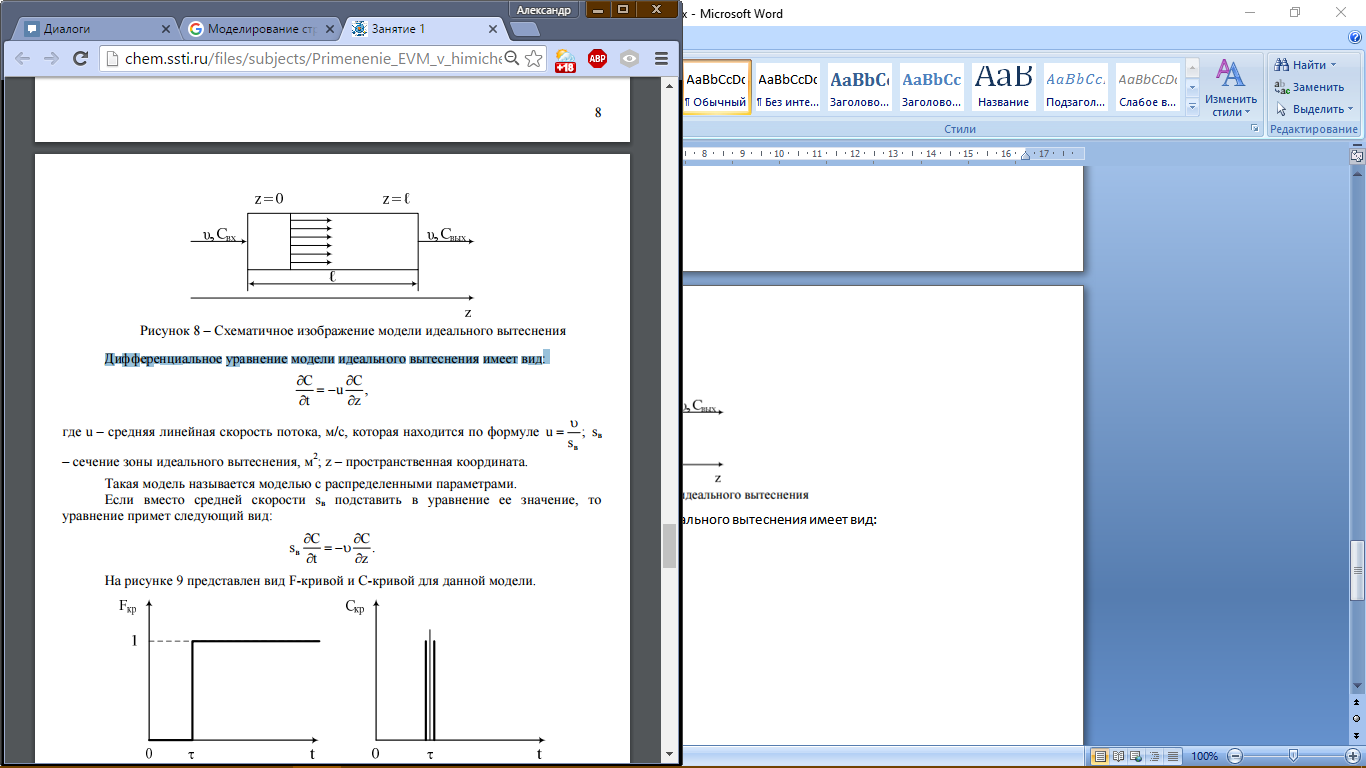
В соответствии с моделью идеального вытеснения принимается поршневое течение без перемешивания вдоль потока при равномерном распределении концентрации вещества в направлении, перпендикулярном движению. При этом время пребывания всех частиц в зоне идеального вытеснения одинаково и равно отношению объема зоны вытеснения к объемному расходу жидкости (или газа) t = V/u . Схематическое изображение модели идеального вытеснения показано на рисунке 8.

Дифференциальное уравнение модели идеального вытеснения имеет вид:

где u – средняя линейная скорость потока, м/с, которая находится по формуле u=v/sв; sв – сечение зоны идеального вытеснения, м 2 ; z – пространственная координата.

Такая модель называется моделью с распределенными параметрами. Если вместо средней скорости sв подставить в уравнение ее значение, то уравнение примет следующий вид:

На рисунке 9 представлен вид F-кривой и С-кривой для данной модели.

Модель идеального вытеснения широко используется в химической технологии при описании трубчатых реакторов и теплообменников.

58. Математическое моделирование химических превращений.

59. Моделирование тепловых процессов.

60. Моделирование систем управления

Огромное значение в управлении деятельностью предприятий в настоящее время играет моделирование, представляющее собой разновидность методов формализованного представления систем. При этом следу-ет подчеркнуть, что моделирование экономи-ческого процесса тесно связано с информа-ционным обеспечением, поскольку предпола-гает использование, как внутренней информации, так и внешней, на основе которой и проводятся различные вычисления для по-строения моделей, поэтому эти методы за-частую рассматриваются в комплексе.
Использование на практике методов моделирования хозяйственных ситуаций позволяет вырабатывать экономически эффектив-ные стратегии и тактически верные управ-енческие решения. При этом количественный анализ и математическая формулировка экономических законов служат переходной ступенью от их качественной трактовки к разработке моделей эффективного развития.
Содержание моделирования составляют конструирование модели на основе предварительного изучения объекта и выделение его существенных характеристик, экспериментальный и/или теоретический анализ мо-дели, сопоставление результатов с данными об объекте, корректировка модели и т.д.
Моделирование какого-либо объекта заключается в замене исходного объекта таким объектом (моделью), исследование которого можно провести эффективнее, т.е. легче, доступнее, быстрее, дешевле и т.д.
Исследование экономических систем посредством моделирования имеет ряд преимуществ перед исследованиями методом эксперимента, которые можно свести к следующим:
— Модели, как правило, удобны в использовании и обходятся дешевле, чем контакт непосредственно с фактической ситуацией.
— Применение моделей требует от пользователей организовывать и дополнять информацию, при этом в процессе работы могут обнаружиться области, где необходима дополнительная информация.
— Модели обеспечивают системный подход к решению проблем.
— Модели дают более ясное понимание проблемы.
— Модели позволяют руководству анали-зировать вопросы типа «а что если. »
— Модели требуют, чтобы пользователи четко определяли цели анализа.
— Модели служат последовательным инструментом для оценки.
— Модели позволяют пользователям использовать «всю мощь математики» для решения проблемы.
— Модели обеспечивают единый подход к анализу проблем.
Существует множество разновидностей моделей:
— графики и таблицы,
— физические модели,
— логические и математические выражения,
— машинные модели,
— иммитационные модели.
Таким образом, имитационное моделирование является эффективным средством решения сложных проблем, а имитационная модель – абстрактным описанием системы.
Выбор конкретного метода формализованного описания, системы управления, зависит от того, в каких условиях осуществляется обследование, какова ответственность исполнителей и степеньи регламентации управления в обследуемой организации.

61. Построение линейных регрессионных моделей. Метод наименьших квадратов.