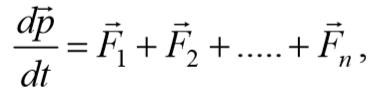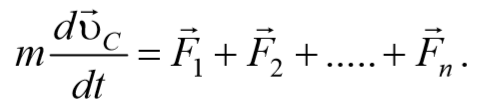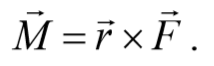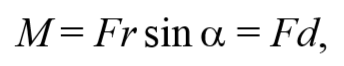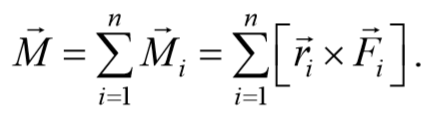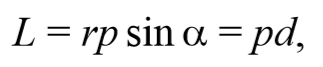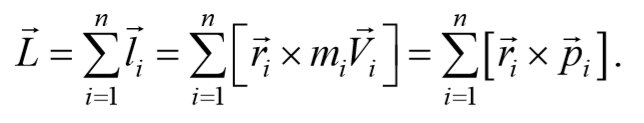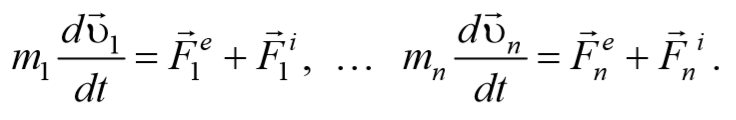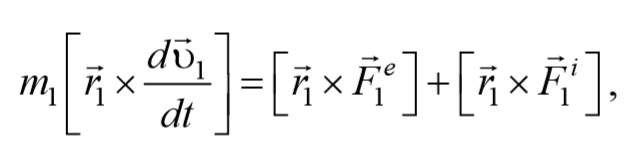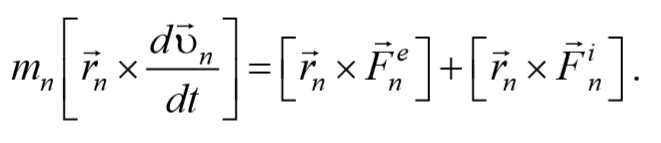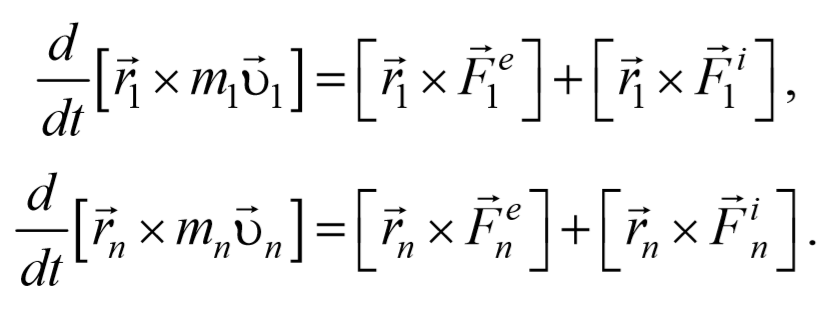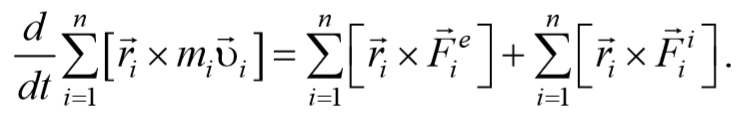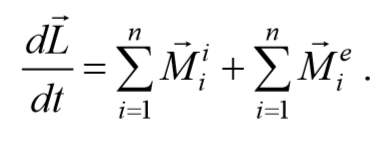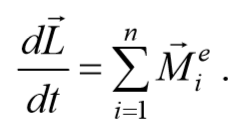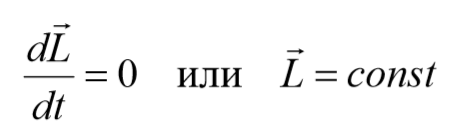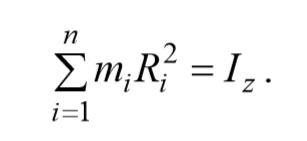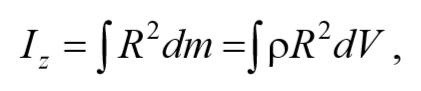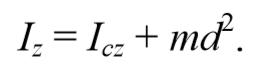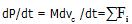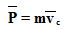Момент импульса для системы материальных точек
Предположим, что точка 












Закон сохранения импульса для системы материальных точек
При произвольном движении системы n материальных точек:
Результирующий момент внутренних сил в соответствии с третьим законом Ньютона равен нулю.
В уравнении (1) операции дифференцирования и суммирования можно поменять местами:
Если внешние силы на систему не действуют, то
Момент импульса замкнутой системы величина постоянная, т.е. с течением времени не меняется – закон сохранения момента импульса.
Система центра инерции
Если тело состоит из N материальных точек с массами mi и радиус-векторами ri, то Систему центра инерции материальных точек называют такую т. С
Радиус-вектор которой равен
mi-общая масса всей системы
m-масса i-той точки
Билет 5
Работа – скалярное произведение силы на перемещение.
A=Fss=Fs cos 
Fs – проекция силы, (Fs =F cos 
dA=Fdr=Fcos 
Мощность- работа совершаемая в единицу времени
N= 
Кинетическая энергия— половина произведения массы тела на ее скорость в квадрате : T=mU 2 /2.
Потенциальная энергия— механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними:
П=mgh- в поле силы тяжести
П=kx^2/2 — в поле силы упругости.
Поля, где работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от траектории, а зависит только от начального и конечного положения, называют потенциальными, а силы, действующие в них – консервативными.
Примером потенциальных сил являются упругие силы тяжести
Пример потенциальной энергии-Мяч бросают с какой-то высоты на землю. В верхней точки он обладает потенциальной энергией, кинетическая равна нулю. С уменьшением высота эта энергия тоже уменьшается. Когда мяч упадет на землю, он покатится. Его потенциальная энергия станет равной нулю, а к0инетическая примет какое-то значение.
Билет 6
Механическая энергия- это физическая величина, которая характеризует способность системы (тела) к совершению механической работы.
Полная механическая энергия – энергия механического движения и взаимодействия: E=T+П, где T=mU 2 /2
Закон сохранения механической энергии:суммарная механическая энергия всех тел сохраняется, если: 1) система тел замкнута, 2) система отсчёта инерциальна, 3) действуют только консервативные силы.
Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости. Рис. 1.20.1 поясняет решение этой задачи.

Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:
Обратим внимание на то, что сила 
При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:
Из этих соотношений следует:
Центростремительное ускорение в нижней точке создается силами 

Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно
Билет 7
Абсолютно твёрдое тело –совокупность точек, расстояние между которыми не изменяется, каким бы взаимодействиям данное тело в процессе движения ни подвергалось.
Угловой скоростьюназывается векторная величина, равная первой производной угла поворота по времени:
Ѡ=dφ/dt
Угловым ускорениемназывается векторная величина, равная первой производной угловой скорости по времени:
Έ=dѠ/dt
Поступательное движение – механическое движение абсолютно твёрдого тела (система точек), при котором отрезок прямой связывающий две любые точки этого тела, форма и размеры которого во время движения не меняются, остаётся параллельным своему положению в любой предыдущий момент времени.
Вращательное движение –механическое движение, где абсолютно твёрдое тело (система точек) описывает окружность. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения.
Лекция №5. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
4.1. Динамика поступательного движения твердого тела.
Движение любого твердого тела можно рассматривать как сумму поступательного движения его центра масс и вращательного движения относительно оси, проходящей через его центр масс.
Разобьем твердое тело на элементарные массы mi , тогда его можно представить как систему материальных точек, взаимное расположение которых остается неизменным. Поэтому для описания поступательного движения тела можно использовать закон изменения импульса механической системы
p = $$<\sum_
Также можно воспользоваться понятием центра масс и к поступательному движению твердого тела применить закон движения центра масс
Центр масс твердого тела движется как материальная точка, в которой сосредоточена масса тела, и на которую действуют все силы, приложенные к телу. Уравнение (4.1.2) дает возможность установить закон движение центра масс твердого тела, если известна масса тела и действующие на него силы. Если тело движется только поступательно, то это уравнение будет определять не только закон движения центра масс, но и любой другой точки тела.
4.2. Момент импульса. Момент силы.
Момент силы. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенному из полюса в точку приложения силы, на силу F называется моментом силы материальнойточки относительно некоторого центра
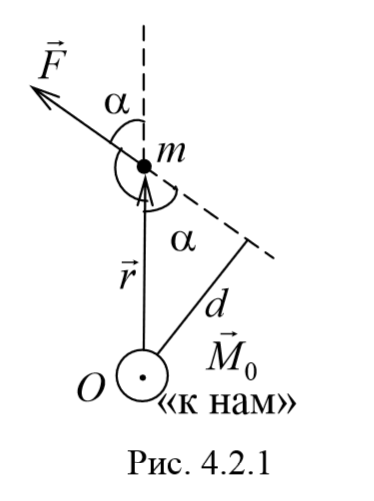
Пусть на частицу массой m действует сила F , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент силы частицы относительно точки O дается уравнением (4.2.1). Направление момента силы M совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора r к силе F , и он перпендикулярен как вектору r , так и вектору F (рис. 4.2.1). Тогда модуль вектора момента силы равен
где d=r sin α − плечо силы относительно точки O .
Плечо силы − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой действует сила.
Таким образом, модуль момента силы относительно оси, есть скалярная величина, характеризующая вращательное движение действия силы и равная произведению модуля силы F , действующей на твердое тело, на плечо силы d относительно этой оси.
Если на тело действует несколько сил, то суммарный момент этих сил равен векторной сумме моментов всех сил относительно данной оси:
Момент импульса. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенного из центра на ее импульс m υ называется моментом импульса материальной точки относительно некоторого центра
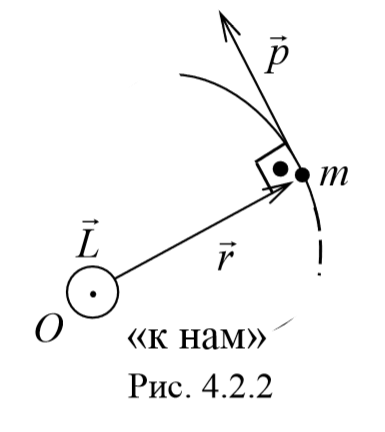
Пусть частица массой m имеет импульс p , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент импульса частицы относительно точки O дается уравнением (4.2.4). Направление момента импульса совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к импульсу p , и он перпендикулярен как вектору r , так и вектору p (рис. 4.2.2). Тогда модуль вектора момента импульса равен
где d − плечо импульса относительно точки O .
Плечо импульса − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой направлен импульс.
Таким образом, модуль вектора момента импульса относительно центра или оси − есть скалярная величина, равная произведению импульса p на плечо импульса d относительно этой оси.
Моментом импульса механической системы относительно некоторого центра называется векторная величина, равная геометрической сумме моментов импульса относительно той же точки всех материальных точек системы
4.3. Основное уравнение динамики вращательного движения относительно точки.
Рассмотрим систему материальных точек массами m1, m2, . mn движущихся со скоростями υ 1, υ 2, . υ n . Пусть на каждую из этих точек действуют: равнодействующие внутренних сил F i 1, F i 2, . F i n , и равнодействующие внешних сил F e 1, F e 2, . F e n .
Запишем уравнения движения частиц:
Умножим каждое уравнение системы (4.3.3) на соответствующий радиус-вектор и получим
Преобразуем данные уравнения
Сложим эти уравнения и получим
В последнем уравнении:
Таким образом, выражение (4.3.6) можно записать в виде
Учитывая, что моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы всегда равна нулю, т. е. $$<\sum_
4.4. Закон сохранения момента импульса.
Если момент внешних сил $$<\sum_
закон сохранения момента импульса.
Если момент внешних сил действующих на механическую систему относительно центра оси равен нулю, то момент импульса системы относительно этого центра с течением времени не изменяется.
Можно сказать, что момент силы при вращательном движении является аналогом силы при поступательном движении, момент импульса − аналогом импульса.
Законы изменения и сохранения момента импульса механической системы можно применить и к вращательному движению твердого тела.
4.5. Момент инерции.
Моментом инерции твердого тела относительно данной оси называется физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси:
Момент инерции зависит только от формы тела и расположения масс относительно оси. [I]=1 кг · м 2 .
Понятие момента инерции было введено при рассмотрении вращения твердого тела. Однако следует иметь в виду, что каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси.
Если тело сплошное, то суммирование в выражении (4.5.1) следует заменить на интегрирование:
где R − расстояние от элементарной массы dm до оси вращения.
4.6. Теорема Штейнера. Правило аддитивности
Существуют два свойства момента инерции:
1) Теорема Штейнера: момент инерции тела Iz относительно произвольной оси равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:
2) Правило аддитивности: сумма моментов инерции частей системы относительно оси равен моменту инерции системы относительно данной оси:
Момент силы, момент импульса материальной точки и системы материальных точек
Система материальных точек. Закон сохранения импульса замкнутой системы. Центр масс. Закон движения центра масс.
Система материальных точек – совокупность тел, выделенных для рассмотрения(механическая система).
Закон сохранения импульса. При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.
Если система замкнута ,то dp/dt=0, вектор Р = const.
Центер масс (ц. инерции) сист. МТ, называется т. С радиус вектор которой относительно произвольно выбранной точки О = отношению суммы произведений масс всех матер. точек системы на их радиус векторы из этой точки О к массе угла поворота.
Закон движения центра масс.
Воспользовавшись законом изменения импульса, получим закон движения центра масс:
Центр масс системы движется так же, как двигалась бы частица с массой, равной массе системы, под действием силы, равной векторной сумме всех внешних сил, действующих на входящие в систему частицы.
Скорость движения центра масс:
Момент силы, момент импульса материальной точки и системы материальных точек
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, Символ момента силы M . Момент силы иногда называют моментом пары сил. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси вращения рычага, есть момент силы. Более точно, момент силы частицы определяется как векторное произведение:
M = [r*F] , где (M,r,F — вектора) F— сила, действующая на частицу, а r — радиус-вектор частицы.
Моментом силы F относительно некоторой точки О (расположенной на оси вращения) называют физическую векторную величину, численно равную произведению модуля этой силы и длины перпендикуляра (плеча), проведённого из данной точки на линию действия силы, т. е. M(F)=Fd.
Вектор момента силы направлен вдоль оси вращения. Его направление определяется по правилу буравчика, согласно которого, если ручка буравчика поворачивается в направлении вращения, то его остриё движется в направлении вектора момента силы.
Момент импульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Момент импульса L м.т. и относительно неподвижной т. О называется векторное произведение радиуса вектора r мат. Точки , проведенного из т. О в т. приложения импульса на импульс этой мат. точки.
Момент импульса механической системы. мат. точек относительно неподвижной т. О называется вектор 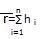
http://physics.belstu.by/mechanics_lk/mechanics_lk5.html
http://lektsii.org/6-73513.html