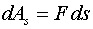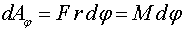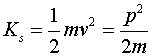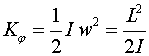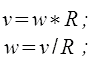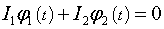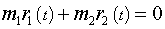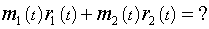Уравнение моментов для вращательного движения является аналогом

Вывод второго закона Ньютона для вращательного движения + примеры решения задач

Второй закон Ньютона для вращательного движения – главное тождество динамики, помогающее решить основную задачу механики для вращающегося тела: указать угол поворота тела в любой промежуток времени.

Задача механики поступательного движения считается решенной если в любое мгновение легко указать положение материальной точки относительно других тел, при условии, заданной системы отсчета.

Кроме поступательного существует вращательное движение – это такой вид движения при котором каждая точка движется по окружности, центры окружности лежат на одной прямой (оси вращения).

Характеристики вращательного движения:

• Всякая точка абсолютно твердого тела перемещается по дуге круга;
• «Ядра» окружностей расположены вдоль одной линии – ось вращения
• Разные точки передвигаются по разным траекториям;
• Зависимости перемещения по времени представляют отличные значения, изменяющиеся по направлению;
• Углы поворота точек – одинаковы.

Аналоги характеристик поступательного и вращательного движения

Параметры вращательного перемещения необходимо рассматривать, проводя сравнение с характеристиками поступательного.

Последовательность нахождения координат тела в любой момент времени для поступательного перемещения:

1. зная силу F находим ускорение a;
2. из ускорения находи координаты x,y,z.

Пойдем от обратного для вращательного движения:

Найти нам необходимо угла поворота – φ в любой момент времени, для этого используем угловое ускорение ε, а вот аналог силы F мы пока не знаем.

Опишем кинематику вращательного движения.

• Аналог линейной скорости во вращательном движении это угловая скорость ω — выражается отношением:

— угол поворота

— незначительный отрезок времени

• Вспомним формулу линейной скорости υ точки находящейся на вращающемся теле, для этого умножим угловую скорость ω и r — расстояние от оси до искомой точки.

Виды вращательного движения:

Поворот предмета за равные промежутки времени на одинаковые углы говорит о равномерности перемещения. Угловое ускорение отсутствует.

Уравнение движения выглядит:

— угол поворота в любой момент времени,

— начальный угол поворота

Угловая скорость постоянна, но линейная скорость постоянно изменяет направление, а это означает, что существует центростремительное ускорение, направленное по радиусу к центру окружности.

1. Неравномерное вращение

При неравномерном перемещении постоянное угловое ускорение принимает вид:

При низменном , закон изменения угловой скорости получается:

Подставляя полученные данные в формулу движения при равномерном вращении получим:

Вспомним как рассчитать угол поворота тела тремя разными способами:

Второй способ (через среднюю скорость).

Сравнение формул вращательного и поступательного перемещения наглядно представлено таблично.

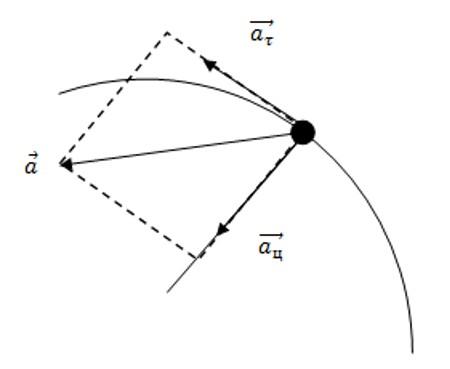
При нахождении точки на теле, неравномерно вращающемся на окружности, ускорение приобретает вид суммы:

— центростремительного и тангенциального

— тангенциального .

Сумма ускорений равна:

Тангенциальное ускорение вычисляется следующим образом

Используя связь υ и ω, получается:

Нужно сформулировать ключевые тождества, включая 2 закон сэра Ньютона для вращательного механического движения, сопутствующие обозначения, необходимые в ходе решения задач.

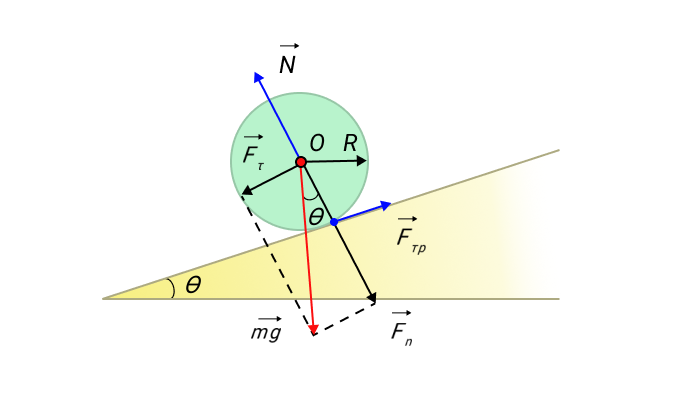
Вывод второго закона Ньютона для вращательного движения

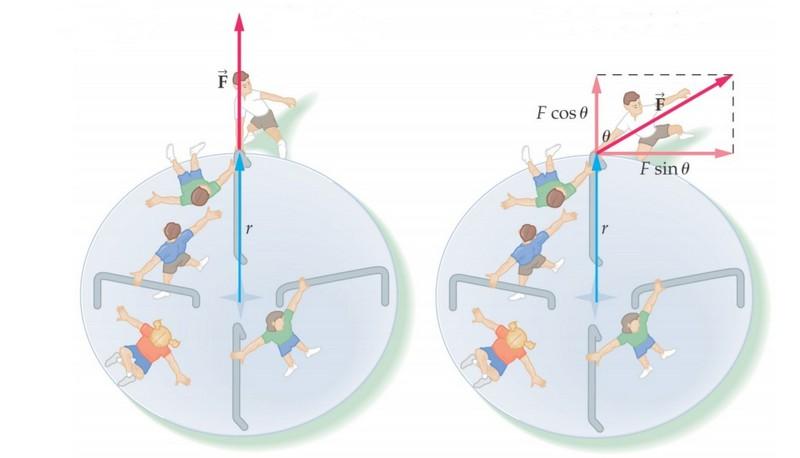
Пусть тело, характеристиками которого можно пренебречь закреплено на невесомом стержне, 0 – ось вращения, длиной эквивалентной отрезку r.

На материальную точку оказывает воздействие силы , – реакция стержня.

— сила реакции нити;

— сила приводящая тело в движение

По II закону английского физика Исаака Ньютона второй закон динамики в векторной форме выглядит:

Выбор системы координат: Y – направляется по радиусу, Х – перпендикулярно.

Переписывая главное правило динамики в проекциях на эти оси:

Для этого на рисунке отобразим угол и выразим через него все проекции.

OX: ,

OY: ,

Из рисунка видно, что — тангенциальное ускорение, и – модуль центростремительного ускорения

Вспомним, что тангенциальное ускорение равно:

Перепишем уравнение проекции на ось x с учетом этого знания:

Вычислим угловое ускорение из полученной формулы:

Умножая на дробь на :

Далее надо визуально отобразить на рисунке rsinα.

Как видно из полученного рисунка перпендикуляр d – плечо силы F.

Сравнивая с выражением:

I=mr 2 – мера инертности тела, момент инерции.

Выходит: 2 закон Ньютона представлен для вращательного движения:

Словесная формулировка основного тождества динамики вращательного перемещения:

Алгебраическая сумма моментов сил, действующих на тело тождественно произведению момента инерции тела на его угловое ускорение.

Практическое применение второго закона Ньютона для вращательного движения

Перемещение путем вращения часто находит практическое применение. Яркие примеры:

• Колеса транспортных средств;
• Шестеренки;
• Роторы электродвигателей.

Простые «мозголомки» из школьного курса физики

Задание 1. Велосипедное колесо

Определить меру инертности у велоколеса диаметром 67 см с массой 1,3 кг? Возможно, не учитывать массу ступицы?

Колесо целесообразно разбить на N мельчайших фрагментов размером Δl с массой Δm.

Мера инертности вычисляется из выражения:

кг х м 2

Задача 2. Взаимодействие кинематики и динамики

Материальная точка перемещается по окружности, ее радиальное ускорение изменяется пропорционально четвертой степени времени. Найти n из отношения .

Записывается второй закон Ньютона для вращательного движения:

Выражая угловую скорость:

Учитывая, неизменность расстояния до центра окружности, :

Упражнение 3. Графическое представление

Одно тело вращается по зависимости 1, потом действие момента сил изменяется согласно графику 2. Нужно сравнить угловые скорости в точках A и B.

Основной закон динамики перемещения путем вращения:

Поскольку тело одно, 1/I неизменно.

Геометрический смысл интеграла – площадь криволинейных трапеций.

Случай 1:

График 2:

Результат:

Получается:

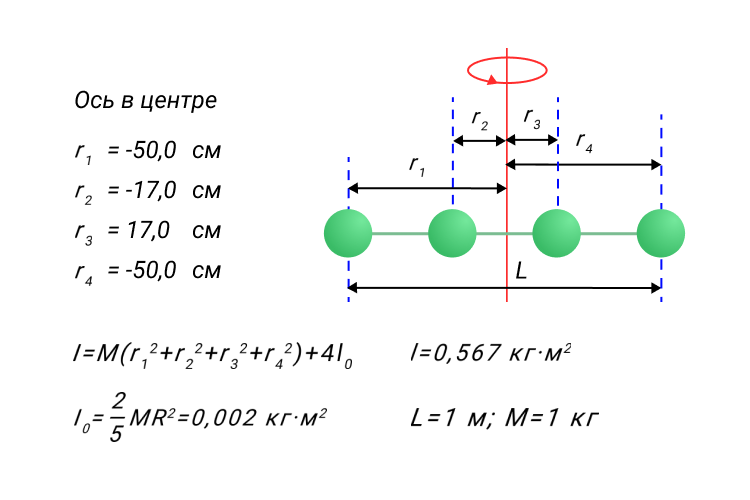
Задание 4. Шары

Два точечных шарика, обладающие равными массами скреплены тонкой невесомой спицей l. Записать выражение момента инерции системы, относительно оси, перпендикулярно соотносящейся со спицей и центром масс.

Центр оси расположен между шарами:

Мера инертности системы:

Упражнение 5. Гири

Грузы массами 2 и 1 килограмм связаны ниткой, перекинутой через блок, весящий 1 килограмм. Вычислить ускорение перемещения гирь? Рассчитать натяжение нитей?

Векторный вид поступательного передвижения:

Перемещение диска – вращение:

Первые 2 равенства надо спроектировать на Х, последнее – Y. Записать уравнение кинематической связи. Получается система:

Подставляя 4 тождество в 3:

Вычитая (2) из (1), переписывается (5):

Численное значение из выражения (6) подставляется в (1) и (2):

Практическое применение в жизни

Автомобиль

Ускорится автомобиль, если установить шины большего диаметра?

Нет. Чем больше диаметр шин, тем выше линейное ускорение. Каждый автомобиль обладает максимальным угловым ускорением, соответствующее его мощности. Мощность машины ограничена, увеличение диаметра шин приведет к снижению углового ускорения, линейное не изменится.

«Что-то странная какая-то утка, на курицу похожа…»

Домашние птицы: селезень и курица имеют одинаковую длину шага. Почему курица бегает ровно, а селезень перемещается переваливаясь?

Расстановка лап селезня шире, центр тяжести расположен дальше от опоры, поэтому при ходьбе селезень вынужден делать поворот на больший угол. Момент силы тяжести от опоры увеличивается, соответственно становится больше величины угловых ускорения и скорости.

Гонки

Европейские гонки проходят по улицам города, поэтому гонщики не снижая большой скорости совершают резкие повороты. Двигатель гоночных машин расположен посередине авто. Содержание преимущества?

Двигатель посередине авто, обладает меньшей мерой инертности относительно центра масс, поэтому поворот осуществляется при меньшем моменте сил.

Фигурное катание

Зачем фигурист прижимает руки к телу?

Фигурист, вращаясь вокруг вертикальной оси, прижимает руки к корпусу. Момент инерции уменьшается, момент импульса остается неизменным, угловая скорость увеличивается.

Невесомость

Космонавт находится в невесомости. Как ему совершить поворот на 180˚ вокруг продольной оси?

Распутывание Гордиева узла:

Для поворота космонавт поднимает руку над головой, провоцируя поступательные движения в направлении, противоположенному повороту.

О кошках

Эмиль Кроткий утверждал: «Кошка мечтала о крыльях: ей хотелось попробовать летучих мышей». Люди не раз пытались подкидывать животное вверх ногами, при этом приземление всегда осуществляется на лапы. Момент внешних сил равен нулю, момент импульса сохраняется. Как кошке удается переворачиваться?

Момент импульса кошки, находящейся в свободном падении остается постоянным, моменты внешних сил отсутствуют. Вытягивая или прижимая к телу лапы, кошка изменяет меру инертности передней части тела относительно центральной оси от момента инерции задней части тела. Попеременно подтягивая передние или задние лапы, животное совершает поворот, ускоряющийся вращением хвоста.

Освоение 2 закона Исаака Ньютона с учетом кинематических и динамических характеристик для вращательного механического движения на практических примерах – легкое задание: надо запастись терпением, желанием приобретать знания. Изучать физику лучше вооружившись высказыванием Морихэй Уэсибы: «Двигайся, как луч света, летай, как молния, бей, как гром, вращайся вокруг устойчивого центра!»

Уравнение моментов для вращательного движения является аналогом

Используя метод аналогий, можно предположить, что должна существовать замкнутая механическая система,
способная изменять свое положение в пространстве только с помощью внутренних сил, без воздействия извне.

Метод аналогий. Метод исследования какого-либо процесса, путём замены его процессом,
описываемым таким же дифференциальным уравнением,
как и изучаемый процесс.
(Толковый словарь физических терминов)

Аналогия между вращательным и поступательным движениями

« Я ценю умение строить аналогии, которые, если они смелы и разумны,
выводят нас за пределы того, что пожелала нам открыть природа,
позволяя предвидеть факты ещё до того, как мы их увидим . ».
Ж.Л.Д’Аламбер

Между движением твердого тела вокруг неподвижной оси и движением отдельной материальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вращения твердого тела. Координате s соответствует угол φ , линейной скорости v — угловая скорость w , линейному (касательному) ускорению а — угловое ускорение ε .

Сравнительные параметры движения:

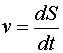
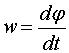
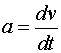
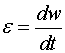
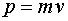
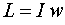
Таблицу можно продолжать и далее.

Выражения для вращательного движения напоминают соответствующие выражения поступательного движения.
Они получаются из последних формальной заменой m => I , v => w , p => L

Выражения имеют не просто формальное сходство.
Поступательное движение можно рассматривать, как вращательное, с радиусом вращения, стремящимся к бесконечности, и угловой скоростью, стремящейся к нулю.

Представленная таблица не может претендовать на всю полноту охвата аналогичных значений.
Для вращательного и поступательного движений формулируются и аналогичные законы:

Закон сохранения импульса (ЗСИ )

,при F _внеш = 0

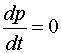
Закон сохранения момента импульса (ЗСМИ )

, при M _внеш = 0

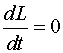
«Если геометрическая сумма внешних сил, действующих на систему, равна нулю, то импульс системы сохраняется, т.е. не меняется со временем. В частности, это имеет место, когда система замкнута»

«Если момент внешних сил относительно неподвижного начала О равен нулю, то момент импульса системы относительно того же начала остается постоянным во времени»

[Д.В.Сивухин. Общий Курс Физики. т.I Механика]

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Однако, этот закон сохранения верен и в случаях, когда Ньютоновская механика неприменима (релятивистская физика, квантовая механика). Он может быть получен как следствие интуитивно-верного утверждения о том, что свойства нашего мира не изменятся, если все его объекты (или начало отсчета!) переместить на некоторый вектор r. В настоящее время не существует каких-либо экспериментальных фактов, свидетельствующих о невыполнении закона сохранения импульса.

Закон сохранения момента импульса является следствием утверждения о том, что свойства окружающего мира не изменяются при поворотах (или повороте системы отсчета) в пространстве. Момент импульса системы точечных тел L определяется как сумма моментов каждой из точек и сохраняется во времени при условии равенства нулю момента внешних сил. Данные законы относятся к глобальным законам сохранения.

Ответ на естественный вопрос о том, почему справедливы законы сохранения, в физике был найден сравнительно недавно. Оказалось, что законы сохранения возникают в системах при наличии у них определенных элементов симметрии. (Элементом симметрии системы называется любое преобразование, переводящие систему в себя, т.е. не изменяющее ее).

Немецкий математик Эмми Нётер в 1918 году математически доказала связь между законами сохранения и симметрией, которой обладают в физике законы природы. В упрощенной формулировке теорема Нётер гласит, что если свойства системы не меняются от какого-либо преобразования переменных, то этому соответствует некоторый закон сохранения.

Теорема Нётер — самое простое и универсальное средство, позволяющее находить законы сохранения в классической механике, квантовой механике, теории поля и т.д.
Вот как выглядят доказательства ЗСИ и ЗСМИ на основании свойства симметрии пространства
[Д.В.Сивухин. Общий Курс Физики. т.I Механика.(гл.Y,§38)] :

.

…4.Перейдем к доказательству закона сохранения импульса. Допустим, что механическая система замкнута. Все силы F₁ , F₂ , . действующие на материальные точки системы, являются силами внутренними, внешних сил нет. Перенесем систему из произвольного положения 1 в другое произвольное положение 2, чтобы все материальные точки ее претерпели одно и то же смещение r, и притом так, чтобы их скорости остались прежними по величине и направлению. Ввиду однородности пространства, на такое перемещение не требуется затраты работы . Но эта работа представляется скалярным произведением (F₁ +F₂ + . )r . Значит, оно равно нулю, каково бы ни было смещение r. Отсюда следует, что для замкнутой системы F₁ +F₂ + . =0. А это есть как раз то условие, при выполнении которого из второго закона Ньютона получается закон сохранения импульса.

5. Закон сохранения момента импульса для замкнутой системы доказывается в точности так же. Используя изотропию пространства, можно доказать, что геометрическая сумма моментов внутренних сил, действующих в системе, равна нулю: М₁ +М₂ +. =0. Отсюда немедленно следует рассматриваемый закон

Как видно, доказательства очень похожи.
При всей схожести поступательного и вращательного движений, у них есть и различия.
Одно из них и рассматривается в данной статье.

Существует явление, вступающее, казалось бы, в противоречие с ЗСМИ.

Замкнутую механическую систему можно повернуть на любой угол с помощью одних только внутренних сил.

И не только повернуть, но и заставить вращаться .

Как можно повернуть механическую систему с помощью одних только внутренних сил?
Рассмотрим пример.

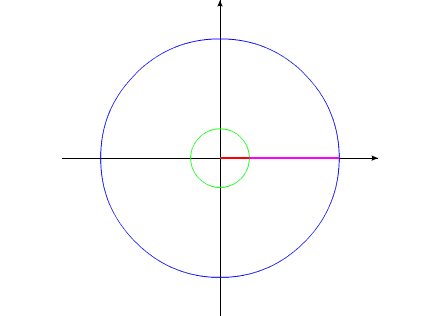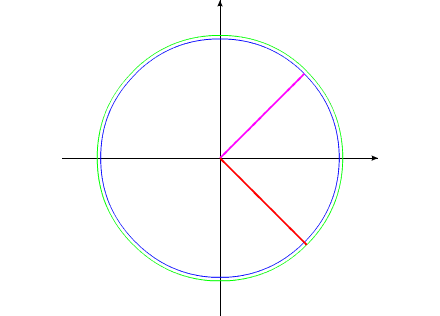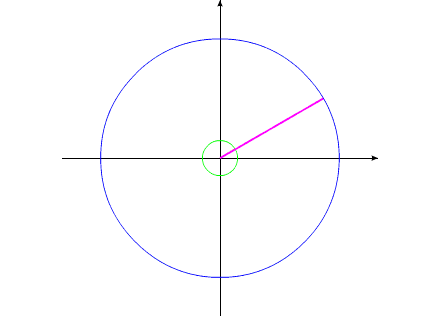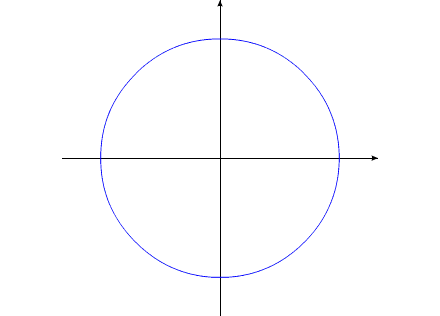
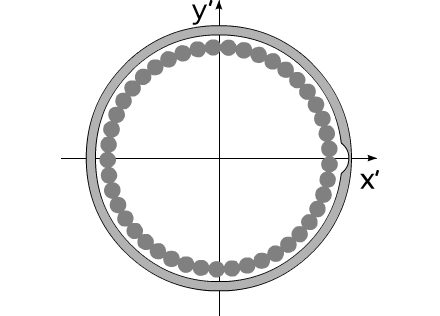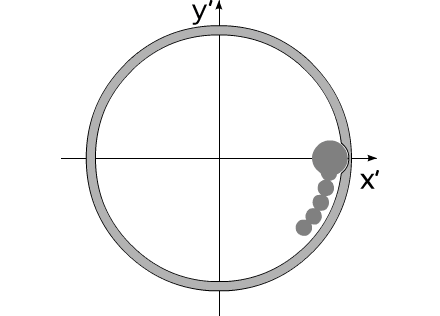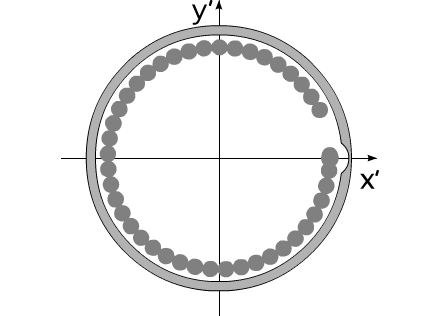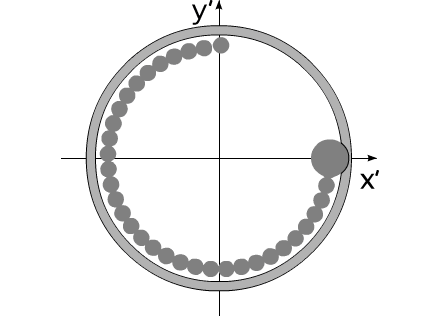
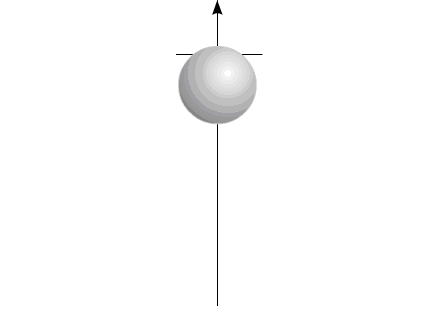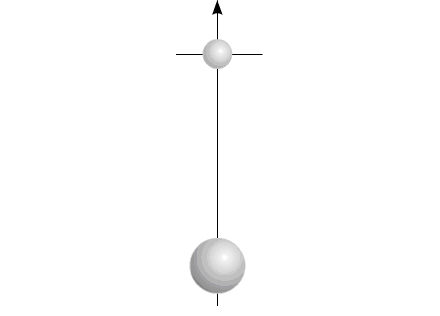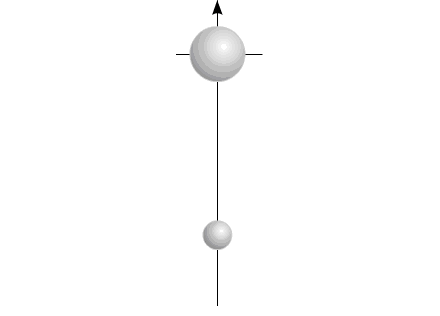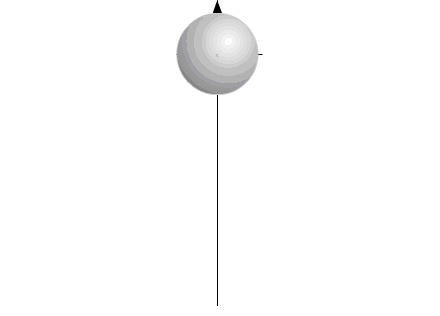
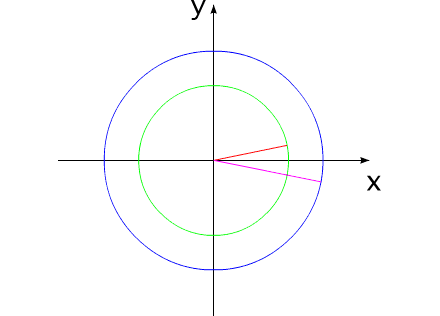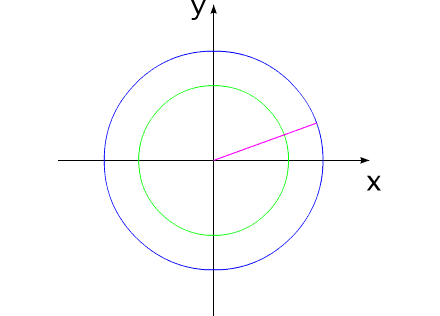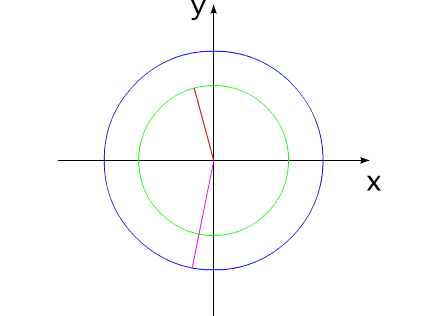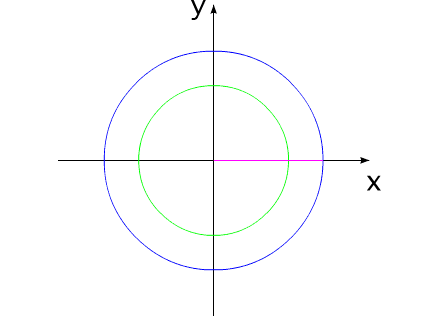
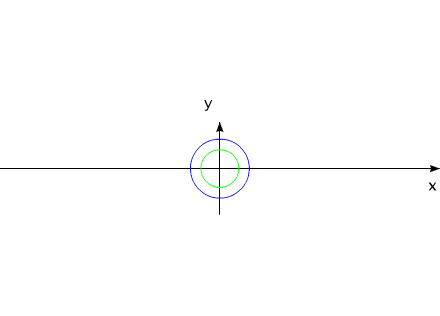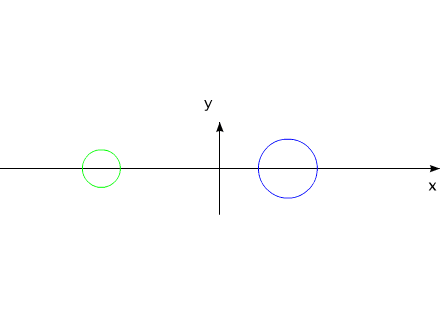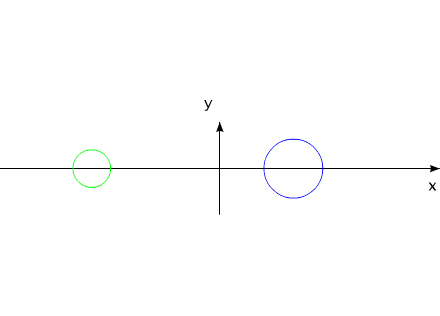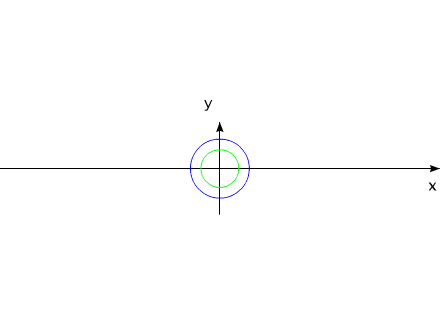
Допустим, у нас имеется два уравновешенных тела, закрепленных соосно. Тела имеют возможность вращаться относительно друг друга. Одно из тел (зеленый контур, красный радиус) способно изменять свои геометрические размеры, изменяя, тем самым, свой момент инерции (I_v). Допустим, максимальное значение I_{v max} этого тела соответствует значению I_c второго тела (синий контур, пурпурный радиус). Минимальное значение I_{v min} значительно меньше I_{v max}.

Рассмотрим циклы движения данной механической системы.

Тело с переменным I_v приобретает максимальные геометрические размеры. (За счет внутренней энергии, разумеется).

За счет той же внутренней энергии создадим внутренний момент, действующий одинаково на оба тела. Под действием этого момента, тела начинают поворачиваться в противоположные направления.

Можно остановить движение обоих тел в любой момент времени. Поскольку моменты инерции обоих тел равны, то и угловые положения оба тела займут одинаковые (по абсолютной величине). В момент останова, угловое положение всей системы осталось прежним. Не изменится это угловое положение и тогда, когда мы начнем изменять геометрические размеры одного из тел.

Уменьшив геометрический размер, и соответственно момент инерции одного из тел, попробуем свести оба тела к прежним угловым положениям этих тел, с помощью силового момента, направленного в другую сторону.

Вот тут и происходит интересное.

Поскольку моменты инерции обоих тел уже различны, то оба тела повернутся на разные углы. Можно опять увеличить размеры одного из тел. Система вновь будет такой, как и прежде.
Почти…
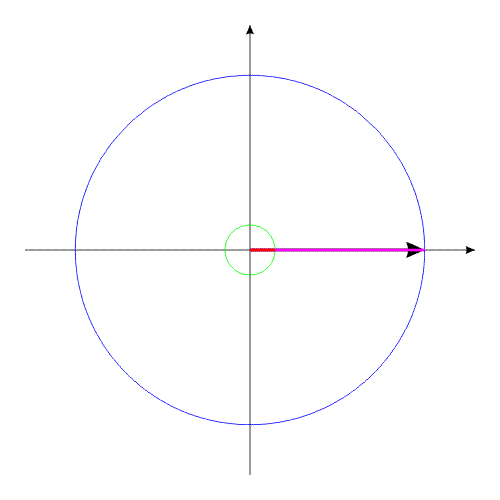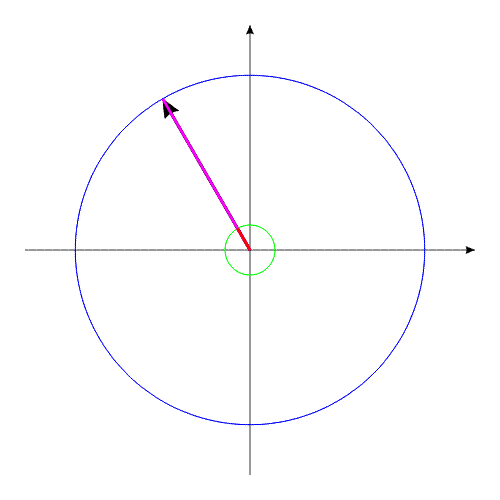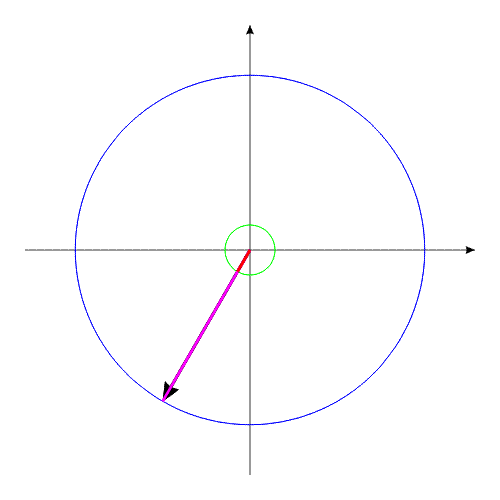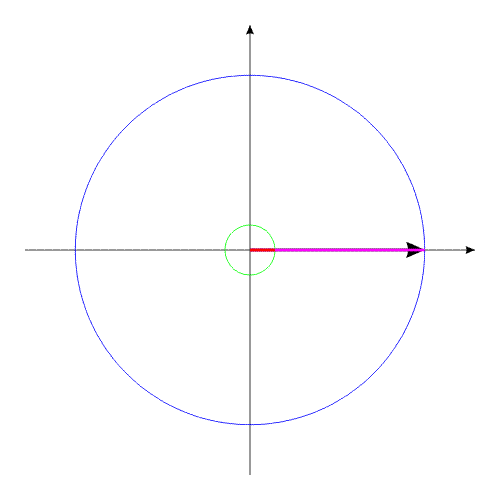
На самом деле, вся система оказывается повернутой на некоторый угол.
Величина этого угла пропорциональна разнице моментов инерции двух тел.

Эти циклы движения можно повторять.
И оказывается, что система вращается!

Причем, вращается совсем неплохо!

Допустим, компоненты системы изменяют свои геометрические размеры таким образом, что суммарный момент инерции всей системы остается без изменений.
Изображенную на рис.3 систему можно рассматривать, как взаимодействие тел с переменным моментом инерции, при неизменной массе и неизменном моменте инерции всей системы в целом.

Система, изображенная в анимационном рис.3, совершает полный оборот за 16 секунд.
Можно даже вычислить скорость вращения этой системы:

[рад/с]

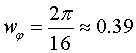
Но, на самом деле, нельзя говорить об этой величине, как о «скорости вращения системы». Правильнее будет звучать: «скорость процесса изменения углового положения», так как величина w _φ не является мерой кинетического состояния данной системы, поскольку кинетическая энергия системы не изменяется.

Рассмотренное движение является безынерционным (движением без инерции!). Если остановить относительные перемещения компонентов внутри замкнутой системы, движение w _φ немедленно прекращается. К величине w_φ более всего подходит название скорость прецессии. безинерционное

В процессе подобного вращения не нарушается ЗСМИ, поскольку суммарный момент импульса всех компонентов системы, в каждый момент времени, равен нулю.

В то же время можно определить момент силы, эквивалентный внешнему моменту силы, который необходимо было бы приложить к системе, чтобы вызвать подобное перемещение.
Именно – эквивалентный, поскольку для рассматриваемой ситуации, внешний силовой момент равен нулю.

Выводы, которые можно сделать на основании приведенного примера:

• в рамках Закона Сохранения Момента Импульса можно изменять угловые координаты замкнутой механической системы только за счет внутренних сил;
• важную роль при организации углового перемещения с помощью внутренних сил, играет изменение момента инерции компонентов системы;
• угловое перемещение всей системы — безынерционно;
• скорость изменения угловых координат, имея размерность такую же, как и угловая скорость, скоростью может считаться только формально.

Вернемся к доказательствам ЗСИ и ЗСМИ на основании свойства симметрии пространства.

Доказательства строятся на допущении некоторого смещения системы (поворота, в случае ЗСМИ).
Но в случае вращающейся системы, это смещение действительно можно произвести за счет внутренней энергии.
То есть, смещение не виртуально, а вполне реально.

В большой таблице аналогичных выражений для вращательного и поступательного перемещений, появляется большая пустая ячейка:

Перемещение за счет внутренних сил

Поворот за счет внутренних сил

φ ≠const при: ∑L_i = 0 , 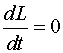, M _внеш = 0

Перемещение за счет внутренних сил?
В случае с поступательным перемещением, такое, кажется, недопустимо. На этот счет даже существует «Теорема о движении центра масс», которая, на первый взгляд, не допускает подобное перемещение:
«Центр масс системы движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила — геометрической сумме всех внешних сил, действующих на систему».

Значит, пустую ячейку в таблице должна занимать данная теорема?
Но метод аналогий позволяет предположить, что и для линейно перемещающейся системы, должны существовать возможности, присущие вращающейся системе.
Это предположение строится на аналогичности уравнений движения вращательного и поступательного движений.
Ячейка должна быть заполнена, примерно, следующим содержанием:

Перемещение за счет внутренних сил

s ≠const при: ∑ p _i = 0 , 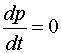, F _внеш = 0

Это выражение получается в результате формальной замены φ => S , M => F , L => p

Выводы, которые можно сделать с помощью метода аналогий:

• возможно существование механической системы, которая способна линейно перемещаться только за счет внутренних сил;
• линейное перемещение может осуществляться за счет изменения параметра, аналогичного моменту инерции, а именно – массы;
• линейное перемещение всей системы должно быть безынерционным;

«скорость» перемещения подобной системы не будет являться мерой кинетического состояния, т.е. в процессе перемещения суммарный импульс компонентов системы будет оставаться неизменным.
Поскольку «скорость» при таком движении является величиной формальной, её появление не может служить признаком нарушения «Теоремы о движении центра масс».

Свойства механической системы, под названием «варипенд«, полностью удовлетворяют перечисленным предположениям.

Название «варипенд» получено от слияния двух слов: varipend =variable +pendulum (переменный маятник).

В процессе перемещения рабочей массы и её остановке в «корпусе» системы, движение центра масс рабочего вещества можно рассматривать, как движение маятника переменной длины и переменной массы. (В системе координат, связанной с корпусом)

Или, в проекции на одну координату:
(Такой случай перемещения центра масс возможен при перемещении двух рабочих масс, вращающихся в противоположных направлениях.)

Изменяющийся размер компонентов на рисунке символизирует изменение массы элементов системы:
рабочего вещества, уменьшающего свою массу за рабочий период,
и корпуса системы, увеличивающего свою массу за счет присоединения частиц рабочего вещества.

При неизменной общей массе, всю систему можно рассматривать, как взаимодействие компонентов переменной массы.

Единственной причиной изменения импульса корпуса является приобретение корпусом элементарных импульсов рабочей массы. При этом корпус увеличивает свою массу.
Единственная причина изменения импульса рабочей массы – потеря элементарных импульсов частиц рабочей массы. При этом масса рабочего вещества уменьшается.
При этом изменение импульса всей системы равно нулю.
И суммарный импульс всей системы также равен нулю!

В одном из расчетов перемещения «варипенда» используется уравнение движения тела переменной массы – уравнение Мещерского.

Расчет перемещения данной механической системы с помощью уравнений Лагранжа также приводит к интересному результату.

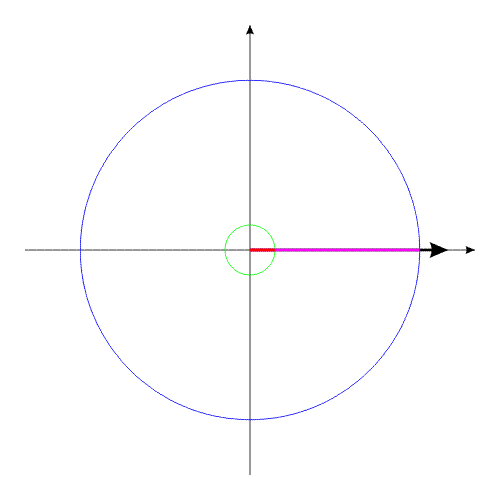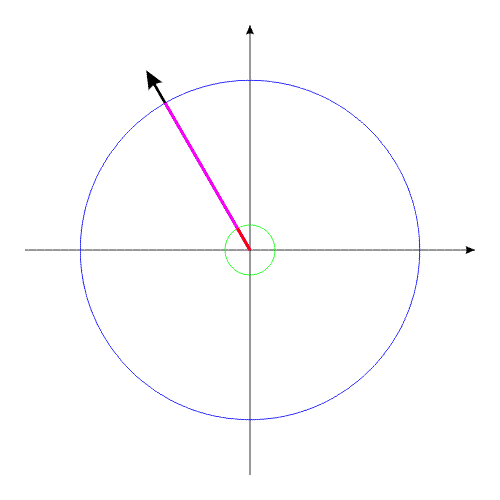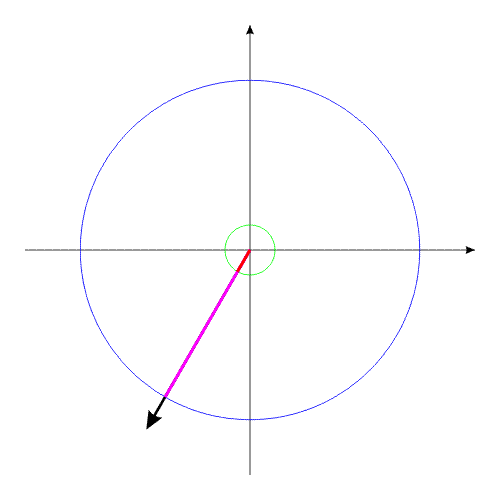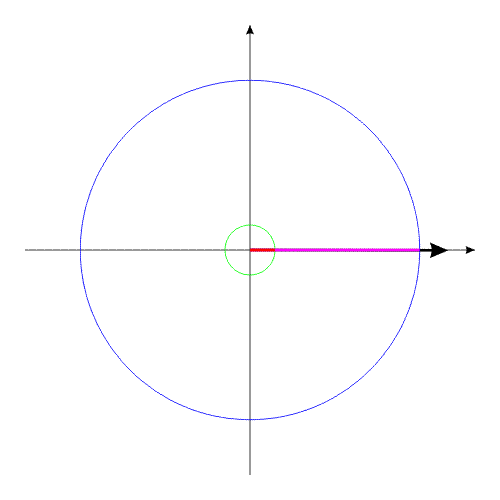
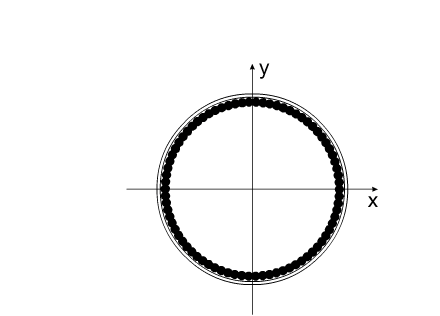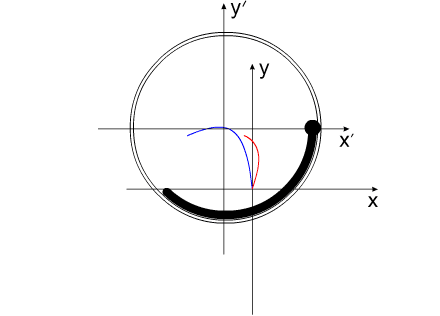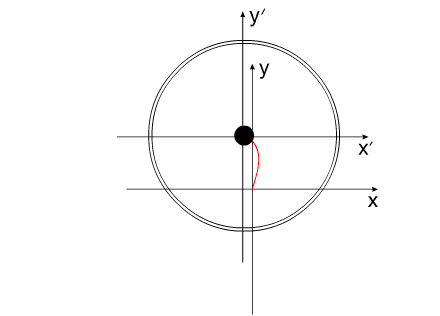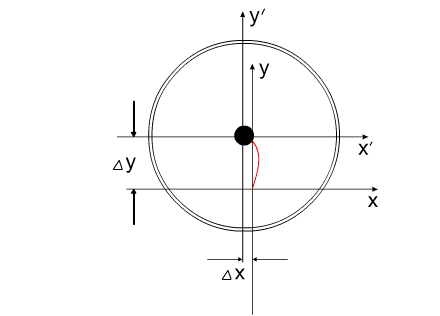
На рис.4 представлена постановка задачи «варипенд».
Решение этой задачи выглядит следующим образом:

Синим цветом показана траектория перемещения корпуса.
Красным — перемещение Центра Масс всей системы.

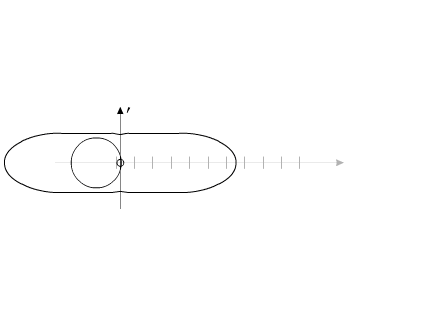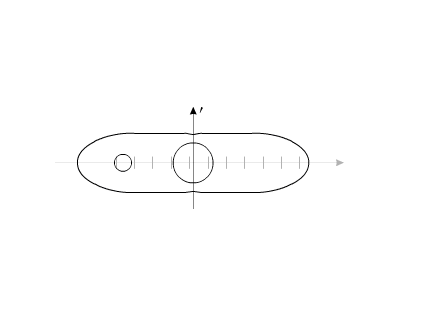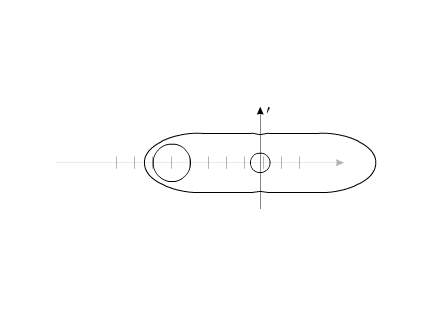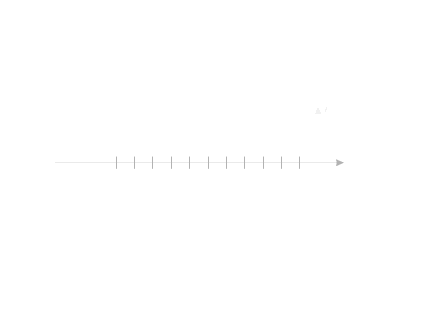
Если рассматривать «варипенд» в абсолютной системе координат, то при повторении внутренних циклов перемещения рабочего вещества, «варипенд» непрерывно изменяет свое положение в пространстве:

Можно провести аналогию с рисунком 3.
Система, изображенная на рис.8, перемещается на расстояние 55 мм за 20 секунд.
Казалось бы, можно подсчитать скорость «варипенда»:

[мм/с]

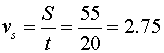
Но так как в процессе перемещения суммарный импульс системы остается неизменным, величина v _s будет являться величиной формальной, определяющей только изменения координат центра масс. Эта величина никак не связана с импульсом всей системы.

Перемещение «варипенда» является безынерционным .
Если остановить относительное перемещение рабочей массы внутри замкнутой механической системы, вся система мгновенно прекратит свое движение.

Математические расчеты, описывающие свойства механической системы под названием «варипенд», можно посмотреть по адресу:
https://varipend.narod.ru

Во многих учебных изданиях по Теоретической Механике, приводятся примеры поворота замкнутой механической системы за счет внутренних сил.
Например, человек способен повернуть себя на скамье Жуковского, совершая некоторые вращения руками.
Поворачивая массивные тела в космическом летательном аппарате, производят угловую ориентацию этих аппаратов.
Космонавт, находясь в невесомости, также может повернуть свой корпус, совершив несколько оборотов рукой.

Однако, на самом деле, во всех приведенных примерах поворот системы отсутствует.
Приведенные примеры демонстрируют, если можно так выразиться, «» замкнутой механической системы.
Попытаюсь пояснить свои слова.
Если моменты инерции компонентов системы не изменяются и внешний момент отсутствует, то можно записать:

Это легко проверить.
Допустим, мы поворачиваем два тела друг относительно друга.
Если после остановки поворачивать компоненты в противоположную сторону, система обязательно займет точно такое же угловое положение, которое было в начальный момент времени.

На рис. 9 два тела сначала поворачиваются на некоторый угол, а затем поворачиваются в противоположную сторону на точно такие же углы. При этом система занимает свое прежнее угловое положение.
Иллюзия поворота всей системы возникает из-за того, что угловая функция периодична. Как только угловые положения компонентов превышают угол 2 π , возникает ощущение, что система повернулась. Но это не так. Конечно же, углы необходимо продолжать отсчитывать и при превышении угла 2 π.

Аналогичным примером линейного перемещения может служить случай взаимодействия двух тел, обладающих неизменной массой:

Тела могут удалятся друг от друга, за счет внутренних сил, приближаться, но для данной системы всегда будет выполняться соотношение:

Это — следствие теоремы о движении центра масс.

А как будут выглядеть те же выражения для условий системы, состоящей из компонентов с переменным моментом инерции (переменной массой)?:

» . аналогия является специфическим случаем симметрии, особым видом единства сохранения и изменения. Следовательно, использовать в анализе метод аналогии, — значит действовать в соответствии с принципом симметрии. Аналогия не только допустима, но и необходима в познании природы вещей. » [Овчинников Н. Ф. Принципы сохранения,.М.,1966]

Защищено законодательством Российской Федерации по авторским правам.
Никакая часть сайта не может быть воспроизведена в какой бы то ни было форме
и какими бы то ни было средствами без письменного разрешения владельца авторских прав.

Вращение твердого тела

Для кинематического описания процесса вращения твердого тела нужно ввести такие понятия как угловое перемещение Δ φ , угловое ускорение ε и угловая скорость ω :

ω = ∆ φ ∆ t , ( ∆ t → 0 ) , ε = ∆ φ ∆ t , ( ∆ t → 0 ) .

Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.

Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.

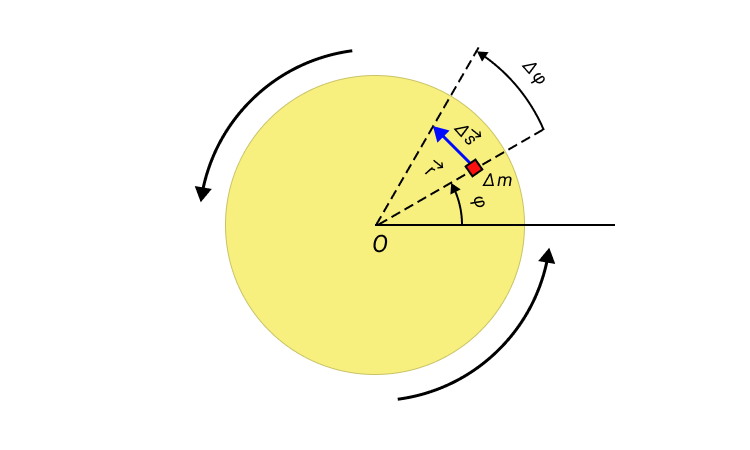
Рисунок 1. Вращение диска относительно оси, проходящей через его центр O .

Если угловое перемещение Δ φ мало, то модуль вектора линейного перемещения ∆ s → некоторого элемента массы Δ m вращающегося твердого тела можно выразить соотношением:

в котором r – модуль радиус-вектора r → .

Между модулями угловой и линейной скоростей можно установить связь посредством равенства

Модули линейного и углового ускорения также взаимосвязаны:

Векторы v → и a → = a τ → направлены по касательной к окружности радиуса r .

Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.

Модуль ускорения выражается формулой:

a n = v 2 r = ω 2 r .

Если разделить вращающееся тело на небольшие фрагменты Δ m i , обозначить расстояние до оси вращения через r i , а модули линейных скоростей через v i , то запись формулы кинестетической энергии вращающегося тела будет иметь вид:

E k = ∑ i ν m v i 2 2 = ∑ i ∆ m ( r i ω ) 2 2 = ω 2 2 ∑ i ∆ m i r i 2 .

Физическая величина ∑ i ∆ m i r i 2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:

I = ∑ i ∆ m i r i 2 .

В пределе при Δ m → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в С И – килограмм—метр в квадрате ( к г · м 2 ) . Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:

В отличие от выражения, которое мы использовали для описания кинестетической энергии поступательно движущегося тела m v 2 2 , вместо массы m в формулу входит момент инерции I . Также мы принимаем во внимание вместо линейной скорости v угловую скорость ω .

Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.

В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.

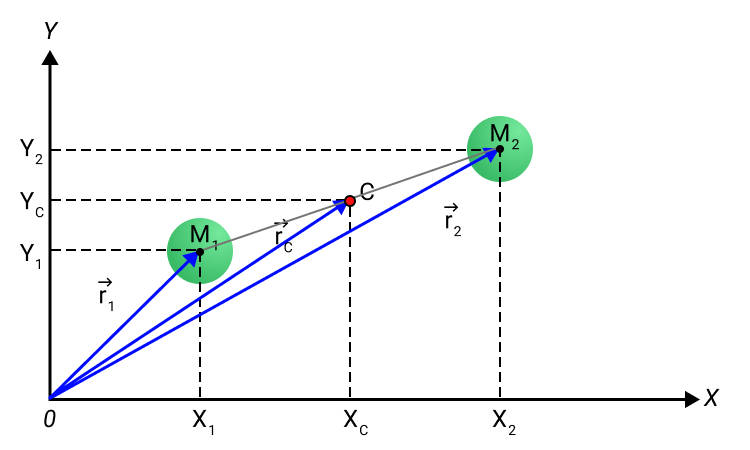
Положение x C , y C центра масс для простого случая системы из двух частиц с массами m 1 и m 2 , расположенными в плоскости X Y в точках с координатами x 1 , y 1 и x 2 , y 2 определяется выражениями:

x C = m 1 x 1 + m 2 x 2 m 1 + m 2 , y C = m 1 y 1 + m 2 y 2 m 1 + m 2 .

Рисунок 2. Центр масс C системы из двух частиц.

В векторной форме это соотношение принимает вид:

r C → = m 1 r 1 → + m 2 r 2 → m 1 + m 2 .

Аналогично, для системы из многих частиц радиус-вектор r C → центра масс определяется выражением

r C → = ∑ m i r i → ∑ m i .

Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для r C → необходимо заменить интегралами.

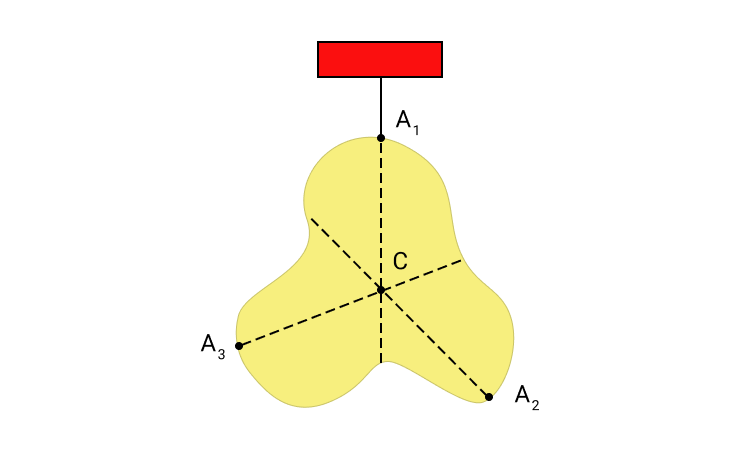
Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.

Рисунок 3. Определение положения центра масс C тела сложной формы. A 1 , A 2 , A 3 точки подвеса.

На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.

Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.

Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.

Теорема о движении центра масс

Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:

E k = m v C 2 2 + I C ω 2 2 ,

где m – полная масса тела, I C – момент инерции тела относительно оси, проходящей через центр масс.

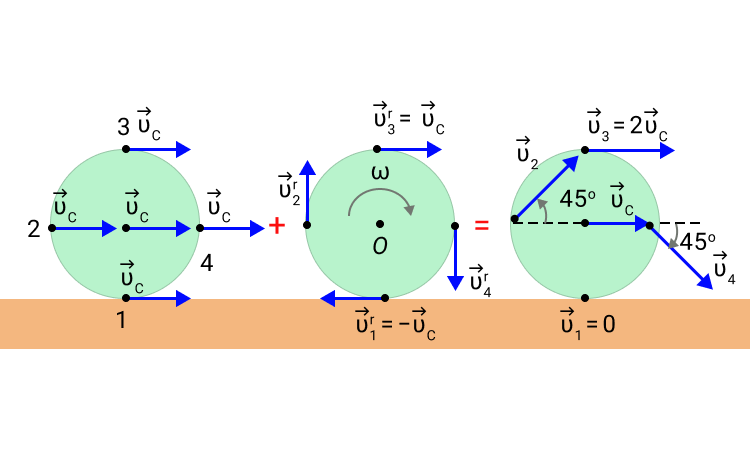
Рисунок 4. Качение колеса как сумма поступательного движения со скоростью v C → и вращения с угловой скоростью ω = v C R относительно оси O , проходящей через центр масс.

В механике используется теорема о движении центра масс.

Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.

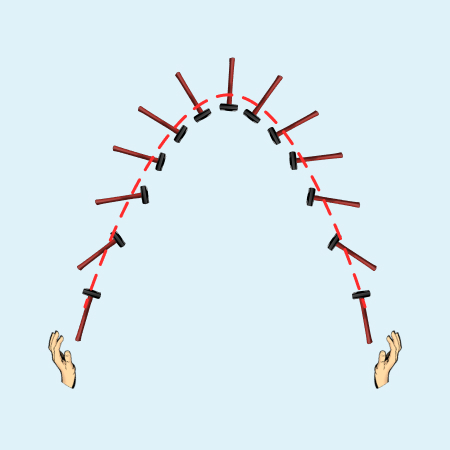
На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.

Рисунок 5. Движение твердого тела под действием силы тяжести.

Теорема Штейнера о параллельном переносе оси вращения

Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.

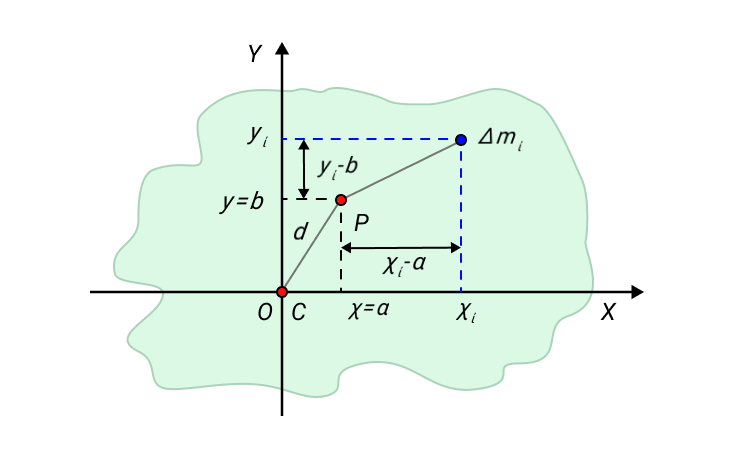
Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.

Для примера возьмем твердое тело, форма которого произвольна. Обозначим центр масс С . Выберем систему координат Х У с началом координат 0 . Совместим центр масс и начало координат.

Одна из осей проходит через центр масс С . Вторая ось пересекает произвольно выбранную точку Р , которая расположена на расстоянии d от начала координат. Выделим некоторый малый элемент массы данного твердого тела Δ m i .

По определению момента инерции:

I C = ∑ ∆ m i ( x i 2 + y i 2 ) , I P = ∑ m i ( x i — a ) 2 + y i — b 2

Выражение для I P можно переписать в виде:

I P = ∑ ∆ m i ( x i 2 + y i 2 ) + ∑ ∆ m i ( a 2 + b 2 ) — 2 a ∑ ∆ m i x i — 2 b ∑ ∆ m i y i .

Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.

Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.

Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

I P = I C + m d 2 ,

где m – полная масса тела.

Рисунок 7. Модель момента инерции.

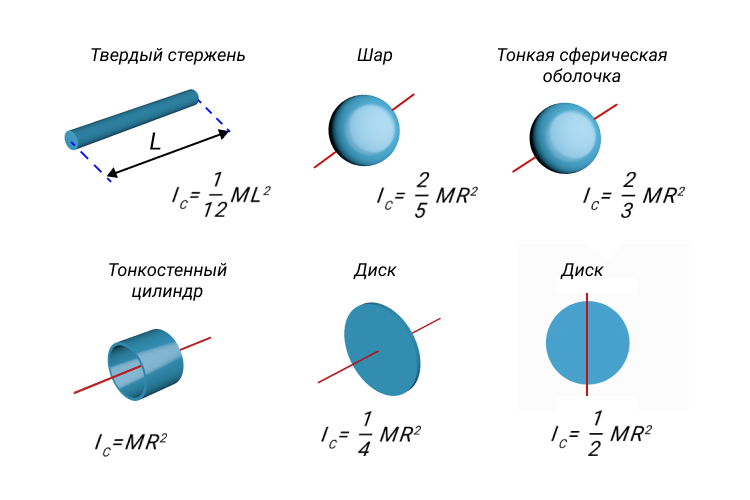
На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.

Рисунок 8. Моменты инерции I C некоторых однородных твердых тел.

Основное уравнение динамики вращательного движения твердого тела

В тех случаях, когда мы имеем дело с твердым телом, которое вращается относительно неподвижной оси, мы можем обобщить второй закон Ньютона. На рисунке ниже мы изобразили твердое тело произвольной формы, вращающееся относительно некоторой оси, проходящей через точку О . Ось вращения расположена перпендикулярно плоскости рисунка.

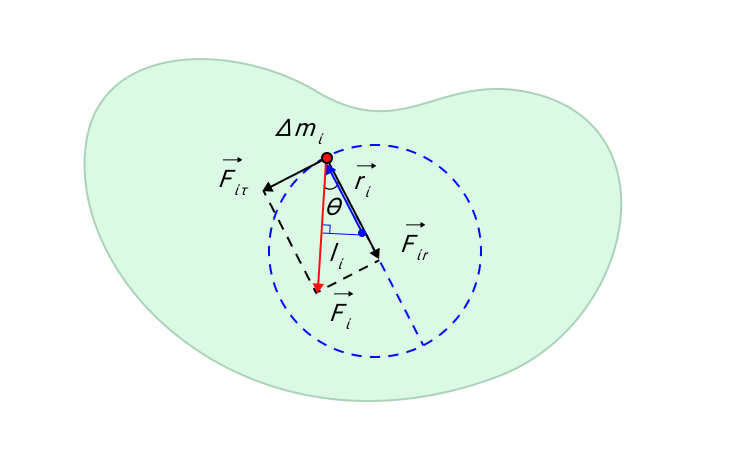
Δ m i – это произвольный малый элемент массы, на который оказывают воздействие внешние и внутренние силы. Равнодействующая всех сил есть F i → . Ее можно разложить на две составляющие: касательную составляющую F i τ → и радиальную F i r → . Радиальная составляющая F i r → создает центростремительное ускорение a n .

Рисунок 9. Касательная F i τ → и радиальная F i r → составляющие силы F i → действующей на элемент Δ m i твердого тела.

Касательная составляющая F i τ → вызывает тангенциальное ускорение a i τ → массы Δ m i . Второй закон Ньютона, записанный в скалярной форме, дает

∆ m i a i τ = F i τ sin θ или ∆ m i r i ε = F i sin θ ,

где ε = a i τ r i – угловое ускорение всех точек твердого тела.

Если обе части написанного выше уравнения умножить на r i , то мы получим:

∆ m i r i 2 ε = F i r i sin θ = F i l i = M i .

Здесь l i – плечо силы, F i , → M i – момент силы.

Теперь нужно аналогичные соотношения записать для всех элементов массы Δm_i вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:

∑ ∆ m i r i 2 ε = ∑ M i .

Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.

∑ M = ∑ M i в н е ш н + ∑ M i в н у т р .

Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M . Так мы получили основное уравнение динамики вращательного движения твердого тела.

Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.

Обычно за положительное направление вращения принимают направление против часовой стрелки.

Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины ω → , ε → , M → определяются как векторы, направленные по оси вращения.

Закон сохранения момента импульса

В разделе, посвященном поступательному движению тела, мы ввели понятие импульса тела p → . По аналогии с поступательным движением для вращательного движения мы вводим понятие момента импульса.

Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.

Для обозначения момента импульса используется латинская буква L .

Поскольку ε = ∆ ω ∆ t ; ∆ t → 0 , уравнение вращательного движения можно представить в виде:

M = I ε = I ∆ ω ∆ t или M ∆ t = I ∆ ω = ∆ L .

M = ∆ L ∆ t ; ( ∆ t → 0 ) .

Мы получили это уравнение для случая, когда I = c o n s t . Но оно будет справедливо и тогда, когда момент инерции тела будет изменяться в процессе движения.

Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = I ω относительно данной оси сохраняется: ∆ L = 0 , если M = 0 .

L = l ω = c o n s t .

Так мы пришли к закону сохранения момента импульса.

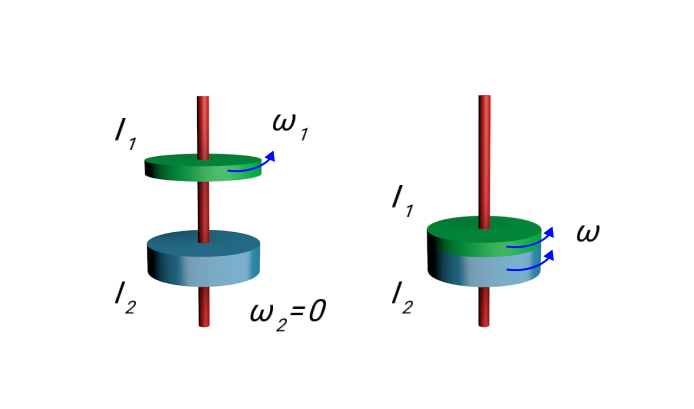
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.

Рисунок 10. Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I 1 ω 1 = ( I 1 + I 2 ) ω .

Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.

Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.

Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.

Рисунок 11. Качение симметричного тела по наклонной плоскости.

Ось вращения O проходит через центр масс тела. Моменты силы тяжести m g → и силы реакции N → относительно оси O равны нулю. Момент M создает только сила трения: M = F т р R .

Уравнение вращательного движения:

I C ε = I C a R = M = F т р R ,

где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, I C – момент инерции относительно оси O , проходящей через центр масс.

Второй закон Ньютона для поступательного движения центра масс записывается в виде:

m a = m g sin α — F т р .

Исключая из этих уравнений F т р , получим окончательно:

α = m g sin θ I C R 2 + m .

Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара I C = 2 5 m R 2 , а у сплошного однородного цилиндра I C = 1 2 m R 2 . Следовательно, шар будет скатываться быстрее цилиндра.