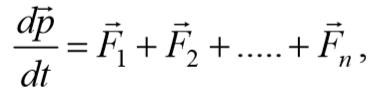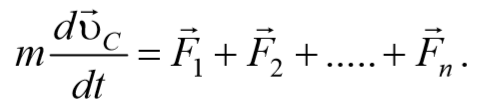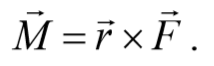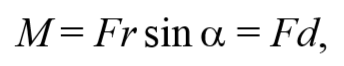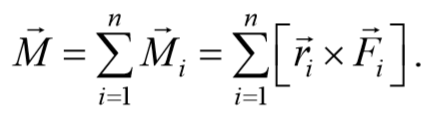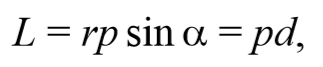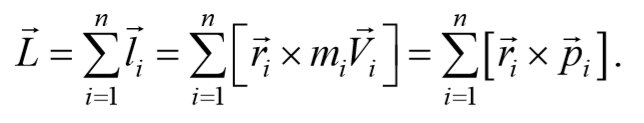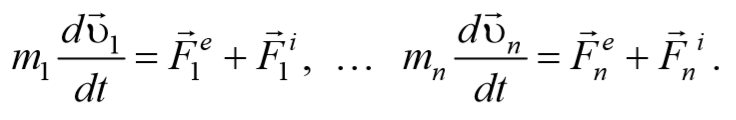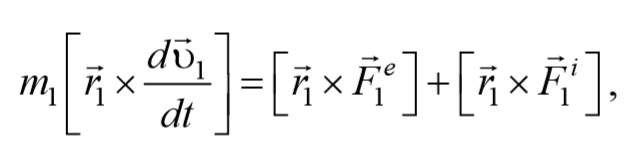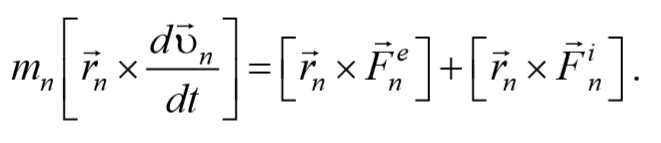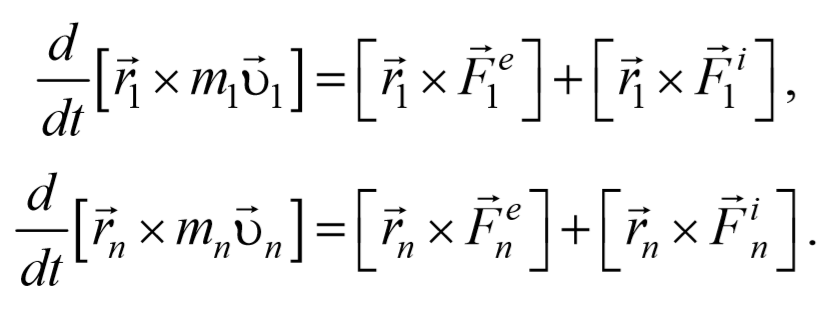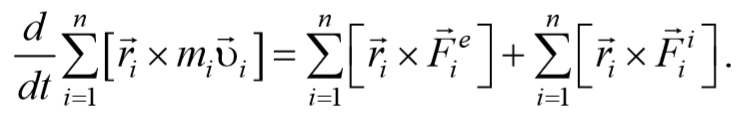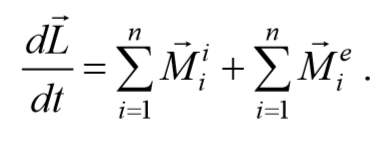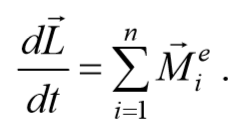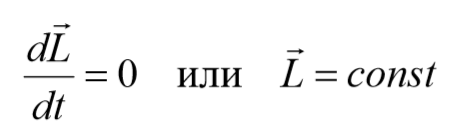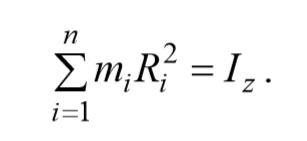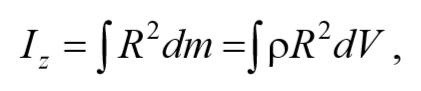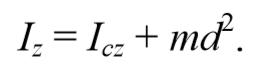Лекция №5. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
4.1. Динамика поступательного движения твердого тела.
Движение любого твердого тела можно рассматривать как сумму поступательного движения его центра масс и вращательного движения относительно оси, проходящей через его центр масс.
Разобьем твердое тело на элементарные массы mi , тогда его можно представить как систему материальных точек, взаимное расположение которых остается неизменным. Поэтому для описания поступательного движения тела можно использовать закон изменения импульса механической системы
p = $$<\sum_
Также можно воспользоваться понятием центра масс и к поступательному движению твердого тела применить закон движения центра масс
Центр масс твердого тела движется как материальная точка, в которой сосредоточена масса тела, и на которую действуют все силы, приложенные к телу. Уравнение (4.1.2) дает возможность установить закон движение центра масс твердого тела, если известна масса тела и действующие на него силы. Если тело движется только поступательно, то это уравнение будет определять не только закон движения центра масс, но и любой другой точки тела.
4.2. Момент импульса. Момент силы.
Момент силы. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенному из полюса в точку приложения силы, на силу F называется моментом силы материальнойточки относительно некоторого центра
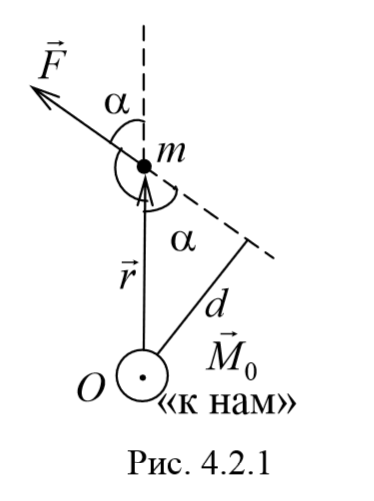
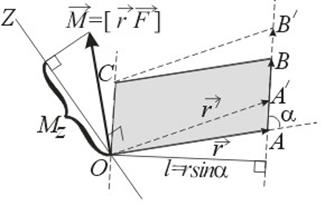
Пусть на частицу массой m действует сила F , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент силы частицы относительно точки O дается уравнением (4.2.1). Направление момента силы M совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора r к силе F , и он перпендикулярен как вектору r , так и вектору F (рис. 4.2.1). Тогда модуль вектора момента силы равен
где d=r sin α − плечо силы относительно точки O .
Плечо силы − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой действует сила.
Таким образом, модуль момента силы относительно оси, есть скалярная величина, характеризующая вращательное движение действия силы и равная произведению модуля силы F , действующей на твердое тело, на плечо силы d относительно этой оси.
Если на тело действует несколько сил, то суммарный момент этих сил равен векторной сумме моментов всех сил относительно данной оси:
Момент импульса. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенного из центра на ее импульс m υ называется моментом импульса материальной точки относительно некоторого центра
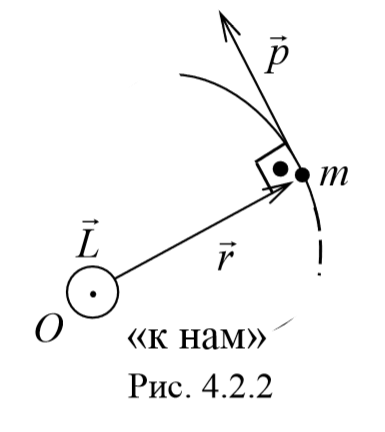
Пусть частица массой m имеет импульс p , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент импульса частицы относительно точки O дается уравнением (4.2.4). Направление момента импульса совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к импульсу p , и он перпендикулярен как вектору r , так и вектору p (рис. 4.2.2). Тогда модуль вектора момента импульса равен
где d − плечо импульса относительно точки O .
Плечо импульса − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой направлен импульс.
Таким образом, модуль вектора момента импульса относительно центра или оси − есть скалярная величина, равная произведению импульса p на плечо импульса d относительно этой оси.
Моментом импульса механической системы относительно некоторого центра называется векторная величина, равная геометрической сумме моментов импульса относительно той же точки всех материальных точек системы
4.3. Основное уравнение динамики вращательного движения относительно точки.
Рассмотрим систему материальных точек массами m1, m2, . mn движущихся со скоростями υ 1, υ 2, . υ n . Пусть на каждую из этих точек действуют: равнодействующие внутренних сил F i 1, F i 2, . F i n , и равнодействующие внешних сил F e 1, F e 2, . F e n .
Запишем уравнения движения частиц:
Умножим каждое уравнение системы (4.3.3) на соответствующий радиус-вектор и получим
Преобразуем данные уравнения
Сложим эти уравнения и получим
В последнем уравнении:
Таким образом, выражение (4.3.6) можно записать в виде
Учитывая, что моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы всегда равна нулю, т. е. $$<\sum_
4.4. Закон сохранения момента импульса.
Если момент внешних сил $$<\sum_
закон сохранения момента импульса.
Если момент внешних сил действующих на механическую систему относительно центра оси равен нулю, то момент импульса системы относительно этого центра с течением времени не изменяется.
Можно сказать, что момент силы при вращательном движении является аналогом силы при поступательном движении, момент импульса − аналогом импульса.
Законы изменения и сохранения момента импульса механической системы можно применить и к вращательному движению твердого тела.
4.5. Момент инерции.
Моментом инерции твердого тела относительно данной оси называется физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси:
Момент инерции зависит только от формы тела и расположения масс относительно оси. [I]=1 кг · м 2 .
Понятие момента инерции было введено при рассмотрении вращения твердого тела. Однако следует иметь в виду, что каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси.
Если тело сплошное, то суммирование в выражении (4.5.1) следует заменить на интегрирование:
где R − расстояние от элементарной массы dm до оси вращения.
4.6. Теорема Штейнера. Правило аддитивности
Существуют два свойства момента инерции:
1) Теорема Штейнера: момент инерции тела Iz относительно произвольной оси равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:
2) Правило аддитивности: сумма моментов инерции частей системы относительно оси равен моменту инерции системы относительно данной оси:
Уравнение моментов: моменты силы, импульса и инерции
Если линейное перемещение тел описывают в классической механике с помощью законов Ньютона, то характеристики движения механических систем по круговым траекториям вычисляют с помощью специального выражения, которое называется уравнением моментов. О каких моментах идет речь и в чем заключается смысл этого уравнения? Эти и другие вопросы раскрываются в статье.
Момент силы
Всем хорошо известна ньютоновская сила, которая, действуя на тело, приводит к сообщению ему ускорения. Когда же такая сила прилагается к объекту, который закреплен на некоторой оси вращения, то эту характеристику принято называть моментом силы. Уравнение момента силы может быть записано в следующем виде:

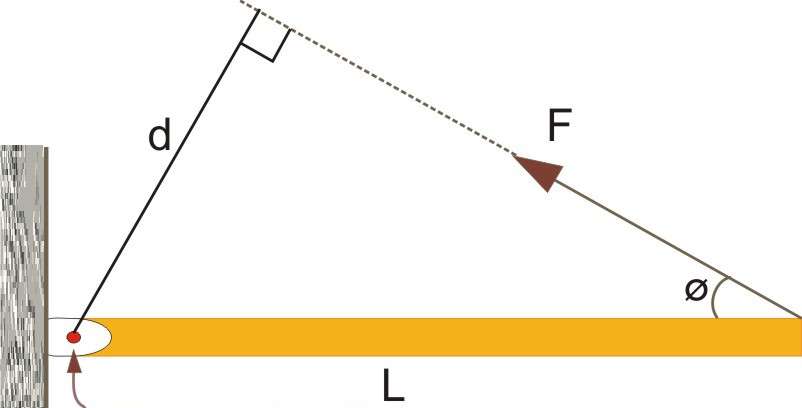
Рисунок, поясняющий это выражение, приведен ниже.
Здесь видно, что сила F¯ направлена к вектору L¯ под углом Φ. Сам же вектор L¯ полагается направленным от оси вращения (указана стрелкой) к точке приложения F¯.

Приведенная выше формула представляет собой произведение двух векторов, поэтому величина M¯ также является направленной. Куда будет повернут момент силы M¯? Это можно определить по правилу правой руки (четыре пальца направлены вдоль траектории от конца вектора L¯ к концу F¯, а отставленный палец большой показывает направление M¯).
На рисунке выше выражение для момента силы в скалярном виде примет форму:
Если внимательно всмотреться в рисунок, то можно увидеть, что L*sin(Φ) = d, тогда имеем формулу:
Величина d является важной характеристикой при вычислении момента силы, поскольку она отражает эффективность приложенной F к системе. Эту величину принято называть рычагом силы.
Физический смысл M заключается в способности силы совершить вращение системы. Эту способность может ощутить на себе каждый, если будет открывать дверь за ручку, толкая ее около петель, или же попробует открутить гайку коротким и длинным ключом.
Равновесие системы
Понятие о моменте силы оказывается очень полезным, когда рассматривают равновесие системы, на которую действуют несколько сил, и которая имеет ось или точку вращения. В таких случаях применяют формулу:
То есть система будет находиться в равновесии, если сумма всех моментов сил, приложенных к ней, нулевая. Заметим, что в этой формуле присутствует знак вектора над моментом, то есть при решении следует не забывать учитывать знак этой величины. Общепринятым правилом считается, что действующая сила, которая вращает систему против часовой стрелки, создает положительный Mi¯.
Ярким примером задач рассматриваемого типа являются проблемы с равновесием рычагов Архимеда.
Момент импульса
Это еще одна важная характеристика движения по окружности. В физике ее описывают произведением количества движения на рычаг. Уравнение момента импульса имеет такой вид:
Здесь p¯ — вектор импульса, r¯ — вектор, соединяющий вращающуюся материальную точку с осью.
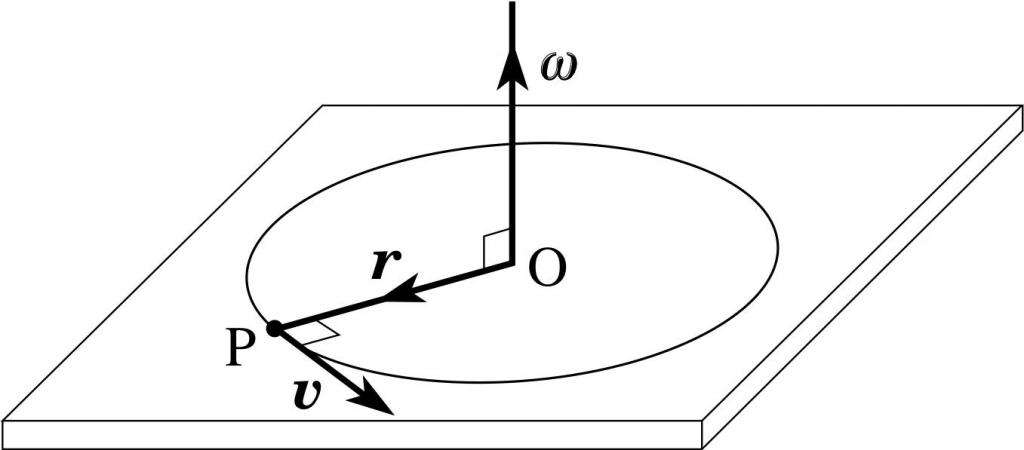
Поясняющий это выражение рисунок приведен ниже.
Здесь ω — угловая скорость, которая дальше появится в уравнении моментов. Заметим, что направление вектора T¯ находится по тому же правилу, что и M¯. На рисунке выше T¯ по направлению будет совпадать с вектором угловой скорости ω¯.
Физический смысл величины T¯ является таким же, как и характеристики p¯ в случае линейного движения, то есть момент импульса описывает количество вращательного движения (запасенную кинетическую энергию).
Момент инерции
Третья важная характеристика, без которой невозможно составить уравнение движения вращающегося объекта, — это момент инерции. Появляется он в физике в результате математических преобразований формулы для момента импульса материальной точки. Покажем, как это делается.
Представим величину T¯ в следующем виде:
T¯ = r¯*m*v¯, где p¯ = m*v¯
Пользуясь связью между угловой и линейной скоростями, можно переписать это выражение следующим образом:
T¯ = r¯*m*r¯*ω¯, где v¯ = r¯*ω¯
Последнее выражение запишем в виде:
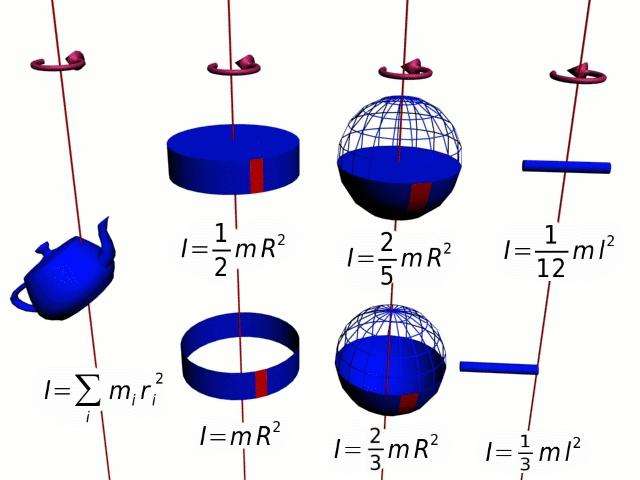
Величина r2*m — это момент инерции I для точки массой m, которая совершает круговое движение вокруг оси на расстоянии от нее r. Этот частный случай позволяет ввести общее уравнение момента инерции для тела произвольной формы:
I — это аддитивная величина, смысл которой заключается в инерционности вращающейся системы. Чем больше I, тем труднее раскрутить тело, и необходимо приложить значительные усилия, чтобы его остановить.
Уравнение моментов
Мы рассмотрели три величины, название которых начинается со слова «момент». Это сделано было намеренно, поскольку все они связаны в одно выражение, получившее название уравнения 3 моментов. Выведем его.
Рассмотрим выражение для момента импульса T¯:
Найдем, как изменяется величина T¯ во времени, имеем:
Учитывая, что производная угловой скорости равна таковой для скорости линейной, деленной на r, а также раскрывая величину I, приходим к выражению:
dT¯/dt = m*r2*1/r*dv¯/dt = r*m*a¯, где a¯ = dv¯/dt — линейное ускорение.
Заметим, что произведение массы на ускорение — это не что иное, как действующая внешняя сила F¯. В итоге получаем:
Мы пришли к интересному выводу: изменение момента импульса равно моменту действующей внешней силы. Это выражение принято записывать в несколько иной форме:
M¯ = I*α¯, где α¯ = dω¯/dt — угловое ускорение.
Это равенство называется уравнением моментов. Оно позволяет рассчитать любую характеристику вращающегося тела, зная параметры системы и величину внешнего воздействия на нее.
Закон сохранения T¯
Полученный в предыдущем пункте вывод свидетельствует о том, что если внешний момент сил будет равен нулю, то момент импульса меняться не будет. В таком случае запишем выражение:
T¯ = const. или I1*ω1¯ = I2*ω2¯
Эта формула носит название закона сохранения величины T¯. То есть любые изменения внутри системы суммарный момент импульса не меняют.
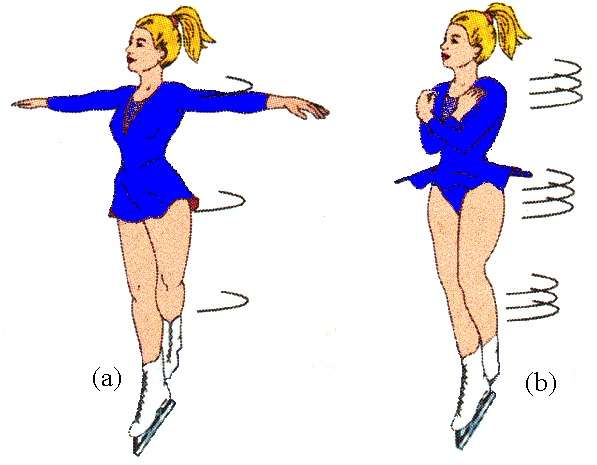
Этот факт используется фигуристами и балеринами во время их выступлений. Также его применяют, если необходимо выполнить поворот вокруг своей оси искусственного спутника, движущегося в космосе.
Момент силы и момент импульса.
Вращение является составляющей большинства рассматриваемых в механике движений. Каждый день мы являемся свидетелями великого космического вращения. Данные последних теоретических исследований говорят, что всё вокруг и мы сами по свойствам напоминаем вращающиеся с большой частотой поля.
Динамические характеристики – момент силы и момент импульса, используемые при описании вращательного движения, играют в теории вращательного движения такую же большую роль, какую сила и импульс играют в динамике поступательного движения.
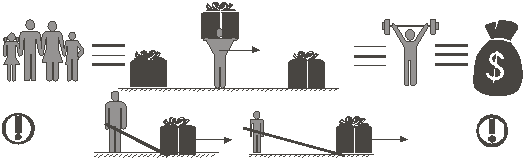
Известно, что передвинуть массивный предмет (например, ящик) вручную тяжело, гораздо легче передвинуть его с помощью длинной палки, трубы (лома), т.е. перекантовать с помощью рычага, причем, чем длинней этот рычаг, тем легче это сделать (прикладывается меньшая сила при большей длине рычага (см. рис. 4.8)). Вспомним знаменитое изречение Архимеда (ок. 286–212 гг. до н.э.): «Дайте мне точку опоры (и рычаг) и я переверну Землю».
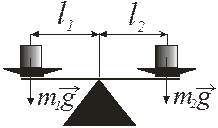
Другой пример – взвешивание предметов на весах (см. рис. 4.9): при равных плечах (силы) весов li перевесит тот груз, масса которого mi больше, а если массы грузов равны, то перевесит груз, для которого плечо силы li больше.
Следует различать момент силы и момент импульса относительно точки и относительно оси, в первом случае – это вектора, а во втором – проекции векторов (скаляры).
Пусть дана точка О (полюс), относительно которой находится момент силы. Моментом силы 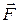
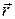
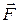
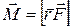
Модуль момента силы:
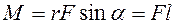
где l=rsina – кратчайшее расстояние до линии АВ действия силы (рис.4.10), называемое плечом силы l.
При этом вектор 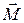
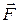
В отличие от полярных векторов 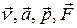
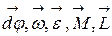
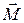
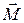
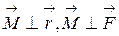
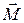
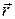
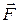
Главным моментом 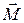
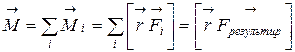
где силы 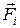
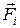
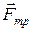
При вращении ТТ (системы материальных точек) необходимо учитывать только внешние силы,так как внутренние силы взаимодействия двух любых элементов ТТ (системы) всегда равны по модулю (величине) и противонаправлены вдоль одной прямой (их векторная (геометрическая) сумма равна нулю).
Аналогично вышесказанному можно определить момент импульса относительно точки (вектор 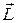
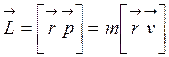
где 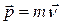
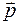
Единицы измерения[М]=Н×м (не путать с [А]=Дж=Н×м), а 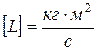
В общем случае 
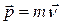
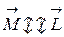
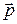
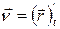
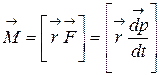
т.к. 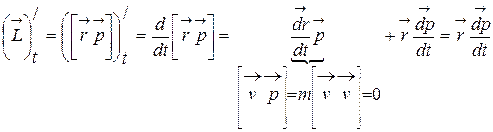
то есть получают основное уравнение динамики вращательного движения:
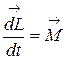
Этот закон остается справедливым и для системы материальных точек, в этом случае
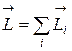
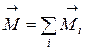
Особенность вращения ТТ, по сравнению с системой несвязанных друг с другом материальных точек, заключается в том, что при вращении ТТ вокруг неподвижной оси все его элементы движутся по окружностям, причем угловая скорость вращения 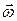
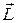
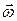
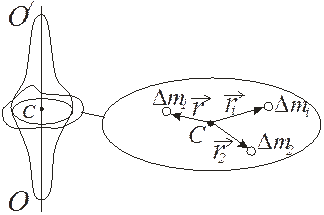
Разобьем ТТ (рис. 4.11), вращающееся относительно оси ОО / , на элементы (материальные точки). Момент импульса каждого элемента
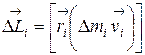
С учетом равенства
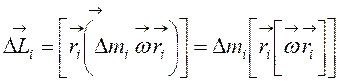
В математике известно, что двойное векторное произведение имеет вид
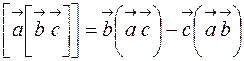
т.е. 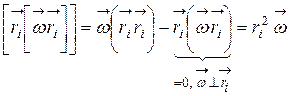
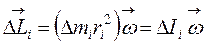
где DIi – момент инерции i–го элемента.
Суммируя (интегрируя) по всем элементам, получают:

С учетом формул (4.20) и (4.23) получаем еще одну форму записи основного уравнения динамики вращательного движения:
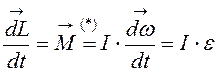
где e – угловое ускорение.
При вращении ТТ (системы материальных точек) необходимо учитывать только внешние силы,так как внутренние силы взаимодействия двух любых элементов ТТ (системы) всегда равны по модулю (величине) и противонаправлены вдоль одной прямой (их векторная (геометрическая) сумма равна нулю). Согласно уравнению (4.21) для замкнутой системы имеем:
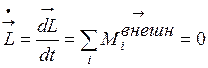
т.е. 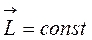
Значит,для замкнутых систем выполняется закон сохранения момента импульса.
http://1ku.ru/obrazovanie/28956-uravnenie-momentov-momenty-sily-impulsa-i-inercii/
http://helpiks.org/3-35417.html