Уравнение моментов относительно неподвижной точки и оси

Уравнение моментов

Определение и уравнение моментов

Пусть O — любая неподвижная точка в инерциальной системе отсчета. Это называется началом или полюсом. Обозначим через радиус-вектор, взятый от этой точки до точки приложения силы (рис.1).

Момент силы относительно точки O является векторным произведением радиус-вектора и силы :

направление выбрано так, что последовательность векторов образует правую систему, т. е. если вы посмотрите вдоль вектора ,то поворот вдоль кратчайшего пути от первого фактора в (1) до вторая выполняется по часовой стрелке, таким образом совпадает с направлением поступательного движения правого штыря, ручка которого вращается от до вдоль кратчайшего пути.

Моментом нескольких сил относительно точки является векторная сумма моментов этих сил относительно одной и той же точки:

Момент импульса материальной точки

Момент импульса материальной точки относительно точки O является векторным произведением радиус-вектора и импульса

где J — момент инерции, — угловая скорость вращения тела.

Система из n материальных точек — это момент количества движения относительно некоторой точки O — векторная сумма моментов импульсов этих точек относительно того же начала:

Временная производная от момента импульса механической системы относительно неподвижной точки (полюса О) равна сумме внешних силовых моментов , действующих на систему:

Для материальной точки уравнение момента написано:

Уравнение (6) называется моментом для системы материальных точек. Это основной закон динамики твердого тела, вращающегося вокруг неподвижной точки.

В проекциях на оси фиксированной декартовой системы координат с началом на полюсе O уравнение моментов системы записывается в виде:

где — проекция момента количества движения на соответствующей оси; — проекции полного момента сил на соответствующую ось.

Уравнение моментов позволяет получить ответ на следующие вопросы:

1. найти момент силы (общий момент внешних сил) относительно интересующей нас точки в любой момент времени, если известна зависимость момента количества движения частицы (системы частиц) от одной и той же точки;

2. определить приращение углового момента частицы (системы частиц) относительно точки O для любого периода времени, если временная зависимость силового момента (полного момента внешних сил), действующего на эту частицу (система частиц) относительно одной и той же точки.

Примеры решения проблем

Сравните угловые скорости, полученные материальной точкой под действием крутящих моментов, графики (a, b) которых показаны на рисунках.

В соответствии с уравнением моментов для материальной точки мы имеем:

поскольку мы имеем дело с материальной точкой, соответственно, J не зависит от времени, получаем:

Вспомните геометрический смысл интеграла.

Вычислить и сравнить площадь треугольников OAB и OCD.

Области треугольников равны соответственно

Угловые скорости, полученные материальной точкой, равны в первом и втором случаях.

Горизонтальный диск с радиусом R = 0,2 м и массой m = 5 кг вращается вокруг оси, проходящей через ее центр. Зависимость угловой скорости вращения диска от времени определяется уравнением w = A + 8t. Найдите значение касательной силы, приложенной к ободу диска. Трение пренебрегалось.

Мы делаем рисунок

Запишем уравнение моментов:

где — искомая сила. Перепишите (2.2), найдите модуль: — угол между вектором и равен , так как силы, касательные к диску, направлены вдоль радиуса диска в точку касания, следовательно, M = RF.

Поскольку мы имеем дело с телом, который не меняет момент инерции со временем, мы имеем:

Где — момент инерции диска относительно оси, проходящей через его центр.

Подставим числовые значения, получим:

Величина (модуль) касательной силы, приложенной к краю диска, равна 4 N.

Электронная библиотека

Моментом импульса материальной точки относительно неподвижной точки ( ) называется физическая величина, определяемая векторным произведением:

где -радиус-вектор, проведенный из точки О в точку А; — импульс материальной точки (рис. 4.4); – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

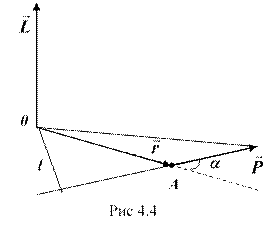
Модуль вектора момента импульса равен:

где – угол между векторами и ; – плечо вектора относительно точки O.

Моментом импульса относительно неподвижной оси (z) называется скалярная величина ( ), равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки (О) данной оси. Момент импульса ( ) не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса с некоторой скоростью . Скорость и импульс перпендикулярны этому радиусу, то есть радиус является плечом вектора . Поэтому можем записать, что момент импульса отдельной частицы равен: и направлен по оси в сторону, определяемую правилом правого винта.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.

Продифференцировав уравнение (4.1) по времени получим:

Это выражение есть еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. Физический смысл этого выражения: скорость изменения момента импульса равна моменту сил.

В векторной форме это можно записать так:

В замкнутой системе момент ( ) внешних сил равен нулю и, следовательно, , откуда

Выражение (4.2) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы не изменяется с течением времени. Закон сохранения момента импульса – фундаментальный закон природы.

Он связан со свойством симметрии пространства – его изотропностью, то есть с инвариантностью физических законов относительно выбора направления осей координат системы отсчета. Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение: