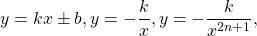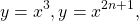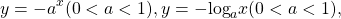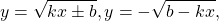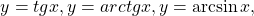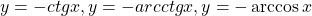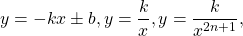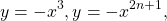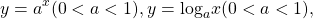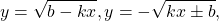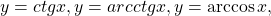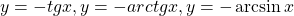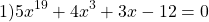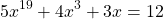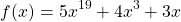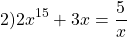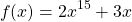Уравнение на монотонность 9 класс

Решение уравнений с помощью монотонности функций

Решение уравнений с помощью монотонности функций позволяет быстро и просто найти корень уравнения (либо доказать, что уравнение корней не имеет).

Использование возрастания и убывания функций при решении уравнений опирается на следующие теоремы.

1) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)).

2) Если на некотором промежутке функция f(x) возрастает, а функция g(x) убывает (либо наоборот), то уравнение f(x)=g(x) на этом промежутке имеет единственный корень либо не имеет корней.

Доказав, что уравнение имеет на промежутке не более чем один корень, можно попытаться определить его подбором.

Если функция имеет несколько промежутков возрастания и убывания, каждый из них следует рассмотреть отдельно.

Сумма возрастающих функций — возрастающая функция. Сумма убывающих функций — убывающая функция.

Прибавление или вычитание постоянной величины не влияет на монотонность функции. Если к возрастающей функции прибавить (или вычесть) постоянную величину, получим возрастающую функцию. Если к убывающей функции прибавить (или вычесть) постоянную величину, получим убывающую функцию.

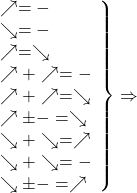
Таким образом, использование монотонности функций при решении уравнений схематически можно изобразить так:

то уравнение имеет единственный корень или не имеет корней.

Разумеется, количество слагаемых может быть больше двух.

Некоторые функции, возрастающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения (k>0, b≥0, n — целое):

1),y = <\log _a>x(a > 1),\]» title=»Rendered by QuickLaTeX.com»/>

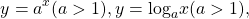
Некоторые функции, убывающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения:

1),y = — <\log _a>x(a > 1),\]» title=»Rendered by QuickLaTeX.com»/>

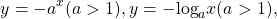
Примеры решения уравнений с помощью использования монотонности функций.

Перепишем уравнение в виде

является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.

На промежутке (-∞;0) функция

— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x= -1.

Аналогично, на промежутке (0:∞)

— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x=1.

В алгебре решение уравнений с применением возрастания и убывания функций чаше всего используется при решении иррациональных, логарифмических, показательных уравнений. Полезно взять на вооружение этот удобный и быстрый способ.

2 комментария

Добрый день. Вот это схематическое изображение монотонности очень интересно, но там не все понятно. Что вы подразумеваете под знаками равно и минус? И вот это: сумма убывающих_возрастающая? Буду благодарна комментариям

Елена, «=» — знак равенства между левой и правой частями уравнения.
Сумма убывающих функций — убывающая функция. Соответственно, одна часть уравнения — убывающая функция, а другая — возрастающая, то применима вторая теорема.
Аналогично, сумма возрастающих функций есть возрастающая функция. Если с одной стороны — возрастающая функция, с другой — убывающая, можем применить первую теорему.
Если к монотонно возрастающей функции прибавить число (или вычесть), то это никак не повлияет на её монотонность (это наглядно можно продемонстрировать графически: график функции y=f(x)±b получен из графика y=f(x) параллельным переносом на b единиц вверх или вниз вдоль оси Oy). Поэтому, если в одной части уравнения — монотонно возрастающая функция ± число, а в другой — монотонно убывающая функция, можем применить теорему два. И т.д.

Монотонность функций. Исследование функций на монотонность. — презентация

Презентация была опубликована 9 лет назад пользователемfestival.1september.ru

Похожие презентации

Презентация 9 класса на тему: «Монотонность функций. Исследование функций на монотонность.». Скачать бесплатно и без регистрации. — Транскрипт:

1 Материал по теме «Монотонность функций» подготовлен учениками 9 класса подготовлен учениками 9 класса Исследование функций на монотонность.

2 План показа: Введение. Введение. 1. Определения возрастающей и убывающей функций. Графики функций. 1. Определения возрастающей и убывающей функций. Графики функций. 2.Алгоритм исследования функции на монотонность. 2.Алгоритм исследования функции на монотонность. 3. Примеры исследования функций на монотонность. 3. Примеры исследования функций на монотонность. Выводы. Выводы.

3 Введение. Введение. Только с алгеброй начинается строгое математическое учение. Только с алгеброй начинается строгое математическое учение. Н.И. Лобачевский Н.И. Лобачевский Мы изучаем алгебру по комплектам учебников (под рук. Мордковича А.Г.), где учебный материал излагается по схеме: Мы изучаем алгебру по комплектам учебников (под рук. Мордковича А.Г.), где учебный материал излагается по схеме: функция — уравнения – преобразования. функция — уравнения – преобразования. В 7-м и 8-м классах мы учились читать графики, описывая некоторые свойства функций. В 7-м и 8-м классах мы учились читать графики, описывая некоторые свойства функций. В 9-м классе узнали много новых определений и научились применять их для исследования функций. Таким образом, появилась возможность, ответить на многие вопросы без построения графиков функций и, наоборот, по графикам – определить свойства функций. В 9-м классе узнали много новых определений и научились применять их для исследования функций. Таким образом, появилась возможность, ответить на многие вопросы без построения графиков функций и, наоборот, по графикам – определить свойства функций. Замечательным свойством функции является монотонность. Наш показ посвящен этому свойству. Замечательным свойством функции является монотонность. Наш показ посвящен этому свойству.

4 1.Определения возрастающей и убывающей функций. Функцию y = f(x) называют возрастающей на множестве X D(f), если для любых двух точек x 1 и x 2 множества X, таких, что x 1

5 3. Алгоритм исследования функции на монотонность. 1. Найти область определения функции y = f(x): множество X D(f). 2. Выбрать произвольные значения аргумента x 1 и x 2 множества X такие, что x 1

6 4. Примеры исследования функций на монотонность. Исследовать на монотонность функцию: Исследовать на монотонность функцию: 1. y = 2 — 5x; 1. y = 2 — 5x; 2. y = x 3 +4; 2. y = x 3 +4; 3. y = x 3 +2x 2 ; 3. y = x 3 +2x 2 ; 4. y = — 3x 3 — x; 4. y = — 3x 3 — x; 5. y = x 0,5 +x 5 ; 5. y = x 0,5 +x 5 ; 6. y = — x 3 — x 0,5. 6. y = — x 3 — x 0,5.

7 1. y = 2 – 5x. Решение. Решение. 1. Область определения функции y = 2 – 5x: D(y)= (- ; + ). 2. Выберем произвольные значения аргумента x 1 и x 2 из D(y) такие, что x 1 – x 2 ; 2 – 5 x 1 > 2 – 5 x Итак, из x 1 f (x 2 ), то заданная функция убывает на D(y). – x 2 ; 2 – 5 x 1 > 2 – 5 x 2 3. 5. Итак, из x 1 f (x 2 ), то заданная функция убывает на D(y).»>

8 2. y = x y = x Решение. Решение. 1. Область определения функции y = x : D(y)= (- ; + ). 2. Выберем произвольные значения аргумента x 1 и x 2 из D(y) такие, что x 1

9 3. y = x 3 +2x 2. Решение. Решение. Область определения функции y = x 3 + 2x 2 : D(y)= (- ; + ). Область определения функции y = x 3 + 2x 2 : D(y)= (- ; + ). Выберем произвольные значения аргумента x 1 и x 2 из D(y) такие, что x 1

10 4. y = – 3x 3 – x. Решение. Решение. 1. Область определения функции y = – 3x 3 – x : D(y)= (- ; + ). 2. Выберем произвольные значения аргумента x 1 и x 2 из D(y) такие, что x 1 – x 2 3 ; – x 1 (3x ) > – x 2 (3x ); – 3x 1 3 – x 1 > – 3x 2 3 – x Итак, из x 1 f (x 2 ), то заданная функция убывает на D(y). – x 2 3 ; – x 1 (3x 1 2 + 1) > – x 2 (3x 2 2 +1); – 3x 1 3 – x 1 > – 3x 2 3 – x 2. 5. Итак, из x 1 f (x 2 ), то заданная функция убывает на D(y).»>

11 5. y = x 0,5 +x 5. Решение. Решение. 1. Область определения функции y = x 0,5 +x 5 : D(y)= [ 0 ; + ). 2. Выберем произвольные значения аргумента x 1 и x 2 из D(y) такие, что x 1

12 6. y = — x 3 — x 0,5. Решение. Решение. 1. Область определения функции y = – x 3 – x 0,5 : D(y)= [ 0; + ). 2. Выберем произвольные значения аргумента x 1 и x 2 из D(y) такие, что x 1 – x 2 3 ; – x 1 0,5 > – x 2 0,5 ; –x 1 0,5 (x 1 2,5 + 1) > – x 2 (x 2 2,5 +1); – x 1 3 – x 1 0,5 > – x 2 3 – x 2 0,5. 5. Итак, из x 1 f (x 2 ), то заданная функция убывает на D(y). – x 2 3 ; – x 1 0,5 > – x 2 0,5 ; –x 1 0,5 (x 1 2,5 + 1) > – x 2 (x 2 2,5 +1); – x 1 3 – x 1 0,5 > – x 2 3 – x 2 0,5. 5. Итак, из x 1 f (x 2 ), то заданная функция убывает на D(y).»>

13 Выводы. Выводы. Данный материал подготовлен как вводное повторение для урока по теме « Теорема о корне при решении уравнений». Данный материал подготовлен как вводное повторение для урока по теме « Теорема о корне при решении уравнений». Свойство монотонности функции будет в дальнейшем использоваться для решения нестандартных задач. Свойство монотонности функции будет в дальнейшем использоваться для решения нестандартных задач. Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. Д.Пойа Д.Пойа