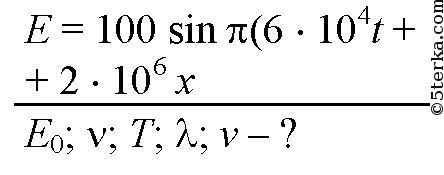Уравнение напряжения электрического поля бегущей электромагнитной

5. Уравнение напряженности электрического поля бегущей гармонической волны имеет вид Е = 100sin π (6 • 1014t+ 2 • 106x). Найдите: 1) амплитуду; 2) частоту; 3) период; 4) длину волны, 5) скорость и направление распространения волны. [1) 100 В.м; 2

Решебник по физике за 11 класс (Касьянов В.А., 2002 год),
задача №51
к главе «Излучение и прием электромагнитных волн радио- и СВЧ-диапазона. § 48. Распространение электромагнитных волн».

Выделите её мышкой и нажмите CTRL + ENTER

Большое спасибо всем, кто помогает делать сайт лучше! =)

Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.

Бегущие электромагнитные волны

Бегущие волны – это волны, которые переносят энергию в пространстве. Количественно транспортирование энергии этой волной назначает вектор плотности потока энергии, называемый вектором Умова-Пойтинга. Его направление совпадает с направлением распространения энергии. Модуль вектора равняется энергии, которую может переносить волна за время, равное 1 с , через площадку, располагаемую перпендикулярно к направлению ее движения с площадью, равняющуюся 1 .

Уравнение плоской бегущей волны

Для получения уравнения бегущей волны рассматривается плоская гармоническая. Считается, что она распространяется по О х . Поверхности волны перпендикулярны О х , все точки волновой поверхности совершают колебания одинаково, смещение ξ = ξ ( x , t ) будет функцией с координатой x и временем t . Запись уравнение колебаний частиц, находящихся на плоскости х , примет вид:

ξ ( x , t ) = A cos ω t — x υ ( 1 ) .

Отсюда ξ ( x , t ) является периодической по времени и по координате х . уравнение ( 1 ) называют уравнением бегущей волны. Если плоская волна задается при помощи выражения ( 1 ) , то ее перемещение идет по О х . При обратном ее направлении по О х уравнение запишется как:

ξ ( x , t ) = A cos ω t + x υ ( 2 ) .

Если волна движется по О х без поглощения энергии, то это характеризуется уравнением:

ξ ( x , t ) = A cos ω t — x υ + φ 0 ( 3 ) .

Значение A = c o n s t относят к амплитуде, ω – к циклической частоте волны, φ 0 — к начальной фазе колебаний, определяемой выбором началом отсчета x и t , ω t — x υ + φ 0 – к фазе плоской волны.

Что называют электромагнитной волной. Волновое число

Электромагнитные волны – это распространяющиеся в пространстве изменения состояния электромагнитного поля. Они характеризуются волновым числом k .

Запись выражения ( 1 ) примет совершенно другой вид при известном волновом числе.

Если перейти к комплексным числам, применив формулу Эйлера, уравнение плоской волны зафиксируем.

Выражение ( 6 ) имеет физический смысл только в действительной части, но R e возможно опустить в записи уравнения волны.

Перейдем к рассмотрению волнового процесса, где не происходит изменение фазы.

Далее найдем дифференциал от выражения ( 7 ) .

При условии, что υ волны зависит от частоты колебаний, то такая волна подвержена дисперсии.

Уравнение сферической бегущей волны

Сферическая волна – это волна, волновая поверхность которой является концентрической сферой. Такое уравнение примет вид:

ξ ( r , t ) = A 0 r cos ω t — k r + φ 0 ( 11 ) ,

где r является расстоянием от центра волны до точки рассмотрения. Если имеем дело со сферической волной, то ее амплитуда колебаний не будет постоянной даже при условии, что энергия не поглощается средой. Ее убывание происходит обратно пропорционально расстоянию. Выполнение уравнения ( 8 ) возможно тогда, когда источник волн считается точечным.

Уравнение бегущей волны в любом виде подчинено волновому уравнению.

Дана плоская электромагнитная волна в вакууме, которая распространяется по О х . Амплитуда напряженности электрического поля равняется E m . Определить амплитуду напряженности магнитного поля заданной волны.

За основу необходимо принять выражение для амплитуд электромагнитной волны:

ε ε 0 E = μ μ 0 H ( 1 . 1 ) .

Запись уравнения колебаний модуля E → в электромагнитной волне при условии, что она является плоской и идет по О х , фиксируем:

E = E m cos ω t — k x ( 1 . 2 ) .

Для записи уравнения колебаний H → в электромагнитной волне, в случае если она считается плоской и распространяется по О х :

H = H m cos ω t — k x ( 1 . 3 ) .

Из условия имеем, что волна производит рассеивание в вакууме, то ε = 1 , μ = 1 . Применяя ( 1 . 1 ) , ( 1 . 2 ) , ( 1 . 3 ) :

ε 0 E m = μ 0 H m → H m = ε 0 μ 0 E m .

Ответ: H m = ε 0 μ 0 E m .

Распространение электромагнитной плоской волны идет в вакууме по О х . Ее падение производится перпендикулярно поверхности тела, которое способно полностью поглощать волну. Значение амплитуды напряженности магнитного поля равняется
H m . Определить давление волны на тело.

Необходимо учитывать, что тело, которое поглощает падающую на него энергию, оказывается под давлением, равным среднему значению объемной плотности энергии в электромагнитной волне.

Следует применять соотношение амплитуд электромагнитной волны, которое записывается:

ε ε 0 E = μ μ 0 H .

Для того, чтобы зафиксировать уравнение колебаний E при распространении волны по О х , получим:

E = E m cos ω t — k x .

Теперь перейдем к уравнению колебаний H , если рассеивание плоской волны идет соответственно направлению О х . Запишем:

H = H m cos ω t — k x .

Следует, что значение объемной плотности электрической энергии примет вид:

ω E = ε ε 0 E 2 2 .

Формула плотности магнитного поля:

ω H = μ μ 0 H 2 2 .

Причем ω E = ω H . Запись примет вид:

ω = ω E + ω H = 2 ω H = μ μ 0 H 2 = μ μ 0 H m 2 cos 2 ω t — k x .

После усреднения плотности, имеем:

» open=» ω = » open=» μ μ 0 H m 2 cos 2 ω t — k x .

При » open=» cos 2 ω t — k x = 1 2 получаем:

p = » open=» ω = μ μ 0 H m 2 2 .

Ответ: p = » open=» ω = μ μ 0 H m 2 2 .

Бегущие электромагнитные волны

Вы будете перенаправлены на Автор24

Бегущими называют волны, переносящие энергию в пространстве. Количественно транспортирование энергии волной определяет вектор плотности потока энергии ( вектор Умова — Пойнтинга). Направление данного вектора такое же, как направление распространения энергии. Модуль данного вектора равен энергии, которую переносит волна за $1с$ через площадку, перпендикулярную к направлению движения волны, площадь которой — единица.

Уравнение плоской бегущей волны

Для того чтобы получить уравнение для бегущей волны, можно рассмотреть плоскую гармоническую волну. При этом будем считать, что данная волна распространяется по $оси X$. Тогда поверхности волны перпендикулярны $оси X$, и так как все точки волновой поверхности совершают колебания одинаково, то смещение ($\xi =\xi $(x,t)) будет функцией только координаты $(x)$ и $времени\ (t)$. Уравнение колебаний частиц, принадлежащих плоскости $x$, будут:

\[\xi \left(x,t\right)=Acos\omega \left(t-\frac\right)\left(1\right).\]

функция $\xi \left(x,t\right)$ — периодическая и по времени и по координате $x$. Уравнение (1) называется уравнением бегущей волны. Плоская волна, заданная уравнением (1) перемещается по $оси X$. В том случае, если плоская волна будет перемешаться против направления $оси X$, то ее уравнение запишется:

\[\xi \left(x,t\right)=Acos\omega \left(t+\frac\right)\left(2\right).\]

Волну, которая «бежит» по $оси X$, при этом не поглощает энергию, можно охарактеризовать уравнением:

\[\xi \left(x,t\right)=Acos\left[\omega \left(t-\frac\right)+<\varphi >_0\right]\left(3\right),\]

где $A=const$ — называется амплитудой, $\omega $ — носит название циклической частоты волны, $<\varphi >_0$- начальная фаза колебаний, которая определяется выбором начала отсчёта $x$ и $t.$ Выражение $\left[\omega \left(t-\frac\right)+<\varphi >_0\right]$ — называют фазой плоской волны.

Для того чтобы характеризовать волны, используют волновое число ($k$), равное:

Используя волновое число, уравнение (1) можно записать как:

Используя формулу Эйлера, перейдя к комплексным величинам, уравнение плоской волны запишется как:

В уравнении (6) физический смысл имеет только действительная часть, но значок $Re$ при записи уравнения волны часто опускают, имея это ввиду.

Рассмотрим волновой процесс, в котором фаза не изменятся:

Найдем дифференциал от выражения (7), имеем:

Из уравнения (8) следует, что:

Так, скорость ($v$) распространения волны — это скорость перемещения фазы волны. Такая скорость носит название фазовой скорости.

Из уравнения (4) следует, что:

Если $v$ волны зависима от частоты колебаний, то такая волна подвержена дисперсии.

Уравнение сферической бегущей волны

Сферической волной называют волны, волновые поверхности которых являются концентрическими сферами. Уравнение для подобной волны запишем как:

где $r$ — расстояние от центра волны то точки рассмотрения. Если мы имеем дело со сферической волной, то амплитуда колебаний не является постоянной, даже если энергия средой не поглощается. Она убывает обратно пропорционально расстоянию. Уравнение (8) выполняется только для случаев, когда источник волн можно считать точечным.