Как составить уравнение проекций ?

При решении задачек по статике, в теоретической механике или при решении задач по сопромату, часто, требуется определять сумму проекций сил на какую-то ось. Например, в термехе это используется при приведении какой-то системы сил к простейшему виду. В сопромате для определения реакций возникающих в опорах.

Уравнения проекций на примере

Рассмотрим, как составить уравнение проекций всех сил на какую-либо ось на примере. Возьмем прямоугольную декартову систему координат x-y и произвольную систему сил:

Проецируем все силы на координатные оси.Сила F1 дает положительную проекцию на ось X, так как ее направление совпадает с направлением этой оси. На ось Y эта сила не дает проекции, так как она перпендикулярная этой оси. Рассуждая, таким образом, можно записать следующие уравнения сумм проекций:

В выше описанном примере все силы были параллельны или перпендикулярны осям, но на практике же в задачах обычно силы расположены под некоторым углом к координатным осям. В таком случае силы раскладываются на две проекции параллельные осевым линиям:

Для нахождения этих сил удобнее вынести отдельно силовой треугольник и найти их следующим образом:

После этого можно записать уравнение проекций сил на горизонтальную и вертикальную ось:

Проекция точки на плоскость, координаты проекции точки на плоскость

В этой статье мы найдем ответы на вопросы о том, как создать проекцию точки на плоскость и как определить координаты этой проекции. Опираться в теоретической части будем на понятие проецирования. Дадим определения терминам, сопроводим информацию иллюстрациями. Закрепим полученные знания при решении примеров.

Проецирование, виды проецирования

Для удобства рассмотрения пространственных фигур используют чертежи с изображением этих фигур.

Проекция фигуры на плоскость – чертеж пространственной фигуры.

Очевидно, что для построения проекции существует ряд используемых правил.

Проецирование – процесс построения чертежа пространственной фигуры на плоскости с использованием правил построения.

Плоскость проекции — это плоскость, в которой строится изображение.

Использование тех или иных правил определяет тип проецирования: центральное или параллельное.

Частным случаем параллельного проецирования является перпендикулярное проецирование или ортогональное: в геометрии в основном используют именно его. По этой причине в речи само прилагательное «перпендикулярное» часто опускают: в геометрии говорят просто «проекция фигуры» и подразумевают под этим построение проекции методом перпендикулярного проецирования. В частных случаях, конечно, может быть оговорено иное.

Отметим тот факт, что проекция фигуры на плоскость по сути есть проекция всех точек этой фигуры. Поэтому, чтобы иметь возможность изучать пространственную фигуру на чертеже, необходимо получить базовый навык проецировать точку на плоскость. О чем и будем говорить ниже.

Проекция точки на плоскость

Напомним, что чаще всего в геометрии, говоря о проекции на плоскость, имеют в виду применение перпендикулярной проекции.

Произведем построения, которые дадут нам возможность получить определение проекции точки на плоскость.

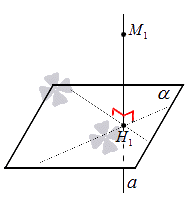
Допустим, задано трехмерное пространство, а в нем — плоскость α и точка М 1 , не принадлежащая плоскости α . Начертим через заданную точку М 1 прямую а перпендикулярно заданной плоскости α . Точку пересечения прямой a и плоскости α обозначим как H 1 , она по построению будет служить основанием перпендикуляра, опущенного из точки М 1 на плоскость α .

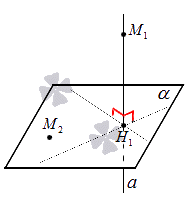
В случае, если задана точка М 2 , принадлежащая заданной плоскости α , то М 2 будет служить проекцией самой себя на плоскость α .

Проекция точки на плоскость – это либо сама точка (если она принадлежит заданной плоскости), либо основание перпендикуляра, опущенного из заданной точки на заданную плоскость.

Нахождение координат проекции точки на плоскость, примеры

Пускай в трехмерном пространстве заданы: прямоугольная система координат O x y z , плоскость α , точка М 1 ( x 1 , y 1 , z 1 ) . Необходимо найти координаты проекции точки М 1 на заданную плоскость.

Решение очевидным образом следует из данного выше определения проекции точки на плоскость.

Обозначим проекцию точки М 1 на плоскость α как Н 1 . Согласно определению, H 1 является точкой пересечения данной плоскости α и прямой a , проведенной через точку М 1 (перпендикулярной плоскости). Т.е. необходимые нам координаты проекции точки М 1 – это координаты точки пересечения прямой a и плоскости α .

Таким образом, для нахождения координат проекции точки на плоскость необходимо:

— получить уравнение плоскости α (в случае, если оно не задано). Здесь вам поможет статья о видах уравнений плоскости;

— определить уравнение прямой a , проходящей через точку М 1 и перпендикулярной плоскости α (изучите тему об уравнении прямой, проходящей через заданную точку перпендикулярно к заданной плоскости);

— найти координаты точки пересечения прямой a и плоскости α (статья – нахождение координат точки пересечения плоскости и прямой). Полученные данные и будут являться нужными нам координатами проекции точки М 1 на плоскость α .

Рассмотрим теорию на практических примерах.

Определите координаты проекции точки М 1 ( — 2 , 4 , 4 ) на плоскость 2 х – 3 y + z — 2 = 0 .

Решение

Как мы видим, уравнение плоскости нам задано, т.е. составлять его необходимости нет.

Запишем канонические уравнения прямой a , проходящей через точку М 1 и перпендикулярной заданной плоскости. В этих целях определим координаты направляющего вектора прямой a . Поскольку прямая а перпендикулярна заданной плоскости, то направляющий вектор прямой a – это нормальный вектор плоскости 2 х – 3 y + z — 2 = 0 . Таким образом, a → = ( 2 , — 3 , 1 ) – направляющий вектор прямой a .

Теперь составим канонические уравнения прямой в пространстве, проходящей через точку М 1 ( — 2 , 4 , 4 ) и имеющей направляющий вектор a → = ( 2 , — 3 , 1 ) :

x + 2 2 = y — 4 — 3 = z — 4 1

Для нахождения искомых координат следующим шагом определим координаты точки пересечения прямой x + 2 2 = y — 4 — 3 = z — 4 1 и плоскости 2 х — 3 y + z — 2 = 0 . В этих целях переходим от канонических уравнений к уравнениям двух пересекающихся плоскостей:

x + 2 2 = y — 4 — 3 = z — 4 1 ⇔ — 3 · ( x + 2 ) = 2 · ( y — 4 ) 1 · ( x + 2 ) = 2 · ( z — 4 ) 1 · ( y — 4 ) = — 3 · ( z + 4 ) ⇔ 3 x + 2 y — 2 = 0 x — 2 z + 10 = 0

Составим систему уравнений:

3 x + 2 y — 2 = 0 x — 2 z + 10 = 0 2 x — 3 y + z — 2 = 0 ⇔ 3 x + 2 y = 2 x — 2 z = — 10 2 x — 3 y + z = 2

И решим ее, используя метод Крамера:

∆ = 3 2 0 1 0 — 2 2 — 3 1 = — 28 ∆ x = 2 2 0 — 10 0 — 2 2 — 3 1 = 0 ⇒ x = ∆ x ∆ = 0 — 28 = 0 ∆ y = 3 2 0 1 — 10 — 2 2 2 1 = — 28 ⇒ y = ∆ y ∆ = — 28 — 28 = 1 ∆ z = 3 2 2 1 0 — 10 2 — 3 2 = — 140 ⇒ z = ∆ z ∆ = — 140 — 28 = 5

Таким образом, искомые координаты заданной точки М 1 на заданную плоскость α будут: ( 0 , 1 , 5 ) .

Ответ: ( 0 , 1 , 5 ) .

В прямоугольной системе координат O x y z трехмерного пространства даны точки А ( 0 , 0 , 2 ) ; В ( 2 , — 1 , 0 ) ; С ( 4 , 1 , 1 ) и М₁(-1, -2, 5). Необходимо найти координаты проекции М 1 на плоскость А В С

Решение

В первую очередь запишем уравнение плоскости, проходящей через три заданные точки:

x — 0 y — 0 z — 0 2 — 0 — 1 — 0 0 — 2 4 — 0 1 — 0 1 — 2 = 0 ⇔ x y z — 2 2 — 1 — 2 4 1 — 1 = 0 ⇔ ⇔ 3 x — 6 y + 6 z — 12 = 0 ⇔ x — 2 y + 2 z — 4 = 0

Далее рассмотрим еще один вариант решения, отличный от того, что мы использовали в первом примере.

Запишем параметрические уравнения прямой a , которая будет проходить через точку М 1 перпендикулярно плоскости А В С . Плоскость х – 2 y + 2 z – 4 = 0 имеет нормальный вектор с координатами ( 1 , — 2 , 2 ) , т.е. вектор a → = ( 1 , — 2 , 2 ) – направляющий вектор прямой a .

Теперь, имея координаты точки прямой М 1 и координаты направляющего вектора этой прямой, запишем параметрические уравнения прямой в пространстве:

x = — 1 + λ y = — 2 — 2 · λ z = 5 + 2 · λ

Затем определим координаты точки пересечения плоскости х – 2 y + 2 z – 4 = 0 и прямой

x = — 1 + λ y = — 2 — 2 · λ z = 5 + 2 · λ

Для этого в уравнение плоскости подставим:

x = — 1 + λ , y = — 2 — 2 · λ , z = 5 + 2 · λ

Теперь по параметрическим уравнениям x = — 1 + λ y = — 2 — 2 · λ z = 5 + 2 · λ найдем значения переменных x , y и z при λ = — 1 : x = — 1 + ( — 1 ) y = — 2 — 2 · ( — 1 ) z = 5 + 2 · ( — 1 ) ⇔ x = — 2 y = 0 z = 3

Таким образом, проекция точки М 1 на плоскость А В С будет иметь координаты ( — 2 , 0 , 3 ) .

Ответ: ( — 2 , 0 , 3 ) .

Отдельно остановимся на вопросе нахождения координат проекции точки на координатные плоскости и плоскости, которые параллельны координатным плоскостям.

Пусть задана точки М 1 ( x 1 , y 1 , z 1 ) и координатные плоскости O x y , О x z и O y z . Координатами проекции этой точки на данные плоскости будут соответственно: ( x 1 , y 1 , 0 ) , ( x 1 , 0 , z 1 ) и ( 0 , y 1 , z 1 ) . Рассмотрим также плоскости, параллельные заданным координатным плоскостям:

C z + D = 0 ⇔ z = — D C , B y + D = 0 ⇔ y = — D B

И проекциями заданной точки М 1 на эти плоскости будут точки с координатами x 1 , y 1 , — D C , x 1 , — D B , z 1 и — D A , y 1 , z 1 .

Продемонстрируем, как был получен этот результат.

В качестве примера определим проекцию точки М 1 ( x 1 , y 1 , z 1 ) на плоскость A x + D = 0 . Остальные случаи – по аналогии.

Заданная плоскость параллельна координатной плоскости O y z и i → = ( 1 , 0 , 0 ) является ее нормальным вектором. Этот же вектор служит направляющим вектором прямой, перпендикулярной к плоскости O y z . Тогда параметрические уравнения прямой, проведенной через точку M 1 и перпендикулярной заданной плоскости, будут иметь вид:

x = x 1 + λ y = y 1 z = z 1

Найдем координаты точки пересечения этой прямой и заданной плоскости. Подставим сначала в уравнение А x + D = 0 равенства: x = x 1 + λ , y = y 1 , z = z 1 и получим: A · ( x 1 + λ ) + D = 0 ⇒ λ = — D A — x 1

Затем вычислим искомые координаты, используя параметрические уравнения прямой при λ = — D A — x 1 :

x = x 1 + — D A — x 1 y = y 1 z = z 1 ⇔ x = — D A y = y 1 z = z 1

Т.е., проекцией точки М 1 ( x 1 , y 1 , z 1 ) на плоскость будет являться точка с координатами — D A , y 1 , z 1 .

Необходимо определить координаты проекции точки М 1 ( — 6 , 0 , 1 2 ) на координатную плоскость O x y и на плоскость 2 y — 3 = 0 .

Решение

Координатной плоскости O x y будет соответствовать неполное общее уравнение плоскости z = 0 . Проекция точки М 1 на плоскость z = 0 будет иметь координаты ( — 6 , 0 , 0 ) .

Уравнение плоскости 2 y — 3 = 0 возможно записать как y = 3 2 2 . Теперь просто записать координаты проекции точки M 1 ( — 6 , 0 , 1 2 ) на плоскость y = 3 2 2 :

Ответ: ( — 6 , 0 , 0 ) и — 6 , 3 2 2 , 1 2

Определение свойств картографических проекций по их уравнениям

Описание: Цель работы: усвоение положений общей теории картографических проекций которые являются основополагающими при изучении раздела Математическая картография Исходные данные: Картографическая проекция задана уравнениями: По заданным уравнениям картографической проекции определить: — ортогональность картографической сетки; — частные масштабы длин m n b масштаб площадей р максимальное искажение углов ω; — группу проекций по характеру искажений к которой относится заданная проекция — вид картографической сетки. Функции.

Дата добавления: 2015-10-26

Размер файла: 41.99 KB

Работу скачали: 19 чел.

Поделитесь работой в социальных сетях

Если эта работа Вам не подошла внизу страницы есть список похожих работ. Так же Вы можете воспользоваться кнопкой поиск

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА И ПРОДОВОЛЬСТВИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

БЕЛОРУССКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ

Кафедра геодезии и фотограмметрии

Лабораторная работа № 1

Определение свойств картографических проекций по их уравнениям

Выполнила: ст. 4к. 2 гр.

Проверила: Ларионова Е. В.

Цель работы : усвоение положений общей теории картографических проекций, которые являются основополагающими при изучении раздела «Математическая картография»

Исходные данные: Картографическая проекция задана уравнениями:

По заданным уравнениям картографической проекции определить:

— ортогональность картографической сетки;

— частные масштабы длин m , n , a , b , масштаб площадей р, максимальное искажение углов ω;

— группу проекций по характеру искажений, к которой относится заданная проекция,

— вид картографической сетки.

Математическая зависимость между координатами точек земной поверхности и плоскими прямоугольными координатами этой точки на плоскости может быть выражена следующей формулами:

Где х, у – плоские прямоугольные координаты на кате;

— географические координаты этой точки на шаре или эллипсоиде.

Функции f 1 , f 2 – конечные, непрерывные для изображаемой области, свойства проекции зависят от вида этих функций.

Последовательность выполнения задания рассмотрим на конкретном примере.

Пример. Картографическая проекция задана уравнениями:

Сначала определим частные производные

Найдем коэффициенты Гауса:

1. Определение ортогональной плоскости картографической сетки

Сетка проекции является ортогональной, так как коэффициент Гаусса f =0.

1. Вычисление частных масштабов длин m , n , a , b , масштаба площади р, максимального искажения ω

Частный масштаб длин вдоль меридианов определяется выражением

Выражение частного масштаба длин параллелей имеет вид:

Поскольку сетка проекции ортогональна, то главные направления совпадают с меридианами и параллелями а экстремальные масштабы длин a и b совпадают с масштабами длин m и n . В данном случае: если m > n , то a = m и b = n

Если m n , то a = n , т.е. , то а= n =, и b = m =

Частный масштаб площадей рассчитывается по формуле:

Максимальное искажение углов ω находим по одной из формул:

1. Определение группы проекций по характеру искажений

Все проекции по характеру искажений делятся на три группы равноугольные, равновеликие и произвольные. Т.к. выполняется условие: f =0, m ≠ n , то картографическая проекция не является равноугольной.

Т.к. p ≠ cons ’ t , то картографическая проекция является не является равновеликой.

Из этого следует, что проекция произвольная, где присутствуют искажения в разных видах.

1. Определение вида картографической сетки.

Из общей теории картографических проекций известно, что

F 1 ( x , y , φ )=0 — уравнение параллелей;

F 2 ( x , y , λ )=0 — уравнение меридианов, поэтому для получения уравнения параллелей из данных уравнений проекции необходимо исключить долготу λ , а для получения уравнения меридианов — широту φ .

В нашем случае уравнение x = R φsin λ является уравнением параллелей, поскольку х является функцией одного аргумента — широты.

Последнее уравнение является уравнением меридиана и в то же время уравнением синусоиды. Для построения эскиза сетки необходимо определить вид географического полюса в проекции.

Географический полюс Р в проекции может изображаться:

— в виде прямой линии

— в виде кривой линии

В данном случае полюс в проекции не будет изображаться вовсе.

Вывод: По заданным уравнениям картографической проекции мною было определено следующее: сетка ортогональна (коэффициент Гауса равен 0), масштабы длин m и b совпадают с масштабами длин m и n , картографическая проекция произвольна, где присутствуют искажения в разных видах.