Уравнение непрерывности для электрического заряда
1.7.2. Уравнение непрерывности
Если внутри проводника, по которому течет электрический ток, выделить какой-то объем, ограниченный замкнутой поверхностью S (рис 1.7.2), то, согласно закону сохранения электрического заряда, суммарный электрический заряд q, охватываемый поверхностью S, изменяется за время dt на dq = —Idt, тогда в интегральной форме можно записать:
Это соотношение называется уравнением непрерывности. Оно является, по существу, выражением закона сохранения электрического заряда.
Дифференциальная форма записи уравнения непрерывности записывается так:
В случае постоянного тока распределение зарядов в пространстве должно оставаться неизменным:
— это уравнение непрерывности для постоянного тока (в интегральной форме).
Линии j в этом случае нигде не начинаются и нигде не заканчиваются. Поле вектора j не имеет источника. В дифференциальной форме уравнение непрерывности для постоянного тока .
Уравнение непрерывности для электрического заряда
Напомним, что все электрические заряды, встречающиеся в природе, являются по абсолютному значению кратными элементарному заряду, равному заряду электрона, причем этот элементарный заряд является постоянным и не зависит от скорости частицы, которая несет этот заряд. Простейшим доказательством независимости величины заряда от его скорости является факт электронейтральности атомов, в которых заряд быстродвижущихся электронов полностью компенсирует заряд ядра. Заряд любого тела также является величиной, инвариантной относительно переходов из одной инерциальной системы в другую, и это утверждение составляет один аспект закона сохранения зарядов.
С другой стороны, как показывает вся совокупность опытных фактов, ни каких физических процессах суммарное количество зарядов не изменяется . Отсюда, конечно, не следует, что сохраняются в отдельности положительные и отрицательные заряды системы; например, в процессе аннигиляции электрон — позитронной пары число положительных и отрицательных зарядов уменьшается, но при этом суммарное количество зарядов остается неизменным. Постоянство суммарного заряда в физическом процессе представляет собой вторую сторону закона сохранения заряда.
Таким образом, из закона сохранения заряда следует, что полный заряд системы может изменяться только за счет пересечения ее границы заряженными частицами. Это утверждение математически может быть представлено в виде соотношения между макроскопическими величинами ρ (плотность заряда) и j → (плотность тока), характеризующими процесс протекания тока. Для этого в пространстве, занятом током, мысленно выделим некоторый объем V , ограниченный замкнутой поверхностью S . Суммарное количество заряда, ежесекундно уходящее из объема V через поверхность S , определяется интегралом (3.3). Обусловленная этим скорость изменения суммарного заряда в объеме V равна
− ∂ ∂ t ∫ ρ d V = ∫ ( − ∂ ρ ∂ t ) d V .
Приравнивая эти две величины, получаем соотношение
| ∂ ∂ t ∫ ρ d V = − ∮ S j n d S , | (21.1) |
являющееся интегральным представлением закона сохранения заряда . Выражая входящий сюда поверхностный интеграл с помощью теоремы Остроградского — Гаусса, результат можно переписать в виде ∫ V ( ∂ ρ ∂ t + d i v j → ) d V = 0 .
Поскольку это равенство должно выполняться для произвольного объема V , подинтегральное выражение тождественно должно равняться нулю, т. е.
| ∂ ρ ∂ t + d i v j → = 0 . | (21.2) |
Полученное уравнение называется уравнением непрерывности . Это есть дифференциальное представление закона сохранения заряда .
Если рассматривается стационарный процесс, при котором токи и заряды не меняются со временем, уравнения (3.6), (3.7) принимают вид
Уравнение непрерывности и закон сохранения зарядов
Из первого и третьего уравнений Максвелла вытекает важное соотношение, называемое уравнением непрерывности:
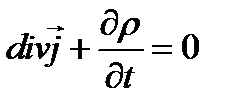
Правая часть уравнения (1.28) представляет собой сумму плотностей тока проводимости и тока смещения, т.е. плотность полного тока 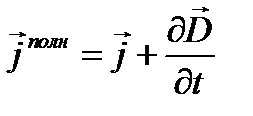
Уравнение (1.21) можно переписать
Уравнение (1.22) представляет собой закон сохранения заряда: всякому изменению величины заряда, распределенного в некоторой области, соответствует электрический ток I, втекающий в эту область или вытекающий из нее.
Граничные условия
Рассматриваемая на практике область может состоять из двух (и более) разнородных сред. На границе раздела сред параметры e, m и s меняются скачком. Соотношения, показывающие связь между значениями составляющих векторов электромагнитного поля в разных средах у поверхности раздела, называют граничными условиями. Данные соотношения получены по отдельности для нормальных (перпендикулярных) и тангенциальных (касательных) проекций электрических и магнитных векторов.
Граничное условие для нормальной составляющей вектора D в общем случае имеет вид:
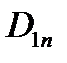
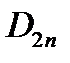
Здесь τ – поверхностная плотность заряда – характеризует заряд, распределенный вдоль поверхности раздела.
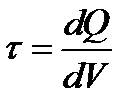
В случае если заряд не сосредоточен на поверхности раздела, т.е. не является поверхностным, то правая часть формулы (1.24) равна нулю, а нормальная компонента вектора D непрерывна при переходе из одной среды в другую:
Выражение (1.25) показывает, что при отсутствии на границе раздела двух сред поверхностных зарядов нормальная составляющая вектора электрического смещения меняется плавно, при наличии поверхностных зарядов – меняется скачкообразно.
Воспользовавшись материальным уравнением (1.4) можно получить граничное условие для напряженности электрического поля
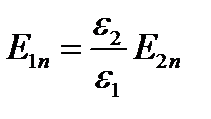
Выражение (1.26) показывает, что нормальная составляющая вектора напряженности электрического поля меняется скачком.
Граничное условие для нормальной составляющей вектора магнитной индукции имеет вид
Выражая в равенстве (1.27) Bn через Нn, получаем
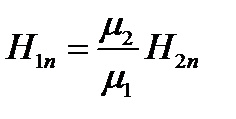
Граничное условие для касательных составляющих вектор напряженности магнитного поля имеет вид:
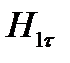
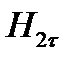
jsl – плотность поверхностного тока. Она определяется соотношением:
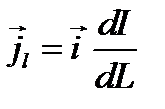
Выражение (1.30) характеризует токи, распределенные вдоль поверхности раздела в виде бесконечно тонкого слоя. Такие токи называют поверхностными.
В случае отсутствия поверхностных токов можем записать:
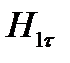
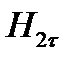
Выражение (1.31) показывает, что при отсутствии на границе раздела двух сред поверхностных токов касательная составляющая вектора напряженности магнитного поля меняется плавно, при наличии поверхностных токов – меняется скачкообразно.
Касательная составляющая вектора В, наоборот, претерпевает разрыв, величина которого определяется отношением магнитных проницаемостей:
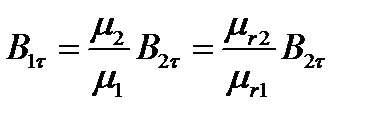
Граничное условие для касательной составляющей вектора Е:
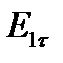
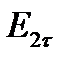
Касательная составляющая вектора Dпретерпевает разрыв, величина которого зависит от соотношения между диэлектрическими проницаемостями:
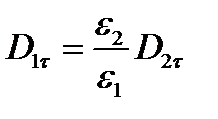
http://phys.nsu.ru/cherk/eldinfirst/wese21.html
http://helpiks.org/5-101597.html