Уравнение непрерывности для постоянного тока

Измерительные приборы, определяющие ток.

Приборы нагревательных элементов.

Происходят химические превращения при протекании тока.

5.Уравнение непрерывности

Закон сохранения заряда утверждает, что в замкнутой системе заряд сохраняется. Если система не замкнута, то заряд может изменяться.

Данное уравнение называется уравнением непрерывности в интегральной форме. Производная по времени связана с временной зависимостью заряда. Данное уравнение считается постулатом. По смыслу – это закон изменения заряда.

Используя понятие объемной плотности заряда и формулу Остроградского-Гаусса

– уравнение непрерывности в дифференциальной форме.

Если ток постоянный, то , следовательно, линии плотности тока являются замкнутыми.

6.Поле в проводнике при постоянном токе

Если есть ток, значит, есть движение зарядов, следовательно, есть сила, которая заставляет двигаться заряды, есть ток, есть напряженность, которая направлена вдоль тока. В общем случае напряженность направлена под углом к поверхности. Если есть напряженность, то градиент потенциала вдоль проводника не равен нулю, следовательно, потенциал вдоль проводника изменяется. Говорят о падении потенциала.

7.Закон Ома в дифференциальной форме

Плотность тока и напряженность вдоль проводника взаимосвязаны между собой. Разумно предположить, что это самая простая связь, т.е. линейная.

где σ – удельная электропроводность.

Данный закон является постулатом.

Для металлов закон выполняется почти всегда, для полуметаллов начинаются отклонения при очень больших плотностях тока. Для других линейную связь можно заменить тензорной и закон Ома замыкает уравнения Максвелла.

Из этого соотношения следует, что линии плотности тока и линии напряженности при постоянном токе совпадают, а, следовательно, распределение полей можно изучать по распределению тока (метод электролитической ванны).

8.Закон Ома в интегральной форме.

Наряду с удельной электропроводностью, вводят понятие удельного сопротивления.

Сила тока I вдоль проводника не изменяется.

Интеграл в левой части назовем сопротивлением проводника между точками 1 и 2.

– напряжение между точками электрической цепи.

– закон Ома в интегральной форме.

9.Сопротивление и проводимость.

Сопротивление зависит от геометрии и от вещества, из которого сделан проводник.

Для цилиндрического проводника одинакового поперечного сечения оно вычисляется особенно просто.

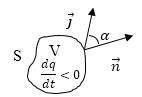
Измерив сопротивление, можно вычислить ёмкость и наоборот.

Данное устройство иногда называется конденсатором с утечкой.

По физическому смыслу, удельное сопротивление – это сопротивление куба вещества с ребром 1 м, если подводящие провода подключены к центрам противоположных граней.

Уравнение непрерывности для постоянного тока

1.7.2. Уравнение непрерывности

Если внутри проводника, по которому течет электрический ток, выделить какой-то объем, ограниченный замкнутой поверхностью S (рис 1.7.2), то, согласно закону сохранения электрического заряда, суммарный электрический заряд q, охватываемый поверхностью S, изменяется за время dt на dq = —Idt, тогда в интегральной форме можно записать:

Это соотношение называется уравнением непрерывности. Оно является, по существу, выражением закона сохранения электрического заряда.

Дифференциальная форма записи уравнения непрерывности записывается так:

В случае постоянного тока распределение зарядов в пространстве должно оставаться неизменным:

— это уравнение непрерывности для постоянного тока (в интегральной форме).

Линии j в этом случае нигде не начинаются и нигде не заканчиваются. Поле вектора j не имеет источника. В дифференциальной форме уравнение непрерывности для постоянного тока .

Уравнение непрерывности

Вы будете перенаправлены на Автор24

Допустим, что в некоторой среде течет ток, выделим в этой среде гипотетическую замкнутую поверхность S (рис.1).

Исходя из закона сохранения заряда, как эмпирического факта, определим, что заряд, выходящий из объема V, который ограничен поверхностью S в единицу времени ($\frac<\partial q><\partial t>$), будет равен:

Знак минус учитывает, что если положительный заряд внутри объема уменьшается, то плотность тока направлена из объема V. Напомним, что у замкнутых объёмов положительной нормалью считается внешняя нормаль. Получается, что вектор $d\overrightarrow$ направлен по внешней нормали.

Представим элементарный заряд в виде:

Из выражения (1) получим:

Под знаком интеграла в правой части стоит частная производная, так как плотность заряда может зависеть не только от времени, но и координат. В левой части (3) перейдем от поверхностного интеграла к объемному, получим:

В таком случае выражение (3) можно представить как:

Уравнение (5) должно выполняться для любого объема, следовательно:

Выражение (6) носит название — уравнение непрерывности (уравнение неразрывности). Оно входит в систему уравнений Максвелла в неявном виде. Уравнение непрерывности выражает закон сохранения заряда. Согласно уравнению (6) в точках, которые являются источниками вектора плотности тока ($\overrightarrow$), происходит убывание заряда.

Уравнение неразрывности для стационарных токов

В том случае, если токи не зависят от времени, то уравнение (1) переходит в следующее выражение:

А уравнение (6) в равенство:

Уравнение (8) показывает, что если ток является постоянным, то $\overrightarrow$ не имеет источников. Это значит, что лини тока нигде не начинаются и нигде не заканчиваются. Можно сделать вывод о том, что линии постоянного тока всегда замкнуты. Под линиями токов в данном случае следует понимать лини вектора $\overrightarrow.$ (касательные к которым совпадают с направлением вектора плотности тока в точке касания). Что напрямую следует из (7).

Готовые работы на аналогичную тему

Благодаря замкнутости постоянных токов их можно разложить на совокупность бесконечных замкнутых тонких нитей тока.

Задание: Из уравнения$\ rot\overrightarrow=\frac<4\pi >\overrightarrow+\frac<1>\frac<\partial \overrightarrow><\partial t>$, которое принадлежит системе уравнений Максвелла (СГС), получите уравнения непрерывности токов и закон сохранения заряда.

где $\overrightarrow$ — напряженность магнитного поля, $c-\ $скорость света в вакууме,$\ \overrightarrow$ — вектор электрического смещения.

Проведем для него операцию дивергенции ($div\ или\ \nabla $). Получим:

\[\nabla \left(rot\ \overrightarrow\right)=0\left(1.2\right).\] \[\ \nabla \left(\frac<4\pi >\overrightarrow+\frac<1>\frac<\partial \overrightarrow><\partial t>\right)=\frac<1><с>\left(4\pi \nabla \overrightarrow+\frac<\partial ><\partial t>\nabla \overrightarrow\right)(1.3).\]

\[\nabla \overrightarrow=4\pi \rho \left(1.4\right).\]

Подставим (1.4) в (1.3) получим:

\[\frac<1><с>\left(4\pi \nabla \overrightarrow+\frac<\partial ><\partial t>4\pi \rho \right)=0\left(1.5\right).\]

от сюда следует:

или в интегральной форме:

Соответственно для замкнутых изолированных областей получим:

\[\oint\nolimits_S=0\ (1.8)\] \[\int\nolimits_V<\rho dV>=const\ (1.9)\]

Это уравнение непрерывности для тока, содержащее в себе закон сохранения заряда — один из фундаментальных принципов, который подтверждается экспериментом.

Задание: Объясните, как ведет себя нормальная составляющая вектора плотности тока при переходе через границу двух проводящих сред, для стационарных токов. Что можно сказать относительно нормальной составляющей плотности тока для проводника, который находится в непроводящей среде?

На поверхности соприкосновения двух проводников может испытывать разрыв непрерывности. Но, его нормальная составляющая ($j_n$) должна быть одинаковой по обе стороны границы сред. В противном случае количество электричества, которое притекает к одной стороне не равно, количеству электричества, которое вытекает с другой стороны. Значит:

где $j_<1n>-$нормальная составляющая плотность тока в среде (1), $j_<2n>-$нормальная составляющая плотность тока в среде (2).

В непроводящей среде $\overrightarrow=0$. Следовательно, нормальная составляющая к поверхности проводника плотности тока также должна быть равна нулю: