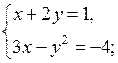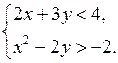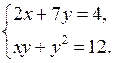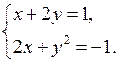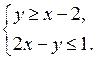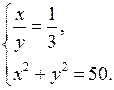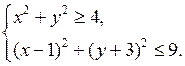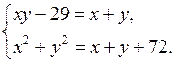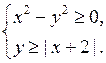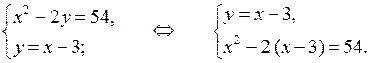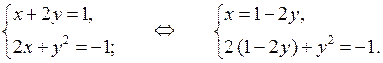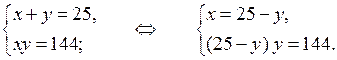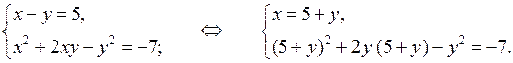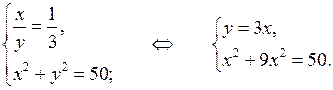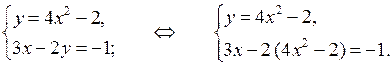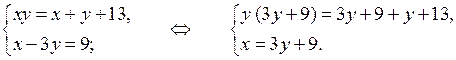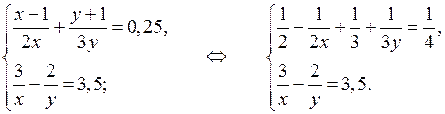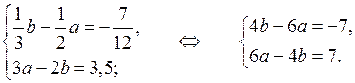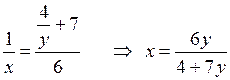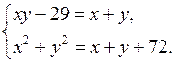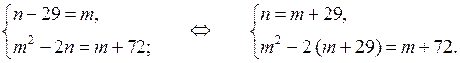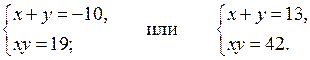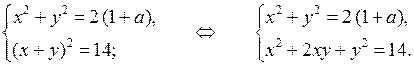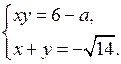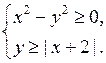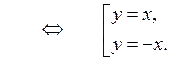Урок в 9 классе «Уравнения и неравенства с двумя переменными»
У р о к
Итоговый урок по теме «Уравнения
и неравенства с двумя переменными»
Цели: обобщить и систематизировать знания учащихся по данной теме; закрепить умения решать уравнения, неравенства и их системы с двумя переменными.
I. Организационный момент.
II. Устная работа.
Какие из пар чисел (0; 3), (1; –2), (–1; 1) являются решениями данных систем?
а) 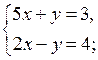
б) 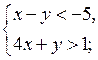
III. Формирование умений и навыков.
Предложить учащимся карточки-задания разного уровня сложности. Учащиеся выполняют решения самостоятельно, а учитель осуществляет контроль и в случае необходимости дает им консультации.
К а р т о ч к а № 1
1. Докажите, что пара чисел (–5; 2) не является решением системы уравнений
2. Решите систему уравнений:
а) 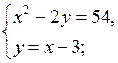
3. Сумма двух чисел равна 25, а их произведение равно 144. Найдите эти числа.
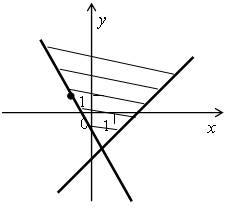
4. Изобразите на координатной плоскости множество решений системы неравенств:
а) 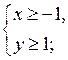
К а р т о ч к а № 2
1. Решите систему уравнений:
а) 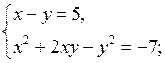
2. Не выполняя построения, найдите координаты точек пересечения параболы у = 4х 2 – 2 и прямой 3х – 2у = –1.
3. Произведение двух чисел на 13 больше их суммы. Если из первого числа вычесть утроенное второе число, то получится 9. Найдите эти числа.
4. Изобразите на координатной плоскости множество решений системы неравенств:
а) 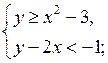
К а р т о ч к а № 3*
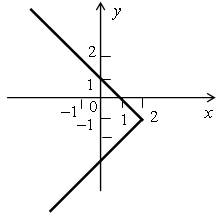
1. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют уравнению | у + 1 | = 2 – х.
2. Решите систему уравнений:
а) 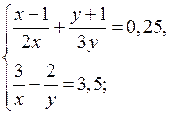
3. При смешивании первого раствора кислоты, концентрация которого 20 %, и второго раствора этой же кислоты, концентрация которого 50 %, получили раствор, содержащий 30 % кислоты. В каком отношении были взяты первый и второй растворы?
4. При каких значения параметра а система уравнений:
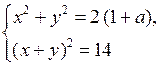
5. Изобразите на координатной плоскости множество решений системы неравенств:
Р е ш е н и е заданий карточки № 1
1. Подставим х = –5 и у = 2 в каждое из уравнений системы:
Значит, пара чисел (–5; 2) не является решением данной системы.
а)
х 1 = –6 
х 2 = 8 
О т в е т: (–6; –9), (8; 5).
б)
у 1 = 1 
у 2 = 3 
О т в е т: (–1; 1), (–5; 3).
3. Обозначим первое число за х, а второе – за у. Согласно условию задачи получим систему уравнений:
D = 625 – 4 · 144 = 49;
у 1 = 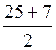

у 2 = 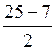

О т в е т: 9 и 16.
а) 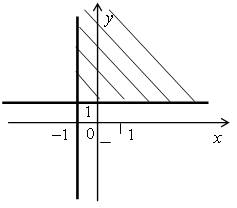
Р е ш е н и е заданий карточки № 2
1. а)
у 1 = –2 
у 2 = –8 
О т в е т: (3; –2), (–3; –8).
б)
х 1 = 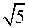

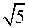
х 2 = – 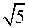

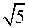
О т в е т: (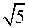
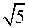
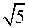
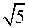
2. Чтобы найти координаты точек пересечения данных параболы и прямой, нужно решить систему уравнений:
х 1 = 1 
х 2 = 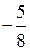

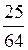
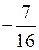
О т в е т: (1; 2), 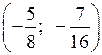
3. Обозначим первое число за х, а второе – за у. Согласно условию задачи получим систему уравнений:
D = 25 + 264 = 289;
у 1 = 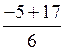

у 2 = 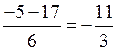

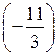
О т в е т: (15; 2), 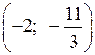
а) 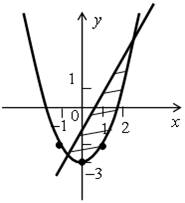
Р е ш е н и е заданий карточки № 3*
1. Раскрывая модуль, получим совокупность двух уравнений:
1) если у ≥ –1, то у + 1 = 2 – х,
Изобразим на координатной плоскости оба этих случая:
а)
Сделаем замену: 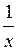
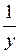
Складывая почленно левые и правые части уравнений этой системы, получим равенство:
Значит, система имеет бесконечное множество решений.
Выразим из второго уравнения переменную а через переменную b:
a = 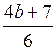
Возвращаясь к замене, получим:
Получаем, что исходная система имеет бесконечное множество решений вида 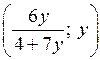
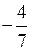
Например, это могут быть такие пары, как 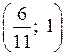
б)
Обозначим х + у = т, а ху = п. Тогда имеем:
т 1 = –10 
т 2 = 13 
Возвращаясь к замене, получим системы:
Решая эти системы, получаем ответ.
О т в е т: (6; 7), (7; 6), (–5 + 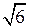
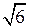
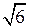
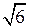
3. Пусть было взято x г первого раствора и y г – второго раствора. По условию в первом растворе было 0,2x г кислоты, а во втором – 0,5y г кислоты.
После смешивания получили 30 %-ный раствор, то есть в нем было 0,3 (x + y) г кислоты. Масса кислоты после смешивания двух растворов равна сумме масс исходных растворов.
Получаем, что первый и второй растворы были взяты в отношении 2 : 1.
4.
Вычтем почленно из второго уравнения системы первое:
Тогда данную систему уравнений можно представить как совокупность двух систем:
1) 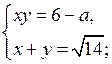
Исходная система будет иметь два решения в трех случаях:
– если каждая из систем имеет по одному решению;
– если первая система имеет два решения, а вторая – решений не имеет;
– если вторая система имеет два решения, а первая – решений не имеет.
Если в каждой из полученных систем выразить одну переменную через другую и найти дискриминант, то в обоих случаях получим:
Выражение 4а – 10 не может быть одновременно больше и меньше нуля, поэтому подходит тот случай, когда каждая из систем имеет единственное решение, то есть, когда D = 0:
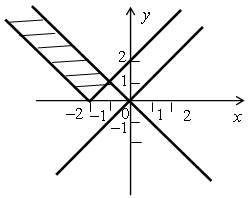
5.
Для построения графика уравнения х 2 – у 2 = 0 воспользуемся формулой разности квадратов. Получим:
(х – у) (х + у) = 0
Для построения графика уравнения у = | х + 2 | необходимо раскрыть знак модуля и рассмотреть два случая.
Домашнее задание: № 527 (а, г), № 528 (а), № 529 (а), № 542, № 555.
Конспекты 4 уроков по алгебре в 9 классах по теме «Решение систем неравенств с 2 переменными.Контрольная работа по теме :Системы уравнений и неравенств с 2 переменным ( с решением)»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Алгебра 9 класс Урок №___________________________________________________
Решение систем неравенств второй степени с двумя переменными
Тип урока: Урок формирования новых знаний.
Развивать вычислительные навыки при решении систем уравнений второй степени
Сформировать понятие системы неравенств
формировать умение решать системы неравенств второй степени с двумя переменными.
Рассмотреть два способа решения систем неравенств (графический и аналитический способы) и научиться их решать, пользуясь алгоритмом
проконтролировать степень усвоения материала по теме.
способствовать развитию навыка самостоятельного применения знаний;
развивать навыки самоконтроля;
продолжить работу по развитию логического мышления и устной математической речи при поиске решения поставленной проблемы.
приучать к умению общаться и выслушивать других;
воспитывать внимательность и наблюдательность;
стимулировать мотивацию и интерес к изучению математики.
Цель деятельности учителя
Создать условия для формирования способов решения систем решении задач
Термины и понятия
Системы неравенств, способы решения
Универсальные учебные действия
У меют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности
Познавательные: осуществляют логические действия; формулируют ответы на вопросы.
Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения математических проблем, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения.
Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.
Личностные: проявляют способность к эмоциональному восприятию математатических объектов, задач, решений, рассуждений
Фронтальная (Ф); индивидуальная (И)
I. Организационный момент.
II. Устная работа. Является ли решением системы неравенств 
III .Проверка домашней работы (решение примеров ,аналогичных ДР)
IV. Объяснение нового материала. Сначала необходимо актуализировать знания учащихся о решении систем линейных неравенств с двумя переменными, а затем разобрать пример 2 из учебника.
Формирование умений и навыков. Упражнения:
1. Изобразите на координатной плоскости множество решений системы:
а) 
Изобразим на координатной плоскости множество решений этой системы, предварительно преобразовав ее:
Таким образом, множество решений этой системы неравенств задает треугольник ОАВ . Для нахождения его площади нужно знать высоту ВН , то есть абсциссу точки В . Точка В является точкой пересечения прямых у = х и у = 5 – х . Решим уравнение:
х = 5 – х; 2 х = 5; х = 2,5.Значит, в треугольнике ОАВ АО = 5 и ВН = 2,5.
S = 

4. № 503. Р е ш е н и е
Построим искомый угол: 
V. Итоги урока. В о п р о с ы у ч а щ и м с я:
– Что называется решением неравенства с двумя переменными?
– Что называется решением системы неравенств с двумя переменными?
– Как решаются неравенства с двумя переменными?
– Как решаются системы неравенств с двумя переменными?
Домашнее задание: № 500 (б, г), № 501 (б), № 502 (а). Д о п о л н и т е л ь н о: № 557 (б).
Алгебра 9 класс Урок №___________________________________________________
Решение систем неравенств второй степени с двумя переменными
Тип урока: Урок закрепления знаний, ,формирование умений и навыков знаний.
формировать умение решать системы неравенств второй степени с двумя переменными.
Рассмотреть два способа решения систем неравенств (графический и аналитический способы) и научиться их решать, пользуясь алгоритмом
проконтролировать степень усвоения материала по теме.
способствовать развитию навыка самостоятельного применения знаний;
развивать навыки самоконтроля;
продолжить работу по развитию логического мышления и устной математической речи при поиске решения поставленной проблемы.
Воспитательные: приучать к умению общаться и выслушивать других;
воспитывать внимательность и наблюдательность;
стимулировать мотивацию и интерес к изучению математики.
Познавательные: осуществляют логические действия; формулируют ответы на вопросы.
Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения математических проблем, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения.
Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.
Личностные: проявляют способность к эмоциональному восприятию математатических объектов, задач, решений, рассуждений
Фронтальная (Ф); индивидуальная (И)
Оборудование: презентация, интерактивная доска, таблицы.
I. Организационный момент.
II. Устная работа. (по текстам ОГЭ)
III .Проверка домашней работы
IV .Закрепление навыков решения систем неравенств . № 577 (а).
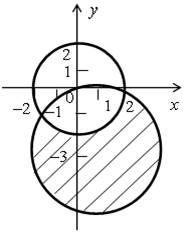
Неравенство х 2 + у 2 ≤ 25 задает круг с центром в начале координат и радиусом 5. Неравенство ху ≤ 0 задает вторую и четвертую координатные четверти.
На рисунке показано множество решений этой системы неравенств:
2. № 559 (б).Р е ш е н и е
х ( х 2 – у ) ≤ 0. Произведение двух выражений будет отрицательным, если эти выражения имеют разные знаки. То есть это неравенство равносильно совокупности двух систем:


VI .Домашняя работа__ № 500 (в), № 501( в), № 502 (б).
Д о п о л н и т е л ь н о: № 557 (в).
В о п р о с ы у ч а щ и м с я:
– Что называется решением неравенства с двумя переменными?
– Что называется решением системы неравенств с двумя переменными?
– Как решаются неравенства с двумя переменными?
– Как решаются системы неравенств с двумя переменными?
Алгебра 9 класс
Урок №_________________________Тема урока : Системы неравенств с двумя переменными.
обобщить и систематизировать знания учащихся по данной теме; закрепить умения решать уравнения, неравенства и их системы с двумя переменными
проконтролировать степень усвоения материала по теме.
способствовать развитию навыка самостоятельного применения знаний;
развивать навыки самоконтроля;
продолжить работу по развитию логического мышления и устной математической речи при поиске решения поставленной проблемы.
приучать к умению общаться и выслушивать других;
воспитывать внимательность и наблюдательность;
стимулировать мотивацию и интерес к изучению математики.
Познавательные: осуществляют логические действия; формулируют ответы на вопросы.
Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения математических проблем, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения.
Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.
Личностные: проявляют способность к эмоциональному восприятию математатических объектов, задач, решений, рассуждений
Фронтальная (Ф); индивидуальная (И)
I. Организационный момент.
II. Проверка домашней работы
III. Формирование умений и навыков. Предложить учащимся карточки-задания разного уровня сложности. Учащиеся выполняют решения самостоятельно, а учитель осуществляет контроль и в случае необходимости дает им консультации.
К а р т о ч к а № 1
1. Докажите, что пара чисел (–5; 2) не является решением системы уравнений
2. Решите систему уравнений:
а) 
3. Сумма двух чисел равна 25, а их произведение равно 144. Найдите эти числа.
4. Изобразите на координатной плоскости множество решений системы неравенств:
а) 
Р е ш е н и е заданий карточки № 1
1. Подставим х = –5 и у = 2 в каждое из уравнений системы:
2 · (–5) + 7 · 2 = 4;–10 + 14 = 4;4 = 4 – верно.
– 5 · 2 + 2 2 = 12;–10 + 4 = 12;–6 = 12 – неверно.
Значит, пара чисел (–5; 2) не является решением данной системы.
2.а)
х 2 – 2 х + 6 = 54; х 2 – 2 х – 48 = 0; х 1 = –6 

О т в е т: (–6; –9), (8; 5).
б)
2 – 4 у + у 2 = –1; у 2 – 4 у + 3 = 0;
у 1 = 1 
у 2 = 3 
О т в е т: (–1; 1), (–5; 3).
3. Обозначим первое число за х , а второе – за у . Согласно условию задачи получим систему уравнений:
25 у – у 2 = 144; у 2 – 25 у + 144 = 0;
D = 625 – 4 · 144 = 49;
у 1 = 

у 2 = 

О т в е т: 9 и 16.
а) 
К а р т о ч к а № 2
1. Решите систему уравнений:
а) 
2. Не выполняя построения, найдите координаты точек пересечения параболы у = 4 х 2 – 2 и прямой 3 х – 2 у = –1.
3. Произведение двух чисел на 13 больше их суммы. Если из первого числа вычесть утроенное второе число, то получится 9. Найдите эти числа.
4. Изобразите на координатной плоскости множество решений системы неравенств:
а) 
Р е ш е н и е заданий карточки № 2
1. а)
25 + 10 у + у 2 + 10 у + 2 у 2 – у 2 = –7; 2 у 2 + 20 у + 32 = 0;
у 2 + 10 у + 16 = 0; у 1 = –2 
у 2 = –8 
О т в е т: (3; –2), (–3; –8).
б)
10 х 2 = 50; х 2 = 5; х 1 = 


х 2 = – 


О т в е т: ( 



2. Чтобы найти координаты точек пересечения данных параболы и прямой, нужно решить систему уравнений:
3 х – 8 х 2 + 4 = –1; 8 х 2 – 3 х – 5 = 0;
х 1 = 1 
х 2 = 



О т в е т: (1; 2), 
3. Обозначим первое число за х , а второе – за у . Согласно условию задачи получим систему уравнений:
3 у 2 + 9 у = 4 у + 22; 3 у 2 + 5 у – 22 = 0; D = 25 + 264 = 289;
у 1 = 

у 2 = 


О т в е т: (15; 2), 
а) 
К а р т о ч к а № 3*
1. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют уравнению | у + 1 | = 2 – х .
2. Решите систему уравнений:
а) 
3. При смешивании первого раствора кислоты, концентрация которого 20 %, и второго раствора этой же кислоты, концентрация которого 50 %, получили раствор, содержащий 30 % кислоты. В каком отношении были взяты первый и второй растворы?
4. При каких значения параметра а система уравнений имеет два решения?
5. Изобразите на координатной плоскости множество решений системы неравенств:
Р е ш е н и е заданий карточки № 3*
1. Раскрывая модуль, получим совокупность двух уравнений:
1) если у ≥ –1, то у + 1 = 2 – х, у = 1 – х;
Изобразим на координатной плоскости оба этих случая:
а)
Сделаем замену: 

Складывая почленно левые и правые части уравнений этой системы, получим равенство:
Значит, система имеет бесконечное множество решений.
Выразим из второго уравнения переменную а через переменную b :
6 a – 4 b = 7; 6 a = 4 b + 7; a = 
Возвращаясь к замене, получим:
Получаем, что исходная система имеет бесконечное множество решений вида 

Например, это могут быть такие пары, как 
б)
Обозначим х + у = т , а ху = п . Тогда имеем:
х 2 + у 2 = ( х + у ) 2 – 2 ху = т 2 – 2 п . Получим систему:
т 1 = –10 
т 2 = 13 
Возвращаясь к замене, получим системы:
Решая эти системы, получаем ответ.
О т в е т: (6; 7), (7; 6), (–5 + 



3. Пусть было взято x г первого раствора и y г – второго раствора. По условию в первом растворе было 0,2 x г кислоты, а во втором – 0,5 y г кислоты.
После смешивания получили 30 %-ный раствор, то есть в нем было 0,3 ( x + y ) г кислоты. Масса кислоты после смешивания двух растворов равна сумме масс исходных растворов.
Получаем, что первый и второй растворы были взяты в отношении 2 : 1.
4.
Вычтем почленно из второго уравнения системы первое:
2 ху = 14 – 2 – 2 а;ху = 6 – а.
Тогда данную систему уравнений можно представить как совокупность двух систем:
1) 
Исходная система будет иметь два решения в трех случаях:
– если каждая из систем имеет по одному решению;
– если первая система имеет два решения, а вторая – решений не имеет;
– если вторая система имеет два решения, а первая – решений не имеет.
Если в каждой из полученных систем выразить одну переменную через другую и найти дискриминант, то в обоих случаях получим:
Выражение 4 а – 10 не может быть одновременно больше и меньше нуля, поэтому подходит тот случай, когда каждая из систем имеет единственное решение, то есть, когда D = 0:
5. 
( х – у ) ( х + у ) = 0
Для построения графика уравнения у = | х + 2 | необходимо раскрыть знак модуля и рассмотреть два случая.
Домашнее задание: № 527 (а, г), № 528 (а), № 529 (а), № 542, № 555.
Неравенство с двумя переменными и его решение: значение, список примеров
Содержание:
Линейное неравенство, имеющее две переменных; его функция имеет общий вид ах + bу + с меньше нулевого значения или больше 0. В качестве переменных выступают у, х. Для обозначения некоторых чисел используются буквы а, b, с. Решение неравенств с двумя переменными графическим способом предполагает использование плоскости координат. Задача – найти пару чисел, которая сделает пример верным равенством.
Неравенство с двумя неизвестными – сложный линейный пример, требующий построения графика. В большинстве случаев имеет множество вариантов решения. Например, заданы числа 2 и 1, необходимо решить выражение 5х + 2у > 4. Для этого следует подставить данные коэффициенты в пример. В итоге получается: 5*2 + 2*1 > 4, 10 + 2 больше 4. Решение допустимое.
Более легкий способ решить уравнение – построить графическую координатную плоскость. Внешний вид решения имеет определенную фигуру.
График неравенства с двумя переменными – решение
Функция имеет следующее определение: 3х — 2у + 6 > 0. Нужно определить точки на плоскости, которые подойдут для решения примера. Если 3х -2у + 6 > 0 приравнять к нулю, получится 3х — 2у + 6 = 0. Это стандартное обозначение прямой, проходящей через две области: -2,0 и 0,-3. Относим коэффициенты к области М1(Х1,У1). Эта зона заштриховывается на плоскости, она находится под 3х — 2у + 6 = 0 – прямой.
Коэффициенты М2(Х2,У2) попадают на прямую. Отсюда следует: 2у2 — 3х1 — 6 = 0, 2у1 — 3х1 — 6 0. Изначально строится прямая. В качестве решения выступает набор точек, расположенных над или под прямой. Чтобы понять, какая плоскость является ответом, необходимо выполнить подстановку значений в уравнение.
Графическое решение неравенств с двумя переменными – пример
Большинство неравенств с двумя неизвестными решаются графически. Необходимо выбрать, какой метод для поиска решения лучше применить. Координатная плоскость позволяет сделать рисунок, наглядно увидеть ответ. Задача – поиск двух коэффициентов, удовлетворяющих требованиям примера. Рассмотрим выражение 2у + 3х
http://infourok.ru/konspekti-urokov-po-algebre-v-klassah-po-teme-reshenie-sistem-neravenstv-s-peremennimikontrolnaya-rabota-po-teme-sistemi-uravnen-2517546.html
http://bingoschool.ru/manual/neravenstvo-s-dvumya-peremennyimi-i-ego-reshenie-znachenie-spisok-primerov/