Уравнение неразрывности для потока имеет

Уравнение неразрывности и уравнение Бернулли.

Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.

Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.

Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.

Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.

Содержание статьи

Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.

Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υ_ср .

Таким образом уравнение расхода для потока будет

υ_ср – средняя скорость потока

F – площадь сечения потока.

Уравнение неразрывности потока жидкости

Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.

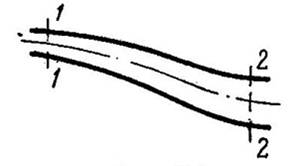
Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный

а через сечение 2-2 из него же вытекает объем, равный

Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.

Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.

Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки

Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что

т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.

Уравнение неразрывности струи жидкости. Уравнение Бернулли.

Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.

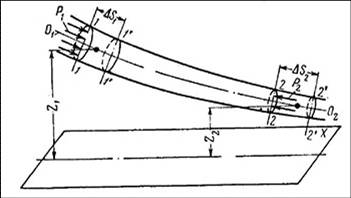
При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.

Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.

Если всё это записать в виде формулы, то

где W – приращение кинетической энергии = m * υ 2 / 2

ΣA – сумма работ действующих сил = P *ΔS

В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.

Теперь рассмотрим обе части этого выражения по порядку.

Приращение кинетической энергии ΔW

В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.

Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.

Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен

масса в этом случае получается равной

Подставляя все это в выражение для кинетической энергии получаем цепочку

ΔW = m * υ 2 ₂ / 2 — m * υ 2 ₁ / 2 = ρ * q * ΔТ * υ 2 ₂ / 2 — ρ * q * ΔТ * υ 2 ₁ / 2

Работа сил действующих на систему ΣA

Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести A_Т равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.

Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.

Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.

Силы давления А_Д , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.

Суммарно работа сил давления будет

Подставляя в начальное уравнение

Полученные выражения для ΔW и ΣA получаем

Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые

Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:

Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2

В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Видео по теме уравнение неразрывности

Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.

Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.

Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.

Гидродинамика. Уравнение неразрывности движения жидкости.

Уравнение неразрывности потока демонстрирует закон сохранения массы: количество втекающей и вытекающей жидкости неизменно.

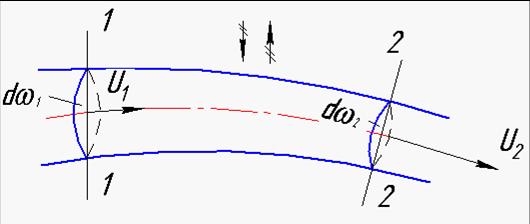
Проанализируем сечение 1 с площадью и скоростью движения частиц жидкости обозначим и₁. Элементарный расход для него представлен соотношением:

Далее проанализируем сечение 2 в этой же струйке с площадью сечения и скоростью обозначим и₂. Элементарный расход для него представлен соотношением:

Но согласно характерной особенности элементарной струйки притока и оттока жидкости через ее боковую поверхность не существует; на промежутке 1 — 2, которому свойственны постоянные размеры, отсутствуют пустоты и отсутствуют переуплотнения количества жидкости, протекающей в единицу времени сквозь сечения 1 и 2,будут одинаковыми, тогда:

Уравнение неразрывности для элементарной струйки — элементарный расход жидкости при установившемся движении величина одинаковая для всей элементарной струйки.

Проанализируем трубу с переменным живым сечением. Расход жидкости через трубу для всякого ее сечении постоянен, т.е. Q₁=Q₂= const, делаем вывод:

Значит, когда течение в трубе сплошное и неразрывное, то уравнение неразрывности станет:

Найдем отсюда скорость для выходного сечения:

Обратим внимание, что скорость возрастает обратно пропорционально площади живого сечения потока. Указанная обратная зависимость между скоростью и площадью выступает важным следствием уравнения неразрывности и нашла широкое применение. Так, к примеру, эта особенность используется пожарными при тушении пожара для формирования сильной и дальнобойной струи.

Что произойдет со скорость потока при сужении, когда диаметр напорной трубы d сузиться в два раза?

Площадь живого сечения трубы вычисляем на основе формулы w = πd 2 / 4. В этом случае соотношение площадей в формуле u₂ = u₁ w₁ / w₂ равняться 4.

Следовательно, в ситуации, когда диаметр трубы сужается в два раза — скорость потока возрастет в четыре раза. По аналогии, когда диаметр сузится в три раза — скорость увеличиться в девять раз.

Уравнение неразрывности для потока имеет

Уравнение неразрывности потока жидкости. Уравнение Бернулли

1. Уравнение неразрывности потока жидкости

Вооружившись основными понятиями получим уравнение неразрывности потока

Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный

а через сечение 2-2 из него же вытекает объем, равный

Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.

Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.

Такие соотношения можно составить для любых двух сечений струйки.

Поэтому в более общем виде получаем, что всюду вдоль струйки

Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики.

Переходя далее к потоку жидкости в целом получаем, что

т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений .

Для трубки переменного сечения

а) Для элементарной струйки

В элементарной струйке переменного сечения выберем два произвольных сечения 1-1 и 2-2 с живыми сечениями dw ₁ и dw ₂ . Так как жидкость является сплошной средой (без пустот и переуплотнений) и приток и отток жидкости вдоль струйки отсутствуют, то для несжимаемой жидкости можно предположить, что объемные расходы через сечения 1-1 и 2-2 должны быть равны между собой:

уравнения (1), (2) называют уравнениями неразрывности, или сплошности.

Из уравнения (2) можно получить:

Аналогичное уравнение можно составить и для потока, ограниченного непроницаемыми стенками, только вместо истинных скоростей ввести средние скорости:

2. Вывод уравнения Бернулли

Вторым основным уравнением гидродинамики является уравнение Бернулли , устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.

При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.

Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.

Если всё это записать в виде формулы, то ΔW = ΣA,

где W – приращение кинетической энергии = m*υ 2 /2

ΣA – сумма работ действующих сил = P *ΔS

В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.

Теперь рассмотрим обе части этого выражения по порядку.

1) Приращение кинетической энергии ΔW

В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.

Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.

Вспоминая, что по условию неразрывности расход ( Q или q ) во всех сечениях элементарной струйки одинаков, а следовательно будет равен V= q · ΔТ

масса в этом случае получается равной m =ρ · q · ΔТ

Подставляя все это в выражение для кинетической энергии получаем цепочку

2) Работа сил действующих на систему ΣA

Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести A_Т равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.

Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z₁ –Z₂.

где Z₁ и Z₂ – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.

Силы давления А_Д, действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.

Суммарно работа сил давления будет

Подставляя в начальное уравнение ΔW = ΣA,

Полученные выражения для ΔW и ΣA получаем

Разделим обе части этого уравнения на m = ρ · q · ΔТ и перегруппируем слагаемые

Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:

Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки.

Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ρ
Кинетическая удельная энергия = υ 2 / 2

Разделим последнее уравнение на ускорение свободного падения и получим:

В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

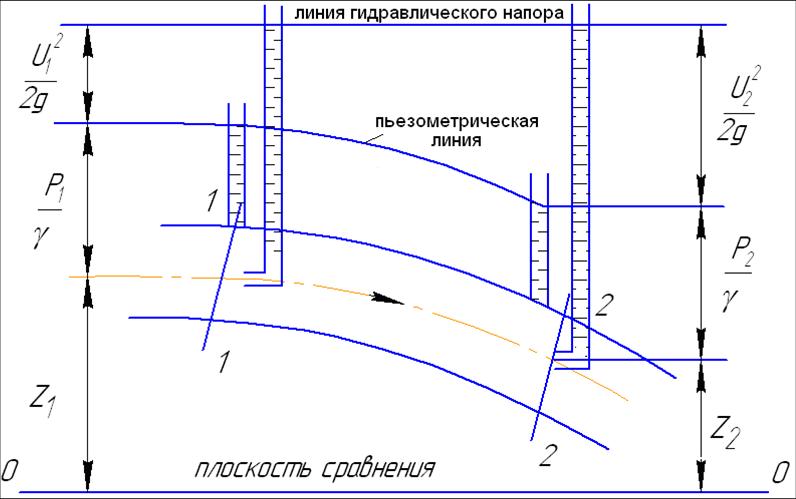
Z – геометрический напор, или удельная потенциальная энергия положения;

— пьезометрический напор, или удельная потенциальная энергия давления;

— скоростной напор, или удельная кинетическая энергия.

Сумма всех напоров составляет гидродинамический напор:

Физический смысл уравнения Бернулли заключается в том, что оно является уравнением закона сохранения энергии для движущейся жидкости.

Для лучшего понимания смысла полученного уравнения представим его графически.

3. Порядок применения уравнения Бернулли для гидравлических расчетов .

С помощью уравнения Бернулли решается большинство задач практической гидравлики.

Для этого выбирают два сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ, g, а для другого сечения одна или величины подлежали определению.

При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости υ₁ω ₁ = υ₂ω₂.

Условие применения уравнения Бернулли.

Уравнение Бернулли справедливо, если:

1. C корость во времени не изменяется,

2. Расход постоянный,

3. Движение изменяется плавно,

4. Между сечениями нет притока или стока энергии.

Решение задач на уравнение на разрывности

Задача 1. Определить расход потока и среднюю скорость в сечениях с площадями ω₁ = 0,6 м 2 , ω₂ = 0,8 м 2 , если в живом сечении с площадью ω₃ = 0,5 м 2 средняя скорость v ₃ = 0,88 м/с;

Задача 2. Вода течет в горизонтально расположенной трубе переменного сечения. Скорость v₁ воды в широкой части трубы равна 20 см/с. Определить скорость v₂ в узкой части трубы, диаметр d₂ которой в 1,5 раза меньше диаметра d₁ широкой части.

Задача 3 Горизонтальный цилиндр насоса имеет диаметр d₁=20 см. В нем движется со скоростью v₁=1 м/с поршень, выталкивая воду через отверстие диаметром d₂=2 см. С какой скоростью v₂ будет вытекать вода из отверстия?

Задача 4. Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда S₁, сечение струи S₂. Найдите ускорение, с которым перемещается уровень воды в сосуде.

Задача 5. Скорость в сечении 1 равна 0,8 м/с, диаметр трубы в сечении 1 равен d₁ = 50 мм, а сечении 2 d₂ = 100 мм. Определить скорость в сечении 2.

Решение задач на уравнение Бернулли

Задача 1. В широкой части горизонтально расположенной трубы нефть течет со скоростью v₁=2 м/с. Определить скорость v₂ нефти в узкой части трубы, если разность Δp давлений в широкой и узкой частях ее равна 6,65 кПа.

Задача 2. В горизонтально расположенной трубе с площадью S₁ поперечного сечения, равной 20 см 2 , течет жидкость. В одном месте труба имеет сужение, в котором площадь S₂ сечения равна 12 см 2 . Разность Δh уровней в двух манометрических трубках, установленных в широкой и узкой частях трубы, равна 8 см. Определить объемный расход Q_V жидкости.

Задача 3. Горизонтальный цилиндр насоса имеет диаметр d₁=20 см. В нем движется со скоростью v₁=1 м/с поршень, выталкивая воду через отверстие диаметром d₂=2 см. С какой скоростью v₂ будет вытекать вода из отверстия? Каково будет избыточное давление p воды в цилиндре?

Задача 4 Определить скорость истечения жидкости из отверстия в открытом сосуде,

Задачи для самостоятельного решения:

Задача 1. К поршню спринцовки, расположенной горизонтально, приложена сила F=15 Н. Определить скорость v истечения воды из наконечника спринцовки, если площадь S поршня равна 12 см 2 .

Задача 2 Струя воды диаметром d=2 см, движущаяся со скоростью v=10 м/с, ударяется о неподвижную плоскую поверхность, поставленную перпендикулярно струе. Найти силу F давления струи на поверхность, считая, что после удара о поверхность скорость частиц воды равна нулю.

Задача 3. Определить расход потока и среднюю скорость в сечениях с площадями ω₁ = 0,6 м 2 , ω₂ = 0,8 м 2 , если в живом сечении с площадью ω₃ = 0,5 м 2 средняя скорость V₃: а) 0,95 м/с; б) 1,05 м/с; в) 1,13 м/с; г) 1,25 м/с.

Задача 4 Струя воды с площадью S₁ поперечного сечения, равной 4 см 2 , вытекает в горизонтальном направлении из брандспойта, расположенного на высоте H =2 м над поверхностью Земли, и падает на эту поверхность на расстоянии l =8 м. Пренебрегая сопротивлением воздуха движению воды, найти избыточное давление p воды в рукаве, если площадь S₂ поперечного сечения рукава равна 50 см 2 ?

1. Объясните смысл удельной энергии жидкости?

2. Как выглядит уравнение Д.Бернулли для потока вязкой жидкости?

3. При каких условиях возможно применение уравнения Д.Бернулли для гидравлических расчетов?

4. Запишите у равнение неразрывности течений

5. Запишите уравнение Бернулли для идеальной жидкости

6. Член уравнения Бернулли, обозначаемый буквой z, называется

7. Член уравнения Бернулли, обозначаемый выражением называется

8. Член уравнения Бернулли, обозначаемый выражением называется

9. Между какими параметрами уравнение Бернулли для двух различных сечений потока дает взаимосвязь

10. Коэффициент Кориолиса в уравнении Бернулли характеризует