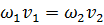Уравнение неразрывности движущейся жидкости для установившегося движения

Уравнение неразрывности (или сплошности) движущейся жидкости в случае установившегося движения

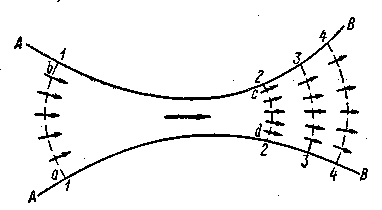
1°. Случай резко изменяющегося движения жидкости. Представим на рис. 3-14 поток (струю) жидкости и наметим два его живых сечения 1—1 и 2—2. Рассмотрим отсек abed, заключенный между этими сечениями и ограни­ченный с боков поверхностью АВ, образованной линиями тока. Будем счи­тать, что этот

отсек принадлежит пространству и является неподвижным,жидкость же протекает через него.

Рис. 3-14. К выводу уравнения (3-38)

Обозначим через Q₁ и Q₂ расходы соответственно для сечений 1—1 и 2—2. За время dt в отсек abcd через живое сечение 1—1поступит объем жидкости, равный Qxdt; за это же время через живое сечение 2—2 из отсека abcd выйдет объем жидкости, равный Q₁dt. Учтем следующие три обстоятель­ства:

1) проникновение жидкости через боковую поверхность АВ отсека abcd невозможно, так как эта поверхность образована линиями тока (траектория­ми) вдоль которых одна за другой движутся частицы жидкости:

2) жидкость является несжимаемой;

3) жидкость движется сплошным потоком, без образования в нем разры­вов (ограничимся рассмотрением только такого случая; вопросов кавитации, аэрации потока и т. п. [см. § 1-5] здесь касаться не будем).

Имея в виду эти три обстоятельства, можем утверждать, что объем жид­кости Q_xdt должен быть равен объему жидкости Q₂dt:

Помимо сечений 1—1 и 2—2, можно наметить целый ряд других живых сечений: 3—3, 4—4 и т. д. Рассматривая все эти сечения так же точно, как и сечения 1—1 и 2—2, можно прийти к выводу, что

Q= const (вдоль потока). (3-38)

Как видно, если жидкость движется без образования разрывов, то при установившемся движении расход Q для всех живых сечений потока (ограни­ченного с боков линиями тока, т. е. при условии отсутствия бокового притока или оттока жидкости) одинаков.

Уравнение (3-38) и является искомым уравнением. Оно отражает свой­ства несжимаемости (см. выше п. 2) и н е р а з р ы в н о с т и, дру­гими словами, сплошности (см. выше п. 3) движущейся жидкости. Поэтому данное уравнение следовало бы называть уравнением несжимаемости и неразрывности (сплошности) движущейся жидкости. Мы, однако, будем далее именовать его просто уравнением неразрывности.

Заметим, что уравнение (3-38) можно распространить и на любые поперечные сечения потока (не обязательно только на его живые сечения); важно только, чтобы при поясненных выше условиях (см. пп. 1—3) рассматриваемые сечения полностью пересекали данный поток жидкости. При этом уравнение (3-38) можно переписать в виде: Q = const (для всех по­перечных сечений потока), где Q — объем жидкости, проходящей в единицу времени через любое поперечное сечение потока.

2°. Случай плавно изменяющегося и параллельноструйного движений жидкости. В этом случае оперируют плоскими живыми сечениями, причем величину Q выражают зависимостью (3-32). Имея это в виду, для плавно изме­няющегося и параллельноструйного движений уравнение неразрывности (3-38) можно представить еще в виде

= const (вдоль потока), (3-39)

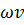
откуда получаем:

(3-40)

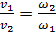
Как видно, средние скорости обратно пропорциональны площадям живых сечений потока.

Если бы вместо целого потока жидкости мы рассматривали только эле­ментарную струйку его, то уравнения (3-39) и (3-40) для такой струйки следовало бы переписать в виде.

(вдоль струйки); (3-41)

(3-42)

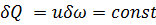
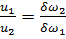
Уравнение неразрывности и уравнение Бернулли.

Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.

Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.

Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.

Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.

Содержание статьи

Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.

Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υ_ср .

Таким образом уравнение расхода для потока будет

υ_ср – средняя скорость потока

F – площадь сечения потока.

Уравнение неразрывности потока жидкости

Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.

Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный

а через сечение 2-2 из него же вытекает объем, равный

Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.

Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.

Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки

Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что

т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.

Уравнение неразрывности струи жидкости. Уравнение Бернулли.

Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.

При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.

Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.

Если всё это записать в виде формулы, то

где W – приращение кинетической энергии = m * υ 2 / 2

ΣA – сумма работ действующих сил = P *ΔS

В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.

Теперь рассмотрим обе части этого выражения по порядку.

Приращение кинетической энергии ΔW

В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.

Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.

Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен

масса в этом случае получается равной

Подставляя все это в выражение для кинетической энергии получаем цепочку

ΔW = m * υ 2 ₂ / 2 — m * υ 2 ₁ / 2 = ρ * q * ΔТ * υ 2 ₂ / 2 — ρ * q * ΔТ * υ 2 ₁ / 2

Работа сил действующих на систему ΣA

Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести A_Т равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.

Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.

Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.

Силы давления А_Д , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.

Суммарно работа сил давления будет

Подставляя в начальное уравнение

Полученные выражения для ΔW и ΣA получаем

Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые

Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:

Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2

В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Видео по теме уравнение неразрывности

Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.

Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.

Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.

Гидродинамика. Уравнение неразрывности движения жидкости.

Уравнение неразрывности потока демонстрирует закон сохранения массы: количество втекающей и вытекающей жидкости неизменно.

Проанализируем сечение 1 с площадью и скоростью движения частиц жидкости обозначим и₁. Элементарный расход для него представлен соотношением:

Далее проанализируем сечение 2 в этой же струйке с площадью сечения и скоростью обозначим и₂. Элементарный расход для него представлен соотношением:

Но согласно характерной особенности элементарной струйки притока и оттока жидкости через ее боковую поверхность не существует; на промежутке 1 — 2, которому свойственны постоянные размеры, отсутствуют пустоты и отсутствуют переуплотнения количества жидкости, протекающей в единицу времени сквозь сечения 1 и 2,будут одинаковыми, тогда:

Уравнение неразрывности для элементарной струйки — элементарный расход жидкости при установившемся движении величина одинаковая для всей элементарной струйки.

Проанализируем трубу с переменным живым сечением. Расход жидкости через трубу для всякого ее сечении постоянен, т.е. Q₁=Q₂= const, делаем вывод:

Значит, когда течение в трубе сплошное и неразрывное, то уравнение неразрывности станет:

Найдем отсюда скорость для выходного сечения:

Обратим внимание, что скорость возрастает обратно пропорционально площади живого сечения потока. Указанная обратная зависимость между скоростью и площадью выступает важным следствием уравнения неразрывности и нашла широкое применение. Так, к примеру, эта особенность используется пожарными при тушении пожара для формирования сильной и дальнобойной струи.

Что произойдет со скорость потока при сужении, когда диаметр напорной трубы d сузиться в два раза?

Площадь живого сечения трубы вычисляем на основе формулы w = πd 2 / 4. В этом случае соотношение площадей в формуле u₂ = u₁ w₁ / w₂ равняться 4.

Следовательно, в ситуации, когда диаметр трубы сужается в два раза — скорость потока возрастет в четыре раза. По аналогии, когда диаметр сузится в три раза — скорость увеличиться в девять раз.