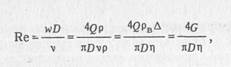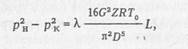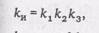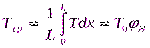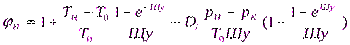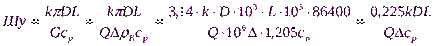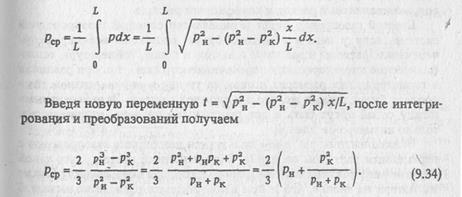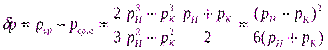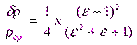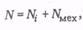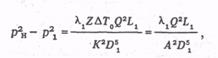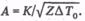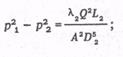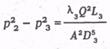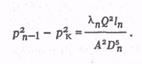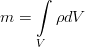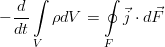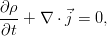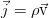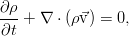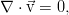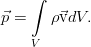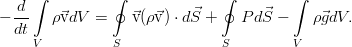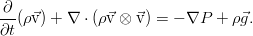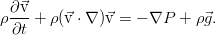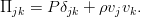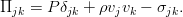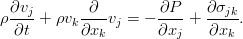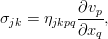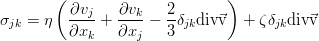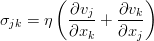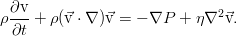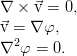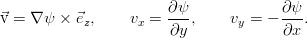Уравнение неразрывности и уравнение движения газа

Неразрывности и уравнение движения.

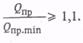
Глава 9. ТЕХНОЛОГИЧЕСКИЙ РАСЧЕТ МАГИСТРАЛЬНЫХ

§41. Уравнение неразрывности и уравнение движения

При установившемся режиме в трубопроводе постоянного (или переменного) сечения и без отбора (прихода) газа по длине количество газа (массовый расход), проходящее через любое поперечное сечение трубы, во времени остается постоянным, т.е.

(9.1)

где р — плотность газа; F — площадь поперечного сечения трубопровода; w — средняя скорость течения газа; индексы 1 и 2 относятся соответственно к первому и второму произвольным сечениям.

Это уравнение справедливо для всех газопроводов. При небольших рабочих давлениях (городские газовые сети) плотность газа меняется незначительно и для технических расчетов ее можно принять постоянной, т.е. считать газ несжимаемой средой. Тогда уравнение неразрывности упрощается и имеет вид

(9.2)

где Q — объемный расход газа.

При движении газа вследствие преодоления гидравлических сопротивлений происходит значительное падение давления по длинетрубопровода. В этих условиях плотность газа по длине трубопровода будет уменьшаться, что приведет к изменению скорости течения газа (в трубопроводе постоянного диаметра скорость течения газа по длине возрастает). Поэтому для газового потока уравнение баланса удельной энергии можно записать только в дифференциальной форме

(9.3)

Для магистральных трубопроводов можно пренебречь силами инерции d(w 2 )/2 и разностью геодезических высот gdz.

Рассмотрим установившееся изотермическое течение газа в трубопроводе постоянного диаметра и в качестве дополнительных уравнений используем уравнение состояния для реального газа

(9.5)

уравнение Дарси — Вейсбаха для потерь на трение

(9.6)

(9.7)

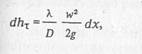
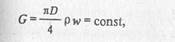
где Т₀ = соnst — температура газа (температура окружающей среды); х— продольная координата для произвольного сечения; F = πD 2 /4; D -внутренний диаметр трубопровода.

Подставляя выражения (9.5), (9.6) и (9.7) в равенство (9.4), получаем

Коэффициент гидравлического сопротивления λ в общем случаезависит от числа Рейнольдса Rе и шероховатости внутренней поверхности трубы. Для конкретного трубопровода шероховатость труб является вполне определенной величиной; посмотрим, как ведет себя параметр Rе, а именно

где ρ_в — плотность воздуха; ∆ — относительная плотность газа.

Так как динамическая вязкость η зависит от температуры и практически не зависит от давления, то отсюда следует, что параметр Rе по длине не меняется. Следовательно, коэффициент гидравлического сопротивления λ, несмотря на существенное изменение скорости течения газа w по длине трубопровода, для изотермического установившегося потока газа остается постоянной величиной.

Проинтегрировав уравнение (9.8) по давлению от р_н до р_к и по длине от х=0 до х=L, получим

где р_н, р_к — давление соответственно в начале и конце газопровода; L — длина газопровода.

Последнее выражение чаще представляют в виде формулы массового расхода

(9.9)

При проектировании и эксплуатации газопроводов понятие массовый расход практически никогда не используют; вместо него применяют объемный расход, приведенный к стандартным условиям. Этот расход называют также коммерческим (слова «при стандартных. условиях» или «коммерческий» практически всегда в технической документации .опускаются как само собой разумеющиеся). На основании уравнения состояния, а также с учетом ∆ = R/R_В, объемный (коммерческий) расход

(9.10)

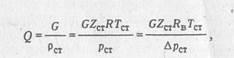
где p_СT — плотность газа при стандартных условиях (р_ст, T_СT); R_в — газовая постоянная воздуха; ∆ — относительная плотность газа по воздуху;

Z_СТ = 1 — коэффициент сжимаемости газа при стандартных условиях.

На основании выражений (9.9) и (9.10) получим

Лекция № 9. Практические формулы для гидравлического расчета газопровода.

§ 42.Практические формулы

для гидравлического расчета газопровода

Если задана годовая пропускная способность Q_Г магистрального газопровода, то расчетная суточная пропускная способность

(9.12)

где k_и — оценочный коэффициент использования пропускной способности,

где k₁ — коэффициент повышенного спроса газа, k₁ =0,95, k₂ — коэффициент экстремальных температур k₂=0,98 , k₃ – коэффициент надежности, учитывающий отказы линейной части и оборудования КС магистрального газопровода, k₃ принимают по ОНТП 51 -1 – 85 в зависимости от диаметра и длины газопровода и установленного оборудования на КС.

Для сложных газотранспортных систем k_и =0,875+0,92.

Гидравлический расчет отводов и распределительных газопроводов проводят по максимальному часовому и максимальному суточному потреблению таза, соответственно.

Расчетная пропускная способность газопровода (в млн.: м 3 /сут ) выражается следующей зависимостью

(9.13)

где D — внутренний диаметр трубы; р_н, р_к — давление соответственно в начале и конце газопровода; λ- коэффициент гидравлического сопротивления; ∆ — относительная плотность газа по воздуху; Z – средний коэффициент сжимаемости газа; Т_ср — средняя по длине газопровода температура транспортируемого газа; L — длина газопровода.

Расчетный коэффициент гидравлического сопротивления для магистральных газопроводов в основном зависит от коэффициента гидравлического сопротивления от трения λтр, определяемого в свою очередь по универсальной (обобщенной) формуле ВНИИГаза

(9.14)

Где Rе — число Рейнольдса; k_э — эквивалентная шероховатость внутренней поверхности труб.

В такой форме выражение (9.14) применимо для зоны смешанного трения. При гладкостенном (гидравлически гладкие трубы) режиме течения газа, когда 158/Rе >>2k_э/D формула (9.14) будет иметь вид

При квадратичном законе сопротивления, когда 158/Rе Rе_пер имеем квадратичный режим течения, при Rе расхода и коэффициента гидравлического сопротивления.

Значения Q_ф и λ_ф вычисляют по формулам (9.13) и (9.22), подставляя в них замеренные данные всех параметров. Измерения делают в дни, когда режим перекачки наиболее близок к стационарному.

Коэффициент эффективности определяют периодически для каждого участка (перегона между КС).

Физические параметры газа, необходимые для гидравлического расчета, определяют при средних по длине расчетного участка давлении и температуре газа.

Если целью гидравлического расчета является определение значений Q или D, то предварительно расчет их проводят по формулам для квадратичного режима течения газа, а затем уточняют режим течения. Если Q > Q_пер, то режим квадратичный; если же Q 2 _к применять р 2 _к ·ехр [а (z_к — z_н)] , а в знаменатель под радикалом ввести множитель φ_нг

Анализ показывает, что рельеф следует учитывать, если разность отметок отдельных точек трассы превышает 200 м в сравнении с началом газопровода. При этом, при сравнительно спокойном рельефе (приближающемся к наклонному газопроводу) можно пользоваться формулой (9.25), а при сложных рельефах — формулой (9.27).

44. Влияние неизотермичности потока на пропускную способность газопровода

При выводе формулы (9.9) предполагали изотермическое установившееся течение газа по трубопроводу при температуре окружающей

среды Т₀ = соnst. На самом же деле газ при прохождении через компрессоры нагревается и, несмотря на то, что после его охлаждают, при поступлении в трубопровод он имеет температуру 310-340 К, существенно отличающуюся от температуры окружающей среды. По мере удаления от КС газ остывает. Опыт показывает, что лишь на расстоянии 20-30 км от КС температура газа становится близкой к температуре окружающей среды и так будет после каждой КС. Кроме этого, необходимо учитывать, что по трубопроводу движется реальный газ, которому присущ эффект Джоуля — Томсона (при расширении реального газа температура его падает, а при сжатии — возрастает). Таким.образом, в любом газопроводе движение газа будет всегда неизотермическим. Поэтому в практические расчетные зависимости (9.13) и (9.22) вместо Т₀ введена средняя температура газового потока на перегоне между смежными КС Т_ср.

На основании выражения (9.28) имеем

где φ_н — поправка на неизотермичность потока.

Если для расчетовприменять практически удобные единицы физических величин: Q, млн.м 3 /сут; D, мм; L,км; k, Вт/(м 2 ·К); с_р ,Дж/(кг·К);ρ_в =1,105кг/м 3 ,то

Где k – коэффициент теплопередачи от газа к грунту. Ориентировочно можно принимать для грунта , состоящего из сухого песка, k=1,2Вт/(м 2 ·К),для очень влажного песка k=3,5Вт/(м 2 ·К), для сыроватой глины k=1,6 Вт/(м 2 ·К). При отсутствии данных о характере и влажности грунта по трассе газопровода коэффициент теплопередачи принимают равным 1,75Вт/(м 2 ·К). Для природных газов в расчетах коэффициента Джоуля-Томсона D_i =3-3,5 К/МПа.

Найденное таким образом значение Шу подставляют в формулы (9.28) и (9.30).

Если искомыми величинами являются Q,D и L, то в формулах расхода (9.13) и (9.22) предварительно используют ориентировочное значение Tср, в качестве которого рекомендуется принимать Tср= 1/3T_н+ 2/3T₀.

Затем по полученным величинам Q,D и L по формуле (9.30) определяют T_ср. Расчетное значение средней температуры не должно отличаться от ориентировочно принятого более чем на 5 К. При большем отклонении проводят повторный расчет при новом ориентировочном значении Тср.

Лекция№11. Изменение давления по длине газопровода.

45.Изменение давления по длине газопровода

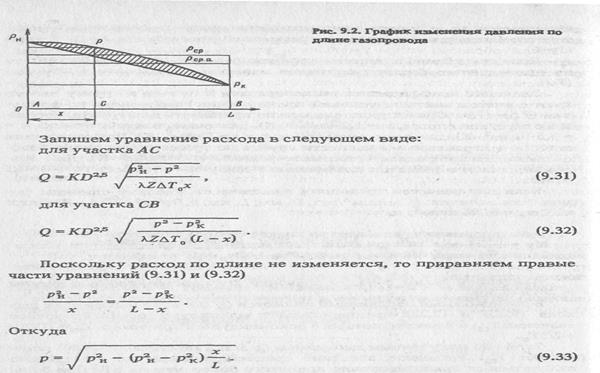
Рассмотрим участок магистрального газопровода длиной -L, между смежными КС с давлением в начале р_н и в конце участка р_к. Необходимо определить давление в точке С на расстоянии х от начала (рис.9.2). Для этого можно воспользоваться формулой расхода в любом виде, например, (9.9), (9.11), (9.13), (9.22).

Линия, описываемая уравнением (9.33), является параболой. Из характера этой кривой видно (см. рис. 9.2), что градиент давления увеличивается по длине газопровода, т.е. гидравлический уклон, в отличие от нефтепроводов не постоянен. В начале газопровода, когда давление высокое, плотность газа велика. Вследствие этого удельный объем газа мал и скорость движения газа небольшая. По мере удаления от начала трубопровода давление газа уменьшается. При уменьшении давления увеличивается удельный объем газа и, следовательно, при постоянном диаметре трубы увеличивается скорость газа, что ведет к росту потерь давления на трение, пропорциональных квадрату скорости. С увеличением расстояния от КС растет падение давления, приходящееся на единицу длины трубопровода, а следовательно,

растут потери энергии, связанные с перемещением газа.Таким образом, чтобы уменьшить затраты энергии на перекачку газа — одна из основных статей эксплуатационных расходов на газопроводах — целесообразно расстояние между КС сокращать. Однако при уменьшении длины перегонов между станциями растет необходимое число КС, а следовательно, возрастают капитальные затраты на сооружение их и связанные с ними эксплуатационные расходы. Оптимальное расстояние между станциями и оптимальный перепад давлений на перегоне определяют исходя из экономических соображений сучетом вышеназванных противодействующих друг другу факторов. Для КС с центробежными нагнетателями при существующих единичных стоимостных показателях оптимальное конечное давление Р_к получается около 3 МПа при давлении в начале перегона Р_н = 5,6 МПа и P_к = 4,5 — 5 МПа при Р_н = 7,6 МПа. Для КС с поршневыми компрессорами оптимальная степень сжатия равна ε = р_н/р_к = 2,2 при р_н = 5,5 МПа.

§ 46. Среднее давление в газопроводе

Чтобы определить коэффициент сжимаемости, необходимо знать среднее давление в газопроводе. Кроме того, среднее давление необходимо для определения количества газа, заключенного в объеме трубопровода, для расчета аккумулирующей способности участка газопровода и т.д.

Так как закон изменения давления по длине газопровода нелинейный (см. рис. 9.2), то среднее давление необходимо определять как среднее интегральное значение.

Иногда вместо среднего интегрального Р_ср применяют среднее арифметическое давление Р_ср._а, которое меньше среднего интегрального на величину, пропорциональную заштрихованной площади (см. рис.9.2). При этом абсолютная погрешность

А относительная погрешность

Чем больше степень сжатия ε, тем больше относительная погрешность (разумеется и абсолютная) от применения среднего арифметического давления. Так, при ε=2, наиболее близкой к реальным значениям на магистральных газопроводах δр/р_ср =3,6 % ; при ε=3 погрешность уже составляет 7,7 % ; предельная погрешность – 25% (при ε→∞).

профиле по горизонтали, а превышения откладывают в вертикальноммасштабе по вертикали. Поэтому для определения по профилю расстояния между двумя пунктами трассы на местности надо измерить напрофиле расстояние между ними по горизонтали и, пользуясь коэффициентом горизонтального масштаба, вычислить истинное расстояние между пунктами

Лекция№12. Расчет режимов работы

Магистральных газопроводов

§ 50. Расчет режимов работы магистральных газопроводов

Режимы работы КС с центробежными нагнетателями рассчитывают по приведенным газодинамическим характеристикам одного или группы (с учетом соединения) нагнетателей, составленных ВНИИгазом по данным испытаний. На рис. 9.6 в качестве примера показана приведенная газодинамическая характеристика нагнетателя Н-300-1,23 с рабочим колесом диаметром 782 мм, номинальной частотой вращения n_н = 6150 об/мин, подачей 19 млн. м 3 /сут и оптимальной степенью сжатия 1,27. На графике показаны зависимости степени сжатия ε, политропического к.п.д. η_пол и приведенной относительной внутренней мощности (N_i / ρ_в)_пр от приведенной объемной подачи Q_Пр. При построении характеристики нагнетателя были приняты наиболее часто встречающиеся значения приведенных параметров: газовой постоянной R_пр = 490,5 Дж/(кг • К); коэффициента сжимаемости газа Z_пр = 0,91; температура газа на входе в нагнетатель (Т_в)_пр = 288 К. Исходными величинами для расчета режима работы нагнетателя являются: n -рабочая частота вращения колеса нагнетателя; р_в — абсолютное давление газа перед нагнетателем; T_в — температура газа перед нагнетателем; Q_к — коммерческая подача нагнетателя при стандартных условиях (для группы нагнетателей Q_К делят на число параллельно работающих нагнетателей или групп нагнетателей); ∆ — относительная плотность газа по воздуху или абсолютная плотность газа при стандартных условиях.

Рабочие параметры нагнетателя определяют в следующей последовательности.

. Рис. 9.6. Газодинамическая характеристика центробежного

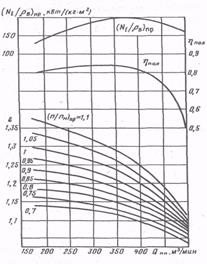
1. По известным давлению и температуре перед нагнетателем и составу газа находят коэффициент сжимаемости Z.

2. Определяют плотность газа ρ_в и подачу нагнетателя Q в условиях перед нагнетателем, а также газовую постоянную газа R =R_B /∆ = 287,1/∆ Дж/кг·К).

3. Вычисляют значение приведенной подачи нагнетателя по формуле

(9.84)

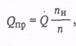
где n_н — номинальная частота вращения колеса нагнетателя.

4. Определяют приведенную частоту вращения по формуле

(9.85)

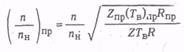
5. Из приведенных характеристик по значениям Q_пр и (n/n_н)_пр устанавливают необходимую степень сжатия ε.

6. По значению Q_пр также из приведенных характеристик определяют к.п.д. η_пол и удельную внутреннюю мощность (N_i/ρ_в)_пр.

7. Определяют внутреннюю мощность, потребляемую нагнетателем, по формуле

(9.86)

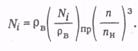
8. Мощность на валу привода нагнетателя

Где N_мех — механические потери, принимаемые 100 кВт для газотурбинного привода и 150 кВт для электропривода.

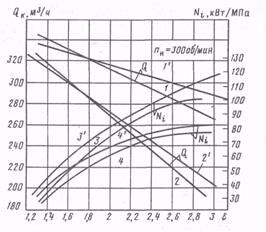
9. Определяют удаленность режима работы нагнетателя от границы помпажа, т.е. проверяют соблюдение условия

10. Определяют температуру газа на выходе из нагнетателя по

(9.89)

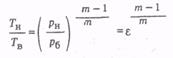
где m — показатель политропы (адиабаты), для природных газов меняется в пределах 1,25-1,4, в среднем m = 1,32; индексы «в» и «н» относятся соответственно к входному и нагнетательному патрубку ГПА.

Режим работы КС с газомоторными компрессорами рассчитывают по так называемым загрузочным кривым. Пример загрузочной кривой для газомотокомпрессоров типов 10ГК представлен на рис. 9.7.

По степени сжатия газа на КС ε определяют объемную подачу Q_к одного цилиндра компрессора при условиях перед станцией, в затем пересчитывают ее на стандартные условия. По числу компрессорных цилиндров агрегата определяют объемную подачу компрессора. После этого по заданной пропускной способности трубопровода и подаче одного компрессора находят число компрессоров, которое округляют в большую сторону. По полученному числу компрессорных агрегатов определяют необходимую подачу одного компрессора (одного цилиндра) и затем по загрузочным кривым устанавливают число открытых регуляторов (карманов) или степень снижения частоты вращения вала агрегата. По загрузочным кривым находят внутреннюю удельную мощность компрессора N_i, а потребляемую компрессором мощность рассчитывают следующим образом

(9.90)

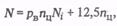
Рис. 9.7. Загрузочные кривые одного компрессорного цилиндра диаметром 197 мм, оборудованного прямоточными (1—4) и кольцевыми (1’—4′) клапанами:1,1′,3, 3’— «карман» закрыт;2, 2′, 4, 4′ — «карман» открыт

где 12,5 кВт — потери мощности на трение в одном компрессорном цилиндре; n_ц — число цилиндров поршневого компрессора.

1. Уравнение неразрывности для установившегося движения газа.

2. Формула массового расхода для установившегося движения газа.

3. Практические формулы для гидравлического расчета газопроводов.

4. Влияние рельефа трассы на пропускную способность газопровода.

5. Влияние неизотермичности потока на пропускную способность газопровода.

6. Изменение давления по длине газопровода. Среднее давление.

7. Расчеты сложных газопроводов: по эквивалентному диаметру, по эквивалентному расходу, по коэффициентам расхода. Примеры.

8. Эффективность перемычек на параллельных газопроводных системах.

9. Возможные варианты увеличения пропускной способности газопроводов.

10. Увеличение пропускной способности прет сооружении многониточных газопроводных систем.

11. Определение длины последнего перегона газопровода.

12. Расчет режимов работы КС с центробежными нагнетателями.

13. Загрузочные кривые для поршневых компрессорных машин.

Лекция№13

§ 47. Расчет сложных газопроводов

Любую сложную газопроводную систему можно разбить на элементы, к каждому из которых можно применить расчетные зависимости для простых газопроводов при выполнении в узловых точках следующих условий: равенство давлений и сохранения массы газа (уравнение неразрывности). Такой поэтапный способ расчета является трудоемким. Во многих случаях процедура расчета упрощается посредством приведения сложной системы к фиктивному простому газопроводу.

При этом оперируют такими понятиями, как эквивалентный газопровод, эквивалентный расход и коэффициент расхода.

Простой газопровод будет эквивалентен сложной газопроводной системе, если у него и у системы будут одинаковы все параметры перекачки (расходы и давление в начале и конце, температура, теплофизические характеристики перекачиваемого газа), т.е. при различии в геометрических размерах потери на трение в эквивалентном газопроводе будут такими же, что и в сложной системе. Эквивалентными между собой могут быть и два простых газопровода, отличающихся только диаметром и длиной.

Эквивалентным расходом пользуются для расчета газопроводов с переменным расходом по длине. Эквивалентный расход — это такой усредненный и постоянный по длине расход, при котором будут такие же потери на трение, что и при изменяющемся расходе по длине. В данном случае опять сложная газопроводная система заменяется простым эквивалентным газопроводом, но в отличие от предыдущего случая геометрические размеры газопровода остаются теми же самыми. Таким образом, при применении эквивалентного расхода соблюдается равенство всех параметров за исключением расходов.

Коэффициент расхода — это отношение расходов проектируемого газопровода к расходу эталонного простого газопровода. С помощью коэффициента расхода любую газопроводную сложную систему (или простой газопровод) можно привести по пропускной способности к одному эталонному газопроводу и этим самым упростить расчет.

Рассмотрим наиболее часто встречающиеся случаи.

Однониточные газопроводы с участками различного диаметра.

Пусть имеем сложный газопровод с участками разных диаметров. Необходимо определить размеры эквивалентного ему газопровода при одних и тех же параметрах перекачки. Можно воспользоваться формулой расхода в любом виде. Из уравнения расхода запишем разность квадратов давлений для первого участка длиной R₁ [например, на основании формулы (9.11)]

где

Аналогично запишем разность квадратов давлений для второго, третьего и n-го участков

Просуммировав соответственно левые и правые части уравнений системы, получим

(9.37) 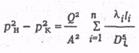155

Лекция№14 Увеличение пропускной способности газопровода. Увеличение числа

Последнее изменение этой страницы: 2017-05-11; Просмотров: 996; Нарушение авторского права страницы

Кратко о гидродинамике: уравнения движения

Написав предыдущий пост, исторический и отчасти рекламный (хотя потенциальные абитуриенты такое вряд ли читают), можно перейти и к разговору «по существу». К сожалению, высокой степени популярности описания добиться вряд ли получится, но всё же постараюсь не устраивать курс сухих лекций. Хотя, от сухости избавиться не удалось, да и пост писался в результате ровно месяц.

В нынешней публикации описаны основные уравнения движения идеальной и вязкой жидкости. По возможности кратко рассмотрен их вывод и физический смысл, а также описаны несколько простейших примеров их точных решений. Увы, этими несколькими примерами доступные аналитически решения уравнений Навье-Стокса в значительной мере исчерпываются. Напомню, что Институт Клэя отнёс доказательство существования и гладкости решений к проблемам тысячелетия. Гении уровня Перельмана и выше — задача вас ждёт.

Понятие сплошной среды

В, если можно так выразиться, «традиционной» гидродинамике, сложившейся исторически, фундаментом является модель сплошной среды. Она отвлекается от молекулярной структуры вещества, и описывает среду несколькими непрерывными полевыми величинами: плотностью, скоростью (определяемой через суммарный импульс молекул в заданном элементе объёма) и давлением. Модель сплошной среды предполагает, что в любом бесконечно малом объёме содержится ещё достаточно много частиц (как принято говорить, термодинамически много — числа, близкие по порядку величины к числу Авогадро — 10 23 шт.). Таким образом, модель ограничена снизу дискретностью молекулярной структуры жидкости, что в задачах типичных пространственных масштабов совершенно несущественно.

Однако, такой подход позволяет описать не только воду в пробирке или водоёме, и оказывается куда более универсальным. Поскольку наша Вселенная на больших масштабах практически однородна, то, как ни странно, она начиная с некоторого масштаба превосходно описывается как сплошная среда, с учётом, конечно же, самогравитации.

Другими, более приземлёнными применениями сплошной среды являются описание свойств упругих тел, динамики плазмы, сыпучих тел. Также можно описывать топлу людей как сжимаемую жидкость.

Параллельно с приближением сплошной среды, в последние годы набирает обороты кинетическая модель, основанная на дискретизации среды на небольшие частицы, взаимодействующие между собой (в простейшем случае — как твердые шарики, отталкивающиеся при столкновении). Такой подход возник в первую очередь благодаря развитию вычислительной техники, однако существенно новых результатов в чистую гидродинамику не превнёс, хотя оказался крайне полезен для задач физики плазмы, которая на микроуровне не является однородной, а содержит электроны и положительно заряженные ионы. Ну и опять же для моделирования Вселенной.

Уравнение неразрывности. Закон сохранения массы

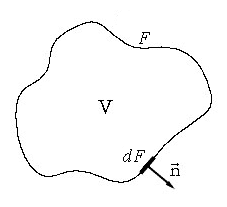
Самый элементарный закон. Пусть у нас есть какой-то совершенно произвольный, но макроскопический объём жидкости V, ограниченный поверхностью F (см. рис.). Масса жидкости внутри него определяется интегралом:

И пусть с жидкостью внутри него не происходит ничего, кроме движения. То есть, там нет химических реакций и фазовых переходов, нет трубок с насосами или чёрных дыр. Ну и всё происходит с маленькими скоростями и для малых масс вещества, потому никакой теории относительности, искривления пространства, самогравитации жидкости (она становится существенна на звёздных масштабах). И пусть сам объём и границы еего неподвижны. Тогда единственное, что может изменить массу жидкости в нашем объёме — это её перетекание через границу объёма (для определённости — пусть масса в объёме убывает):

где вектор j — поток вещества через границу. Точкой, напомним, обозначается скалярное произведение. Поскольку границы объёма, как было сказано, неподвижны, то производную по времени можно внести под интеграл. А правую часть можно преобразовать к такому же, как слева, интегралу по объёму по теореме Гаусса-Остроградского.

В итоге, в обеих частях равенства получается интеграл по одному и тому же совершенно произвольному объёму, что позволяет приравнять подинтегральные выражения и перейти к дифференциальной форме уравнения:

Здесь (и далее) использован векторный оператор Гамильтона. Образно говоря, это условный вектор, компоненты которого — операторы дифференцирования по соответствующим координатам. С его помощью можно очень кратко обозначать разного рода операции над скалярами, векторами, тензорами высших рангов и прочей математической нечистью, основные среди которых — градиент, дивергенция и ротор. Не буду останавливаться на них детально, поскольку это отвлекает от основной темы.

Наконец, поток вещества равен массе, переносимой через единичную площадку за единицу времени:

Окончательно, закон сохранения массы (называемый также уравнением неразрывности) для сплошной среды таков:

Это выражение наиболее общее, для среды, обладающей переменной плотностью. В реальности, эксперимент свидетельствует о крайне слабой сжимаемости жидкости и практически постоянном значении плотности, что с высокой точностью позволяет применять закон сохранения массы в виде условия несжимаемости:

которое с не менее хорошей точностью работает и для газов, пока скорость течения мала по сравнению со звуковой.

Уравнение Эйлера. Закон сохранения импульса

Весь относительно громоздкий процесс колдовства преобразования интегралов, использованный выше, даёт нам не только уравнение неразрывности. Точно такие же по сути преобразования позволяют выразить законы сохранения импульса и энергии, и получить в итоге уравнения для скорости жидкости и для переноса тепла в ней. Однако пока не будем сильно торопиться, и займёмся не просто сохранением импульса, а даже сохранением импульса в идеальной несжимаемой жидкости — т.е. рассмотрим модель с полным отсутствием вязкости.

Рассуждения практически те же самые, только теперь нас интересует не масса, а полный импульс жидкости в том же самом объёме V. Он равен:

При тех же самых условиях, что и выше, импульс в объёме может меняться за счёт:

• конвективного переноса — т.е. импульс «утекает» вместе со скоростью через границу
• давления окружающих элементов жидкости
• просто за счёт внешних сил, например — от силы тяжести.

Соответствующие интегралы (порядок отвечает списку) дают такое соотношение:

Начнём их преобразовывать. Правда, для этого нужно воспользоваться тензорным анализом и правилами работы с индексами. Конкретнее, к первому и второму интегралам применяется теорема Гаусса-Остроградского в обобщённой форме (она работает не только для векторных полей). И если перейти к дифференциальной форме уравнения, то получится следующее:

Крестик в кружочке обозначает тензорное произведение, в данном случае — векторов.

В принципе, это уже уравнение Эйлера, однако его можно чуток упростить — ведь закон сохранения массы никто не отменял. Раскрыв здесь скобки в дифференциальных операторах и приведя затем подобные слагаемые, мы увидим, что три слагаемых благополучно собираются в уравнение неразрывности, и потому дают в сумме ноль. Итоговое уравнение оказывается таким:

Если перейти в систему отсчёта, связанную с движущейся жидкостью (не будем заострять внимание на том, как это делается), мы увидим, что уравнение Эйлера выражает второй закон Ньютона для единицы объёма среды.

Учёт вязкости. Уравнение Навье-Стокса

Идеальная жидкость, это, конечно, хорошо (правда, всё равно точно не решается), но во многих случаях учёт вязкости необходим. Даже в той же конвекции, в течении жидкости по трубам. Без вязкости вода вытекала бы из наших кранов с космическими скоростями, а малейшая неоднородность температуры в воде приводила бы к её крайне быстрому и бурному перемешиванию. Потому давайте учтём сопротивление жидкости самой себе.

Дополнить уравнение Эйлера можно различными (но эквивалентными, конечно же) путями. Воспользуемся базовой техникой тензорного анализа — индексной формой записи уравнения. И пока также отбросим внешние силы, чтобы не путались под руками / под ногами / перед глазами (нужное подчеркнуть). При таком раскладе всё, кроме производной по времени, можно собрать в виде дивергенции одного такого тензора:

По смыслу, это плотность потока импульса в жидкости. К нему и нужно добавить вязкие силы в виде ещё одного тензорного слагаемого. Поскольку они явно приводят к потере энергии (и импульса), то они должны вычитаться:

Идя обратно в уравнение с таким тензором, мы получим обобщённое уравнение движения вязкой жидкости:

Оно допускает любой закон для вязкости.

Принято считать очевидным, что сопротивление зависит от скорости движения. Вязкость же, как перенос импульса между участками жидкости с различными скоростями, зависит от градиента скорости (но не от самой скорости — тому мешает принцип относительности). Если ограничиться разложением этой зависимости до линейных слагаемых, получится вот такой жутковатый объект:

в котором величина перед производной содержит 81 коэффициент. Однако, используя ряд совершенно разумных предположений об однородности и изотропности жидкости, от 81 коэффициента можно перейти всего к двум, и в общем случае для сжимаемой среды, тензор вязких напряжений равен:

где η (эта) — сдвиговая вязкость, а ζ (зета или дзета) — объёмная вязкость. Если же среда ещё и несжимаема, то достаточно одного коэффициента сдвиговой вязкости, т.к. второе слагаемое при этом уходит. Такой закон вязкости

носит название закона Навье, а полученное при его подстановке уравнение движения — это уравнение Навье-Стокса:

Точные решения

Главной проблемой гидродинамики является отсутствие точных решений её уравнений. Как бы с этим ни боролись, но получить действительно всеобщих результатов не удаётся до сих пор, и, напомню, вопрос существования и гладкости решений уравнений Навье-Стокса входит в список Проблем тысячелетия института Клэя.

Однако, несмотря на столь грустные факты, некоторые результаты есть. Здесь будут представлены далеко не все, а лишь самые простые случаи.

Потенциальные течения

Особый интерес представляют течения, в которых жидкость не завихряется. Для такой ситуации можно отказаться от рассмотрения векторного поля скорости, поскольку она выражается через градиент скалярной функции — потенциала. Потенциал же удовлетворяет хорошо изученному уравнению Лапласа, решение которого полностью определяется тем, что задано на границах рассматриваемой области:

Более того, при отсутствии вязкости из уравнения Эйлера можно однозначно выразить и давление, что вовсе замечательно и приводит нас к полному решению задачи. Ах, если бы так было всегда… то гидродинамики, наверное, уже бы и не было как современной и актуальной отрасли.

Дополнительно можно упростить задачу предположением, что течение жидкости двумерно — скажем, всё движется в плоскости (x,y), и ни одна частица не перемещается вдоль оси z. Можно показать, что в таком случае скорость может быть также заменена скалярной функцией (на этот раз — функцией тока):

которая при потенциальном течении удовлетворяет условиям Коши-Лагранжа из теории функций комплексной переменной и воспользоваться соответствующим математическим аппаратом. Полностью совпадающим с аппаратом электростатики. Теория потенциальных течений развита на высоком уровне, и в принципе хорошо описывает большой спектр задач.

Простые течения вязкой жидкости

Решения для вязкой жидкости чаще всего удаётся получить, когда из уравнения Навье-Стокса благодаря свойствам симметрии задачи выпадает нелинейное слагаемое.

Сдвиговое течение Куэтта

Самая элементарная задачка. Канал с неподвижной нижней и подвижной верхней стенкой, которая движется равномерно с некоторой скоростью. На границах жидкость прилипает к ним, так что скорость жидкости равна скорости границы. Этот результат является экспериментальным фактом, и как-то даже авторы первых экспериментов не упоминаются, просто — по совокупности экспериментов.

В такой ситуации от уравнения Навье-Стокса останется уравнение вида v» = 0, и потому профиль скорости в канале окажется линейным:

Данная задача является практически базовой для теории смазки, т.к. позволяет непосредственно определить силу, которую требуется приложить к верхней стенке для её движения с конкретной скоростью.

Течение Пуазейля

Вторая по элементарности — ламинарное течение в канале. Или в трубе. Результат оказывается один — профиль скорости является параболическим:

На основе решения Пуазейля можно определить расход жидкости через сечение канала, но, правда, только при ламинарном течении и гладких стенках. С другой стороны, для турбулентного потока и шероховатых стенок точных решений нет, а есть лишь приближённые эмпирические закономерности.

Стекание слоя жидкости по наклонной плоскости

Тут — почти как в задаче Пуазейля, только верхняя граница жидкости будет свободной. Если предположить, что по ней не бегут никакие волны, и вообще сверху нет трения, то профиль скорости будет практически нижней половинкой предыдущего рисунка. Правда, если из полученной зависимости вычислить скорость течения для средней равнинной речки, она составит около 10 км/с, и вода должна самопроизвольно отправляться в космос. Наблюдаемые в природе низкие скорости течения связаны с развитой завихренностью и турбулентностью потока, которые эффективно увеличивают вязкость воды примерно в 1 млн. раз.

В следующем посте планируется рассказать о законе сохранения энергии и соответствующих ему уравнениях переноса тепла при течении жидкости.

Тема 3. Кинематика и динамика жидкостей и газов, Лекция 11. Уравнение Бернулли и следствия из него

Тема 3. Кинематика и динамика жидкостей и газов

Лекция 11. Уравнение Бернулли и следствия из него

1. Основные положения гидродинамики. Уравнение неразрывности струи.

2. Уравнение Бернулли.

3. Истечение жидкости из отверстия. Принцип реактивного движения.

ОТВОДИМОЕ ВРЕМЯ: 2 часа.

1. Суханов курс физики. — М.: 1996.

2. Савельев общей физики. Том 1. — M: — Наука, 1996. § 72,73,74.

3. Трофимова физики. – М.: Высшая школа, 1999. § 28,29,30.

4. , Детлаф по физике. — М.: Наука, 1996. Отдел III.

Современные летательные аппараты способны выполнять саше разнообразные задачи и осуществлять полет в различных физических условиях. Физическими условиями полета называется совокупность фи­зических свойств атмосферы и физических явлений, возникающих во время полета летательных аппаратов. Физические условия полета оп­ределяются, в первую очередь, назначением летательного аппарата и могут значительно, а порой и быстро, изменяться в процессе полета. Ярким примером являются пилотируемые космические корабли многора­зового использования, способные осуществлять полет как в околозем­ном космическом пространстве, т. е. в практически безвоздушном пространстве, так и в нижних плотных слоях атмосферы.

В безвоздушном пространстве полет летательных аппаратов осно­ван на реактивном принципе движения, т. е. на законах движения тел с переменной массой, вытекающих из основных законов динамики поступательного движения твердых тел.

Полет летательных аппаратов в воздушной среде подчиняется за­конам аэродинамики, начало которой положено трудами русского уче­ного () и его ученика . В основе аэродинамики, как науки, лежит гидродинамика — физическая теория движения несжимаемых жидкостей с твердыми телами.

Основные положения и выводы гидродинамики применимы не только к жидкостям, но и к газам в том случае, когда сжимаемостью их мож­но пренебречь. Соответствующие расчеты показывают, что при движе­нии жидкостей и газов со скоростями меньшими скорости звука, их с достаточной степенью точности можно считать несжимаемыми. Следова­тельно, движение твердых тел, в том числе летательных аппаратов, в воздушной среде при указанных Скоростях подчиняется законам гидро­динамики.

Для выяснения физической сущности процессов, определяющих по­лет летательных аппаратов, необходимо уяснить основные положения гидродинамики.

1. ОСНОВНЫЕ ПОЛОЖЕНИЯ ГИДРОДИНАМИКИ. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ СТРУИ

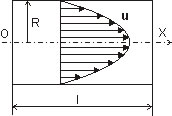
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости потоком. Графически движение жидкостей изображается с помощью линий, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 1).

Линии тока проводятся так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т. е. можно определить состояние движения жидкости. Линии тока в жидкости можно «проявить», например, подмешав в нее какие-либо заметные взвешенные частицы.

Часть жидкости, ограниченную линиями тока, называют трубкой тока.

Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.

Рассмотрим какую-либо трубку тока. Выберем два ее сечения S1 и S2, перпендикулярные направлению скорости (рис. 2).

За время Δt через сечение S проходит объем жидкости SvΔt; следовательно, за 1с через S1 пройдет объем жидкости S1v1, где v1 — скорость течения жидкости в месте сечения S1. Через сечение S2 за 1с пройдет объем жидкости S2v2, где v2 — скорость жидкости в месте сечения S2. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (ρ=const), то через сечение S2 пройдет такой же объем жидкости, как и через сечение S1, т. е.

Следовательно, произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение 1 называется уравнением неразрывности для несжимаемой жидкости.

2. УРАВНЕНИЕ БЕРНУЛЛИ

Выделим в стационарно текущей идеальной жидкости (физическая абстракция, т. е. воображаемая жидкость, в которой отсутствуют силы внутреннего трения) трубку тока, ограниченную сечениями S1 и S2, по которой слева направо течет жидкость (рис. 3).

Пусть в месте сечения S1 скорость течения v1 давление Р1 и высота, на которой это сечение расположено, h1. Аналогично, в месте сечения S2 скорость течения v2, давление Р2 и высота сечения h2. За малый промежуток времени Δt жидкость перемещается от сечения S1 к сечению S’1, от S2 к S’2.

Согласно закону сохранения энергии, изменение полной энергии E2-E1 идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы жидкости:

где E1 и Е2 — полные энергии жидкости массой m в местах сечений S1 и S2 соответственно.

С другой стороны, А — это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S1 и S2, за рассматриваемый малый промежуток времени Δt. Для перенесения массы m от S1 до S’1 жидкость должна переместиться на расстояние l1 =v1 Δt и от S2 до S’2 — на расстояние l2 =v2 Δt. Отметим, что 11 и 12 настолько малы, что всем точкам объемов, закрашенных на рис. 3, приписывают постоянные значения скорости v, давления Р и высоты h. Следовательно,

где F1=P1S1 и F2=-P2S2 (отрицательна, так как направлена в сторону, противоположную течению жидкости; рис. 3).

Полные энергии Е1 и Е2 будут складываться из кинетической и потенциальной энергий массы m жидкости:

(4)

(5)

Подставляя (4) и (5) в (2) и приравнивая (2) и (3), получим

(6)

Согласно уравнению неразрывности струи для несжимаемой жидкости (1), объем, занимаемый жидкостью, остается постоянным, т. е.

Разделив выражение (6) на , получим

,

где ρ — плотность жидкости. Но так как сечения выбирались произвольно, то можем записать

=const. (7)

Выражение (7) выведено швейцарским физиком Д. Бернулли (1700—1782; опубликовано в 1738 г.) и называется уравнением Бернулли. Как видно из его вывода, уравнение Бернулли — выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Оно хорошо выполняется и для реальныхжидкостей, внутреннее трение которых не очень велико.

Величина Р в формуле (7) называется статическим давлением (давление жидкости поверхность обтекаемого ею тела), величина — динамическим давлением. Величина представляет собой гидростатическое давление.

Для горизонтальной трубки тока (h1=h2) выражение (7) принимает вид

=const, (8)

— называется полным давлением.

Из уравнения Бернулли (8) для горизонтальной трубки тока и уравнения неразрывности (1) следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно продемонстрировать, установив вдоль трубы ряд манометров (рис. 4).

В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.

Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито — Прандтля (рис. 5).

Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоединены к манометру. I помощью одной из трубок измеряется полное давление (Р0), с помощью другой — статическое (Р). Манометром измеряют разность давлений:

, (9)

где — плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:

(10)

Из формул (9) и (10) получаем искомую скорость потока жидкости:

Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса (рис. 6).

Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавливается и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом, можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст.= 133,32 Па).

Уравнение Бернулли позволяет описать физические явления лежащие в основе работы целого ряда устройств и приборов: карбюратор, пульверизатор (рис. 7) и др.

3. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЯ. ПРИНЦИП РЕАКТИВНОГО ДВИЖЕНИЯ

Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие (рис. 8).

Рассмотрим два сечения (на уровне h1 свободной поверхности жидкости в сосуде и на уровне h2 выхода ее из отверстия) и напишем уравнение Бернулли:

Так как давления Р1 и Р2 в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. Р1=Р2 , то уравнение будет иметь вид

.

Из уравнения неразрывности (1) следует, что v1/v2 = S1/S2, где S1 и S2 — площади поперечных сечений сосуда и отверстия. Если S1>>S2, то членом можно пренебречь и

(11)

Это выражение получило название формулы Торричелли (Э. Торричелли (1608 – 1647) – итальянский физик и математик.

Итак, скорость истечения жидкости из отверстия, расположенного на глубине h под открытой поверхностью, совпадает со скоростью, которую приобретает любое тело, падая с высоты h. Следует помнить, что этот результат получен в предположении, что жидкость идеальна. Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличается от значения (11), чем больше вязкость жидкости.

Струя жидкости, вытекающая из отверстия в сосуде (рис. 9), уносит с собой за время Δt импульс (— плотность жидкости, S — площадь отверстия, v — скорость истечения струи).

Этот импульс сообщается вытекающей жидкости сосудом. По третьему закону Ньютона сосуд получает, от вытекающей жидкости за время Δt импульс, равный — , т. е. испытывает действие силы

(12)

Эта сила называется реакцией вытекающей струи. Если сосуд поставить на тележку, то под действием силы Fr он придет в движение в направлении, противоположном направлению струи.

Найдем значение силы Fr, воспользовавшись выражением (11) для скорости истечения жидкости из отверстия:

(13)

Если бы, как это может показаться на первый взгляд, сила Fr совпадала по величине с силой гидростатического давления, которое жидкость оказывала бы на пробку, закрывающую отверстие, то Fr была бы равна . На самом деле сила Fr оказывается в 2 раза большей. Это объясняется тем, что возникающее при вытекании струи движение жидкости в сосуде приводит к перераспределению давления, причем давление вблизи стенки, лежащей против отверстия, оказывается несколько большим, чем вблизи стенки, в которой сделано отверстие.

На реакции вытекающей струи газа основано действие реактивных двигателей и ракет. Реактивное движение, не нуждаясь для своего осуществления в наличии атмосферы, используется для полетов в космическом пространстве.

Основоположником теории межпланетных сообщений является выдающийся русский ученый и изобретатель (1857—1935). Он дал теорию полета ракеты и обосновал возможность применения реактивных аппаратов для межпланетных сообщений. В частности, Циолковским была разработана теория движения составных ракет, в которых каждая последующая ступень вступает в действие после того, как предыдущая ступень, израсходовав полностью топливо, отделится от ракеты. Идеи Циолковского получили дальнейшее развитие и были осуществлены учеными и инженерами для освоения космического пространства.