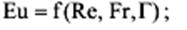Уравнение неразрывности сплошности фильтрационного потока

Уравнение неразрывности (сплошности)

Фильтрационного потока

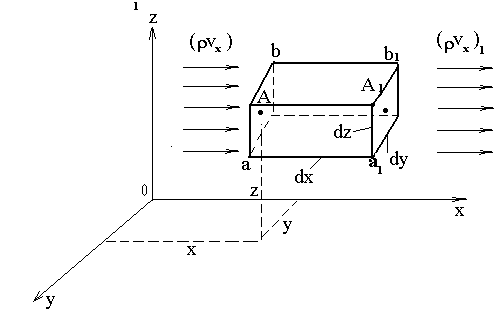
Выведем уравнение неразрывности (сплошности) фильтрационного потока сжимаемого флюида в деформируемой пористой среде (самый общий случай). Для этого выделим в пористой среде элементарный объем в виде параллелепипеда с ребрами dx, dy, dz (рис. 5), причем длины ребер во много раз больше поперечных размеров поровых каналов.

Рис.5

В рассматриваемом общем случае неустановившегося движения сжимаемой жидкости (флюида) скорость фильтрации `V и плотность жидкости r являются функциями координат и времени, т.е.

Проекции на ось X массовых скоростей фильтрации в точках А и А_1, расположенных в центрах боковых граней ab и a₁b₁, соответственно равны

rV_x, и (rV_x)₁ = rV_x + .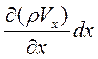

Заметим, что в силу малости выделенного объема и его граней можно считать, что плотность r и скорость фильтрации `V распределены на гранях ab и a₁b₁ равномерно и равны значениям их в точках А и А₁ соответственно.

Масса флюида, поступающего в выделенный элемент через левую грань ab за малый промежуток времени dt, равна rV_x*dydzdt.

Масса флюида, вытекающего из выделенного объема через правую грань a₁b₁ за этот же отрезок времени dt, равна

.

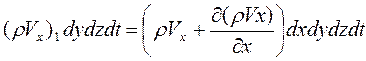
Тогда изменение массы флюида в объеме выделенного элемента aba₁b₁ за отрезок времени dt за счет потока вдоль оси Х будет равна:

dM_x = [ (rV_x)₁ — (rV_x) ] dydzdt = 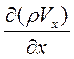dxdydzdt.

Рассматривая фильтрацию флюида в направлении осей Y и Z, получим аналогичные выражения для изменения массы в элементарном объеме за счет потока вдоль этих осей в виде:

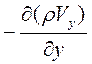
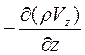
dM_y = dxdydzdt, dM_z = dxdydzdt .

Тогда общее изменение (накопление) массы флюида в объеме выделенного элемента aba₁b₁ за время dt будет равно:

т.е. dM = — 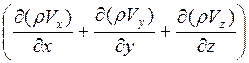* dxdydzdt . (2.9)

С другой стороны, масса флюида, находящегося в рассматриваемом поровом объеме элемента aba₁b₁, равна

где m — коэф. пористости пласта.

Изменение массы флюида в этом же элементарном объеме aba₁b₁ за время dt можно записать так (объем элемента dxdydz фиксирован)

dM = 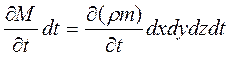. (2.10)

Приравнивая выражения (2.9) и (2.10) и сокращая их на dxdydzdt, получаем уравнение неразрывности фильтрационного потока.

. (2.11)

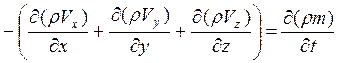
С физической точки зрения уравнение неразрывности (2.11) представляет собой уравнение материального баланса фильтрующейся жидкости (флюида) и выражает закон сохранения массы.

Заметим дополнительно, что уравнение неразрывности (2.11) справедливо только в том случае, когда внутри выделенного элемента пласта нет источников или стоков; это означает, что жидкость или газ движутся в продуктивном пласте без разрывов в сплошности потока, и что в поле скоростей фильтрации нет особых точек (например, скважин), в которых жидкость (газ) может «исчезать» или «появляться». При движении жидкостей (газов) в пласте к скважинам это уравнение (2.11) справедливо во всех точках пласта вне скважины.

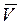
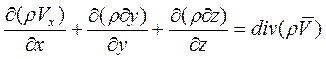
Выражение в левой части уравнения (2.11) представляет собой дивергенцию вектора массовой скорости r и кратко записывается так:

.

Поэтому уравнение неразрывности (2.11) принимает краткую запись

. (2.12)

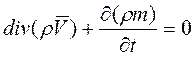
Для круглого трубопровода и несжимаемой жидкости объемный расход

рассчитывается по уравнению:

Сплошной (неразрывный) поток жидкости – поток, в котором отсутствуют пустоты, движение происходит с непрерывным распространением массы; масса жидкости, проходящая через любое сечение, согласно закону сохранения массы, есть величина постоянная.

Уравнение неразрывности (сплошности) потока в дифференциальной форме:

– дифференциальное уравнение неразрывности потока для неустановившегося движения сжимаемой жидкости;

– дифференциальное уравнение неразрывности потока для установившегося движения сжимаемой жидкости;

=

– дифференциальное уравнение неразрывности потока для установившегося движения несжимаемой жидкости,

– изменение скоростей вдоль осей координат x,y,z.

Уравнение неразрывности потока в интегральной форме – уравнение постоянства расхода:

Скорости капельной жидкости в различных поперечных сечениях трубопровода обратно пропорциональны площадям этих сечений:

.

Гидравлический радиус– отношение площади S сечения потока к смоченному периметру П, характеризует каналы некруглого сечения:

Эквивалентный диаметр – геометрическая характеристика канала некруглого сечения, равен отношению учетверенной площади живого сечения, через которое протекает жидкость, к смоченному периметру:

Движение жидкости – перемещение жидкости по трубопроводам, аппаратам, каналам и т.д. Различают установившееся и неустановившееся, свободное и вынужденное, напорное и безнапорное движения. При установившемся движении поля давлений и скоростей не изменяются во времени, а при неустановившемся – изменяются. Свободное движение возникает за счет разности плотностей в различных точках объема жидкости. Вынужденное движение создается внешними силами, создаваемыми насосами, мешалками, центрифугами и др. При напорном течении жидкость заполняет все сечение трубопровода, при безнапорном – только часть сечения заполнена жидкостью, имеется свободная поверхность. Различают ламинарный и турбулентный режимы движения жидкостей.

Критерий Рейнольдса — единый безразмерный комплекс, по численному значению которого можно судить о режимах течения жидкости, является мерой соотношения между силами инерции и силами вязкости. Переход от ламинарного режима к турбулентному осуществляется тем легче, чем больше массовая скорость жидкости ρw, чем больше диаметр трубы и чем меньше вязкость жидкости:

Ламинарный режим движения– все частицы жидкости перемещаются равномерно по параллельным траекториям. Наблюдается при значениях критерия Рейнольдса меньше критического Re_кр (Re Re_кр =2320) в прямых и гладких трубах постоянного сечения. В интервале значений 2320 2 /g2 напоров (высот) есть величина постоянная, равная суммарному (полному) гидродинамическому напору; данное уравнение выражает закон сохранения энергии – для движущейся среды любого сечения потока при установившемся движении идеальной жидкости сумма удельной (отнесенной к 1Н жидкости) потенциальной

энергий есть величина постоянная:

или для двух поперечных сечений потока

Дифференциальные уравнения движения реальной жидкости Навье – Стокса – выражают связь между массовыми, поверхностными, инерционными и вязкостными силами в потоке, характеризуют закон сохранения энергии при движении вязкой жидкости:

где ∇ 2 w_x, ∇ 2 w_y ∇ 2 w_z – операторы Лапласа, представляют собой суммы вторых производных по осям координат. Согласно второй теореме подобия решение уравнений Навье – Стокса можно представить в виде обобщенного критериального уравнения гидродинамики:

для установившегося движения реальной жидкости

где Eu – критерий Эйлера, определяемый критерий; Re, Fr, Ho — критерии Рейнольдса, Фруда, гомохронности, являются определяющими критериями; Г – симплекс геометрического подобия.

В виде степенной зависимости критериальное уравнение принимает вид:

где A, m, n, p, q – постоянные, определяемые опытным путем для группы подобных явлений.

Основные критерии гидродинамического подобия представлены в табл. 2.

1. Какие процессы называются тепловыми?

2. Дайте определение движущей силы тепловых процессов.

3. Сформулируйте определения температурного поля, изотермической поверхности и температурного градиента.

4. Какими способами осуществляется перенос тепла в теплообменных процессах?

5. Запишите закон теплопроводности Фурье. Сформулируйте физический смысл и укажите размерность коэффициента теплопроводности.

6. В каких единицах измеряется коэффициент температуропроводности?

7. Запишите уравнения теплопроводности плоской и цилиндрической стенок.

8. Сформулируйте законы теплового излучения.

9. Что называется процессом теплоотдачи? От каких факторов зависит коэффициент теплоотдачи, в каких единицах измеряется?

10. Назовите основные критерии теплового подобия и сформулируйте их физический смысл.

11. Каким образом определяется коэффициент теплоотдачи в случае пленочной конденсации?

12. Что такое теплопередача? Укажите физический смысл, размерность коэффициента теплопередачи.

13. Каким образом определяется средняя движущая сила процесса теплопередачи при различных взаимных направлениях теплоносителей?

14. Что является целью расчета теплообменного аппарата?

15. Дайте классификацию теплообменных аппаратов.

16. Назовите основные греющие агенты в зависимости от температуры нагреваемой среды.

17. Каким образом осуществляется умеренное и глубокое охлаждение?

18. Какие типы конденсаторов различают по способу охлаждения?

19. Что такое выпаривание?

20. Дайте классификацию выпарных установок.

21. Перечислите основные типы выпарных аппаратов.

22. Запишите тепловой и материальный балансы однокорпусного выпаривания.

23. Сформулируйте понятия первичного и вторичного паров.

24. Что такое температурные потери и полезная разность температур?

25. Каким образом рассчитывается температура кипения раствора?

Гидравлические элементы потока, расход, средняя скорость. Уравнение неразрывности (сплошности) потока.

В качестве основных элементов, характеризующих поток жидкости, различают: площадь живого сечения, смоченный периметр, гидравлический радиус, эквивалентный диаметр, средняя скорость потока, расход жидкости.

Живым сечением называется сечение потока, проведенное перпендикулярно линиям тока. (Линией тока называется такая линия, касательные к которой в любой точке, совпадают с направлением векторов скорости частиц в данный момент времени.)

Смоченный периметр – часть периметра живого сечения потока, в которой жидкость соприкасается с твердыми стенками канала или трубы. (χ, м).

Гидравлический радиус – характеристика живого сечения, представляющая собой отношение площади живого сечения к смоченному периметру

R=w/ χ

Средняя скорость – фиктивная скорость (v, м/с), с которой должны двигаться все частицы жидкости в данном живом сечении, чтобы расход, проходящий через него, был равен расходу, вычисленному по действительным скоростям всех частиц в этом же сечении. v=Q/w

Расход– количество жидкости, протекающей через живое сечение потока в единицу времени.

расход жидкости по тока равен произведению площади его живого сечения на среднюю скорость(Q=v * w). При движении жидкости различают, соответственно расходы: объемный, весовой и массовый.

u1 w1=u2 w2=……=un wn=const

Это уравнение называется уравнением неразрывности (сплошности) для элементарной

струйки. Оно показывает, что при установившемся движении элементарный объемный расход несжимаемой жидкости есть величина постоянная вдоль всей струйки.

Учитывая, что поток жидкости представляет собой совокупность большого числа элементарных струек, сплошь заполняющих площадь его живого cечения, общий расход жидкости для всего потока, очевидно, можно определить как сумму

элементарных расходов отдельных струек, из которых состоит

u – скорость элементарных струек

Уравнение Д. Бернулли для элементарной струйки невязкой жидкости.

Это и есть уравнение Д. Бернулли для элементарной струйки идеальной жидкости. Оно показывает, что для элементарной струйки идеальной жидкости полная удельная энергия, т .е . сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии,есть величина постоянная во всех сечениях.

Члены уравнения Бернулли измеряются в единицах длины и носят следующие название: z — нивелирная высота, или геометрический напор; р/γ — пьезометрическая высота; u 2 /2g —

скоростная высота, или скоростной напор.

Уравнение Д. Бернулли для элементарной струйки реальной жидкости. Геометрическое и энергетическое толкование уравнения Д. Бернулли.

Благодаря вязкости в реальной жидкости происходят потери механической энергии потока на трение внутри жидкости и о стенки канала. При этом происходит рассеивание (диссипация) энергии. Энергия, потерянная на трение, превращается в теплоту и идет на пополнение запаса внутренней энергии жидкости, а часть ее отводится в виде тепла через стенки канала.

Внутренняя энергия жидкости не может быть непосредственно использована для приведения жидкости в движение и поэтому в гидравлике рассматривается как потеря механической энергии (потеря напора).

Для реальной жидкости равенство нарушается, и вместо него имеем , где – потеря напора на участке 1–2. Тогда для элементарной струйки реальной жидкости уравнение Бернулли примет вид

Таким образом, полный напор вдоль струйки реальной жидкости уменьшается. Для характеристики относительного изменения полного напора на единицу длины вводится понятие о гидравлическом уклоне

Например, на участке трубопровода 1–2 (см. рис. 4.26)

где l1-2 – длина участка 1–2.

Таким образом, гидравлическим уклоном называется отношение потери напора к длине, на которой она происходит.

Кроме того, вводится еще понятие о пьезометрическом уклоне

Пьезометрический уклон может быть положительным, равным нулю и отрицательным.