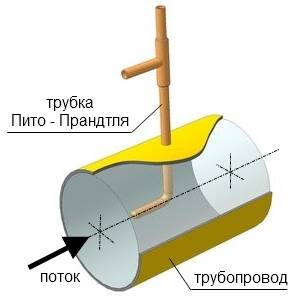
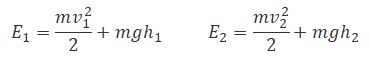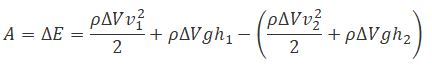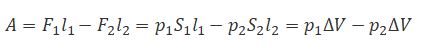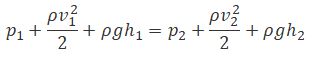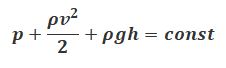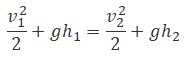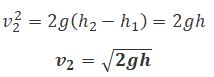Уравнение неразрывности трубки тока жидкости

Уравнение неразрывности трубки тока жидкости

Гидродинамика представляет собой раздел механики сплошных сред, в котором изучается движение несжимаемых жидкостей и взаимодействие несжимаемых жидкостей с твердыми телами.

1.6.1. Линии и трубки тока. Неразрывность струи

Состояние движения жидкости можно определить, указав для каждой точки пространства вектор скорости как функцию времени. Совокупность векторов , заданных для всех точек пространства, образует поле векторов скорости. Проведем в движущейся жидкости линии так, чтобы касательная к ним в каждой точке совпадала по направлению с вектором (Рис. 1.6.1). Эти линии называются линиями тока .

Рис. 1.6.1. Линии тока в жидкости

Густота линий (отношение числа линий к единичной площадке) пропорциональна величине скорости в данном месте.

Картина линий тока может непрерывно меняться. Если вектор скорости в каждой точке пространства остается постоянным, то такое движение называется установившимся, или стационарным . Линии тока в этом случае совпадают с траекториями частиц.

Часть жидкости, ограниченная линиями тока, называется трубкой тока . Вектор скорости будет касательным к поверхности трубки тока; следовательно, частицы жидкости при своем движении не пересекают стенок трубки тока.

Возьмем перпендикулярное к направлению скорости сечение трубки тока S (Рис. 1.6.2).

Рис. 1.6.2. Трубка тока

Предположим, что скорость движения частиц жидкости одинакова во всех точках этого сечения. За время dt через сечение S пройдут все частицы, расстояние которых от S в начальный момент времени не превышает значения vdt. Следовательно, за время dt через сечение S пройдет объем жидкости, равный Svdt, а за единицу времени через сечение S пройдет объем жидкости, равный Sv. Возьмем трубку тока, настолько тонкую, что в каждом ее сечении скорость можно считать постоянной. Если жидкость несжимаема (ее плотность одинакова и не изменяется), то количество жидкости между сечениями S₁ и S₂ (Рис.1.6.3) будет оставаться неизменным.

Рис. 1.6.3. К теореме о неразрывности струи

Отсюда следует, что объемы жидкости, протекающие за единицу времени через сечения S₁ и S₂, должны быть одинаковыми (считаем, что через боковую поверхность трубки тока частицы жидкости не проходят):

Данный результат представляет собой содержание теоремы о неразрывности струи . Из соотношения (1.6.1) следует, что при переменном сечении трубки тока частицы несжимаемой жидкости движутся с ускорением. В горизонтальной трубке тока (Рис.1.6.4) это ускорение может быть обусловлено только непостоянством давления вдоль оси трубки — в местах, где скорость меньше, давление должно быть больше, и наоборот.

Рис. 1.6.4. Изменение скорости струи

1.6.2. Уравнение Бернулли

Рассматривая движение жидкостей, во многих случаях можно считать, что перемещение одних частей жидкости относительно других не связано с трением. Жидкость, в которой внутреннее трение (вязкость) полностью отсутствует, называется идеальной.

Выделим в стационарно текущей идеальной жидкости трубку тока малого сечения (Рис.1.6.5). Рассмотрим малый объем жидкости, ограниченной стенками трубки тока и перпендикулярными сечениями S₁ и S₂. За время Δt этот объем переместится вдоль трубки тока (сечение S₁ переместится в положение S₁‘, пройдя путь Δl₁, сечение S₂ переместится в положение S₂‘, пройдя путь Δl₂). В силу неразрывности струи заштрихованные объемы будут иметь одинаковую величину: ΔV₁ = ΔV₂ =ΔV.

Рис. 1.6.5. К выводу уравнения Бернулли

Энергия каждой частицы жидкости складывается из ее кинетической энергии и потенциальной энергии в поле силы тяжести. Вследствие стационарности течения частица, находящаяся спустя время Δt в любой из точек незаштрихованного объема (например, в точке О), имеет такую же скорость, какую имела частица, находившаяся в той же точке в начальный момент времени. Поэтому приращение энергии ΔЕ можно вычислить как разность энергий заштрихованных объемов ΔV₁ и ΔV₂.

Возьмем сечение трубки тока и отрезки Δl настолько малыми, чтобы всем точкам каждого из заштрихованных объемов можно было приписать одно и то же значение скорости v, давления р и высоты h. Тогда приращение энергии запишется следующим образом (ρ — плотность жидкости):

В идеальной жидкости силы трения отсутствуют. Поэтому приращение энергии (1.6.2) должно равняться работе, совершаемой над выделенным объемом силами давления. Силы давления на боковую поверхность перпендикулярны в каждой точке к направлению перемещения частиц, к которым оно приложены, и работы не совершают. Отлична от нуля лишь работа сил давления, приложенных к сечениям S₁ и S₂:

Приравнивая (1.6.2) и (1.6.3), после упрощения получим:

Сечения S₁ и S₂ были взяты совершенно произвольно. Поэтому полученный результат можно сформулировать следующим образом: в стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие:

Данное соотношение носит наименование уравнения Бернулли . Несмотря на то, что оно получено в приближении идеальности жидкости, оно достаточно хорошо выполняется для реальных жидкостей, внутреннее трение в которых не слишком велико.

Пусть жидкость течет так, что скорость имеет во всех точках одинаковую величину. Тогда будет выполняться равенство:

откуда следует, что распределение давления в этом случае будет таким же, как и в покоящейся жидкости.

Для жидкости, текущей горизонтально, выполняется:

т.е. давление оказывается меньшим в тех точках, где скорость больше.

1.6.3. Силы внутреннего трения

Всем реальным жидкостям и газам присуща вязкость, или внутреннее трение. Вязкость проявляется в том, что возникшее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается.

Рассмотрим такой опыт. Пусть в жидкость погружены две параллельные друг другу пластины (Рис. 1.6.6), линейные размеры которых значительно превосходят расстояние d между ними.

Рис. 1.6.6. Внутреннее трение в жидкостях

Считаем нижнюю пластину неподвижной, а верхняя приводится в движение относительно нижней с некоторой скоростью v₀. Опыт показывает, что для перемещения верхней пластины с постоянной скоростью v₀ необходимо действовать на нее с вполне определенной постоянной силой . Поскольку пластина не получает ускорения, то действие этой силы уравновешивается равное по величине, но противоположно направленной силой .

Из опыта следует, что выполняется:

где S — площадь пластин, h — коэффициент пропорциональности, зависящий от природы и состояния жидкости, называемы коэффициентом внутреннего трения или коэффициентом вязкости.

Нижняя пластина при перемещении верхней пластины также оказывается подверженной действию силы , по величине равной силе . Чтобы нижняя пластина оставалась неподвижной, должно выполняться: . Воздействие пластин друг на друга осуществляется через жидкость, заключенную между пластинами, передаваясь от одного слоя к другому. Если в любом месте зазора провести плоскость, параллельную пластинам, то можно утверждать, что часть жидкости, лежащая над этой плоскостью, действует на часть жидкости, лежащую под плоскостью, с силой . Следовательно, соотношение (1.6.8) определяет не только силу трения, действующую на пластины, но и силу трения между соприкасающимися частями жидкости.

Если исследовать скорость частиц жидкости в разных слоях, то оказывается, что она изменяется в направлении z, перпендикулярном к пластинам, по линейному закону:

Действительно, частицы жидкости, непосредственно соприкасающиеся с пластинами, как бы прилипают к ним и движутся с той же скоростью, что и пластины. Из (1.6.9) следует:

Подставляя (1.6.10) в (1.6.8), имеем:

Следовательно, сила трения пропорциональна градиенту скорости.

Единицей вязкости в СИ является такая вязкость, при которой градиент скорости, равный 1 м/с на 1 м, приводит к возникновению силы внутреннего трения в 1 Н на 1 м&sup2 поверхности касания слоев (1 Н·с/м&sup2). В СГС единицей вязкости служит 1 пуаз (пз), равный такая вязкость, при которой градиент скорости, равный 1 см/с на 1 см, приводит к возникновению силы внутреннего трения в 1 дин на 1 см&sup2 поверхности касания слоев. 1 Н·с/м&sup2 = 10 пз.

Коэффициент вязкости зависит от температуры, причем у жидкостей вязкость сильно уменьшается с температурой, у газов, напротив, коэффициент вязкости с температурой возрастает. Такое различие указывает на различие механизма внутреннего трения в жидкостях и газах. При повышении температуры сильно возрастает подвижность молекул в жидкости, что и влечет уменьшение ее вязкости.

© ФГОУ ВПО Красноярский государственный аграрный университет, 2013

Уравнение неразрывности трубки тока жидкости

Гидродинамика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа.

Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.

Идеальная среда

Гидродинамика изучает поведение идеальной жидкости — воображаемой среды без вязкости, сил трения и теплопроводности. Касательные напряжения равны нулю. Её можно представить, как систему небольших упругих шаров с пренебрежимо малым объёмом, не прилипающих друг к другу. Они часто сталкиваются друг с другом. Поэтому каждый шар переносит при движении массу, импульс, момент импульса, энергию.

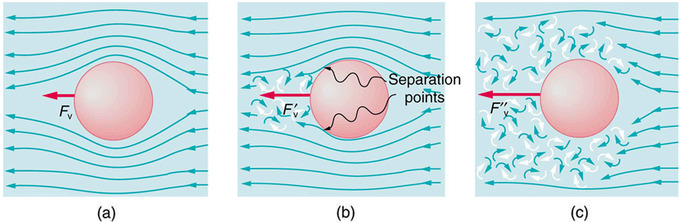
Ламинарное и турбулентное движения жидкости

Экспериментально установлено, что в природе существуют два различных вида движения потока — ламинарное (слоистое, упоря­доченное), при котором отдельные слои жидкости скользят друг относительно друга, и турбулентное (неупорядоченное), когда частицы жидкости движутся по сложным, все время изменяющимся траекториям.

Вследствие этого затрата энергии на турбулентное движение потока больше, чем на ламинарное.

Турбулентность — название такого состояния сплошной среды, газа, жидкости, их смесей, когда в них наблюдаются хаотические колебания мгновенных значений давления, скорости, температуры, плотности относительно некоторых средний значений, за счёт зарождения, взаимодействия и исчезновения в них вихревых движений различных масштабов. Происходит их нелинейное вихревое взаимодействие и распространение в пространстве и времени.

Турбулентность может возникать и при нарушении сплошности среды, например, при кавитации (кипении). При опрокидывании и разрушении волны прибоя возникает многофазная смесь воды, воздуха, пены. Мгновенные параметры среды становятся хаотичными.

Ламинарное течение

Отличие ламинарного течения от турбулентного состоит в характере и направлении водных (газовых) потоков. Они перемещаются слоями, не смешиваясь и без пульсаций. Другими словами, движение проходит равномерно, без беспорядочных скачков давления, направления и скорости.

Ламинарное течение жидкости образуется, например, в узких кровеносных сосудах живых существ, капиллярах растений и в сопоставимых условиях, при течении очень вязких жидкостей (мазута по трубопроводу). Чтобы наглядно увидеть струйный поток, достаточно немного приоткрыть водопроводный кран – вода будет течь спокойно, равномерно, не смешиваясь. Если краник отвернуть до конца, давление в системе повысится и течение приобретет хаотичный характер.

Движение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком. Графически движение жидкостей изображается с помощью линий тока. Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

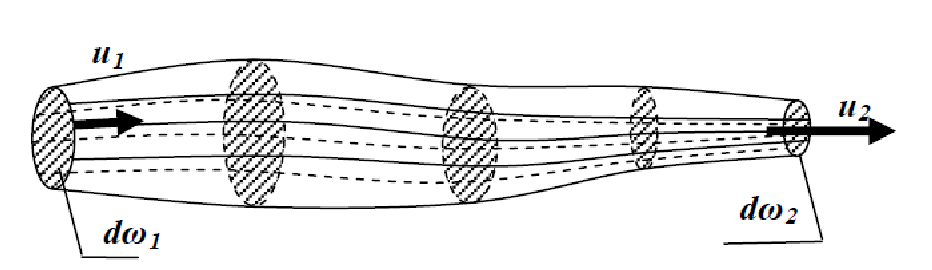
Трубка тока — трубчатая поверхность, ограниченная линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.

Для случая установившегося движения элементарной струйке придаются следующие свойства:

• форма элементарной струйки остается неизменной с течением времени;
• через стенки элементарной струйки движение жидкости не происходит (обмена энергией жидкости между элементарными струйками нет);
• вследствие малости поперечного сечения элементарной струйки скорость и гидродинамическое давление во всех точках ее поперечного сечения одинаковы.

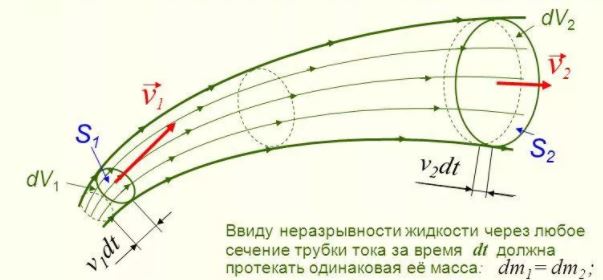
Уравнение неразрывности жидкости

В гидравлике обычно рассматривают потоки, в которых не образуются разрывы. Если выделить в потоке два любых сечения, отстоящих друг от друга на некотором расстоянии, то за время Δ t через сечение S проходит объем жидкости SvΔ t; следовательно, за 1 с через S 1 пройдет объем жидкости S 1 v 1 , где v 1 — скорость течения жидкости в месте сечения S 1 . Через сечение S 2 за 1 с пройдет объем жидкости S 2 v 2 , где v 2 — скорость течения жидкости в месте сечения S 2 . Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (ρ = const), то через сечение S 2 пройдет такой же объем жидкости, как и через сечение S 1 , т. е.

Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение называется уравнением неразрывности для несжимаемой жидкости.

Уравнение Бернулли

При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии.

Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.

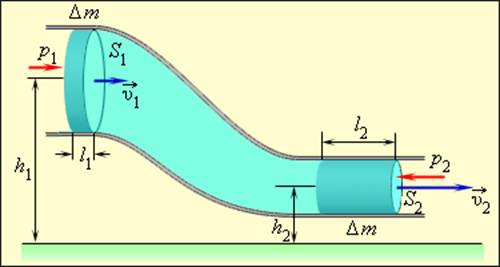
Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения. Различные части трубы могут находиться на разных высотах. У идеальной жидкости трение полностью отсутствует.

Выделим в стационарно текущей несжимаемой идеальной жидкости трубку тока, ограниченную сечениями S₁ и S₂, по которой жидкость течет слева направо. Пусть в месте сечения S₁ скорость течения v₁ давление р₁ и высота, на которой это сечение расположено, h₁. Аналогично, в месте сечения S₂ скорость течения v₂, давление р₂, высота сечения h₂. За малый промежуток времени Δt жидкость перемещается от сечения S₁ к сечениюS‘₁, от S₂ к S’₂.

Согласно закону сохранения энергии, изменение полной энергии Е₂ — Е₁ идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы т жидкости, где

— полные энергии жидкости массой т в местах сечений S₁ и S₂ соответственно.

С другой стороны, А — это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S₁ и S₂, за рассматриваемый малый промежуток времени Δt:

где р — статическое давление (давление жидкости на поверхность обтекаемого ею тела),

ρv 2 /2 — динамическое давление.

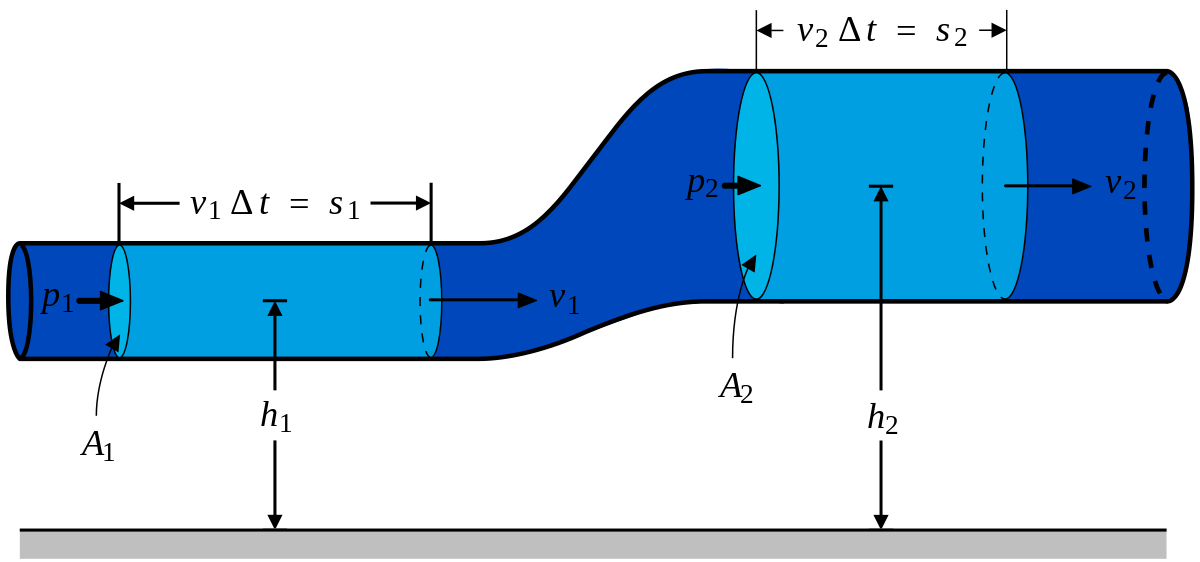
1. Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности следует, что при те чении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах, т. е. там, где скорость меньше.

Это можно продемонстрировать, установив вдоль трубы ряд манометров. В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.

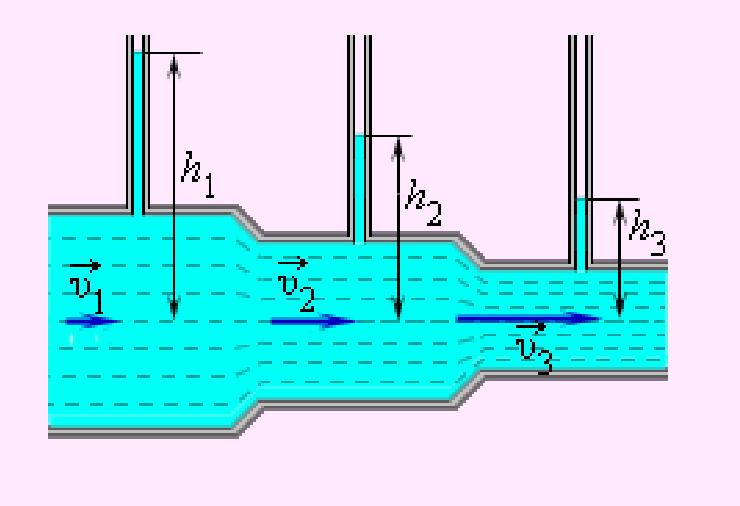
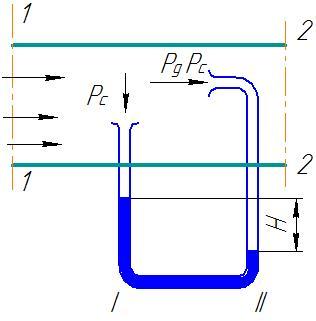
2. Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито — Прандтля. Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоединены к манометру. С помощью одной из трубок измеряется полное давление (р₀), с помощью другой — статическое (р).Манометром измеряется разность давлений:

где ρ — плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:

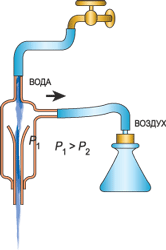
3. Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса. Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавливается и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст. = 133,32 Па).

4. Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие.

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₂ выхода ее из отверстия). Напишем для них уравнение Бернулли:

Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. p₁ = p₂ , то уравнение будет иметь вид

Из уравнения неразрывности следует, что v₂/v₁ = S₁/S₂, где S₁ и S₂ — площади поперечных сечений сосуда и отверстия. Если S₁>>S₂, то членом v 2 ₁/2 можно пренебречь и

Это выражение получило название формулы Торричелли .

Уравнение неразрывности и уравнение Бернулли.

Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.

Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.

Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.

Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.

Содержание статьи

Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.

Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υ_ср .

Таким образом уравнение расхода для потока будет

υ_ср – средняя скорость потока

F – площадь сечения потока.

Уравнение неразрывности потока жидкости

Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.

Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный

а через сечение 2-2 из него же вытекает объем, равный

Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.

Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.

Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки

Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что

т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.

Уравнение неразрывности струи жидкости. Уравнение Бернулли.

Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.

При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.

Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.

Если всё это записать в виде формулы, то

где W – приращение кинетической энергии = m * υ 2 / 2

ΣA – сумма работ действующих сил = P *ΔS

В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.

Теперь рассмотрим обе части этого выражения по порядку.

Приращение кинетической энергии ΔW

В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.

Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.

Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен

масса в этом случае получается равной

Подставляя все это в выражение для кинетической энергии получаем цепочку

ΔW = m * υ 2 ₂ / 2 — m * υ 2 ₁ / 2 = ρ * q * ΔТ * υ 2 ₂ / 2 — ρ * q * ΔТ * υ 2 ₁ / 2

Работа сил действующих на систему ΣA

Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести A_Т равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.

Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.

Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.

Силы давления А_Д , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.

Суммарно работа сил давления будет

Подставляя в начальное уравнение

Полученные выражения для ΔW и ΣA получаем

Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые

Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:

Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2

В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Видео по теме уравнение неразрывности

Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.

Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.

Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.