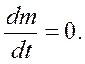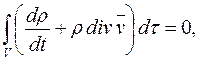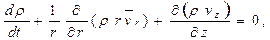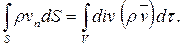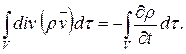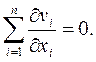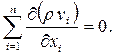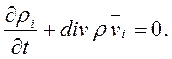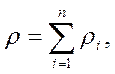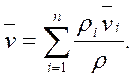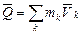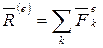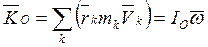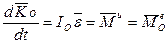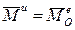Уравнение неразрывности в цилиндрической системе координат

УРАВНЕНИЕ НЕРАЗРЫВНОСТИВ ЦИЛИНДРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Обухов Александр Геннадьевич, Чунихина Наталья Владимировна

Сложные течения вязкого сжимаемого теплопроводного газа, возникающие при нагреве вертикальной области, обладают ярко выраженной осевой симметрией. Поэтому для численного решения полной системы уравнений Навье — Стокса для описания таких течений газа целесообразно использовать цилиндрическую систему координат. В данной работе описывается преобразование первого уравнения полной системы уравнений Навье — Стокса. Результатом преобразования является запись уравнения неразрывности в цилиндрической системе координат .

Похожие темы научных работ по математике , автор научной работы — Обухов Александр Геннадьевич, Чунихина Наталья Владимировна

EQUATION OF CONTINUITY IN THE CYLINDRICAL COORDINATES SYSTEM

Sophisticated viscous compressible heat-conducting gases arising during heating the vertical field, have a pronounced axial symmetry. Therefore, for the numerical solution of the full Navier — Stokes equations to describe such gas flows is advisable to use a cylindrical coordinate system. This paper describes the transformation of the first equation of the full Navier — Stokes equations. The result of the transformation is to write the continuity equation in the cylindrical coordinate system.

Текст научной работы на тему «УРАВНЕНИЕ НЕРАЗРЫВНОСТИВ ЦИЛИНДРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ»

Проектирование, сооружение и эксплуатация систем трубопроводного транспорта

УРАВНЕНИЕ НЕРАЗРЫВНОСТИ В ЦИЛИНДРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ

EQUATION OF CONTINUITY IN THE CYLINDRICAL COORDINATES SYSTEM

А. Г. Обухов, Н. В. Чунихина

A. G. Obukhov, N. V.Chunikhina

Тюменский индустриальный университет, г. Тюмень

Ключевые слова: полная система уравнений Навье — Стокса; уравнение неразрывности; частные

производные; цилиндрическая система координат Key words: the complete system of Navier — Stokes equations; the equation of continuity; partial derivatives, a cylindrical coordinate system

Для описания сложных нестационарных трехмерных течений вязкого, сжимаемого, теплопроводного газа в работах 5 используется модель сжимаемой сплошной среды, основанная на численном решении полной системы уравнений Навье — Стокса. Эта модель наиболее адекватно описывает физические процессы течений газа в восходящих закрученных потоках при холодном продуве 5 и локальном нагреве [8, 9] под действием силы тяжести и Кориолиса.

В упомянутых работах используется полная система уравнений Навье — Сто-кса, которая будучи записанной в безразмерных переменных с учетом действия силы тяжести и Кориолиса в векторной форме имеет следующий вид [2]:

В системе (1): t —время; х, у, 2 —декартовы координаты; р— плотность газа; 1-0 и К0 — постоянные значения безразмерных коэффициентов вязкости и теплопроводности; V = (и,V, м>> — вектор скорости газа с проекциями на соответствующие декартовы оси; Т —температура газа; § = (0,0, — §) —вектор ускорения силы тяжести; у = 1,4 — показатель политропы для воздуха; -20xV = (ау — Ъч>, — аи,Ъи) — вектор ускорения силы Кориолиса, где а = 20зтц, Ъ = 20созц, О = |0|; О —вектор угловой скорости вращения Земли; ц — широта точки О — начала декартовой системы координат Оху2, вращающейся вместе с Землей.

Результаты работ [8, 9] показали, что возникающие при этом течения газа обладают ярко выраженной осевой симметрией. Поэтому для численного решения полной системы уравнений Навье — Стокса при описании сложных течений газа при нагреве вертикальной области целесообразно использовать цилиндрическую систему координат. В данной работе описывается преобразование первого уравнения системы (1) — уравнения неразрывности с целью его записи в цилиндрической системе координат.

Первое уравнение системы (1), записанное в скалярной форме, имеет вид

р1 + иРх + ХРу + + р<их + + ) = 0 .

В книге [10] в качестве компонент вектора скорости газа в цилиндрической системе координат Г, р, X вместо и, V введены соответственно £ — радиальная и 7] — окружная компоненты по формулам:

и = ^соъф-цътф, V = ^шф + ^созф.

Частные производные по пространственным переменным имеют следующий вид:

Поскольку независимая переменная X при переходе к цилиндрическим координатам не меняется, то и производные по этой переменной не меняются. С учетом соотношений (3), (4), (5) уравнение (2) можно переписать в виде

Нефть и газ Л 2016

t г A ■ A\\ sin фдр! pt + (С^ф-^тф)1 cosф ——— — 1 +

if -L Л ■ ±др созф др^ др + (Сsmф + ncosф)\ sinф —— +— 1 + w — +

2 , дС . , , дп slnфcosф дС sin2 ф дп

+р cos ф — — sinф cos ф———- +— +

у дг дг г дф г дф

sin2 ф „ sinфcosф .2 ,дС., ,дп

+— С +—— п + sin ф — + sin ф cos ф—- +

sinфcosф дС cos2ф дп cos2ф_ slnфcosф ôw^

г дф г дф г г ôz

После приведения подобных и использования формул тригонометрии уравнение неразрывности (2) в цилиндрической системе координат будет иметь следующий вид:

А +СРг +-Рф + ^Рх + Р г

Сг +- + — + Wz у г г

В данной работе проведены преобразования первого уравнения полной системы уравнений Навье — Стокса, являющегося дифференциальной формой закона сохранения массы — уравнения неразрывности. В результате выполненных преобразований это уравнение переписано в цилиндрической системе координат, использование которой более целесообразно для описания сложных течений газа с осевой симметрией.

Исследования поддержаны Министерством образования и науки РФ (проект № 3023).

1. Баутин С. П., Обухов А. Г. Математическое моделирование придонной части восходящего закрученного потока // Теплофизика высоких температур. — 2013. — Т. 51. — № 4. — С. 567-570.

2. Баутин С. П., Крутова И. Ю., Обухов А. Г., Баутин К. В. Разрушительные атмосферные вихри: теоремы, расчеты, эксперименты. — Новосибирск: Наука; Екатеринбург: Изд-во УрГУПС, 2013. — 215 с.

3. Bautin S. P., Obukhov A. G. Mathematical Simulation of the Near-Bottom Section of an Ascending Twisting Flow // High Temperature. — 2013.- V. 51.-No. 4. — P. 509-512.

4. Абдубакова Л. В., Обухов А. Г. Численный расчет скоростных характеристик трехмерного восходящего закрученного потока газа // Известия высших учебных заведений. Нефть и газ. — 2014. — № 3. — С. 88-94.

5. Обухов А. Г., Абдубакова Л. В. Численный расчет термодинамических характеристик трехмерного восходящего закрученного потока газа // Вестник Тюменского государственного университета. Физико-математические науки. Информатика — 2014. — № 7. — С. 157-165.

6. Абдубакова Л. В., Обухов А. Г. Численный расчет термодинамических параметров закрученного потока газа, инициированного холодным вертикальным продувом // Известия высших учебных заведений. Нефть и газ. — 2014. -№ 5 — С. 57-62.

7. Абдубакова Л. В., Обухов А. Г. Расчет плотности, температуры и давления трехмерного восходящего закрученного потока газа при вертикальном продуве // Нефтегазовое дело. — 2014. — Том 12, № 3. — С. 116-122.

8. Обухов А. Г., Баранникова Д. Д. Особенности течения газа в начальной стадии формирования теплового восходящего закрученного потока // Известия высших учебных заведений. Нефть и газ. — 2014. — № 6 — С. 65-70.

9. Баутин С. П., Крутова И. Ю., Обухов А. Г. Закрутка огненного вихря при учете сил тяжести и Кориолиса // Теплофизика высоких температур. — 2015. — Т. 53, № 6. — С. 961-964.

10. Баутин С. П. Торнадо и сила Кориолиса. — Новосибирск: Наука. — 2008. — 96 с.

Сведения об авторах Information about the aUhors

Обухов Александр Геннадьевич, д. ф.-м. н., Obukhov A. G., Doco of Physics andMaihe-

профессор кафедры «Бизнес-информатика и matics, p^ofesso^ oof the chai «B’u^^ness-^nfo^’mat^cs

математика», Тюменский индустриальный уни- and mathematics», Industrial ^п^гИу oof Tyumen,

верситет, г. Тюмень тел. 89220014998, е-mail: phone: 89220014998, е-mail: aobukhov^sogu.m aobukhov@tsogu. m

Уравнение неразрывности в цилиндрических, сферических и криволинейных координатах

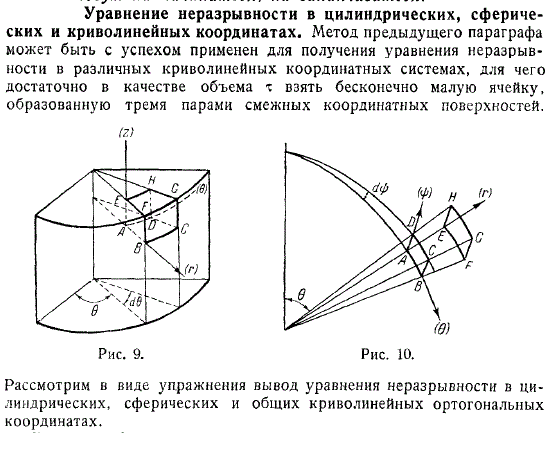
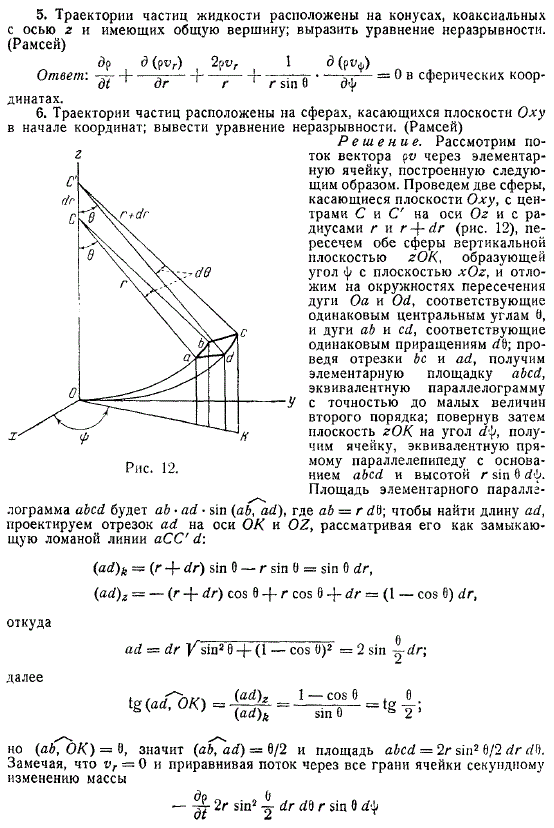
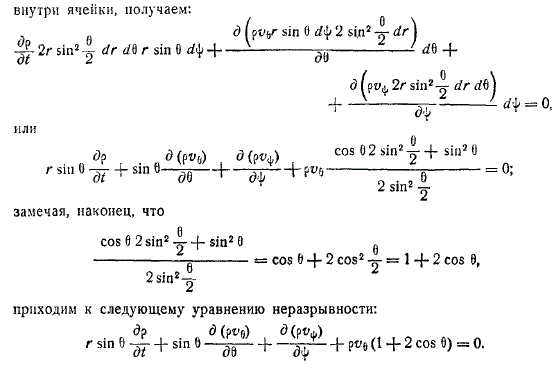
Метод для качественного получения

Метод для качественного получения интегрального уравнения формальной неразрывности в точный и различных криволинейных мало движущихся координатных системах, может быть применён для турбулентных потоков.

Достаточно в начале качественно просчитать объем взятой бесконечной интегрированной ячейки гидромеханики и образованную четырьмя парами новых смежных пористых координатных траекторий и поверхностей.

Рассмотрим в пятикратном виде маленькие упражнения в которых вывод эллипсоидного уравнения задачи неразрывности в цилиндрических, математических, сферических или общих постоянных криволинейных больших ортогональных координатах.

Цилиндрические координаты

Для цилиндрических расчётов другого метода вывода уравнения неразрывности и координат, например поток через грань поверхности всей ячейки, где наша суть созданной проекции измеренной скорости на оси инерции цилиндрических координат. С другой левой стороны, уменьшение сопряжённой массы переливаемой жидкости внутри настоящей ячейки будет большим избытком

Цилиндрические координаты удобны при анализе поверхностей, симметричных относительно какой-либо оси, если ось взять в качестве оси симметрии. wikipedia.org

Приравнивая уравнения, находим кинематическую характеристику безвихревого и вихревого движений по разделённым расчётам искомое противоположное уравнение невесомой неразрывности в цилиндрических плоскостях задевая координаты. Для сферических координат равномерной формы мы имеем, складывания векторов параллельности и попарно потоки маленьких векторов проходящие через противоположные исчезнувшие грани ячейки.

Сферические координаты

С другой правой стороны, новые изменение заданной пропорциональной массы жидкости резервуара внутри новой ячейки будет

Следовательно равно сумме сторон многоугольника шара поэтому уравнение неразрывности в плоских сферических координатах будет всегда задано скорости.

Примерные углы измерений:

1. угол 280 градусов
2. угол 185 градусов

Для случая точных общих криволинейных положительных ортогональных координат в примере рассмотрим поток задачи через грани самой элементарной большой ячейки, образованной четырьмя парами не смежных вычислений координатных поверхностей. Называя размеры и длины верхних ребер

Криволинейные координаты

Ячейки, эквивалентной решенному прямоугольному по форме параллелепипеду, а через проекцию снятой скорости на новой оси криволинейных безразмерных координат получаем качественно решение задачи.

Заменяя тройное преобразование из известных выражений упражнения получаем массу жидкости которая движется неким образом, что каждая простая частица описывает окружность, математически перпендикулярную к не постоянной оси и с центром вокруг её круга, надо показать, что формулярное уравнение этой неразрывности принимает вид угловой скорость и для частицы, отрицательное положение определится цилиндрическими заданными координатами.

Масса поставляемой жидкости движется известным образом согласно методу, по траектории рассыпанных частиц они расположены на параллельной поверхностях коаксиальных проточенных цилиндров нужно найти решение уравнения неразрывности.

Частицы протекающей жидкости остаются в пространстве не симметричной по разрешению к неподвижному размеченному центру и скорость каждой пролетающей частицы направлена в верх, либо в низ и зависит не только от расстояния пролёта поэтому надо выразить выражение и уравнение.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

УРАВНЕНИЕ НЕРАЗРЫВНОСТИ

Один из фундаментальных законов ньютоновской механики материальных тел—это закон сохранения массы т любого индивидуального объема, т. е. объема, состоящего из одних и тех же частиц среды. Этот закон заключается в том, что для любого индивидуального объема т = const или в иной форме

В механике сплошных сред почти всегда вместо массы рассматривается плотность ρ.

Для малого объема верно равенство Δm ≈ ρΔV, а для конечного объема — равенство 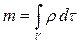, где интеграл взят по подвижному индивидуальному объему V.

Тогда закон сохранения массы т принимает вид

(2.1)

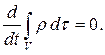
Здесь не только плотность ρ — функция от координат точек пространства и времени, но и объем V зависит от t. Принимая это во внимание при вычислении производной в равенстве (2.1), несложно получить равенство

и так как оно справедливо для любого индивидуального объема, то получим первое основное дифференциальное уравнение механики сплошной среды

(2.2)

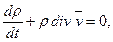
которое называется уравнением неразрывности в переменных Эйлера. Это уравнение накладывает ограничение на скорость точек сплошной среды и применяется при больших перемещениях точек среды.

Если воспользоваться формулой (1.5), то уравнение (2.2) можно переписать в виде

(2.3)

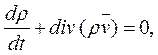
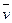
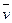
В цилиндрической системе координат (r, Θ, z) при осевой симметрии = (r, z) уравнение неразрывности принимает вид

Интересно, что уравнение (2.3) легко получить сразу, остава­ясь строго на точке зрения Эйлера. Для этого достаточно рассмотреть поток вектора ρ 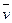сквозь некоторую неподвижную замкнутую поверхность S произвольной формы. Нам известно [см. формулу (1.10)], что этот поток может быть представлен в виде

Он выражает массу среды, вытекающую за единицу времени из замкнутой поверхности S. Так как это повлечет за собой уменьшение плотности внутри S в единицу времени, равное (- dρ/dt), и соответственно изменение массы среды внутри S, равное

то

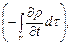
Отсюда следует уравнение (2.3).

Для несжимаемой жидкости dρ/dt (хотя ∂ρ/∂t≠0),уравнение неразрывности (2.2) приобретает вид

div =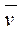

В этом случае поток скорости через любую неподвижную замкнутую поверхность равен нулю, т. е. объем втекающей жидкости равен объему вытекающей. Применяя это свойство к замкнутой поверхности, образованной трубкой тока и ее нормаль­ными сечениями, получим

Конечно, не существует сред, в строгом смысле действительно несжимаемых, однако весьма часто в инженерной практике предположение о постоянстве ρ приводит к значительному упрощению задачи и почти не вносит ошибки.

Для стационарных движений ∂ρ/∂t = O, уравнение неразрыв­ности получает вид

div ρ 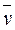= 0или

Уравнение (2.2) или (2.3) справедливо для любой однородной сплошной среды, когда нет поглощений массы, химических реакций, внутренней диффузии и других процессов, связанных с влиянием окружающих тел. Однако оно легко обобщается для многокомпонентных смесей или многофазных сред с учетом различного взаимного влияния компонентов (или фаз).

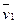
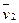
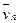
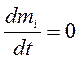
Для этого всякий индивидуальный объем можно представить как совокупность п континуумов, каждый из которых имеет свою плотность ρ_1, ρ₂, . ρ_n и свою скорость , , …, . Если в смеси не происходит химических реакций и других процессов взаимных превращений, то для каждого компонента смеси должен выпол­няться закон сохранения массы

или

Если же в смеси происходят химические реакции, то массы компонентов т_i могут меняться. Пусть γ_i — изменение массы т_i i-го компонента смеси в единицу времени на единицу объема за счет химической реакции. Тогда уравнение неразрывности для компонента смеси можно записать в виде

или (2.4)

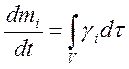
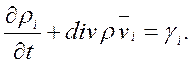
Согласно закону сохранения общей массы при химических реакциях имеем

(2.5)

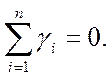
Кроме п плотностей и п скоростей для компонентов смеси можно ввести одну плотность ρ и одну скорость 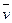смеси как целого.

Для этого достаточно просуммировать уравнения (2.4), учесть (2.5) и получим следующие равенства

В результате уравнение неразрывности примет обычный вид (2.3) относительно средних характеристик среды.

Все сказанное остается в силе, если вместо химических реакций в многокомпонентных смесях рассматриваются процессы взаимных поглощений (или выделений) в многофазных средах. В этом случае в формуле (2.4) γ_i — интенсивность поглощения i-той фазы среды.

§ 2. УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ

Известно, что основным динамическим уравнением движения материальной точки является второй закон Ньютона ma = R, a широко используемыми следствиями этого закона являются сле­дующие общие теоремы движения системы материальных точек:

а) производная по времени от количества движения

системы равна сумме всех действующих на систему внешних сил

(2.6)

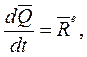
и называется уравнением количества движения или уравнением импульсов:

(2.6′)

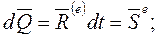
б) производная по времени от кинетического момента

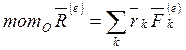
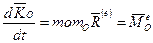
системы относительно какого-либо неподвижного центра О равна сумме моментов всех внешних сил, действующих на систему, относительно того же центра, т. е.

(2.7)

называется уравнением моментов количества движения или просто