Уравнение нулевой линии при изгибе
§1 Понятие изгиба. Нейтральная линия.
О
К
В зависимости от возникающих в балке внутренних силовых факторов (ВСФ) различают чистый и поперечный изгиб (рис. 6.3).
Чистым изгибом называется изгиб, при котором в сечении балки возникает только изгибающий момент, а поперечным называется изгиб, при котором действуют как изгибающий момент, так и поперечная сила.
К
ак показывают расчеты нейтральная линия проходит через главную центральную ось сечения, расположенную перпендикулярно к силовой линии.
Нейтральную линию иногда называют нулевой линией, т.к. в ее точках нормальные напряжения и продольные деформации отсутствуют (σ = 0; ε = 0).
§2 Напряжения при чистом и поперечном изгибе.
Основное условие прочности.
В теории изгиба принимаются такие допущения:
1) Справедлива гипотеза плоских сечений.
2) По высоте сечения бруса волокна не имеют веса, т.е. не давят друг на друга. Принимается упрощенная схема напряженного состояния.
3
) по ширине сечения бруса напряжения являются постоянными.
С учетом принятых допущений и рассматривая четыре стороны задачи для чистого изгиба, при котором возникают только нормальные напряжения можно использовать следующую расчетную зависимость.
г
сечения бруса, находящейся на
расстоянии y под нейтральной
Mизг – изгибающий момент в данном
Ix – осевой момент инерции сечения
y – ордината последней точки.
Анализируя зависимость (15.1) можно заключить, что нормальное напряжение изменяется по линейному закону, увеличиваясь от центра сечения к его краям. Причем максимальные напряжения, возникающие в крайних волокнах можно определить по известной формуле:
где 
Зависимость (15.1) и (15.2) графически можно представить в виде следующей эпюры напряжений (рис. 6.8).
П
Расчет на прочность при чистом изгибе производится по следующему условию прочности
Условие (15.3) является основным условием прочности при изгибе. При помощи этого условия можно выполнить известные виды расчетов: проверочный, проектировочный и максимальной нагрузки.
– проверочный по (15.3)
При расчете на прочность балок из разных материалов необходимо учитывать их способность сопротивляться растягивающим и сжимающим напряжениям. При этом следует придерживаться следующих рекомендаций:

1. Если балка изготовлена из пластичного материала, одинаково работающего на растяжение-сжатие, т.е. ([σр] = [σc]), то целесообразно использовать сечения, симметричные относительно нейтральной линии. В этом случае на прочность проверяются крайние точки сечения балки σmax = |σmin| (рис.6.9).
2
§3 Главные напряжения при изгибе.
Полная проверка прочности балок при изгибе
В 
Решая обратную задачу можно найти положение главной площадки и величины главных напряжений (σ1, σ3).
Анализируя напряженное состояние при изгибе для опасных точек балки и используя (16.3)-(16.6) можно выполнить полную проверку прочности балки при изгибе, для этого необходимо рассмотреть три типа опасных точек в разных сечениях исследуемой балки. Проведем т0акую проверку, выбрав следующую расчетную схему (рис. 6.15)
Полная проверка прочности балки при изгибе выполняется по трем типам опасных точек. Опасная точка I типа: по длине балки находится сечения, где действует максимальный по модулю изгибающий момент (сечение I-I), а по высоте балки – в крайних волокнах от нейтральной линии, где имеют место максимальные нормальные напряжения (точки 1 и 5). В этих точках имеет место линейное напряженное состояние. Условие прочности для точек I типа имеет такой вид (основное условие прочности)
О
пасные точки II типа располагаются по длине балки в сечениях с максимальной поперечной силой (сечение II-II левое и правое), а по высоте балки – на уровне нейтральной линии (точка 3 левая и правая), где действует максимальное касательное напряжение. В этих точках возникает частный случай плоского напряженного состояния – чистый сдвиг. Условие прочности имеет такой вид
Опасные точки III типа располагаются в сечениях балки, где возникает неблагоприятное сочетание больших изгибающего момента и поперечной силы (сечение III-III левое и правое), а по высоте балки – между крайними волокнами и нейтральной линией, где одновременно большие нормальные и касательные напряжения (точки 2 и 4 левая, правая). в этих точках возникает упрощенное плоско-напряженное состояние. Условие прочности для точек III типа записывается согласно теории прочности (например, для пластичного материала: по III или IV теории).
Если по мере выполнения расчетов прочность по одному из условий не выполняется, то необходимо увеличить размеры сечения балки или увеличить номер профиля согласно таблиц сортамента.
Приведенный выше анализ напряженного состояния балок при изгибе позволяет грамотно конструировать элементы сооружений и рационально выбирать их поперечные сечения, например, для железобетонных конструкций целесообразно использовать стальную арматуру и располагать её по линиям, совпадающим с траекторией главных растягивающих напряжений.
§4 Деформации при изгибе. Общие понятия.
В теории изгиба расчет на прочность в большинстве случаев выполняется расчетом на жесткость. В этом случае оценивается упругая податливость балки и определяются такие её размеры, чтобы возникающие деформации не превышали допустимых пределов, т.е. условие жесткости можно представить в таком виде
где fmax – максимальная расчетная деформация;
[f] – допускаемая деформация.
Рассмотрим основные элементы деформированного состояния балки (рис.6.16).
у
y – прогиб – вертикальное перемещение, отсчитываемое перпендикулярно к исходной оси балки;
u – горизонтальное перемещение или смещение балки (обычно бесконечно малая величина, ≈ 0);
θ – угол поворота сечения к заданной точке.
П
Правило знаков для y:
Правило знаков для θ:
против часовой стрелки «+»,
по часовой стрелке «–».
Для левой системы координат наоборот.
Между прогибом и углом поворота существует дифференциальная зависимость, которую можно получить рассматривая координаты некоторой плоской кривой (рис.6.18).

При нахождении линейных или угловых деформаций для реальных балок необходимо знать её уравнение упругой линии УУЛБ (уравнение упругой линии балки), имеющее такой общий вид:
Рассмотрим некоторые методы нахождения деформаций при изгибе, основанные на составлении и решении уравнения упругой линии балки.
§5 Дифференциальное уравнение упругой линии балки и его интегрирование.
Из теории изгиба известна зависимость кривизны балки следующего вида
С другой стороны из курса высшей математики кривизна плоской кривой может быть представлена через её координаты следующим образом:
Приравнивая (18.3) и (18.4) получим точное ДУУЛБ
Полученное дифференциальное уравнение имеет большие трудности при решении, поэтому его упрощают, учитывая известную гипотезу малости деформаций
Учитывая небольшие углы поворота сечений для реальных балок получаем следующее приближенное ДУУЛБ, которое будет называться в дальнейшем основным дифференциальным уравнением упругой линии балки.
Данное уравнение справедливо для правой системы координат.
Полученное уравнение решается путем двойного интегрирования
В этом решении произвольные постоянные интегрирования представляют собой по геометрическому смыслу соответственно угол поворота и прогиб в начале координат
Произвольные постоянные интегрирования определяются из граничных или начальных условий построения расчетной схемы балки. Рассмотрим основные разновидности граничных условий.
Виды граничных условий

Рассмотренный выше метод расчета перемещений при изгибе называется методом непосредственного интегрирования дифференциального уравнения упругой линии балки МНИ ДУУЛБ.
Для его применения необходимо:
- Выбрать систему координат (в крайнем сечении балки)
- Для каждого силового участка балки составляется общее уравнение моментов, которое подставляется в основное ДУУЛБ.
- Решается ДУУЛБ путем двойного интегрирования и определяется произвольная постоянная интегрирования из граничных условий.
- В полученное уравнение упругой линии балки подставляются поочередно абсциссы искомых точек и определяются прогибы. Аналогично находятся углы поворотов с использованием дифференциальной зависимости (18.1).
МНИ обладает существенным недостатком, который заключается в том, что для решения балок с большим количеством силовых участков необходимо определить большое количество произвольных постоянных интегрирования (например, для n участков будет 2n таковых), поэтому данный метод целесообразно использовать только для балок, имеющих один или два участка. Для устранения названного недостатка предлагается более совершенный метод, основанный на ДУУЛБ и более рациональном его решении.
§6 Метод начальных параметров.
Универсальное уравнение упругой линии балки (УУУЛБ).
В отличие от предыдущего метода в предлагаемом методе ДУУЛБ составляется таким образом, что независимо от количества силовых участков балки приходится находить только две произвольных постоянных интегрирования – прогиб и угол поворота в начале координат (y0, θ0). Это достигается путем применения специальных правил при составлении уравнения моментов или уравнений прогибов. В этом случае все решение сводится к составлению УУУЛБ применительно к заданной расчетной схеме балки.
Общий вид УУУЛБ будет следующим:
После дифференцирования (18.13) получим универсальное уравнение углов поворота балки УУУЛБ.
где y0, θ0 – геометрические начальные параметры, т.е. прогиб и угол поворота в начале координат, определяются по граничным условиям;
М0, Q0 – статические начальные параметры, т.е. изгибающий момент и поперечная сила в начале координат; они определяются по условиям нагружения или по уравнениям равновесия.
Mi, Fi, qi – момент, сосредоточенная сила и распределенная нагрузка в i том сечении балки соответственно. Они включаются в уравнение со своими знаками в соответствии с «правилом зонтика» для изгибающего момента.
ki – величина, характеризующая неравномерно распределенную нагрузку, например, треугольную или трапециевидную.
Д
ля решения задач по нахождению перемещений в балках методом начальных параметров необходимо (пример: рис.6.23):
2) Для последнего силового участка балки составляется универсальное уравнение упругой линии балки УУУЛБ.
Для составления выражения для распределенной нагрузки её предварительно продолжают до конца (последнего) сечения и вводят дополнительную компенсирующую нагрузку обратного направления.
3) Определяются начальные параметры УУУЛБ.
Геометрические начальные параметры.
Статические начальные параметры.
4) Подставляются все найденные начальные параметры в исходное УУУЛБ и путем дифференцирования получается универсальное уравнение углов поворота балки УУУЛБ.
В этом же пункте определяются искомые перемещения, для чего в соответствующее уравнение подставляется абсцисса искомой точки и отбрасываются слагаемые, характеризующие внешние нагрузки, которые находятся за пределами рассматриваемого участка.
Рассмотренный метод начальных параметров является достаточно простым и универсальным, но имеет следующие недостатки.
1) Он не применим для балок с ломаной осью, рамным систем и кривых брусьев.
2) Не позволяет определить перемещение в произвольных направлениях, кроме вертикального.
Для устранения этих недостатков в курсе сопротивления материалов широко применяются так называемые энергетические способы, основанные на известном законе сохранения энергии.
§7 Потенциальная энергия упругой деформации (ПЭУД)
в общем случае нагружения бруса. Теорема Кастильяно.
На основании закона сохранения энергии работа внешних сил на перемещениях точек системы равна потенциальной энергии упругой деформации
Основываясь на положениях этого закона можно зная величину энергии, накопленной брусом, найти перемещение ее точек при известных внешних нагрузках. Получим общую зависимость для ПЭУД произвольного бруса, находящегося под воздействием разнообразных внешних нагрузок, для этого составим сумму работ, совершаемых шестью внутренними силовыми факторами.
Учитывая известное выражение работ для простых деформаций получим следующее выражение
kx, ky – безразмерные коэффициенты, характеризующие форму сечения бруса при сдвиге.
Для нахождения перемещений с помощью ПЭУД применяется так называемая теорема Кастильяно:
Обобщенные перемещения в точке приложения некоторой обобщенной нагрузки представляют собой частную производную потенциальной энергии по заданной обобщенной нагрузке.
где δk – обобщенное перемещение в точке К, где приложена внешняя обобщенная нагрузка, по ее направлению.
FK – обобщенная нагрузка, действующая в точке К.
Под обобщенным перемещением понимается перемещение, вызываемое соответствующей обобщенной нагрузкой. В частности,
Д
анная теорема обладает тем недостатком, что позволяет находить только перемещения, соответствующие данной обобщенной нагрузке, только в точке её приложения и только по ее направлению.
§8 Метод для нахождения перемещений в упругих системах.
Н едостатки теоремы Кастильяно можно устранить, если использовать прием, предложенный Мором-Максвеллом. Этот метод основан на применении так называемой фиктивной обобщенной нагрузки Φ.
едостатки теоремы Кастильяно можно устранить, если использовать прием, предложенный Мором-Максвеллом. Этот метод основан на применении так называемой фиктивной обобщенной нагрузки Φ.
1) В заданной точке системы прикладывается соответствующая обобщенная параметром фиктивная нагрузка, которая условно принимается равной единице.
Направление приложения фиктивной нагрузки соответствует искомому направлению. Для прогиба удобно единичную силу направлять снизу вверх согласно положительному направлению прогиба (см. правило знаков для прогиба). Единичный момент направляется против часовой стрелки в соответствии с положительным направлением угла поворота.
2) Определяется потенциальная энергия упругой деформации всей системы, которая подставляется в зависимость , выражающую теорему Кастильяно и производится расчет частной производной по данной фиктивной нагрузке.
В полученном выражении исключается фиктивная нагрузка, т.к. ее на самом деле нет.
Для удобства практического расчета все преобразования рассмотренные выше исключаются и расчет перемещений выполняется по формуле, называемой интегралом Мора (запишем применительно к деформации изгиба).
где 

Р
Выбирается вспомогательная схема, которая загружается соответствующей единичной нагрузкой. Чтобы взять вспомогательную схему, надо на исходной схеме отбросить все внешние нагрузки.
Для исходной и вспомогательной схем составляются общие выражения изгибающих моментов по всем участкам, которые подставляются в интеграл Мора.
Метод Мора является самым сильным по возможности расчета перемещений (его можно применить для любой схемы), однако его недостатком является высокая трудоемкость при расчете систем с большим количеством силовых участков.
Для сокращения сложности таких расчетов интеграл Мора обычно заменяют операцией умножения согласно способа Верещагина (1924 г.).
§9 Способ Верещагина и его применение
П
Согласно способа Верещагина искомое перемещение представляет собой произведение площади грузовой эпюры на ординату единичной эпюры, которая располагается под центром тяжести грузовой эпюры на данном участке.

где ωi – площадь грузовой эпюры на i том участке.

Рассмотрим пример (рис.6.28)
При использовании способа Верещагина для упрощения расчетов можно учитывать следующие рекомендации.
1) При перемножении эпюр, имеющих линейные очертания можно использовать площадь одной из них, а ординату другой в прямом и обратном порядке.
2
3
4
5
Способ Верещагина является достаточно удобным и простым для расчета перемещений в упругих системах при любых видах деформаций. Однако его нельзя применить для систем, имеющих криволинейные участки.
§10 Статически неопределимые системы при изгибе.
Каноническое уравнение метода сил (КУМС).
Статически неопределимая система (СНС) при изгибе обладает теми же свойствами, что СНС при растяжении-сжатии и кручении, однако имеют следующую особенность.
Степень неопределимости в таких системах может быть образована как внешними, так и внутренними признаками построения СНС.
Система неопределима внешним образом, если её элементы имеют ограничения по перемещению в пространстве. Такие ограничения накладываются опорными связями и в этом случае степень СНС по внешним признакам находится по известной формуле
где R – число неизвестных реакций опор СНС,
У – число уравнений статики.
Степень СНС образована внутренними признаками, если они накладывают ограничения на относительные перемещения точек системы по отношению друг к другу. К ним относятся дополнительные элементы, шарниры, узлы и прочие геометрические факторы.
В этом случае степень СНС по внутренним признакам находится по следующей формуле
где K – число замкнутых контуров СНС (например, рамок),
У – число шарниров, врезанных в элемент СНС в пересчете на простые шарниры.
П
ростым называется шарнир, в котором сходятся только два стержня.
Сложный шарнир, в котором сходятся более 3 х стержней можно заменить n–1 простыми шарнирами (n – число стержней, сходящихся в сложном шарнире).
Таким образом, степень СНС можно определить сложив зависимости (21.1) и (21.2).
Для решения СНС при изгибе в курсе сопротивления материалов применяются метод сил, метод перемещений и комбинированный метод. Наиболее часто применяется метод сил, в частности прием сравнения перемещений, канонические уравнения метода сил (КУМС) и уравнения трех моментов.
Удобно и математически относительно несложно провести решение СНС с применением КУМС.
Д
ля составления канонических уравнений устанавливается число лишних связей системы. Эти лишние связи (например, реакции опор) обозначаются буквами Xi независимо от того сила это или момент (рис.6.34)
Для каждой лишней опоры составляется уравнение деформаций в виде суммы перемещений, вызванных действиями всех лишних связей и внешних нагрузок, причем эти деформации на опорах должны равняться нулю. Для удобства записи и решения эти уравнения составляются по определенному правилу (или канону).
В общем случае КУМС записывается так:
где δij – перемещение в i той точке под действием единичной силы, приложенной к j той точке.
δ11, δ22, δ33, . δnn – главные коэффициенты КУМС, представляющие собой единичные перемещения в i той точке под действием единичной силы, приложенной в той же точке. Они определяются по способу Верещагина путем перемножения эпюр от единичных сил «самих на себя».
δ12, δ13, . δij – побочные коэффициенты, представляющие собой единичные перемещения, определяемые по способу Верещагина путем перемножения единичных эпюр между собой.
Δ1F, Δ2F, . ΔnF – грузовое перемещение, определяемое как перемещение в i той точке под действием системы внешних нагрузок.
По способу Верещагина оно находится путем перемножения грузовой эпюры момента на единичную эпюру под действием i той единичной силы.
Определив все единичные и грузовые перемещения КУМС, решается данная система и определяются неизвестные усилия X1; X2; X3 . Xi . Xn.
По завершении раскрытия неопределимости СНС строятся необходимые эпюры (для рамы – N, Q и M). и выполняются две проверки – статическая и деформационная.
Статическая проверка заключается в проверке равновесия элементов или узлов системы (см. задачу № 12 РПР-2).
Деформационная проверка сводится к расчету перемещений тех точек системы, где действуют лишние связи (Xi). Обычно проверяется равенство нулю перемещений в опорах системы. Для этого необходимо по способу Верещагина перемножить конечную эпюру изгибающих моментов с единичной эпюрой, построенной для i той лишней связи.
В 
В следующем случае система рассекается по оси симметрии и в качестве лишних связей выбираются внутренние силовые факторы в проведенном сечении.
Тогда единичные эпюры от соответствующих внутренних силовых факторов будут иметь либо симметричную, либо кососимметричную формы
Следовательно, при перемножении симметричной эпюры на кососимметричную получаем перемещение равное нулю.
Блестящим планам везет на проектировщиков, скверным планам везет на исполнителей. Веслав Брудзиньский
ещё >>
Укажите правило знаков для изгибающих моментов в общем случае сложного сопротивления стержня
Mz имеет положительное значение , если растягиваются нижние волокна, в противном случае Mz имеет отрицательное значение.
My имеет положительное значение , если растягиваются дальние (правые, если смотреть на сечение со стороны положительного направления оси OX) волокна.My имеет отрицательное значение , если растянуты ближние ( левые , если смотреть на сечение со стороны положительного направления оси OX) волокна.
4. Какой вид сопротивления стержня называется косым изгибом? Виды косого изгиба.
Косой изгиб –такой случай изгиба, когда плоскость действия суммарного изгибающего момента проходит через центр тяжести сечения , но не совпадает ни с одной из главных плоскостей инерции сечения.
Косой изгиб делится на плоский косой изгиб и на пространственный косой изгиб.
Плоский косой изгиб имеет место, когда все поперечные нагрузки действуют в плоскости, не совпадающей с главными плоскостями инерции.
Пространственный косой изгиб имеет место при действии поперечных нагрузок в различных плоскостях.
5. Запишите уравнение нулевой линии для случая косого изгиба. Как определить положение нулевой линии? Правила знаков для силовой и нулевой линий.
Mz*y0/Jz +My*z0/Jy=0 или 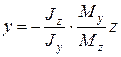
Положение нулевой линии определяется исходя из следующей формулы:

Если αр больше нуля , то силовая линия повёрнута относительно оси OY против часовой стрелки, если меньше нуля, то по часовой.
Если α0 меньше нуля , то нулевая линия повёрнута относительно оси ОZ против часовой стрелки, если больше нуля ,то по часовой.
6. Как определить величину и направление полного прогиба при косом изгибе?
Формулы прогибов по осям при косом изгибе: 
Формула суммарного прогиба балки при косом изгибе: 
Направление результирующего перемещения (f) задаётся значением угла наклона ( 

Направление суммарного прогиба балки при косом изгибе перпендикулярно нулевой линии при косом изгибе.
7. Какой вид сопротивления стержня называется внецентренным сжатием (растяжением)? Какие внутренние усилия при этом возникают? По какой трансформированной формуле определяются напряжения σx при внецентренном сжатии?
Внецентренное сжатие ( растяжение ) это вид деформации стержня , при котором результирующая внешней нагрузки направлена вдоль продольной оси стержня, не совпадает с ней.
При этом возникают следующие внутренние усилия : N = – P , Mz = – P yP My = – P zP ,
где уР, zP – координаты точки приложения силы.
Напряжение определяется по формуле : 
8. Что такое ядро сечения? Какое практическое значение имеет определение ядра сечения?
Ядро сечения – это выпуклая область, содержащая центр тяжести сечения и обладающая тем свойством, что при нахождении точки приложения силы внутри этой области или на её границе во всех точках сечения напряжения имеют одинаковый знак.
Определение ядра сечения позволяет определить область сечения при приложении силы в точках которой всё сечение будет работать на сжатие. Это нужно постольку поскольку такие материалы как бетон, кирпич плохо сопротивляются растяжению.
Нулевая линия делит сечение на две части: на одной стороне, возникают сжимающие напряжения, а на другой растягивающие.
Косой изгиб.
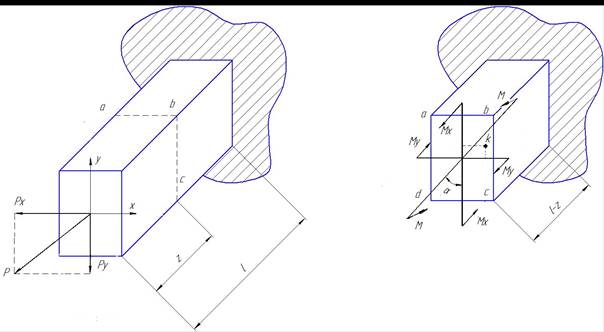
Деформация косого изгиба возникает при действии нагрузок не проходящих через главные оси инерции поперечного сечения.
Силу Р раскладываем на составляющие Рх и Ру: 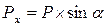
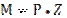
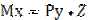
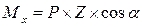
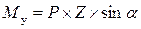
Нормальные напряжения в любой точке К с координатами (Хк;YK). Получим на основе принципа независимости действия сил, как сумму напряжений от Мх и Му, действующих по главным осям инерции:
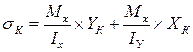 | (1) |
| Напряжения в угловых точках будут определяться по формулам: | 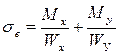 ; ; 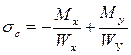 ; ; 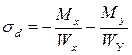 ; ; 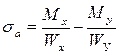 . . |
В формулу (1) представим в другом виде: 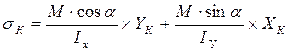
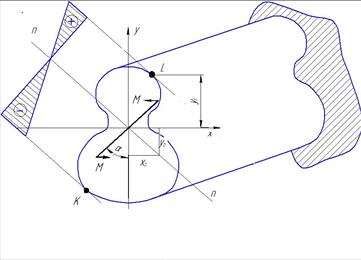 | В начале находится положение нулевой линии, т.е. геометрического места точек, где нормальные напряжения равны нулю. 1)Предположим, что нулевая линия проходит через (nn). 2)Затем, учитывая, что по мере удаления от нулевой линии напряжения возрастают, заключаем, что наиболее опасными точками являются точки L и K. 3)Проводим через L и K линии, параллельные линии (nn) и строим эпюру σ. |
Для определения положения нулевой линии (nn) правую часть формулы (2) приравняем к нулю: 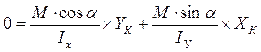
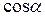
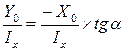
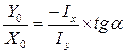
| (3)По формуле (3) находится положение нулевой линии. Вывод: если 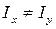 , то , то 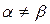 , это означает, что угол наклона нулевой линии не перпендикулярен к линии действия нагрузки. , это означает, что угол наклона нулевой линии не перпендикулярен к линии действия нагрузки. | |||||||||||||||||||||||
| Наибольшие напряжения будут в точках L и K. Прочность стержня проверяется по формулам: |
| |||||||||||||||||||||||
 Для симметричного сечения условие прочности можно записать так: Прогиб при косом изгибе находится как геометрическая сумма двух прогибов: Для симметричного сечения условие прочности можно записать так: Прогиб при косом изгибе находится как геометрическая сумма двух прогибов: |
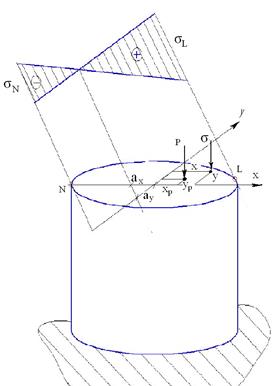
где Внецентренное сжатие (растяжение). Если сжимающая сила не проходит через центр тяжести поперечного сечения стержня, то стержень будет испытывать внецентренное сжатие (растяжение).
По формуле (1) можно найти напряжение в любой точке поперечного сечения для этого следует координаты X и У подставить с учетом их знака.
Формула (1) справедлива также и при растяжении. В этом случае вместо (-) имели бы (+) перед формулой, где : Найдем положение нулевой линии. Для этого приравняем правую часть формулы (1) к нулю.
Поэтому для нахождения положения нулевой линии найдем отрезки, отсекаемые ею на осях Х и У. Для чего принимаем у=0 ; х=ах. подставив в уравнение получим
Примем
Нулевая линия делит сечение на две части: на одной стороне, возникают сжимающие напряжения, а на другой растягивающие. Прочность при внецентренном сжатии (растяжении) проверяется по формулам:
Ядро сечения – это область, очерченная вокруг центра тяжести и обладающая теми свойствами, что если приложить внутри этой области силу, то все поперечное сечение стержня будет иметь напряжение одинакового знака. Для построения ядра сечения следует провести несколько линий касающихся контура сечения, вычислить для этих линий aх и aу, а затем найти значения Пример1. Найти ядро сечения для прямоугольника.
Дата добавления: 2016-02-13 ; просмотров: 2224 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ источники: http://mydocx.ru/11-30001.html http://helpiks.org/7-2774.html |



















































 едостатки теоремы Кастильяно можно устранить, если использовать прием, предложенный Мором-Максвеллом. Этот метод основан на применении так называемой фиктивной обобщенной нагрузки Φ.
едостатки теоремы Кастильяно можно устранить, если использовать прием, предложенный Мором-Максвеллом. Этот метод основан на применении так называемой фиктивной обобщенной нагрузки Φ.



























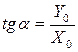
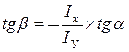
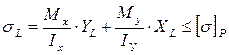 (или ≤ Rр)
(или ≤ Rр) 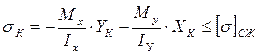 (или ≤ Rсж)
(или ≤ Rсж)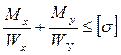 (или ≤R)
(или ≤R)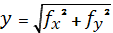
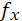 – прогиб в плоскости оси Х от силы Рх ;
– прогиб в плоскости оси Х от силы Рх ; 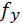 – прогиб в плоскости оси У от силы Ру.
– прогиб в плоскости оси У от силы Ру.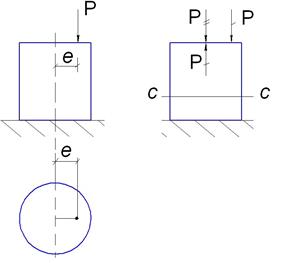
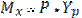 напряжения будут
напряжения будут 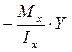 .От момента
.От момента 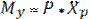 имеем напряжение
имеем напряжение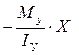 . Суммарное напряжение равно:
. Суммарное напряжение равно: 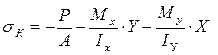
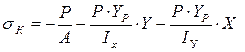
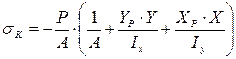
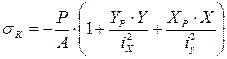 (1)
(1)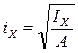 ;
; 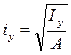
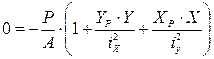 ;
; 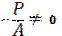 ; значит
; значит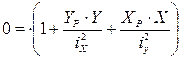
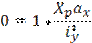
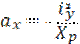 — отрезок отсекаемый нулевой линией на оси Х.
— отрезок отсекаемый нулевой линией на оси Х.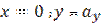 , получим
, получим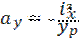 — отрезок отсекаемый нулевой линией на оси У.
— отрезок отсекаемый нулевой линией на оси У.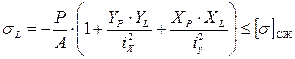 (или ≤Rcж).
(или ≤Rcж). 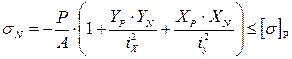 (или ≤Rр), где ХL и YL — координаты точки L; ХN и УN — координаты точки N.
(или ≤Rр), где ХL и YL — координаты точки L; ХN и УN — координаты точки N.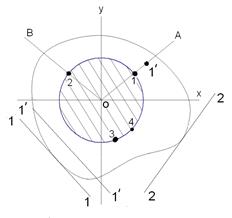
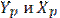 . Если сила приложена в точке 1 / ; то нулевая линия пройдет по (1 / ;1 / ). Если точку приложения силы перемещать вдоль луча ОА, то нулевая линия будет также перемещаться, оставаясь параллельно самой себе. Таким образом можно найти такую точку 1 для которой нулевая линия коснётся контура сечения будет (1;1). Таким же образом можно на луче ОВ найти точку 2, для которой нулевая линия пройдет по (2;2). В итоге приняв несколько точек 1;2;3;4… и соединив их получим ядро сечения.
. Если сила приложена в точке 1 / ; то нулевая линия пройдет по (1 / ;1 / ). Если точку приложения силы перемещать вдоль луча ОА, то нулевая линия будет также перемещаться, оставаясь параллельно самой себе. Таким образом можно найти такую точку 1 для которой нулевая линия коснётся контура сечения будет (1;1). Таким же образом можно на луче ОВ найти точку 2, для которой нулевая линия пройдет по (2;2). В итоге приняв несколько точек 1;2;3;4… и соединив их получим ядро сечения.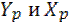 по формулам:
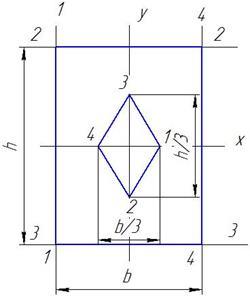
по формулам: 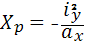 ;
; 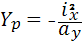
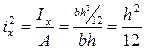
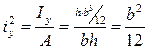 Проведем линию (1-1):
Проведем линию (1-1): 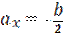 ;
; 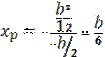
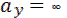 ;
; 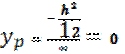 Линия (2-2):
Линия (2-2): 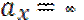 ;
; 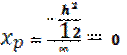
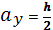 ;
; 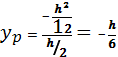 Аналогично получаем 3 и 4 точки.
Аналогично получаем 3 и 4 точки.