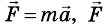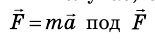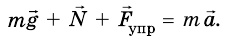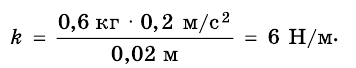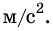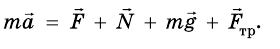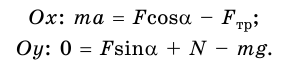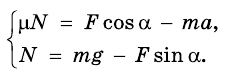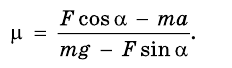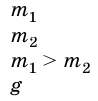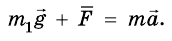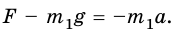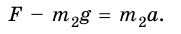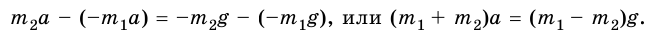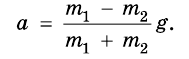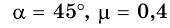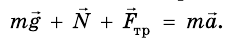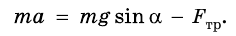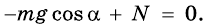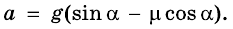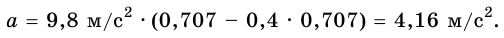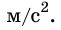Движение тела под действием нескольких сил в физике — определение и формулы с примерами
Движение тела под действием нескольких сил:
B 7-м классе вы рассматривали движение тела, на которое действует только одна сила — сила упругости, сила притяжения или сила трения. В действительности такие движения в земных условиях почти никогда не происходят. Это следует уже из того, что рядом с силами упругости или тяготения всегда действует сила трения.
Вам известно, что если тело движется равномерно прямолинейно, то на него действуют силы, которые компенсируются. Если к телу приложены несколько сил и равнодействующая сила будет направлена в сторону движения, то тело будет двигаться равноускоренно, а если в противоположную сторону — равнозамедленно.
Если решать задачи по механике, когда на тело действует несколько сил, то следует напомнить, что в уравнении, которое выражает второй закон Ньютона
Начиная решать задачу, надо сначала выбрать направление координатных осей и изобразить на рисунке векторы всех сил и вектор ускорения тела, если известно его направление. Потом надо найти проекции всех векторов на эти оси координат. Наконец, записать уравнение второго закона Ньютона для проекций на каждую ось и решить вместе найденные уравнения.
Часто бывает так, что в движении участвуют несколько тел, так или иначе связанных между собой, как говорят, система тел. Примером такого движения может быть движение спортсмена на водных лыжах, который направляется за катером, или движение грузов на нити, переброшенных через блок. При этом на каждое из тел могут действовать несколько сил. Как в таких случаях решать задачи? Общий порядок решения задач остается таким, как рассматривали ранее. Только его надо применить к каждому из тел системы: уравнение второго закона Ньютона записывают для каждого из тел системы сначала в векторной форме, а потом в скалярной (для проекций) и решают вместе найденные уравнения.
В случае, если сумма сил, действующих на тело, равна нулю в формуле
Пример №1
Пружина одним концом прикреплена к бруску массой 0,6 кг, который расположен на гладком горизонтальном столе. Свободный конец пружины начали перемещать прямолинейно вдоль стола с ускорением 0,2 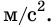
а = 0,2
Выполним рисунок.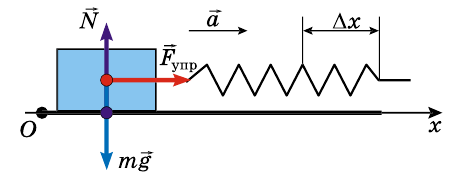
На брусок действуют: сила тяжести 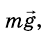
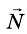
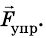
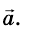
Запишем второй закон Ньютона в векторной форме:
Выберем ось Ох и найдем проекции векторов. Учитывая, что 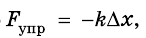
имеем: 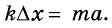
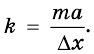
Подставив значения известных величин, определим:
Ответ: жесткость пружины равна 6 Н/м.
Пример №2
По горизонтальной дороге тянут за веревку под углом 30° груз, общая масса которого 80 кг. Сила натяжения 50 Н. Определите коэффициент трения скольжения, если груз движется с ускорением 0,15
На груз действуют силы: сила тяжести 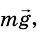
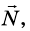
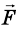
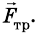
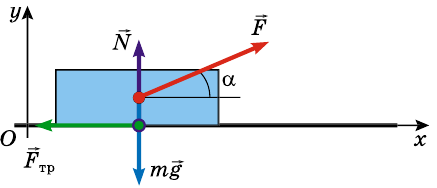
Запишем второй закон Ньютона для груза в векторной форме:
В проекциях на координатные оси данное уравнение имеет вид:
Поскольку 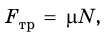
Подставим выражение mg — Fsina в первое уравнение вместо N, и выразим переменную:
Учитывая значения известных величин, вычислим:
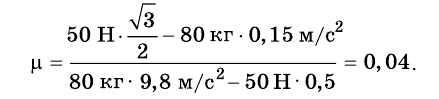
Полученное значение коэффициента трения скольжения приблизительно совпадает с табличными данными. Значит, задача решена правильно.
Ответ: 
Пример №3
Через неподвижный блок перекинута нить, к концам которой прикреплены тела массами 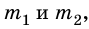
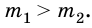
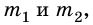
Дано:
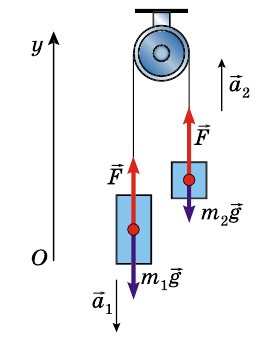
В этой задаче в движении участвуют два тела.
Если систему тел привести в движение, то тело массой 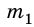
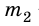
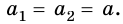
Координатную ось Оу направим по вертикали вверх.
На тело массой 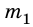
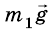
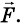
Из рисунка видно, что проекция 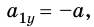
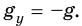
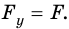
На тело массой 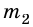
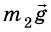
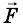
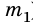
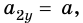
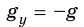
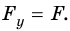
Вычтем из второго уравнения первое:
Таким образом, для ускорения а имеем:
Зная, что разность 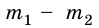
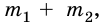
Блоки иногда и используются для того, чтобы заставить тело падать с ускорением, меньшим g. На этом основывается применение противовеса в лифтах и других подъемных механизмах.
Пример №4
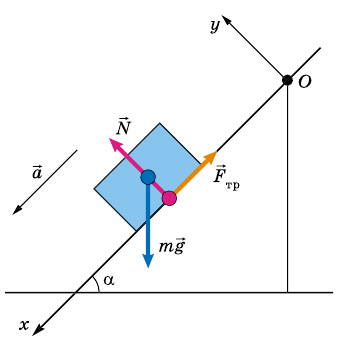
Тело движется вниз по наклонной плоскости, угол наклона которой 45° к горизонту. Коэффициент трения 0,4. Определите ускорение движения тела.
На это тело действует Земля, притягивающая его с силой 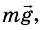
Кроме того, на тело действует наклонная плоскость с силой 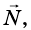
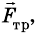
и записи условия задачи выполним рисунок.
Запишем второй закон Ньютона в векторной форме:
В этом случае координатные оси удобнее всего направить вдоль наклонной плоскости и перпендикулярно к ней. В этом случае перемещения вдоль оси Оу при движении не будет, а следовательно, ускорение 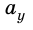
Запишем второй закон Ньютона в проекциях на координатные оси.
Проекция силы 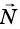
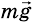
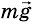
Проекция силы 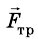
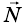
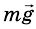
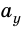
Эти два уравнения содержат неизвестные: т, a, N, 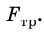
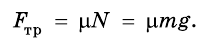
Учтя все выражения, получим уравнение: 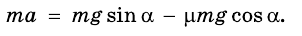
Сократив на m, получим:
Подставив значение, определим ускорение движения тела: а
Ответ: 4,16
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Наклонная плоскость в физике
- Давление газов и жидкостей
- Движение жидкостей и газов
- Гидравлические машины в физике
- Механическое давление в физике
- Столкновения в физике
- Рычаг в физике
- Блоки в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Нелинейные системы и уравнения
В более общем случае мы имеем не одно уравнение (1), а систему нелинейных уравнений $$ \begin
Метод Ньютона
Решение нелинейных уравнений
При итерационном решении уравнений (1), (3) задается некоторое начальное приближение, достаточно близкое к искомому решению \( x^* \). В одношаговых итерационных методах новое приближение \( x_
В итерационном методе Ньютона (методе касательных) для нового приближения имеем $$ \begin
Вычисления по (4) проводятся до тех пор, пока \( f(x_k) \) не станет близким к нулю. Более точно, до тех пор, пока \( |f_(x_k)| > \varepsilon \), где \( \varepsilon \) — малая величина.
Простейшая реализация метода Ньютона может выглядеть следующим образом:
Чтобы найти корень уравнения \( x^2 = 9 \) необходимо реализовать функции
Данная функция хорошо работает для приведенного примера. Однако, в общем случае могут возникать некоторые ошибки, которые нужно отлавливать. Например: пусть нужно решить уравнение \( \tanh(x) = 0 \), точное решение которого \( x = 0 \). Если \( |x_0| \leq 1.08 \), то метод сходится за шесть итераций.
Теперь зададим \( x_0 \) близким к \( 1.09 \). Возникнет переполнение
Возникнет деление на ноль, так как для \( x_7 = -126055892892.66042 \) значение \( \tanh(x_7) \) при машинном округлении равно \( 1.0 \) и поэтому \( f^\prime(x_7) = 1 — \tanh(x_7)^2 \) становится равной нулю в знаменателе.
Проблема заключается в том, что при таком начальном приближении метод Ньютона расходится.
Еще один недостаток функции naive_Newton заключается в том, что функция f(x) вызывается в два раза больше, чем необходимо.
Учитывая выше сказанное реализуем функцию с учетом следующего:
- обрабатывать деление на ноль
- задавать максимальное число итераций в случае расходимости метода
- убрать лишний вызов функции f(x)
Метод Ньютона сходится быстро, если начальное приближение близко к решению. Выбор начального приближение влияет не только на скорость сходимости, но и на сходимость вообще. Т.е. при неправильном выборе начального приближения метод Ньютона может расходиться. Неплохой стратегией в случае, когда начальное приближение далеко от точного решения, может быть использование нескольких итераций по методу бисекций, а затем использовать метод Ньютона.
При реализации метода Ньютона нужно знать аналитическое выражение для производной \( f^\prime(x) \). Python содержит пакет SymPy, который можно использовать для создания функции dfdx . Для нашей задачи это можно реализовать следующим образом:
Решение нелинейных систем
Идея метода Ньютона для приближенного решения системы (2) заключается в следующем: имея некоторое приближение \( \pmb
Таким образом, \( k \)-я итерация метода Ньютона состоит из двух стадий:
1. Решается система линейных уравнений (СЛАУ) \( \pmb
2. Находится значение вектора на следующей итерации \( \pmb
Для решения СЛАУ можно использовать приближенные методы. Можно также использовать метод Гаусса. Пакет numpy содержит модуль linalg , основанный на известной библиотеке LAPACK, в которой реализованы методы линейной алгебры. Инструкция x = numpy.linalg.solve(A, b) решает систему \( Ax = b \) методом Гаусса, реализованным в библиотеке LAPACK.
Когда система нелинейных уравнений возникает при решении задач для нелинейных уравнений в частных производных, матрица Якоби часто бывает разреженной. В этом случае целесообразно использовать специальные методы для разреженных матриц или итерационные методы.
Можно также воспользоваться методами, реализованными для систем линейных уравнений.
Законы Ньютона
Ньютон первым обратил внимание на силу, как причину, по которой тела приходят в движение и меняют свою скорость.
Раздел механики, изучающий силы, называется динамикой. По-гречески «динамис», значит «сила».
Что такое сила
Тела действуют друг на друга с помощью сил.
Сила – это мера взаимодействия тел. Измеряя силу, мы измеряем величину взаимного действия тел. В обыденной жизни мы говорим: «как сильно» одно тело действует на другое тело.
Смысл законов Ньютона
Ньютон, в своих законах динамики, хотел сказать следующее:
- В I законе: Если сила не действует, скорость не меняется. Импульс тела тоже не меняется.
- Во II законе: Если сила действует, скорость меняется. Импульс тела, также, меняется, появляется ускорение.
- В III законе: Взаимодействуют два тела — возникают две силы. Они по модулю равны, а по направлению противоположны.
Примечание:
Выражение «векторы равны по модулю», понимаем так: «длины векторов одинаковые».
Перед изучением законов Ньютона рекомендую вспомнить, что такое инерциальные системы отсчета (откроется в новой вкладке).
Первый закон Ньютона
Словесная формулировка первого закона Ньютона:
В инерциальной системе отсчета тело свою скорость не меняет, если на него не действуют другие тела (или действие других тел скомпенсировано).
Формула:
\( F = 0 \) – сила на тело не действует (Может быть и так: на тело действуют несколько сил, но их действие компенсируется);
\( a = 0 \) – ускорение отсутствует;
\( v = const \) – скорость тела не изменяется (остается одной и той же);
\( p = const \) – импульс тела не изменяется (остается одним и тем же);
Важно! По первому закону Ньютона, «двигаться с одной и той же скоростью по прямой» и «покоиться» — это равнозначные виды движения.
Значит, если на тело не действуют другие тела (силы), то
- тело будет двигаться с одной и той же скоростью по прямой, если оно так двигалось до этого,
- или будет продолжать покоиться, если покоилось в прошлом.
Второй закон Ньютона
Сформулируем словами второй закон Ньютона:
Ускорение, приобретаемое телом,
прямо пропорционально
приложенной силе
и обратно пропорционально
массе этого тела.
Формула второго закона Ньютона с пояснениями
\( a \left( \frac<\text<м>>
\( m \left( \text <кг>\right) \) – масса тела
\( F \left( H \right) \) – сила, которую приложили к телу
Примечание: Ускорение отвечает на вопрос: «Как быстро меняется скорость тела?». Значит, если изменяется хотя бы одна из характеристик вектора скорости, ускорение есть. А если скорость не изменяется, ускорения нет \( \vec < a >= 0 \)
Ускорение прямо пропорционально силе:
Чем больше сила, тем больше ускорение тела, тем быстрее тело меняет скорость.
Ускорение обратно пропорционально массе:
Чем больше месса тела, тем труднее изменить его скорость.
Формулу второго закона часто записывают в векторном виде:
Мы можем заменить местами правую и левую части, в таком случае получим:
Расшифруем эту запись: Возьмем вектор «F», умножим его на скаляр (1/m) и получим новый вектор «a».
Дробь \( \displaystyle \frac<1>
Примечания:
- Вместо слов «направлены в одну и ту же сторону» физики пользуются термином «сонаправлены». Лично мне удобнее пользоваться первой формулировкой.
- Часто применяют еще один вид записи, его называют так: «Второй закон Ньютона в импульсной форме».
Третий закон Ньютона
Пусть одно тело действует на второе тело. Тогда это второе тело будет в ответ действовать на первое.
Словами третий закона Ньютона можно сформулировать так:
Силы взаимного действия по модулю равны, а направлены противоположно. Они лежат на прямой, которая соединяет центры тел, действующих друг на друга.
\( F_ <12>\left( H \right) \) – сила, с которой первое тело действует на второе тело.
\( F_ <21>\left( H \right) \) – сила, с которой второе тело отвечает первому.
Пояснить формулу можно с помощью такого рисунка:
Обратите внимание, что длины красного и черного векторов равны.
Не важно, перед каким из векторов находится знак «минус». Этот знак показывает, что векторы направлены в противоположные стороны. Поэтому, формулу третьего закона Ньютона можно записать и так:
Примечания:
- Если перед каким-либо вектором записан знак «минус», то этот вектор развернут в противоположную от выбранной нами сторону.
- Между векторами находится знак равенства. Это значит, что длины векторов одинаковые (векторы по модулю равны).
Советую прочитать еще две статьи. Так как для решения задач кроме знания трех законов Ньютона нужно дополнительно уметь:
- находить проекции вектора на оси и
- составлять векторные силовые уравнения (ссылки открываются в новых вкладках).
http://slemeshevsky.github.io/num-mmf/snes/html/._snes-FlatUI001.html
http://formulki.ru/mehanika/zakony-newtona