Уравнение обратной функции f x x3

Взаимно обратные функции

Функция, обратная данной

По определению (см. §34 справочника для 7 класса)

Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.

Пусть некоторое соответствие задано таблицей:

Множество значений X = <-4;-3;…;4>отображается в множество значений Y = <-2;-1,5;…;2>: $X \xrightarrow Y$. При этом каждому значению x соответствует единственное значение y, т.е., данное соответствие f является функцией.

С другой стороны, мы можем рассмотреть обратное отображение $Y \xrightarrow X$, заданное той же таблицей. При этом каждому значению y соответствует единственное значение x, т.е., обратное соответствие $g = f^<-1>$ также является функцией.

Функцию $f: X \xrightarrow Y$ с областью определения X и областью значений Y называют обратимой , если обратное ей соответствие $g: Y \xrightarrow g X$ также является фунцией.

Если функция f обратима, то обратное ей соответствие $g = f^<-1>$ называют обратной функцией к f.

Например: аналитическое выражение для функции $X \xrightarrow Y$, заданной таблицей $y = f(x) = \frac<2>$. Обратное соответствие $Y \xrightarrow X$ также является функцией x = g(y) = 2y.

Функция g — обратная функция к f.

В общем случае формулы функций записывают в виде y(x). При такой записи, функции $y = \frac<2>$ и y=2x являются взаимно обратными.

Алгоритм вывода формулы функции, обратной данной

На входе: множества X и Y, для которых оба соответствия $X \xrightarrow Y$ и $Y \xrightarrow X$ являются функциями.

Шаг 1. В формуле для исходной функции заменить обозначения аргумента и значения: $x \rightarrow y$, $y \rightarrow x$.

Шаг 2. Из полученной формулы выразить y(x). Искомое выражение для обратной функции найдено.

Шаг 3. Учесть ограничения для области определения и области значений исходной и/или обратной функций.

1) Пусть исходная функция $y = \frac<2>$

Шаг 1. Меняем аргумент и значение: $x = \frac<2>$

Шаг 2. Находим y из полученной формулы: y = 2x — искомая обратная функция

Шаг 3. Ограничений на x и y нет

2) Пусть исходная функция y = -2x+3

Шаг 1. Меняем аргумент и значение: x = -2y+3

Шаг 2. Находим y из полученной формулы: $y = \frac<-x+3><2>$ — искомая обратная функция

Шаг 3. Ограничений на x и y нет

3) Пусть исходная функция $y = \sqrt$

Шаг 1. Меняем аргумент и значение: $x = \sqrt$

Шаг 2. Находим y из полученной формулы: $y = x^2-1$ — искомая обратная функция

Шаг 3. На исходную функцию накладываются ограничения

на $x:x+1 \ge 0 \Rightarrow x \ge -1$, на $y:y \ge 0$

Тогда исходная функция определяется на множествах $y \ge -1$, $x \ge 0$

4) Пусть исходная функция $y = 2x^2+1$

Шаг 1. Меняем аргумент и значение: $x = 2y^2+1$

Шаг 2. Находим y из полученной формулы: $y = \sqrt<\frac<2>>$ — искомая обратная функция

Шаг 3. На обратную функцию накладываются ограничения

на $x:x-1 \ge 0 \Rightarrow x \ge 1$, на $y:y \ge 0$

Тогда исходная функция определяется на множествах $y \ge 1$, $x \ge 0$

Исходная функция — парабола получает ограничения из-за обратной функции; только в этом случаи функции будут взаимно обратными.

Свойства взаимно обратных функций

Пусть f и g — взаимно обратные функции. Тогда:

1. Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.

2. Функции f и g либо одновременно возрастающие, либо одновременно убывающие.

3. Если f — нечётная, то и g — нечётная.

4. Графики f и g симметричны относительно биссектрисы 1-й четверти y = x.

5. Справедливы тождества f(g(x) ) = x и g(f(x) ) = x.

Графики пар взаимно обратных функций, найденных выше:

Примеры

Пример 1. Задайте формулой функцию, обратную данной.

Меняем аргумент и значение: x = 5y-4

Получаем: $y = \frac<5>$ — искомая обратная функция

Меняем аргумент и значение: x = -3y+2

Получаем: $y = \frac<-x+2><3>$ — искомая обратная функция

в) y = 4x+1, где $-1 \le x \le 5$

Меняем аргумент и значение: x = 4y+1

Требуем, чтобы: $-1 \le y \le 5 \Rightarrow -1 \le \frac <4>\le 5 \Rightarrow -4 \le x-1 \le 20 \Rightarrow -3 \le x \le 21$

Итак, искомая обратная функция: $y = \frac<4>$, где -3 $\le x \le 21$

г) $y=- \frac<1> <2>x+7$, где $2 \le x \le 9$

Меняем аргумент и значение: $x=-\frac<1> <2>y+7$

Получаем: y = 2(-x+7) = -2x+14

Требуем, чтобы: $2 \le y \le 9 \Rightarrow 2 \le -2x+14 \le 9 \Rightarrow -12 \le -2x \le -5 \Rightarrow$

$6 \ge x \ge 2,5 \Rightarrow 2,5 \le x \le 6$

$y = -2x+14,где 2,5 \le x \le 6$ — искомая обратная функция

Пример 2. Найдите функцию, обратную данной.

Постройте график исходной и обратной функции в одной системе координат.

$x = y^2 \Rightarrow y = \pm \sqrt$

При этом $y \le 0$

$y = — \sqrt$ – искомая обратная функция

б) y = x-3, $-1 \le x \le 4$

$x = y-3 \Rightarrow y = x+3$

При этом $-1 \le y \le 4 \Rightarrow -1 \le x+3 \le 4$

$\Rightarrow -4 \le x \le 1$

y = x+3, $-4 \le x \le 1$ — искомая обратная

$x = \frac<1> \Rightarrow y = \frac<1> -1$

Область определения: $x \ge 3$

Область значений: $y \ge 1$

$x = 1+ \sqrt \Rightarrow y = (x-1)^2+3$

Как найти обратную функцию

Многие приложения в алгебре и исчислении зависят от знания того, как найти обратную функцию, и это тема данного руководства.

Прежде всего, вам нужно понять, что перед тем, как найти инверсию функции, вы должны убедиться, что такая инверсия существует.

Преимущество метода поиска обратного, который мы будем использовать, заключается в том, что мы найдем обратное и выясним, существует ли оно одновременно.

Готовый?? Тогда пристегнитесь.

Как узнать, есть ли у функции инверсия?

Технически функция имеет инверсию, когда она взаимно однозначна (инъективна) и сюръективна.

Однако решающим условием является то, что она должна быть взаимно однозначной, потому что функцию можно сделать сюръективной, ограничив ее диапазон своим собственным изображением.

Как узнать, что функция взаимно однозначна?

Что ж, есть как минимум пара способов. Один из них — алгебраический, а другой — графический (держу пари, я знаю, какой из них вы предпочитаете, да?)

Алгебраический путь

Для алгебраического подхода, чтобы функция \(f\) была взаимно однозначной, нам нужно доказать, что каждый раз, когда это \(f(x) = f(y)\), нам нужно иметь это \(x = y\).

Другими словами, нам нужно доказать, что

\[f(x) = f(y) \,\,\Rightarrow \,\, x = y\]

Графический способ

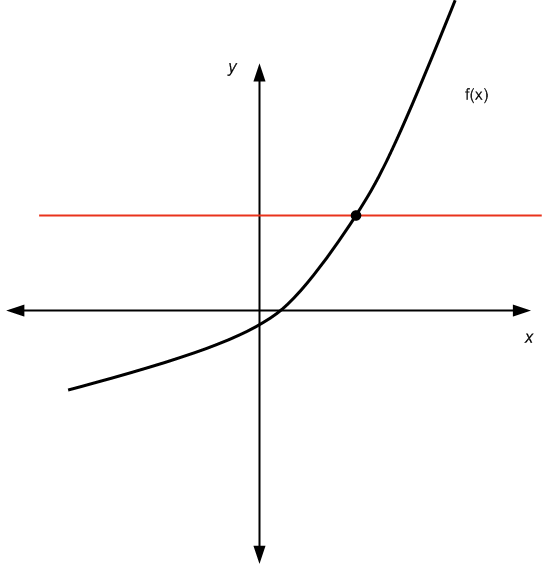
Для графического способа нам нужно использовать проверка горизонтальной линии : Для любой горизонтальной линии, которую мы рисуем, график функции не более одного раза пересекает эту горизонтальную линию.

Проходит тест горизонтальной линии

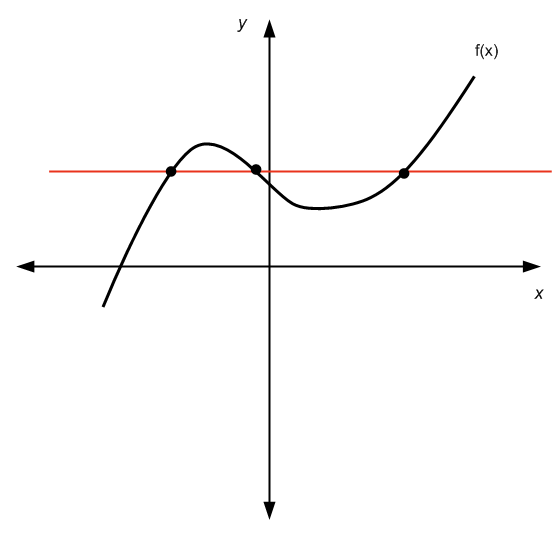
Не проходит тест горизонтальной линии

В поисках обратного

Чтобы найти обратную функцию для заданной функции \(f(x)\), необходимо решить уравнение.

Действительно, у вас есть уравнение \(f(x) = y\), вы берете \(y\) как заданное число, и вам нужно решить его для \(x\), и вам нужно убедиться, что решение УНИКАЛЬНО.

Это все. Легко, правда ??

Теперь о практических шагах:

Шаг 1: Для заданного \(y\) задайте уравнение:

и решите его для \(x\).

Шаг 2: Обязательно обратите внимание на то, для какого \(y\) существует действительно уникальное решение.

Шаг 3: Как только вы решите \(x\) в терминах \(y\), это выражение, которое зависит от \(y\), будет вашим \(f^<-1>(y)\).

Шаг 4: Измените имя переменной с \(y\) на \(x\), и у вас будет обратная функция \(f^<-1>(x)\).

ПРИМЕР 1

Найдите обратную функцию \(f(x) = \sqrt x\)

ОТВЕЧАТЬ:

Итак, мы берем \(y\) как данное, и нам нужно решить \(f(x) = y\), что в данном случае соответствует решению

Обратите внимание, что квадратный корень всегда неотрицателен, поэтому для решения нам понадобится \(y\ge 0\).

Применяя квадрат к обеим сторонам, получаем, что

\[\Rightarrow \,\, (\sqrt x)^2 = y^2\] \[\Rightarrow \,\, x = y^2\]

Итак, \(f^<-1>(y) = y^2\), переключая имя переменной, мы получаем обратную функцию:

ПРИМЕР 2

Найдите обратную функцию \(f(x) = \displaystyle \frac\) для \(x > -1\)

ОТВЕЧАТЬ:

Опять же, мы берем \(y\) как дано, и теперь нам нужно решить для \(x\) уравнение \(f(x) = y\). Итак, у нас есть

\[\displaystyle \frac = y\] \[\Rightarrow \,\, x = y(x+1)\] \[\Rightarrow \,\, x = yx + y\] \[\Rightarrow \,\, x — yx = y\] \[\Rightarrow \,\, x(1 — y) = y\] \[\Rightarrow \displaystyle \,\, x = \frac<1-y>\]

Итак, \(f^<-1>(y) = \displaystyle \frac<1-y>\), переключая имя переменной, мы получаем обратную функцию:

Подробнее о поиске обратной функции

Одним из важнейших свойств обратной функции \(f^<-1>(x)\) является то, что \(f(f^<-1>(x)) = x\).

Подумайте, о чем это говорит. Что-то вроде: «Функция, вычисленная в обратном порядке, дает вам идентичность».

Или, другими словами, вычисление инверсии через функцию похоже на бездействие с аргументом.

Или, как некоторые любят говорить: функция может каким-то образом отменить обратное.

Вы выбираете свою версию.

Как найти обратную квадратичную функцию? Ты можешь?

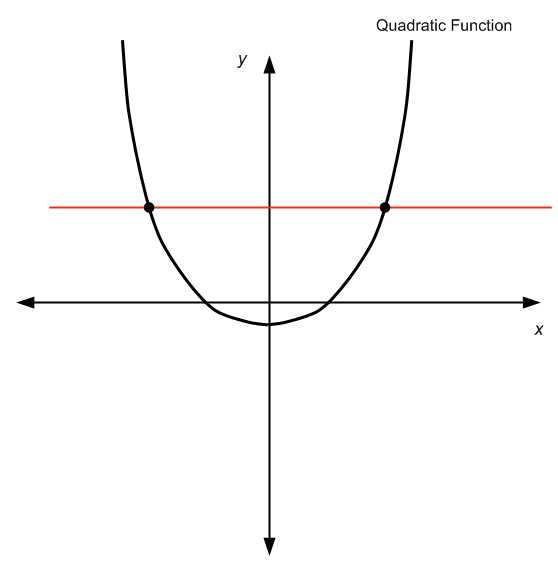
Собственно, ответ таков: это зависит от обстоятельств. Это потому, что если мы рассмотрим квадратичную функцию по всей реальной линии , то это не один к одному, поскольку он не проходит тест горизонтальной линии, как вы можете видеть на диаграмме ниже:

Не пройдя тест горизонтальной линии, мы можем увидеть, что для данного \(y\) существует более одного значения \(x\), так что \(f(x) = y\), поэтому мы не можем «решить» для \(x\), поскольку существует более одного \(x\).

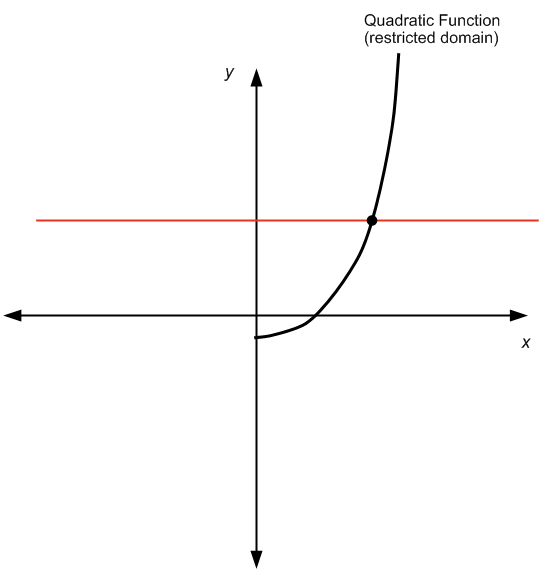
НО, если вы ограничите домен и рассмотрите, скажем, только положительные числа, мы получим следующее:

который проходит проверку горизонтальной линии, и, следовательно, квадратичная функция обратима.

НРАВСТВЕННОСТЬ ИСТОРИИ: Чтобы проверить, является ли что-то обратимым, речь идет НЕ только о функции. Речь идет о функции И ее домен и диапазон .

Как быстро построить график обратных функций

Всегда существует требование оценки, является ли функция \(f(x)\) обратимой или нет (проверяя, является ли она взаимно однозначной). Но если предположить, что вы знаете, что это обратимо, есть простой способ найти график обратимости.

Сначала изобразите график данной функции \(f(x)\).

Затем нарисуйте линию под углом 45 градусов \(y = x\).

Чтобы построить график \(f^<-1>(x)\), все, что вам нужно сделать, это отразить график \(f(x)\) через линию \(y = x\) под углом 45 градусов, как зеркало.

См. Пример ниже с функциями \(f(x) = \sin x\) и \(f^<-1>(x) = \arcsin x\).

Другой способ увидеть это — использовать оригинал график и измените значение \(x\) на значение \(y\).

Есть ли способ сделать функцию обратной?

Да, это действительно возможно, но это происходит только для функции идентификации, то есть с \(f(x) = x\).

Взаимно обратные функции, основные определения, свойства, графики

Понятие обратной функции

Допустим, что у нас есть некая функция y = f ( x ) , которая является строго монотонной (убывающей или возрастающей) и непрерывной на области определения x ∈ a ; b ; область ее значений y ∈ c ; d , а на интервале c ; d при этом у нас будет определена функция x = g ( y ) с областью значений a ; b . Вторая функция также будет непрерывной и строго монотонной. По отношению к y = f ( x ) она будет обратной функцией. То есть мы можем говорить об обратной функции x = g ( y ) тогда, когда y = f ( x ) на заданном интервале будет либо убывать, либо возрастать.

Две этих функции, f и g , будут взаимно обратными.

Для чего вообще нам нужно понятие обратных функций?

Это нужно нам для решения уравнений y = f ( x ) , которые записываются как раз с помощью этих выражений.

Нахождение взаимно обратных функций

Допустим, нам нужно найти решение уравнения cos ( x ) = 1 3 . Его решениями будут все точки: x = ± a rс c o s 1 3 + 2 π · k , k ∈ Z

Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.

Разберем несколько задач на нахождение функций, обратных заданным.

Условие: какая функция будет обратной для y = 3 x + 2 ?

Решение

Область определений и область значений функции, заданной в условии, – это множество всех действительных чисел. Попробуем решить данное уравнение через x , то есть выразив x через y .

Мы получим x = 1 3 y — 2 3 . Это и есть нужная нам обратная функция, но y здесь будет аргументом, а x — функцией. Переставим их, чтобы получить более привычную форму записи:

Ответ: функция y = 1 3 x — 2 3 будет обратной для y = 3 x + 2 .

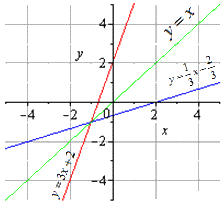
Обе взаимно обратные функции можно отобразить на графике следующим образом:

Мы видим симметричность обоих графиков относительно y = x . Эта прямая является биссектрисой первого и третьего квадрантов. Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.

Возьмем пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.

Условие: определите, какая функция будет обратной для y = 2 x .

Решение

Для заданной функции областью определения являются все действительные числа. Область значений лежит в интервале 0 ; + ∞ . Теперь нам нужно выразить x через y , то есть решить указанное уравнение через x . Мы получаем x = log 2 y . Переставим переменные и получим y = log 2 x .

В итоге у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.

Ответ: y = log 2 x .

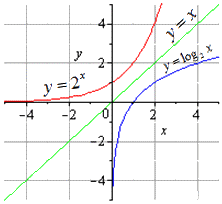
На графике обе функции будут выглядеть так:

Основные свойства взаимно обратных функций

В этом пункте мы перечислим основные свойства функций y = f ( x ) и x = g ( y ) , являющихся взаимно обратными.

1. Первое свойство мы уже вывели ранее: y = f ( g ( y ) ) и x = g ( f ( x ) ) .
2. Второе свойство вытекает из первого: область определения y = f ( x ) будет совпадать с областью значений обратной функции x = g ( y ) , и наоборот.
3. Графики функций, являющихся обратными, будут симметричными относительно y = x .
4. Если y = f ( x ) является возрастающей, то и x = g ( y ) будет возрастать, а если y = f ( x ) убывает, то убывает и x = g ( y ) .

Советуем внимательно отнестись к понятиям области определения и области значения функций и никогда их не путать. Допустим, что у нас есть две взаимно обратные функции y = f ( x ) = a x и x = g ( y ) = log a y . Согласно первому свойству, y = f ( g ( y ) ) = a log a y . Данное равенство будет верным только в случае положительных значений y , а для отрицательных логарифм не определен, поэтому не спешите записывать, что a log a y = y . Обязательно проверьте и добавьте, что это верно только при положительном y .

А вот равенство x = f ( g ( x ) ) = log a a x = x будет верным при любых действительных значениях x .

Не забывайте про этот момент, особенно если приходится работать с тригонометрическими и обратными тригонометрическими функциями. Так, a r c sin sin 7 π 3 ≠ 7 π 3 , потому что область значений арксинуса — π 2 ; π 2 и 7 π 3 в нее не входит. Верной будет запись

a r c sin sin 7 π 3 = a r c sin sin 2 π + π 3 = = п о ф о р м у л е п р и в и д е н и я = a r c sin sin π 3 = π 3

А вот sin a r c sin 1 3 = 1 3 – верное равенство, т.е. sin ( a r c sin x ) = x при x ∈ — 1 ; 1 и a r c sin ( sin x ) = x при x ∈ — π 2 ; π 2 . Всегда будьте внимательны с областью значений и областью определений обратных функций!

Графики взаимно обратных функций

• Основные взаимно обратные функции: степенные

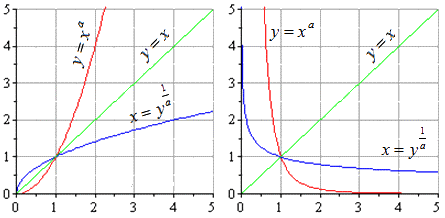
Если у нас есть степенная функция y = x a , то при x > 0 степенная функция x = y 1 a также будет обратной ей. Заменим буквы и получим соответственно y = x a и x = y 1 a .

На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):

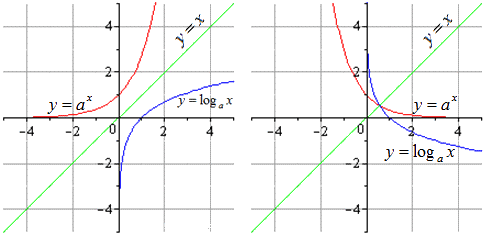
• Основные взаимно обратные функции: показательные и логарифмические

Возьмем a,которое будет положительным числом, не равным 1 .

Графики для функций с a > 1 и a 1 будут выглядеть так:

• Основные взаимно обратные функции: тригонометрические и обратные тригонометрические

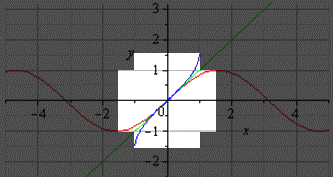
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):

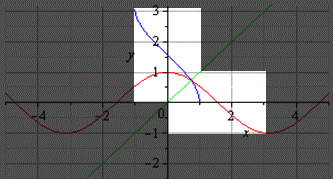
График главной ветви косинуса и арккосинуса выглядит так:

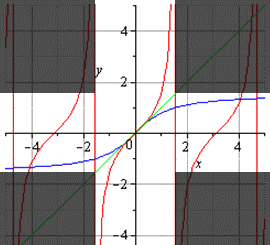
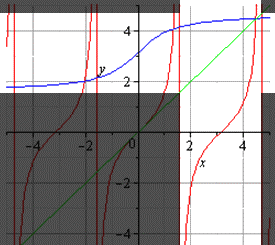
График главной ветви арктангенса и тангенса:

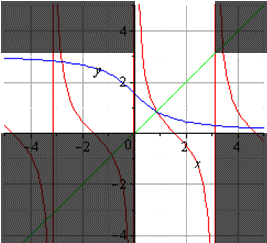
График главной ветви арккотангенса и котангенса будет таким:

Если же вам требуется построить обратные ветви, отличные от главных, то обратную тригонометрическую функцию при этом мы сдвигаем вдоль оси O y на нужное число периодов. Так, если требуется обратная функция для ветви тангенса на π 2 ; 3 π 2 , то мы можем сдвинуть ее на величину π вдоль оси абсцисс. График будет представлять собой ветвь арктангенса, которая сдвинута на π вдоль оси ординат.

Это все свойства обратных функций, о которых мы хотели бы вам рассказать.