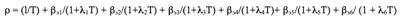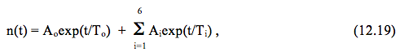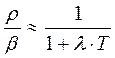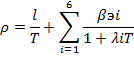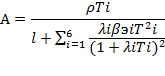Уравнение обратных часов в ядерной физике

12.1.4. Уравнение обратных часов.

а ) Уравнение обратных часов как характеристическое уравнение системы дифференциальных уравнений кинетики реактора. Развёрнутый вид уравнения обратных часов:

свидетельствует о том, что это — алгебраическое уравнение седьмой степени относительно Т. Для того, чтобы понять это, достаточно мысленно представить, что получится в числителе выражения правой части уравнения после приведения его к общему знаменателю: седьмая степень уравнения становится очевидной. А это значит, что уравнение обратных часов в самом общем случае должно иметь семь корней.

В разделе математики “Решение дифференциальных уравнений” говорится, что вид, величины и знаки корней характеристического уравнения определяют вид решения дифференциальных уравнений. В частности, если характеристическое уравнение имеет действительные корни, то решение дифференциального уравнения (или системы дифференциальных уравнений) имеет экспоненциальный вид. Это побуждает нас заняться анализом корней уравнения обратных часов.

Но вначале следует уточнить одну немаловажную деталь: отыскивая с самого начала именно экспоненциальное решение для дифференциального уравнения изменения плотности нейтронов в виде одной экспоненты — n(t) = n_o exp (t / T), — мы невольно совершили небольшой просчёт, который следует исправить по ходу дела. Если уравнение обратных часов имеет семь корней, то общее решение системы дифференциальных уравнений кинетики реактора будет не одной экспонентой, а будет представлять собой сумму семи экспонент, показатели которых определяются величинами этих семи корней уравнения обратных часов:

или в более краткой форме:

где Т_о, T₁, T₂, . , T₆ — значения семи корней уравнения обратных часов, а A_o, A₁, A₂, . , A₆ — величины постоянных интегрирования, находимые путём подстановки в общее решение (12.19) конкретных начальных условий.
Знаки корней уравнения обратных часов наиболее наглядно видны, если показать его решение в графическом виде (см. рис.12.3).

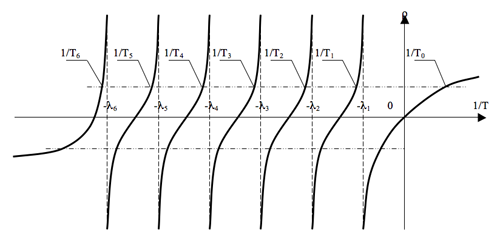
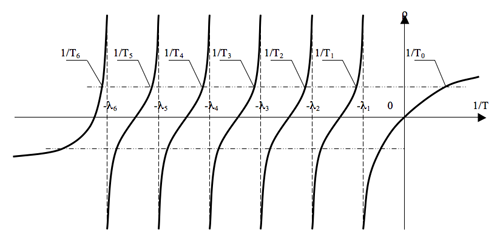
Рис. 12.3. График зависимости корней уравнения обратных часов при положительных и отрицательных реактивностях разной величины.

На этом графике показано решение уравнения обратных часов в зависимости не от величины самого периода Т, а от обратной ему величины 1/Т: так удобнее выполнять решение уравнения аналитически.
Как видим, функция ρ = f (1/T) имеет шесть точек разрыва (второго рода), и именно благодаря этой разрывности отдельные корни уравнения обратных часов отображаются на графике достаточно наглядно: области изменения каждого из семи корней по оси 1/T лежат между соответствующими точками разрыва; например, нулевой обратный корень 1/Т_о лежит правее первой точки разрыва (- λ₁), первый обратный корень 1/Т₁ — между первой и второй точками разрыва (—λ₁ и —λ₂), второй обратный корень 1/T₂ — между второй и третьей точками разрыва (—λ₂ и —λ₃ ) и так далее; значения последнего, седьмого, обратного корня 1/Т₇ — располагаются левее последней, шестой, точки разрыва (—λ₆).

При этом знаки всех семи корней уравнения обратных часов определяются самым наглядным образом: в точках пересечения соответствующих участков графика с горизонтальной прямой, отсекающей на оси ординат рассматриваемое значение реактивности ρ.

Из графика видно, что, если величина сообщаемой реактору реактивности положительна, то нулевой обратный корень 1/Т_о , а, значит, и сам корень Т_о, — положителен (т.к. располагается в правой полуплоскости, правее оси О — ρ). Остальные шесть корней (Т₁ ÷ Т₆) уравнения обратных часов — отрицательны (лежат в левой полуплоскости). Если же величина сообщаемой реактору реактивности отрицательна, то все семь корней уравнения обратных часов отрицательны (лежат в левой, отрицательной, полуплоскости).Что касается величин самих корней, то они, как следует из графика, определяются только величиной сообщаемой реактору реактивности ρ.
Теперь о знаках постоянных интегрирования (А_о ÷ А₆). Здесь не приводится полный (и очень громоздкий) аналитический вывод общего выражения для любой из постоянных интегрирования, которое имеет вид:

Квадрат выражения в скобках под знаком суммы, независимо от знака корня Т_i , всегда имеет положительный знак, и, поскольку все остальные величины знаменателя положительны, то весь знаменатель (12.20) — всегда положителен. А раз так, то знак постоянной интегрирования А_i всегда определяется знаком произведения ρТ_i в числителе правой части этого выражения. То есть, если нулевой корень Т_о при ρ > 0, как говорилось выше, положителен (Т_о > 0), то произведение ρ Т_о > 0, а, следовательно, А_о > 0. При отрицательной же величине реактивности (ρ ρ даёт положительную величину произведения ρ Т_о, и, следовательно, величина нулевой постоянной интегрирования будет иметь положительный знак. Проделав такой микроанализ со всеми величинами постоянных интегрирования, можно прийти к общему выводу:
при ρ >0: Т_о > 0 и А_о > 0, а остальные корни (Т₁÷Т₆) ÷А₆) ρ ÷Т₆) ÷А₆)>0 (12.22)

б) Самостоятельное практическое значение решения уравнения обратных часов.
Анализ знаков корней уравнения обратных часов и постоянных интегрирования безусловно важен, так как он даёт возможность выявить качественную структуру и дать физическое толкование характеру переходных процессов при сообщении реактору реактивности того или иного знака.
Но значение уравнения обратных часов не исчерпывается только этим. Забегая немного вперёд, заметим, что из семи корней уравнения обратных часов старший корень Т_о (старший — в математическом понимании этого слова, то есть — наибольший по величине) имеет простое физическое толкование: это — тот самый установившийся период, определяющий “чисто экспоненциальное” изменение плотности нейтронов в реакторе в развитой стадии переходного процесса n(t). (Почему это так, станет ясно немного позже).
Эту величину установившегося периода, как уже говорилось, легко измерить практически с помощью самого обычного секундомера. Вместе с тем, величина установившегося периода (Т_о) для конкретного реактора в рассматриваемый момент кампании определяется только величиной сообщённой реактору реактивности ρ, следовательно, уравнение обратных часов для конкретного реактора (с конкретной величиной β_э) устанавливает жёсткую однозначную взаимосвязь величин реактивности ρ и установившегося периода Т_о (или ρ — с величиной установившегося периода удвоения мощности реактора Т₂, которая, как мы знаем, пропорциональна величине установившегося периода Т_о).
А это значит, что по величине измеренного установившегося периода удвоения мощности можно находить величину сообщённой реактору реактивности, и, наоборот, — по величине сообщённой реактору реактивности можно предсказывать, с каким установившимся периодом удвоения будет происходить установившийся разгон (или спад) мощности ядерного реактора. Это, согласитесь, практически очень важно для оператора реакторной установки. Эту взаимосвязь можно занести в программу компьютера, можно выразить в форме таблицы или в форме графика.

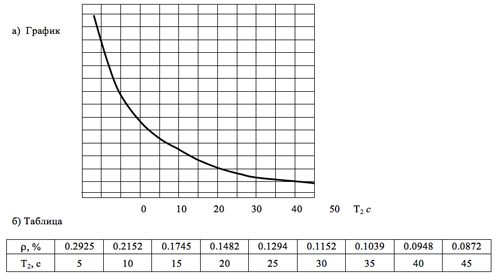
Рис. 12.2. Две наглядные формы взаимосвязи реактивности реактора ρ и установившегося периода удвоения мощности реактора Т₂ , вытекающие из решения уравнения обратных часов.

Пользуясь приведенными таблицей или графиком, оператор имеет возможность быстро оценить величину реактивности реактора по измеренному периоду удвоения мощности или предсказать величину установившегося периода разгона реактора по величине реактивности, которую он собирается сообщить реактору.

Реактивность. Связь реактивности с периодом. Уравнение обратных часов.

Протекание цепного ядерного процесса характеризуется эффективным коэффициентом размножения нейтронов в реакторе K_eff. Реактивность — относительное отклонение К_eff от 1. ρ = (К_eff – 1)/K_eff. В случае, если реактивность равна нулю, реактор находится в критическом состоянии, т.е. число нейтронов остаётся постоянным во времени. При положительной реактивности начинается разгон реактора – число нейтронов в каждом последующем поколении превышает число нейтронов в текущем.

Период реактора — время, в течение которого плотность потока нейтронов, а следовательно и плотность нейтронов возрастает в e раз.

Время жизни поколения нейтронов:

l = время деления + время замедления + время диффузии

определяющим является время диффузии

Связь реактивности с периодом реактора определяется через формулу обратных часов:

ρ – реактивность

β – доля запаздывающих нейтронов

λ – одногрупповая постоянная распада предшественников запаздывающих нейтронов

T – период

Дата добавления: 2015-05-30 ; просмотров: 4774 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Уравнение Нордхейма (обратных часов) и его решение

— уравнение обратных часов (УОЧ) или уравнение Нордхейма. Первое слагаемое определяет влияние мгновенных нейтронов, второе – запаздывающих.

Уравнение обратных часов имеет семь корней, тогда общее решение системы дифференциальных уравнений кинетики реактора будет не одной экспонентой, а будет представлять собой сумму семи экспонент, показатели которых определяются величинами этих семи корней уравнения обратных часов:

или в краткой форме:

,

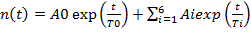
где Т_о, T₁, T₂, . , T₆ — значения семи корней уравнения обратных часов, а A_o, A₁, A₂, . , A₆ — величины постоянных интегрирования, находимые путём подстановки в общее решение конкретных начальных условий.
Знаки корней уравнения обратных часов наиболее наглядно видны, если показать его решение в графическом виде:

Рис. График зависимости корней уравнения обратных часов при положительных и отрицательных реактивностях разной величины.

На этом графике показано решение уравнения обратных часов в зависимости не от величины самого периода Т, а от обратной ему величины 1/Т: так удобнее выполнять решение уравнения аналитически.
Как видим, функция ρ = f (1/T) имеет шесть точек разрыва (второго рода), и именно благодаря этой разрывности отдельные корни уравнения обратных часов отображаются на графике достаточно наглядно: области изменения каждого из семи корней по оси 1/T лежат между соответствующими точками разрыва; например, нулевой обратный корень 1/Т_о лежит правее первой точки разрыва (- λ₁), первый обратный корень 1/Т₁ — между первой и второй точками разрыва (-λ₁и-λ₂), второй обратный корень 1/T₂ — между второй и третьей точками разрыва (-λ₂и-λ₃ ) и так далее; значения последнего, седьмого, обратного корня 1/Т₇ — располагаются левее последней, шестой, точки разрыва (-λ₆).
При этом знаки всех семи корней уравнения обратных часов определяются самым наглядным образом: в точках пересечения соответствующих участков графика с горизонтальной прямой, отсекающей на оси ординат рассматриваемое значение реактивности ρ.
Из графика видно, что, если величина сообщаемой реактору реактивности положительна, то нулевой обратный корень 1/Т_о , а, значит, и сам корень Т_о, — положителен (т.к. располагается в правой полуплоскости, правее оси О — ρ). Остальные шесть корней (Т₁ ÷ Т₆) уравнения обратных часов — отрицательны (лежат в левой полуплоскости). Если же величина сообщаемой реактору реактивности отрицательна, то все семь корней уравнения обратных часов отрицательны (лежат в левой, отрицательной, полуплоскости).Что касается величин самих корней, то они, как следует из графика, определяются только величиной сообщаемой реактору реактивности ρ.
Теперь о знаках постоянных интегрирования (А_о ÷ А₆). Здесь не приводится полный (и очень громоздкий) аналитический вывод общего выражения для любой из постоянных интегрирования, которое имеет вид:

Квадрат выражения в скобках под знаком суммы, независимо от знака корня Т_i, всегда имеет положительный знак, и, поскольку все остальные величины знаменателя положительны, то весь знаменатель — всегда положителен. А раз так, то знак постоянной интегрирования А_i всегда определяется знаком произведения ρТ_i в числителе правой части этого выражения. То есть, если нулевой корень Т_о при ρ > 0, как говорилось выше, положителен (Т_о>0), то произведение ρТ_о > 0, а, следовательно, А_о > 0. При отрицательной же величине реактивности (ρ 0: Т_о>0 и А_о>0, а остальные корни (Т₁÷Т₆) 0.

Дата добавления: 2021-05-28 ; просмотров: 180 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ