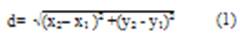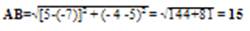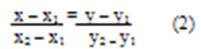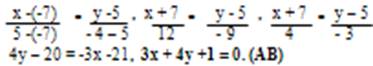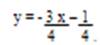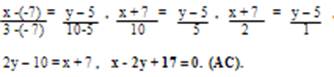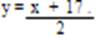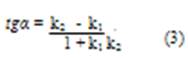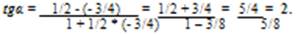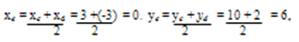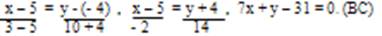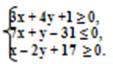Уравнение окружности которой высота cd есть диаметр

Определение объема и площади геометрических фигур. Системы линейных неравенств

Размещено на http:///

57. даны вершины треугольника АВС. Найти

1) длину стороны АВ;

2) уравнения сторон АВ и АС и их угловые коэффициенты;

3) внутренний угол А;

4) уравнение медианы проведенной ихз вершины В;

5) уравнение высоты СD и ее длину;

6)уравнение окружности для которой высота СD есть диаметр и точки пересечения этой окружности со стороной АС;

7) уравнение биссектрисы внутреннего угла А;

8) площадь треугольника АВС;

9) систему линейных неравенств, определяющих треугольник АВС.

= = 15 — длина стороны АВ

Уравнение прямой, проходящей через точки

Подставим координаты точек А и В в это уравнение прямой

S_AB = (- 3, — 4) называется направляющим вектором прямой АВ. Этот вектор параллелен прямой АВ.

— 4х + 28 = — 3у + 27

— 4х + 3у + 1 = 0 — уравнение прямой АВ

Если уравнение записать в виде: у = х — то можно выделить его угловой коэффициент: k₁ =4/3

Вектор N_AB = (-4, 3) называется нормальным вектором прямой AB.

Вектор N _AB = (-4, 3) перпендикулярен прямой AB.

Аналогично найдем уравнение стороны АС

S_AС = (- 7, — 1) — направляющий вектор стороны АС

— х + 7у — 56 = 0 — уравнение стороны АС

у = = х + 8 откуда угловой коэффициент k₂ = 1/7

Вектор N _AC = (- 1, 7) — нормальный вектор прямой AC.

Вектор N _AC = (- 1, 7) перпендикулярен прямой AC.

Запишем формулу скалярного произведения векторов и

Для нахождения угла А достаточно найти косинус данного угла. Из предыдущей формулы запишем выражение для косинуса угла А

Находим скалярное произведение векторов и

Длина вектора = 15 (нашли ранее)

Найдем длину вектора

= = 14,14 — длина стороны АС

Тогда cos LA = = 0,7072

Уравнение медианы в общем виде

Теперь необходимо найти направляющий вектор прямой ВЕ.

Достроим треугольник АВС до параллелограмма АВСD, таким образом, чтобы сторона АС являлась его диагональю. Диагонали в параллелограмме делятся пополам, т. е. АЕ = ЕС. Следовательно, точка E лежит на прямой BF.

В качестве направляющего вектора прямой BE можно принять вектор , который и найдем .

= + = (-5 + 9; 10 + 12) = (4; 22)

Подставим в уравнение

Подставим координаты точки С (-7; 7)

11х + 77 = 2у — 14

11х — 2у + 91 = 0 — уравнение медианы ВЕ

Так как точка Е — середина стороны АС, то ее координаты

Координаты точки Е (0; 8)

Уравнение в общем виде

Необходимо найти направляющий вектор прямой СD

Прямая СD перпендикулярна прямой АВ, следовательно, направляющий вектор прямой СD параллелен нормальному вектору прямой АВ

То есть в качестве направляющего вектора прямой CD можно принять нормальный вектор прямой АВ

Вектор _AB найден ранее: _AB (-4, 3)

Подставим координаты точки С, (- 7; 7)

3х + 21 = — 4у + 28

3х + 4у — 7 = 0 — уравнение высоты С D

Координаты точки D:

Точка D принадлежит прямой АВ, следовательно, координаты точки D(x_d. y_d) должны удовлетворять уравнению прямой АВ, найденному ранее

Точка D принадлежит прямой CD, следовательно, координаты точки D(x_d. y_d) должны удовлетворять уравнению прямой CD,

Составим систему уравнений на основе этого

Координаты D(1; 1)

Найдем длину прямой CD

= = 10 — длина прямой СD

Очевидно, что прямая СD проходит через начало координат так как ее уравнение -3х — 4у = 0, следовательно, уравнение окружности можно записать в виде

(х — а ) 2 + (у — b) 2 = R 2 — уравнение окружности с центром в точке (а; b)

Здесь R = СD/2 = 10 /2 = 5

(х — а ) 2 + (у — b ) 2 = 25

Центр окружности О (а; b) лежит на середине отрезка СD. Найдем его координаты:

(х + 3) 2 + (у — 4) 2 = 25

Найдем пересечение этой окружности со стороной АС:

точка К принадлежит одновременно окружности и прямой АС

— х + 7у — 56 = 0 — уравнение прямой АС, найденной ранее.

Таким образом, получили квадратное уравнение

50у 2 — 750у +2800 = 0

у 2 — 15у + 56 = 0

у₂ = 7 — точка, соответствующая точке С

следовательно координаты точки Н:

Воспользуемся свойством биссектрисы треугольника:

Биссектриса делит противоположную сторону на части, пропорционально прилежащим к ней сторонам:

Если точка Н(x_h y_h) лежит на прямой, проходящей через две точки В(х₁, у₁) = (-2, -3) и С(х₂, у₂) = (-7, 7) И дано отношение г , в котором точка Н делит отрезок ВС, то координаты точки Н определяются как

Системы линейных неравенств
Существование и способ построения фундаментального набора решений для систем, состоящих из одного или нескольких неравенств. Метод последовательного у.

Определение площади геометрической фигуры
Вычисление площади геометрических фигур с помощью интегрального исчисления. Основные свойства площади как функции. Разработка алгоритма работы програм.

Моделирование системы геометрических фигур
Объектно-ориентированные возможности языка C++. Моделирование системы геометрических фигур, методика проектирования программных комплексов. Анализ пре.

Алгоритмизация и программирование
Рассмотрение способов построения алгоритмов для решения конкретных задач. Программирование с помощью базовых операторов языка Turbo Pascal. Решение за.

Геометрические приложения определенного интеграла
Вычисление площадей плоских фигур. Нахождение определенного интеграла функции. Определение площади под кривой, площади фигуры, заключенной между кривы.

Дифференциальные уравнения

Даны вершины треугольника АВС.

Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты CD и ее длину; 5) уравнение окружности, для которой высота CD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС.

Подставив в эту формулу координаты точек А и В имеем:

Подставив в формулу (2) координаты точек А и В, получим уравнение прямой АВ:

Для нахождения углового коэффициента k_ab прямой АВ разрешим полученное уравнение относительно у:

Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС.

Для нахождения углового коэффициента k_aс прямой АС разрешим полученное уравнение относительно у:

3. Угол α между двумя прямыми, угловые коэффициенты которых равны k₁ и k₂, определяется по формуле:

Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее

2 + (2 -10) 2 = √36 + 64 = 10 .

5. Уравнение окружности радиуса R с центром в точке E(a;b) имеет вид:

(х – а) 2 + (у – b) 2 = R 2 (5)

Так как СD является диаметром искомой окружности, то ее центр Е есть середина отрезка CD. Воспользовавшись формулами деления отрезка пополам, получим:

Следовательно E(0;6) и R = CD/2 = 5. Используя формулу (5), получим уравнение искомой окружности:

(х – 0) 2 + (у – 6) 2 = 25, х 2 + (у – 6) 2 = 25.

6. Множество точек треугольника АВС есть пересечение трех полуплоскостей, первая из которых ограничена прямой АВ и содержит точку С, вторая прямая ВС и содержит точку А, а третья ограничена прямой АС и содержит точку В. Для получения неравенства, определяющего полуплоскость, ограниченную прямой АВ и содержащую точку С, подставим в уравнение прямой АВ координаты точки С:

3* 3+ 4*10 +1 = 50 > 0.

поэтому искомое неравенство имеет вид:

Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВС и содержащую точку А, найдем уравнение прямой ВС, подставив в формулу (2) координаты точек В и С:

Подставив в последнее уравнение координаты точки А, имеем:

7* (- 7) + 5 – 31 = — 75 0.

Третье искомое неравенство

Итак, множество точек треугольника АВС определяется системой неравенств:

Даны векторы a₁ , a₂ , a₃ , b . Показать, что векторы a₁ , a₂ , a₃ образуют базис трехмерного пространства и найти координаты вектора b в этом базисе.

1. Система векторов 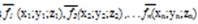в пространстве R n линейно независима тогда и только тогда, когда отличен от нуля определитель, строками (столбцами) которого являются координаты векторов системы:

Подставив в формулу (1) координаты векторов a₁ , a₂ , a₃ найдем определитель:

Так как определитель не равен нулю, то данные три вектора являются линейно независимыми. Соответственно они образуют базис трехмерного пространства.

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):