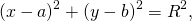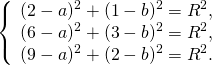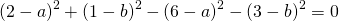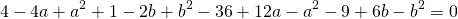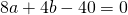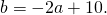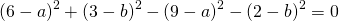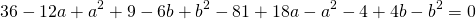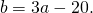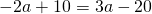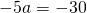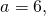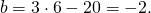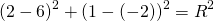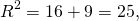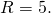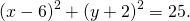Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Уравнение окружности описанной вокруг треугольника
Уравнение окружности, описанной около треугольника
Составить уравнение окружности, описанной около треугольника, стороны которого заданы уравнениями \(9x-2y-41=0\), \(7x+4y+7=0\), \(x-3y+1=0\).
Найдем координаты вершин треугольника, решив совместно три системы уравнений: $$ \cases < 9x-2y-41=0, \cr 7x+4y+7=0; >\cases < 9x-2y-41=0, \cr x-3y+1=0; >\cases < 7x+4y+7=0, \cr x-3y+1=0; >$$ В результате получим \(A(3;-7),B(5;2),C(-1;0).\) Пусть искомое уравнение окружности имеет вид \((x-a)^2+(y-b)^2=r^2\). Для нахождения \(a\), \(b\) и \(r\) напишем три равенства, подставив в искомое уравнение вместо текущих координат координаты точек \(A\), \(B\) и \(C\): $$(3-a)^2+(-7-b)^2=r^2; (5-a)^2+(2-b)^2=r^2; (-1-a)^2+b^2=r^2.$$ Исключая \(r^2\), приходим к системе уравнений $$\cases < (3-a)^2+(-7-b)^2=(5-a)^2+(2-b)^2, \cr (3-a)^2+(-7-b)^2=(-1-a)^2+b^2, >$$ или $$\cases < 4a+18b=-29, \cr 8a-14b=57. >$$ Отсюда \(a=3.1\), \(b=2.3\). Значение \(r^2\) находим из уравнения \((-1-a)^2+b^2=r^2\), т.е. \(r^2=22.1\). Итак, искомое уравнение записывается в виде \((x-3.1)^2+(y+2.3)^2=22.1\).
Окружность, описанная около треугольника
Определение и формулы круга, описываемого вокруг треугольника
Круг, проходящий через все три вершины треугольника, называется его описанной окружностью.
Центр описанной окружности лежит на пересечении средних перпендикуляров к сторонам треугольника.
Круг может быть описан вокруг любого треугольника и только одного.
Радиус \(\ \mathrm
Радиус круга, описанного вокруг треугольника, равен отношению стороны треугольника к двойному синусу противоположного угла (следствие теоремы синуса):
В правом треугольнике центр описанной окружности лежит в середине гипотенузы.
Примеры решения проблем
Найти радиус окружности, описанной около треугольника \(\ \mathrm
Радиус \(\ R \) окружности, описываемой вокруг треугольника, найден из уравнения
Сумма углов произвольного треугольника равна \(\ 180^ <\circ>\) , поэтому
Теперь вы можете найти радиус окружности:
В треугольнике \(\ \mathrm
Радиус описанной окружности равен отношению стороны треугольника к двойному синусу противоположного угла
Из письменных равенств находим синусы углов B и C треугольника:
\(\ \sin \angle C=\frac<2 R>=\frac<8><8>=1, \sin \angle B=\frac<2 R>=\frac<6><8>=\frac<1> <2>\) откуда следует, что \(\ \angle C=90^ <\circ>\) и \(\ \angle B=30^ <\circ>\)
http://primat.org/publ/reshennye_zadachi/uravnenie_okruzhnosti_opisannoj_okolo_treugolnika/43-1-0-597
http://www.homework.ru/spravochnik/okruzhnost-opisannaya-okolo-treugolnika/