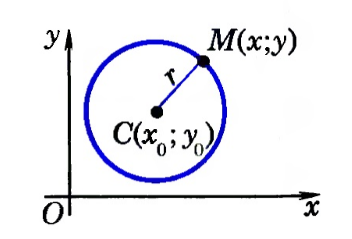Уравнение окружности прямой проходящей через точку

Уравнение окружности и прямой

Вы будете перенаправлены на Автор24

Уравнение линии на плоскости

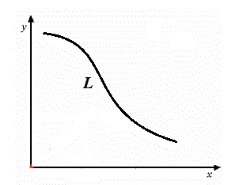
Введем для начала понятие уравнения линии в двумерной системе координат. Пусть в декартовой системе координат построена произвольная линия $L$ (Рис. 1).

Рисунок 1. Произвольная линия в системе координат

Уравнение с двумя переменными $x$ и $y$ называется уравнением линии $L$, если этому уравнению удовлетворяют координаты любой точки, принадлежащей линии $L$ и не удовлетворяет ни одна точка, не принадлежащая линии $L.$

Уравнение окружности

Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).

Рисунок 2. Окружность в декартовой системе координат

Расстояние от центра окружности до точки $M$ вычисляется следующим образом

Но, так как $M$ лежит на окружности, то получаем $CM=r$. Тогда получим следующее

Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.

В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид

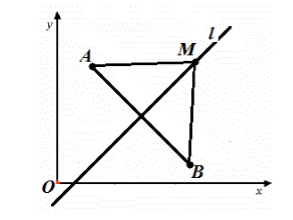
Выведем уравнение прямой $l$ в декартовой системе координат $xOy$. Пусть точки $A$ и $B$ имеют координаты $\left\$ и $\$ соответственно, причем точки $A$ и $B$ выбраны так, что прямая $l$ — серединный перпендикуляр к отрезку $AB$. Выберем произвольную точку $M=\$, принадлежащую прямой $l$ (рис. 3).

Готовые работы на аналогичную тему

Рисунок 3. Прямая в декартовой системе координат

Так как прямая $l$ — серединный перпендикуляр к отрезку $AB$, то точка $M$ равноудалена от концов этого отрезка, то есть $AM=BM$.

Найдем длины данных сторон по формуле расстояния между точками:

Обозначим через $a=2\left(x_1-x_2\right),\ b=2\left(y_1-y_2\right),\ c=^2+^2-^2-^2$, Получаем, что уравнение прямой в декартовой системе координат имеет следующий вид:

Здесь можно выделить два частных случая для уравнения прямой. Пусть прямая $l$ проходит через точку $M=\$, тогда

Если прямая $l$ параллельна оси $Ox$, то она имеет вид

Если прямая $l$ параллельна оси $Oy$, то она имеет вид

Пример задачи на нахождение уравнений линий в декартовой системе координат

Найти уравнение окружности с центром в точке $(2,\ 4)$. Проходящей через начало координат и прямую, параллельную оси $Ox,$ проходящей через её центр.

Решение.

Найдем сначала уравнение данной окружности. Для этого будем использовать общее уравнение окружности (выведенное выше). Так как центр окружности лежит в точке $(2,\ 4)$, получим

Найдем радиус окружности как расстояние от точки $(2,\ 4)$ до точки $(0,0)$

Получаем, уравнение окружности имеет вид:

Найдем теперь уравнение окружности, используя частный случай 1. Получим

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 05 04 2021

Решение задач по темам «Уравнение окружности» и «Уравнение прямой»

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На прошлых уроках мы вывели уравнение окружности и решили некоторые задачи на уравнение окружности, вывели уравнение прямой и решили соответствующие задачи. На этом уроке мы продолжим решение задач на уравнение окружности и уравнение прямой.

Уравнение окружности, уравнение прямой

Уравнение окружности с радиусом R и с центром в точке O \(( x_0;y_0)\) имеет вид: \(( x-x_0 )^2 + ( y-y_0)^2 = R^2 \) .

Если центр окружности совпадает с началом координат, то уравнение окружности упрощается: \(x^2+y^2=R^2\) .

Пример 1. Дано урав­не­ние окруж­но­сти: \((x-1)^2+(y+2)^2=4\) . Найдем центр и ра­ди­ус.

Ре­ше­ние: Центр этой окруж­но­сти – точка \(C(1;-2)\) , ра­ди­ус \(R=2\) .

Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида \(Ax + By + C = 0\) , где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при \(b≠0\) можно привести к виду:

\(y = kx + b\) , где \(k\) – угловой коэффициент, равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.

Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами \((a; 0)\ и\ (0; b)\) , то она может быть найдена, используя формулу уравнения прямой в отрезках: \(\frac+\frac=1\) .

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки \(A(x_1;y_1)\) и \(B(x_2; y_2)\) , такие, что \(x_1 ≠ x_2\ и\ y_1 ≠ y_2\) , то уравнение прямой можно найти, используя следующую формулу: \(\frac=\frac\) .

Пример 2. Составим общее уравнение прямой, которая в прямоугольной системе координат проходит через две точки \(M_1(1;1)\) и \(M_2(4;2)\) .

Решение: Сначала напишем уравнение прямой, проходящей через две заданные точки. Оно имеет вид \(\frac<4-1>=\frac <2-1>\Leftrightarrow \frac3=\frac1\) . Теперь приведем полученное уравнение к требуемому виду: \(\frac3=\frac1 \Leftrightarrow 1\cdot (x-1)=3\cdot(y-1) \Leftrightarrow x-3y+2=0\) .

Составьте уравнение прямой, содержащей медиану \(MK\) треугольника \(MDC\) , если его вершины – \(M(- 1; 5), D(8; — 2), C(- 4; — 2)\) .

Найдите координаты точек пересечения окружности \(x^2+y^2 — 8x- 8y + 7 = 0\) с осью абсцисс.