Уравнение окружности сферы плоскости презентация

Уравнения сферы, плоскости и прямой
презентация к уроку по геометрии (10, 11 класс)

Уравнения сферы, плоскости и прямой

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Понятие сферы и её элементов Уравнение сферы в заданной системе координат СФЕРА УРАВНЕНИЕ СФЕРЫ

Тело вращения — сфера

Определение сферы Элементы сферы Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. т.О — центр сферы ОА – радиус сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы называется радиусом сферы. ВС – диаметр сферы. Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы d=2r

? Какие из тел, изображенных на рисунках, являются сферой? 1 2 3 4 5 6

На плоскости В пространстве L М(х;у) х у L Сформулируйте определение линии L на плоскости Уравнение с двумя переменными х и у называется уравнением линии L , если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии Уравнение с тремя переменными х,у, z называется уравнением поверхности, если этому уравнению удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности Х z Сформулируйте определение уравнения поверхности в пространстве Х у М(х;у; z ) •

На плоскости В пространстве М(х;у) х у х у z (х;у; z ) С

Частные случаи 1.Уравнение окружности с центром в т.О(0;0) и радиусом r 1.Уравнение сферы с центром в т.О(0;0;0) и радиусом R

Выбрать из предложенных уравнений – уравнение сферы: 1. 2. 3. 4. 5. 6. 7. 8. 1.Ур-е окружности 2.Ур-е сферы 3.Ур-е прямой 4.Ур-е сферы 5.Ур-е параболы 6.Ур-е сферы 7.Ур-е сферы 8. ?

В данных уравнениях определите координаты центра сферы и радиус 1. 2. 3. 4.

Составьте уравнение сферы по следующим данным центра и радиуса сферы: Дано: С(-2;8;1); R =11 Дано: А(3;-2;0); R =0,7 Дано: О(0;0;0); R =1 Проверяем ответы:

Задача Определить принадлежит ли т.А сфере, заданной уравнением если: а) т.А(5;-2;6) б) т.А(-5;2;6) Решение: Равенство верное , следовательно А(5;-2;6) принадлежит сфере Равенство неверное , следовательно А(5;-2;6) не принадлежит сфере

Уравнение плоскости и прямой

совпадают, если существует такое число k , что параллельны, если существует такое число k , что В остальных случаях плоскости пересекаются.

Если известна какая-нибудь точка плоскости M 0 и какой-нибудь вектор нормали к ней , то через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору. Общее уравнение плоскости будет иметь вид: n (A;B;C) M 0

Чтобы получить уравнение плоскости , имеющее приведённый вид, возьмём на плоскости произвольную точку M( x ; y ; z ) . Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис), а для этого, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е. Вектор задан по условию. Координаты вектора найдём по формуле : Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:

Используем формулу A ( x — x 0 )+B(y-y 0 )+C(z-z 0 )=0

Уравнение прямой в пространстве Поскольку прямую в пространстве можно рассматривать как линию пересечения двух плоскостей, то одним из способов аналитического задания прямой в пространстве является задание с помощью системы из двух уравнений задающих пару пересекающихся плоскостей.

Уравнение прямой в пространстве Прямую, проходящую через точку A 0 ( x 0 , y 0 , z 0 ) с направляющим вектором ( a , b , c ) можно задавать параметрическими уравнениями В случае, если прямая в пространстве задается двумя точками A 1 ( x 1 , y 1 , z 1 ), A 2 ( x 2 , y 2 , z 2 ), то, выбирая в качестве направляющего векто­ра вектор ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) и в качестве точки А 0 точку А 1 , получим следующие уравнения

Упражнение 1 Какими уравнениями задаются координатные прямые? Ответ: Ось Ox Ось O y Ось O z

Упражнение 2 Напишите параметрические уравнения прямой, проходящей через точку А (1,-2,3) с направляющим вектором, имеющим координаты (2,3,-1). Ответ:

Упражнение 3 Напишите параметрические уравнения прямой, проходящей через точки А 1 (-2,1,-3), А 2 (5,4,6). Ответ:

Упражнение 4 Напишите параметрические уравнения прямой, проходящей через точку M (1,2,-3) и перпендикулярную плоскости x + y + z + 1 = 0. Ответ:

Упражнение 5 В каком случае параметрические уравнения определяют перпендикулярные прямые? Ответ: Если выполняется равенство a 1 a 2 +b 1 b 2 +c 1 c 2 = 0 .

По теме: методические разработки, презентации и конспекты

Практическая работа «Построение углов между плоскостями, между прямой и плоскостью»

Практическая работа по геометрии ,10 класс. Хотя данную работу можно провести при подготовке к ЕГЭ по математике, при решении задач типа С2. Работа содержит 8 заданий на построение угла между прямой и.

Тест по теме «Параллельность прямых и плоскостей. Перпендикулярность прямых в пространстве» (геометрия 10 класс)

Данный тест можно предложить учащимся как входной перед изучением темы «Многогранники».

Параллельность прямых и плоскостей. Параллельные прямые в пространстве

Урок-презентация по геометрии 10 класс.

Тесты по теме «Прямые в пространстве. Параллельность прямых, прямой и плоскости», «Перпендикулярность прямых, прямой и плоскости»

Тесты предназначены для проверки усвоенияследующих понятий и определений: взаимное расположение прямых в пространстве, определение скрещивающихся прямых, определение параллельных прямых, признак парал.

Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространстве

Материал для практической работы «Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространств.

Расстояние от точки до плоскости, от прямой до плоскости

Материал для практической работы «Расстояние от точки до плоскости, от прямой до плоскости&quot.

Составление уравнений сферы, плоскости, прямой.

Составление уравнений сферы, плоскости, прямой.

Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости. — презентация

Презентация была опубликована 8 лет назад пользователемЛиана Яхнова

Похожие презентации

Презентация на тему: » Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости.» — Транскрипт:

1 Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости.

2 Цели урока: Ввести понятие сферы, шара и их элементов Вывести уравнение сферы в заданной прямоугольной системе координат Рассмотреть возможные случаи взаимного расположения сферы и плоскости Формировать навык решения задач по теме

3 Окружность Окружность – множество точек плоскости, равноудаленных от данной точки Точка О – центр окружности ОА — радиус О А

4 Сфера Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки Точка О – центр сферы Данное расстояние – радиус сферы (обозначается R)

5 Сфера Отрезок, соединяющий две точки сферы и проходящий через ее центр – диаметр сферы (равен 2R) Сфера может быть получена вращением полуокружности (АСВ) вокруг ее диаметра (АВ) О

6 Шар Тело, ограниченное сферой, называется шаром Шаром радиуса R и с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек

7 Уравнение сферы Пусть R – радиус сферы С(х,у,z) – центр окружности Расстояние от произвольной точки М(х,у,z) до точки С найдем по формуле Если точка М лежит на данной сфере, МС = R, или Координаты точки М удовлетворяют уравнению

8 Решение задач 574(а) 576 (а) 577 (а) 578 (устно)

9 Взаимное расположение сферы и плоскости Обозначения R – радиус сферы d – расстояние от центра до плоскости α Плоскость Оху совпадает с плоскостью α, поэтому ее уравнение имеет вид z=0 Центр сферы С лежит на положительной полуоси Оz, т.е. имеет координаты С(0;0;d) Уравнение сферы

10 Взаимное расположение сферы и плоскости Если координаты произвольной точки М (х;у;z) удовлетворяют обоим уравнениям, то М лежит как в плоскости α, так и на сфере. Вопрос о взаимном расположении сводится к исследованию системы уравнений Подставив z = 0 во второе уравнение, получим

11 Взаимное расположение сферы и плоскости 1) d

12 Взаимное расположение сферы и плоскости 2) d = R

R» title=»Взаимное расположение сферы и плоскости 3) d > R» > 13 Взаимное расположение сферы и плоскости 3) d > R R»> R»> R» title=»Взаимное расположение сферы и плоскости 3) d > R»>

15 Домашнее задание п.64 – (в) 577 (в) 581

Презентация к уроку геометрии 11 класса по теме «Сфера и шар»

Определение сферы и шара, уравнение сферы, взаимное расположение сферы и плоскости, площадь сферы.

Просмотр содержимого документа
«Презентация к уроку геометрии 11 класса по теме «Сфера и шар»»

Учитель: Шамаева И. И.

Геометрия –11 класс

• Определение сферы, шара.
• Уравнение сферы.
• Взаимное расположение сферы и плоскости.
• Площадь сферы.
• Итог урока.

Окружность и круг

• Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии r от данной точки.

• Часть плоскости, ограниченная окружностью, называется кругом.

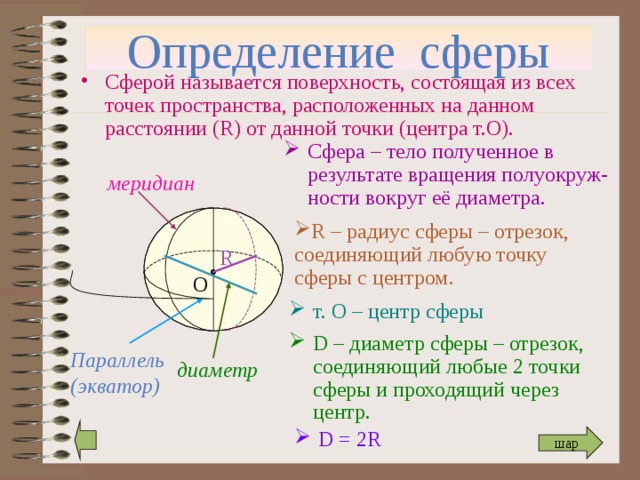
• Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ( R) от данной точки ( центра т.О).

• Сфера – тело полученное в результате вращения полуокруж-ности вокруг её диаметра.

• R – радиус сферы – отрезок, соединяющий любую точку сферы с центром.

• т. О – центр сферы

• D – диаметр сферы – отрезок, соединяющий любые 2 точки сферы и проходящий через центр.

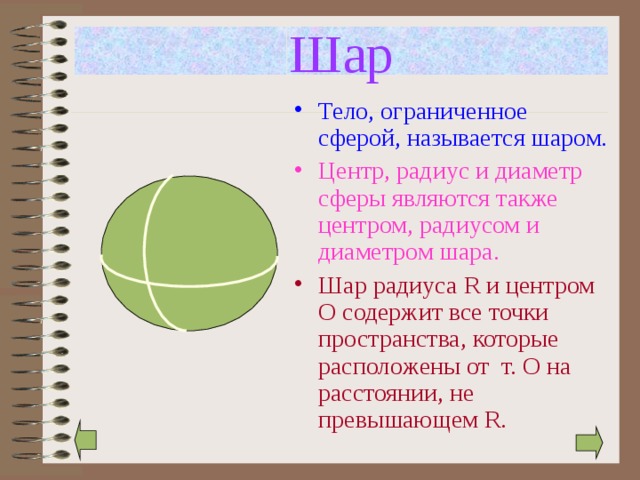
• Тело, ограниченное сферой, называется шаром.

• Центр, радиус и диаметр сферы являются также центром, радиусом и диаметром шара.

• Шар радиуса R и центром О содержит все точки пространства, которые расположены от т. О на расстоянии, не превышающем R.

Исторические сведения о сфере и шаре

• Оба слова « шар » и « сфера » происходят от греческого слова «сфайра» — мяч.
• В древности сфера и шар были в большом почёте. Астрономические наблюдения над небесным сводом вызывали образ сферы.
• Пифагорейцы в своих полумистических рассуждениях утверждали, что сферические небесные тела располагаются друг от друга на расстоянии пропорциональном интервалам музыкальной гаммы. В этом усматривались элементы мировой гармонии. Отсюда пошло выражение «музыка сферы».
• Аристотель считал, что шарообразная форма, как наиболее совершенная, свойственна Солнцу, Земле, Луне и всем мировым телам. Так же он полагал, что Земля окружена рядом концентрических сфер.
• Сфера, шар всегда широко применялись в различных областях науки и техники.

Как изобразить сферу?

• 1. Отметить центр сферы (т.О)

• 2. Начертить окружность с центром в т.О

• 3. Изобразить видимую вертикальную дугу ( меридиан)

• 4. Изобразить невидимую вертикальную дугу

• 5. Изобразить видимую гори-зонтальную дугу (параллель)

• 6. Изобразить невидимую горизонтальную дугу

• 7. Провести радиус сферы R

• Зададим прямоугольную систему координат Оxy

• Построим окружность c центром в т. С и радиусом r

• Расстояние от произвольной т. М ( х;у) до т.С вычисляется по формуле:

• МС = (x – x 0 ) 2 + (y – y 0 ) 2

МС = r , или МС 2 = r 2

окружности имеет вид:

(x – x 0 ) 2 + (y – y 0 ) 2 = r 2

• Зададим прямоугольную систему координат Оxyz

• Построим сферу c центром в т. С и радиусом R

МС = (x – x 0 ) 2 + (y – y 0 ) 2 + (z – z 0 ) 2

• МС = R , или МС 2 = R 2

сферы имеет вид:

(x – x 0 ) 2 + (y – y 0 ) 2 + (z – z 0 ) 2 = R 2

Задача 1. Зная координаты центра С(2;-3;0), и радиус сферы R=5 , записать уравнение сферы.

так, как уравнение сферы с радиусом R и центром в точке С(х 0 ;у 0 ; z 0 ) имеет вид (х-х 0 ) 2 + (у-у 0 ) 2 + ( z-z 0 ) 2 =R 2 , а координаты центра данной сферы С(2;-3;0) и радиус R=5 , то уравнение данной сферы ( x-2) 2 + (y+3) 2 + z 2 =25

Ответ: ( x-2) 2 + (y+3) 2 + z 2 =25

r d d = r Если d = r , то прямая и окружность имеют 1 общую точку. Если d Если d r , то прямая и окружность не имеют общих точек. Сфера и плоск » width=»640″

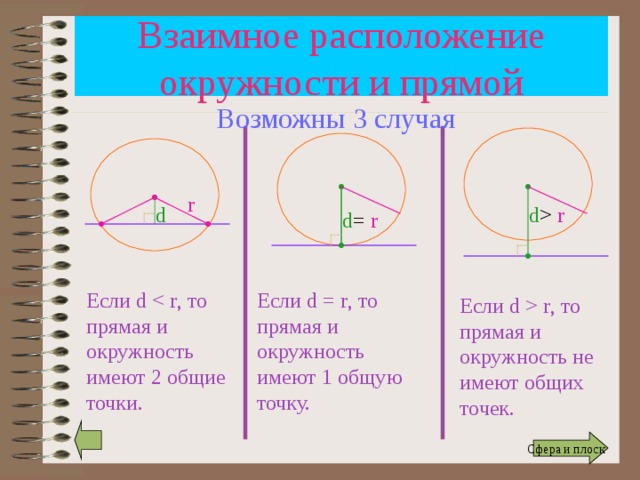
Взаимное расположение окружности и прямой

Возможны 3 случая

Если d = r , то прямая и окружность имеют 1 общую точку.

Если d r , то прямая и окружность не имеют общих точек.

Взаимное расположение сферы и плоскости

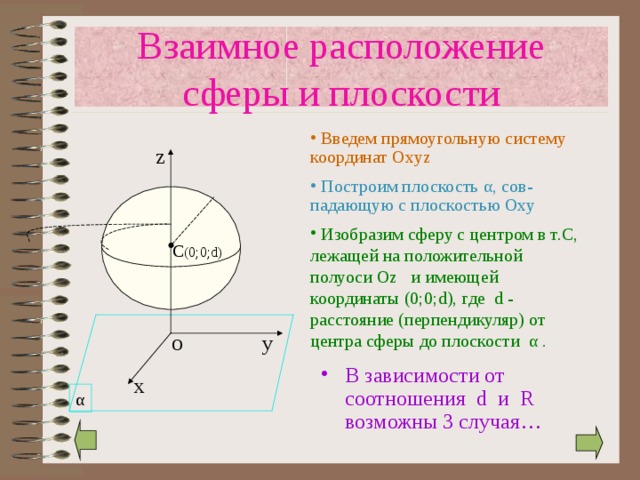
• Введем прямоугольную систему координат Oxyz

• Построим плоскость α , сов-падающую с плоскостью Оху

• Изобразим сферу с центром в т.С, лежащей на положительной полуоси Oz и имеющей координаты (0;0; d) , где d — расстояние (перпендикуляр) от центра сферы до плоскости α .

• В зависимости от соотношения d и R возможны 3 случая…

Взаимное расположение сферы и плоскости

• Сечение шара плоскостью есть круг.

• С приближением секущей плоскости к центру шара радиус круга увеличивается. Плоскость, проходящая через диаметр шара, называется диаметральной . Круг, полученный в результате сечения, называется большим кругом.

Взаимное расположение сферы и плоскости

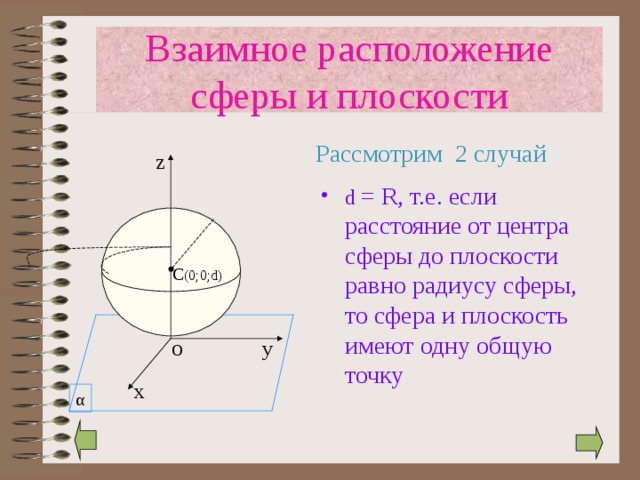
Рассмотрим 2 случай

• d = R , т.е. если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют одну общую точку

R , т.е. если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек. C (0 ;0; d) у O х α » width=»640″

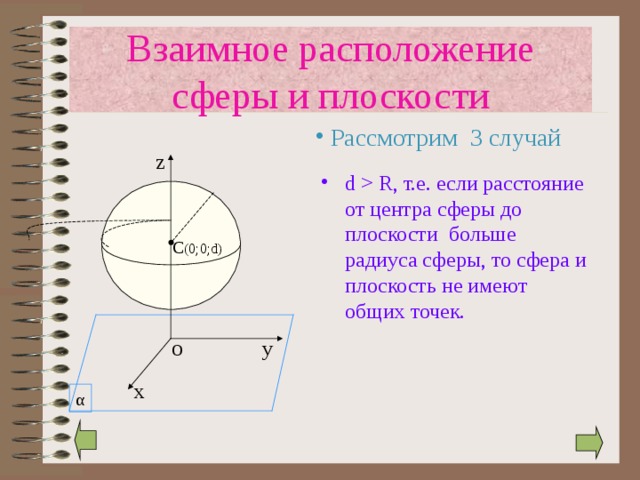
Взаимное расположение сферы и плоскости

• d R , т.е. если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Задача 2. Шар радиусом 41 дм пересечен плоскостью, находящейся на расстоянии 9 дм от центра. Найти радиус сечения.

Шар с центром в т.О

α — секущая плоскость

Рассмотрим ∆ ОМК – прямоугольный

ОМ = 41 дм; ОК = 9 дм; МК = r , r = R 2 — d 2

по теореме Пифагора: МК 2 = r 2 = 41 2 — 9 2 = 16 81 — 81=1600 отсюда r сеч = 4 0 дм

Ответ: r сеч = 4 0 дм

• Сферу нельзя развернуть на плоскость.

• Опишем около сферы многогран ник, так чтобы сфера касалась всех его граней.

• За площадь сферы принимается предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани

Площадь сферы радиуса R : S сф =4 π R 2

т.е.: Площадь поверхности шара равна учетверенной площади большего круга

S шара =4 S круга

Задача 3. Найти площадь поверхности сферы, радиус которой = 6 см.

• S сф = 4 π R 2
• S сф = 4 π 6 2 = 144 π см 2

Ответ: S сф = 144 π см 2

Первый советский искусственный спутник Земли был изготовлен в форме шара, диаметр которого равен 58 см.

Определить площадь поверхности спутника.

S = 4 π R 2 = 4 · 3,14 · 29 2 ≈ 10563 см 2 ≈

Ответ: Поверхность спутника равна 1м 2

Сколько метров шелковой материи шириной 1м надо для изготовления воздушного шара, радиус которого 2м? На соединение и отходы идет 10% материала.

S пов. = 4 π R 2 = 4 · 3,14 · 4 ≈ 50,24м 2

Т.к. ширина материи 1м, значит потребуется ≈ 50м материи.

1% составляет ≈ 0,5м

10% составляет ≈ 5м

Всего потребуется ≈ 55м материи

Сколько кожи пойдет на покрышку футбольного мяча радиуса 10 см? (На швы добавить 8% от площади поверхности мяча).

S сферы = 4 π R 2 , S = 4 π · 10 2 =40 π ( см 2 )

1% S составляет 0.01· 400 π = 4 π (см 2 );

8% S составляет 8 · 4 π = 32 π (см 2 );

S = 400 π + 32 π = 432 π ≈ 1357 (см 2 )

108% составляет 1,08 · 400 π = 432 π (см 2 )

Ответ: ≈ 1357 см 2 пойдет на покрышку футбольного мяча

Сегодня вы познакомились с:

• определением сферы, шара;

• уравнением сферы;
• взаимным расположением сферы и плоскости;
• площадью поверхности сферы.