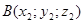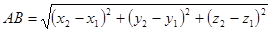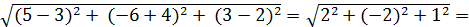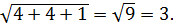Уравнение окружности сферы плоскости расстояние между точками

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ — Тема: Решение задач по теме: «Уравнение окружности, сферы, плоскости. Расстояние между точками»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Решение задач по теме: «Уравнение окружности, сферы, плоскости. Расстояние между точками»

— применить умения в использовании теоретических сведений для составления уравнений окружности, сферы, плоскости.

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

I Вариант II Вариант

1. Дан ∆ ABC с вершинами в точках Дан ∆ ABC с вершинами в точках

A (7; 3; -2) A (2; 0; 5)

B (1; 3; 6) B (3; 4; 0)

С (0; 0; -1). C (2; 4; 0).

Найти длину средней линии, Найти длину средней линии,

параллельной AB . параллельный BC .

2. Составить уравнение плоскости, Составить уравнение плоскости,

проходящей через точку А и проходящей через точку В и

перпендикулярный вектору AB , перпендикулярный вектору AB ,

если А(2; 3; -4), В(-1; 2; 2). если А(-2; 1; 3), В(1; -2; 4).

3. Сфера задана уравнением

( x -1) 2 + y 2 +( z -2) 2 = 9 x 2 +( y +3) 2 +( z -2) 2 = 25

a ) Назовите координаты центра и радиус сферы.

б) Определите, принадлежит ли данной сфере точки:

1. Внимательно прочитать тему и цель практической работы .

2. Изучить учебный материал по теме.

3. Ответить на вопросы.

4. Выполнить задания.

5. Подготовить отчет.

Пояснения к работе (учебный материал):

1.Расстояние между точками.

,

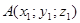
AB =

2. Уравнение плоскости.

Уравнение плоскости, проходящей через данную точку и перпендикулярной данному вектору.

Ненулевой вектор n, перпендикулярный плоскости, называют ее нормальным вектором. Если дана точка М(х₀;у₀; z ₀) и нормальный вектор n = (A, B, C) плоскости, то ее уравнение имеет вид A ( x — x ₀ ) + B ( y — y ₀) + C ( z — z ₀)

Равенство выражает необходимое и достаточное условие перпендикулярности двух векторов n и M ₀ M .

— уравнение окружности с центром в начале координат и радиусом r.

— уравнение окружности с центром в точке и радиусом r.

— уравнение сферы в точке с центром и радиусом R.

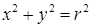
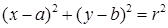
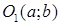
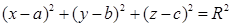
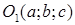
При выполнении практической работы рассмотрите следующие примеры:

Дан ∆АВС с вершинами в точках А(3; -4; 2), В(-5; 6; 7), С(5; -6; 3).

Найти длину средней линии, параллельной АС.

MN — средняя линия

AC =

=

Составить уравнение плоскости, проходящей через точку M (1; -2; 4) и перпендикулярный вектору MN , N (3; 4; 5).

MN=(3-1; 4+2; 5-4); MN=(2; 6; 1); a=2; b=6; c=1.

Сфера задана уравнением

( x +2) 2 +( y -5) 2 + z 2 =16.

а) Назовите координаты центра и радиус сферы.

б) Определите принадлежат ли данной сфере точки: А(-2; 9; 0) и В(1; 3; 2)

а) (-2; 5; 0) – координаты центра.

R = 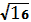= 4.

(-2+2) 2 +(9-5) 2 +0 2 =16

А принадлежит сфере.

(1+2) 2 +(3-5) 2 +2 2 =16

В не принадлежит 17=16 (неверно).

Вопросы для закрепления теоретического материала к практическому занятию:

1. Записать формулу расстояния между точками.

2. Уравнение плоскости.

3. Уравнение окружности.

4. Уравнение сферы.

Название практической работы.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

1. Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2. Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7. Башмаков М.И. Математика: Учебник. — М., 2016.

5.6.2 Формула расстояния между двумя точками; уравнение сферы

Видеоурок: Формула расстояния между двумя точками

Лекция: Формула расстояния между двумя точками; уравнение сферы

Расстояние между двумя точками

Для нахождения расстояния между двумя точками на прямой в предыдущем вопросе мы использовали формулу d = х₂ – х_1.

Но, что касается плоскости, дела обстоят иначе. Не достаточно просто найти разность координат. Для нахождения расстояния между точками по их координатам следует воспользоваться следующей формулой:

Например, если у Вас имеются две точки с некоторыми координатами, то найти расстояние между ними можно следующим образом:

АВ = ((4 + 4) 2 + (-1 – 6) 2 ) 1/2 ≈ 10,6.

То есть для вычисления расстояния между двумя точками на плоскости необходимо найти корень из суммы квадратов разностей координат.

Если необходимо найти расстояние между двумя точками на плоскости, следует воспользоваться аналогичной формулой с дополнительной координатой:

Уравнение сферы

Для задания сферы в пространстве следует знать координаты её центра, а также её радиус, чтобы воспользоваться следующей формулой:

Данное уравнение соответствует сфере, центр которой находится в начале координат.

Если же центр сферы сдвинут на некоторое количество единиц по осям, то следует воспользоваться следующей формулой: