Уравнение окружности в векторной форме

Уравнение дуги окружности в векторной форме записи

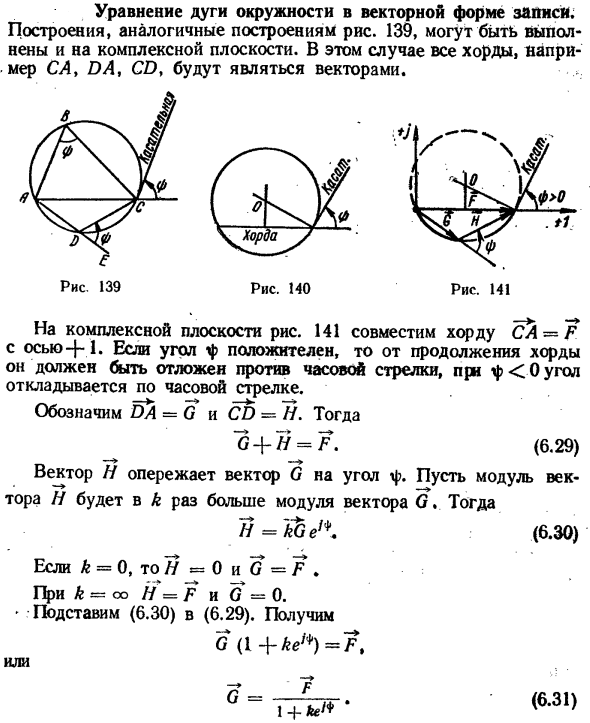
Уравнение дуги в векторной нотации. Структура 139, аналогичная структуре рисунка, может быть выполнена на комплексе plane. In в этом случае весь код, такой как SL, PL, SP и т. д. будут векторы.

Указывает DA = G и CD = N. — Г + Ч = Ф(6.29） Вектор H более продвинут на угол f, чем вектор G. модуль вектора H умножается на K модуля вектора G. H = кг A(6.30） Если Λ= 0, то 7? = 0 и G =? 。 если k-co H = F и G-0. Заменить ’(6.29) на ’ (6.30).Возьми Г(1 -] — ке^) = Ф Или X 7 (6.31）

Уравнение (6.31) называется уравнением дуги окружности в векторной системе счисления. * ?.-•••

Если коэффициент£изменяется от 0 до Людмила Фирмаль

Важно отметить, что рабочая часть окружности или рабочая дуга-это та часть окружности, которая находится по другую сторону касательной к хорде F(рабочая дуга на рисунке 141 нарисована сплошной линией, а не сплошной линией).

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Окружность в векторной форме

Уравнение дуги окружности в векторной форме записи

На комплексной плоскости рисунка 141 хорда C A-F совместима с осью 4 * h, если φ Людмила Фирмаль

Уравнение (6.31) называется уравнением дуги окружности в векторной системе счисления. * ?.-•••

Если коэффициент£изменяется от 0 до Людмила Фирмаль

Образовательный сайт для студентов и школьников

Уравнение дуги окружности в векторной форме записи

Построения, аналогичные построениям на рис. 4.18, а, могут быть выполнены и на комплексной плоскости. В этом случае все хорды, например СА, DA, DC, являются векторами.

На комплексной плоскости (рис. 4.18, в) совместим хорду CA = F с осью +1. Если угол |/ > 0, то от продолжения хорды его откладывают против часовой стрелки; если р 90°.

Круговые диаграммы

Из параграфа 3.4 известно, что синусоидально изменяющиеся функции времени (токи, напряжения) могут быть изображены векторами на комплексной плоскости. Если процесс в электрической цепи описывается уравнением, по форме тождественным уравнению (4.69), то геометрическим местом концов вектора тока (напряжения), выполняющего в уравнении электрической цепи те же функции, что и вектор G в уравнении (4.69), является окружность.

Под круговой диаграммой тока или напряжения понимают дугу окружности, являющуюся геометрическим местом концов вектора тока (напряжения) при изменении по модулю какого-либо сопротивления электрической цепи и сохранении неизменными остальных сопротивлений, частоты и ЭДС источников энергии.

С помощью круговых диаграмм производят графический анализ работы электрических цепей.

Циркулярные кривые 2-го порядка

Как известно, кривыми Безье нельзя построить дугу окружности или эллипса. В этой статье рассматриваются кривые, лишённые такого недостатка.

Кривые Безье

Логика построения кривых Безье хорошо понятна из следующей анимации:

Чтобы получить формулу непосредственно из графического представления, достаточно определить вспомогательную функцию для линейной интерполяции между двумя точками, в которая при изменении параметра t от 0 до 1 возвращает промежуточные значения от a до b:

С её помощью можно последовательно найти необходимые точки — сначала найти

а затем уже через них найти

При желании, можно подставить функции друг в друга и сократить — хотя это особо и не упростит вычисления, зато позволит обобщить кривые на произвольное количество опорных точек (через полиномы Бернштейна). В нашем случае получим

Увеличение порядка кривых достигается тривиально — исходные точки задаются не константно, а как результат интерполяции между n+1 других контрольных точек:

Циркулярные кривые

Дуга окружности

Чтобы похожим образом построить дугу окружности, необходимо определить соответствующую логику построения — по аналогии с черчением окружности циркулем.

Изначально нам неизвестен центр окружности d — он находится через пересечение перпендикуляров к касательным в точках a и b (далее узловых); сами же касательные задаются с помощью точки c (далее направляющей). Для построения произвольной дуги окружности (меньшей 180°) достаточно, чтобы расстояния от направляющей точки до узловых были одинаковыми.

Дуга эллипса

Построить дугу эллипса уже посложнее — потребуется два вектора, вращающихся в разные стороны (подробнее здесь)

Используя озвученный выше способ нахождения точки d, мы уже не можем построить произвольную дугу эллипса — только лишь от 0° до 90° (в том числе и повёрнутую на некоторый угол).

Дуга гипотрохоиды

Задав условие, что в начале и конце черчения векторы должны лежать на одной прямой, мы получим дугу гипотрохоиды во всех остальных случаях. Это условие не случайно и (помимо однозначного определения кривой) гарантирует совпадение касательных в узловых точках. Как следствие, угловые пути, которые проходят оба вектора, станут разными, но в сумме по-прежнему будут давать 180°.

Как изменяется форма кривой в зависимости от положения направляющей точки, можно посмотреть на следующей анимации:

Алгоритм

Поскольку здесь мы имеем вращения на двумерной плоскости, математику построения этих кривых удобно описывать через комплексные числа.

1) находим точку пересечения нормалей касательных, проведённых от направляющей точки к узловым:

(здесь звёздочка означает комплексное сопряжение).

2) зная d, находим длины нормалей

и их сумму и разность

3) находим единичный вектор, от которого начинается построение

4) находим угловые пути, которые должны пройти каждый из векторов

При умножении векторов их длины умножаются, а углы — складываются. Здесь деление используется для противоположной задачи — найти разницу углов, т. е. угол между векторами.

Поскольку для функции аргумента длина вектора не играет роли, тот же результат можно получить и заменив деление умножением на комплексно сопряжённый вектор — такой вариант даже предпочтительнее, поскольку будет более численно устойчив на очень малых значениях из-за отсутствия деления; здесь же выбор в пользу деления сделан исключительно ради наглядности.

Здесь имеется ещё один крайне важный момент. Если бы мы сначала нашли углы для каждого вектора по отдельности, а потом бы считали разницу как

— результат не всегда был бы корректным из-за многозначности функции аргумента.

5) последовательно изменяя t от 0 до 1 с некоторым шагом, находим принадлежащую кривой точку по формуле

Циркулярные сплайны

Так же, как и кривые Безье, эти кривые можно совмещать для кусочно-непрерывного построения сплайнов. Для обеспечения гладкости в узловых точках (стыковки) необходимо, чтобы узловая точка находилась на одной линии с двумя соседними направляющими точками. Для этого можно задавать узловые точки не явным образом, а через интерполяцию направляющих точек. Их также можно не задавать вообще, вычисляя полностью автоматически — например, как среднее между направляющих точек:

Справа для сравнения использован тот же подход с кривыми Безье 2-го порядка.

Замечания и нюансы

В отличие от кривых Безье, здесь кривая не всегда лежит внутри фигуры из линий, соединяющих контрольные точки, например

Кроме того, существует вырожденный случай, который необходимо обрабатывать отдельно — когда направляющая точка лежит на одной прямой с узловыми точками. При этом кривая вырождается в прямую, а при попытке вычислить точку d возникает деление на ноль.

У этих кривых также имеется ограничения на кривизну линии, поскольку в соответствии с алгоритмом выбирается наименьший путь следования и кривая не может обогнуть больше, чем 180°. Это приводит к тому, что при кусочно-непрерывной интерполяции могут возникать острые углы при определённом положении направляющих точек (справа — те же точки для Безье):

Заключение

Дальнейшим развитием рассмотренного метода построения кривых является увеличение количества векторов, участвующих в построении кривой и, соответственно, увеличение количества направляющих точек. Однако, в отличие от кривых Безье, повышение порядка здесь не является очевидным и требует отдельного вдумчивого размышления. Также возможны различные методы комбинации их с кривыми Безье — в частности, интерполяции центра окружности рисующих векторов.

Рассмотренный метод построения кривых также не является единственным, частным случаем которого являются дуги окружности и эллипса — как минимум, эллипс можно построить через пересечение прямых в параллелограмме (правда, в этом варианте автор потерпел неудачу). Возможно, что существуют и другие решения, в том числе и варианты описанного в статье — пишите в комментариях, если вам что-то известно на эту тему.

Исходный код статьи можно скачать на GitHub.

Уравнение окружности в векторной форме

ОКРУЖНОСТЬ – ЭТО КОМПЛЕКСНАЯ КРИВАЯ ВТОРОГО ПОРЯДКА

Окружность относят к элементарным кривым, настолько простым, что её исследованием никто не занимался. В статье сделана попытка исследования уравнения окружности и её графика в декартовой системе координат. В результате выяснено, что окружность – это комплексная кривая, которая формируется частично действительными переменными, а частично мнимыми. Соответственно, на окружности существуют точки перехода между действительными и мнимыми областями пространства. Выявленные точки перехода являются точками разрыва функций переменных в уравнении окружности. Последнее значит, что интегрирование и дифференцирование по окружности – это недопустимые математические действия со всеми вытекающими отсюда последствиями.

В математике линия окружности определяется, чаще всего, как геометрическое место точек плоскости , удалённых от некоторой точки – центра окружности – на заданное расстояние , называемое радиусом окружности . Уравнение окружности в декартовых прямоугольных координатах с центром в начале координат обычно записывают в виде [1]:

(1)

где константа R – радиус окружности. В полярных координатах уравнение окружности описывается через полярный угол t и полярный радиус ρ и имеет вид:

при 0≤ t ≤2 π (2)

На рис.1 показана окружность, центр которой совмещён с центром декартовой системы координат и полярной. На рисунке полярная ось 0 ρ совпадает с осью 0 x , а полярный угол t изменяется от 0 до 2 π . При этом радиус окружности обходит контур против часовой стрелки, как это положено в полярной системе координат [1], т.е. по кривой abcda.

При таком расположении осей переход от полярных координат к декартовым принято записывать соотношениями [1]:

(3)

Считается, что система уравнений (3) представляет собой параметрическое уравнение окружности [1]. Однако, из этой системы уравнений вытекает, что при t=nπ, где n – число натурального ряда и 0, она вырождается в уравнение:

(4)

А при t=nπ+π/2 система уравнений (3) вырождается в уравнение:

(5)

Если рассмотреть уравнение (1), то оно точно так же при t=nπ/2 вырождается в уравнения:

(6) и (7)

А это значит, что в точках окружности, где t=nπ/2 перестают действовать уравнения (1) и (3), которые переходят в (4)-(5) и (6)-(7). Ещё более радикальный результат получается при решении системы уравнений способом, который обычно не используется при определении радиуса. Для этого достаточно перемножить правые и левые части исходных уравнений (3). В этом случае, с учётом того, что , получаем выражение:

( 8 )

( 9 )

Как видно из формулы (9) величина радиуса имеет нелинейную зависимость как от переменной x , так и от переменной y . Именно об этом шла речь в статье [2]. Также из уравнения (9) вытекает обязательное условие sin 2 t ≠0 или t ≠ nπ /2 – недопустимость деления на 0. А это значит, что величина радиуса в декартовых координатах, выраженная через зависимости системы уравнений (3), не определена при значениях полярного угла t = nπ /2 . Поэтому радиус окружности из формулы (9) при значениях полярного угла t = nπ /2 необходимо доопределять, что и сделано в (4) и (5). Учитывая сказанное выше, получаем более полную и более точную систему уравнений перехода от полярных координат к декартовым, или систему параметрических уравнений окружности:

(10)

Исходя из более полной системы параметрических уравнений окружности (10), получаем, что окружность на плоскости декартовой системы координат не является непрерывной функцией. У неё существуют четыре точки разрыва для функций переменных x и y , которые соответствуют значениям параметра t=nπ/2. В этих точках происходит замена уравнения окружности (1) и параметрических уравнений (3) уравнениями (6) и (7) или (4) и (5). Т.е. график окружности не может быть представлен непрерывной функцией в декартовой системе координат, потому что описывается несколькими разными функциями – система уравнений (10) как минимум.

Итак, окружность не является элементарной кривой на плоскости в декартовой системе координат. Но и система уравнений не является полным и точным описанием окружности. Потому что полученная выше система уравнений (10) определяет только скалярый аспект или абсолютные значения определённых функций и переменных, характеризующих окружность. А есть ещё упоминание о направлении – например, направление обхода контура. Когда у линии существует направление – она считается векторной величиной. А векторное представление окружности и, соответственно, радиуса – это реальность.

Во-первых, представление направленного замкнутого контура наглядно просматривается в полярной системе координат. Основная характеристика полярной системы координат – это полярный угол t. Величина полярного угла изменяется в пределах от 0 до 360° или 2π. Соответственно, существует направление изменения полярного угла, принятое как положительное (в полярных координатах – против часовой стрелки) [1]. Естественно, что направление обхода контура круга или окружности совпадает с направлением возрастания полярного угла в полярной системе координат. Очевидно, что направление обхода контура должно быть отражено и в функциях, представляющих окружность в декартовой системе координат. Это является важным этапом в исследовании окружности.

Но если есть направление у окружности, то существует направление и у радиуса, поскольку радиус однозначно связан с контуром или окружностью соответствующими формулами. Если исходить из представления окружности в полярной системе координат, все радиусы должны исходить из центра окружности. Исключение составляет радиус-вектор в небесной механике. Начало радиус-вектора орбиты небесного объекта привязано к центру притяжения, а окончание – к небесному телу на линии орбиты [3]. Таким образом, радиус окружности (орбиты) также как и линия окружности является вектором.

С точки зрения векторной алгебры, уравнение (1) – это формула определения скалярной величины радиуса окружности. В этом случае векторная форма записи определения радиуса окружности в соответствии с уравнением (1) имеет вид:

(11)

Вполне естественно, что векторы и имеют направления, которые совпадают с направлением соответствующей оси в декартовой системе координат. При этом следует помнить, что переменные x и y имеют параметрическую зависимость от полярного угла t в соответствии с (10). И, если следовать формуле (11) и правилам векторного сложения [1], то для полярных углов t=30°, 120°, 210° и 300° получаем такие векторы суммы переменных, как показано на диаграммах рис.2. Точки M, K, L, N на окружности рис.2 отмечают перечисленные выше углы.

Как видно из диаграмм рис.2 только один вектор суммы из полученных четырёх векторов расположен, как в полярной системе координат. “Правильный” радиус получен сложением векторов и , которые берут начало из центра окружности или центра системы координат. Т.о. чтобы радиусы в остальных секторах окружности исходили из центра окружности, необходимо, чтобы слагаемые их векторы переменных исходили из центра декартовой системы координат. Однако, в декартовой системе координат это условие выполнимо только для положительных полуосей переменных – что хорошо видно на рис.2.

С другой стороны, необходимое направление координатных полуосей можно получить, используя переменные мнимой области пространства. Т.е. вместо отрицательных полуосей декартовых координат следует ввести оси, полученные через мнимые значения переменных и мнимый полярный угол. Объяснить такой переход просто – он следует из определения мнимой единицы [1]:

(12)

Из него вытекает, что дважды мнимое число – это отрицательное действительное число. Таким образом, дважды мнимые переменные обязательно находятся в области действительных чисел. Для векторных величин дважды мнимость формирует поворот вектора на 180º.

В нашем случае мнимые переменные из (3) можно записать через мнимую величину радиуса и мнимый угол и преобразовать следующим образом:

(13) и

(14)

Поэтому дважды мнимые переменные имеют отрицательные величины и располагаются на действительных осях, направленных в сторону от центра координат. Это даёт нам систему совмещённых координат, которая состоит из четырёх полуосей – двух действительных и двух дважды мнимых. При этом все четыре полуоси исходят из центра координат, что отличает её от декартовой системы координат. И как результат – все радиусы и радиус-векторы имеют правильное расположение – связывают центр с линией окружности. Это хорошо видно на рис.3, где мнимые переменные показаны штриховыми линиями.

Учитывая всё вышеизложенное, получаем, что окружность, расположенная в области действительных чисел наполовину строится мнимыми (дважды мнимыми) переменными. Поэтому система координат при формировании окружности является совмещённой – состоит из двух действительных полуосей и двух дважды мнимых. Естественно, полное описание параметрических уравнений окружности должно иметь вид, отличный от (10), поскольку половина переменных происходит из мнимого пространства. Но это уже вопрос к специалистам.

Что характерно, в области мнимых чисел точно так же формируется окружность. При этом мнимая окружность наполовину строится при содействии действительных величин, которые остались незадействованными на действительной плоскости. Для области мнимых чисел система координат также будет совмещённой – две собственных мнимых полуоси и две из действительной области. Таким образом, две окружности – и мнимая и действительная – формируются одновременно усилиями мнимых и действительных переменных, т.е. дополняют одна другую. Поэтому окружность нельзя назвать однозначно действительной или однозначно мнимой кривой – она всегда комплексная и в области действительных и в области мнимых значений параметров.

И ещё одно замечание. На рис.3 хорошо видно, что центр окружности, для которого x =0 и y =0 , а также точки окружности, для которых x =0 или y =0 , являются точками перехода между мнимыми и действительными областями пространства. Последнее ещё раз подтверждает, что уравнение окружности имеет точки разрыва. В первую очередь это значит, что математические действия интегрирования и дифференцирования по окружности – и rot( a ) – являются недопустимыми математическими действиями, такими как деление на 0. А также это значит, что основные формулы теории электромагнитного поля следует переосмыслить заново.

Понятно, что из-за недостаточно глубокого исследования обычной окружности, математика и физика упустила многое в своих теориях. Поэтому более глубокое исследование функции окружности и её графика с внесением соответствующих корректив в существующие формулы просто необходима. Если восполнить этот пробел, то математики увидят, что решением задачи Пуанкаре о 3-сфере являются две сферы, соединённые через точку пережима (перехода), как это доказал в 80-ых годах прошлого столетия математик Колумбийского университета Ричард С.Гамильтон. А физики поймут, что существование электромагнитного поля невозможно без дополнения его виктори-полем [4]. И ещё многое другое прояснится в теориях и даст свои плоды на практике.

Мысли вслух : интересно, а другие кривые второго (и третьего) порядка тоже являются комплексными кривыми? – и что из этого вытекает?

источники:

http://b4.cooksy.ru/articles/okruzhnost-v-vektornoy-forme

http://www.sciteclibrary.ru/texsts/rus/stat/st5633.htm