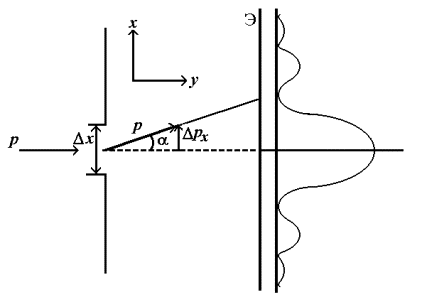
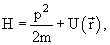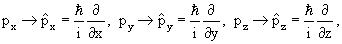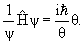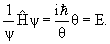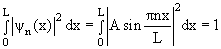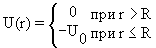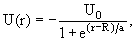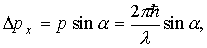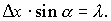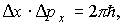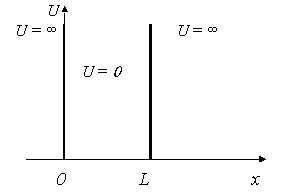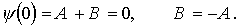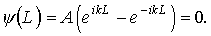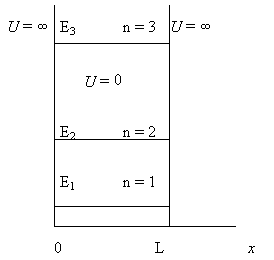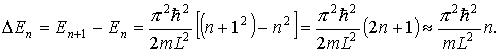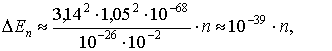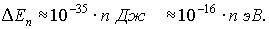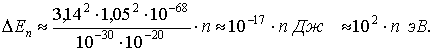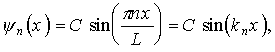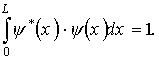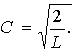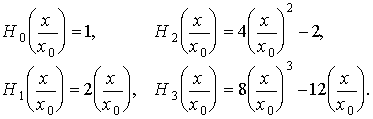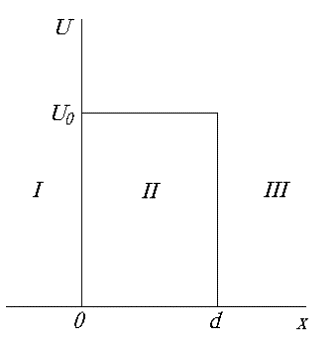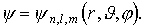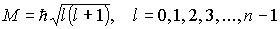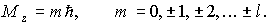Уравнение описывающее состояние свободной микрочастицы
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
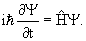 | (4.1) |
где 
в которой 







х → 


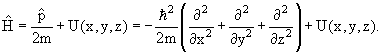 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


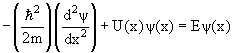
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
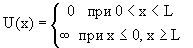 | (4.5) |
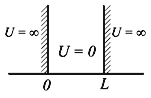
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
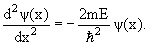 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
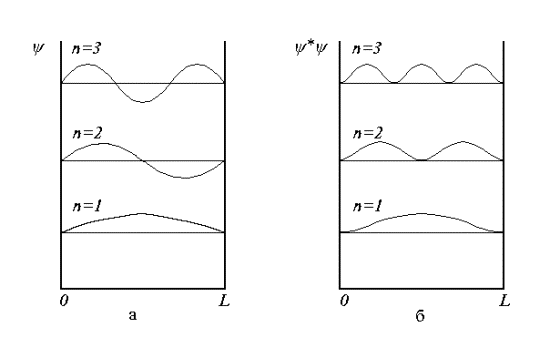
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
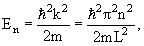 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
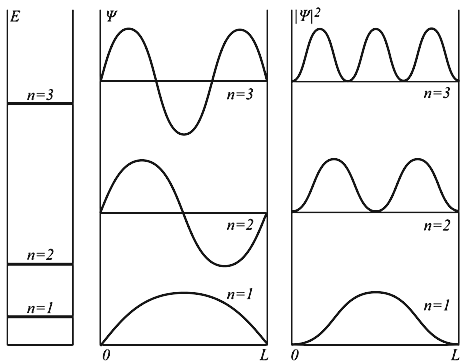
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
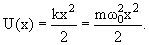 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
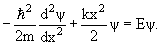 | (4.12) |
Допустимые значения полной энергии определяются формулой
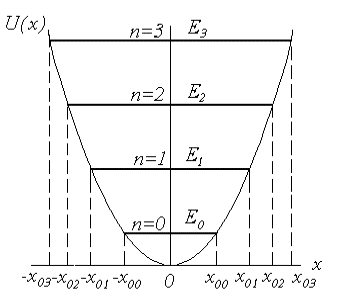
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
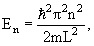

Одномерный гармонический осциллятор:
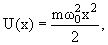
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
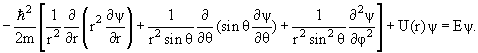 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
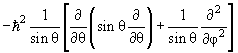 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 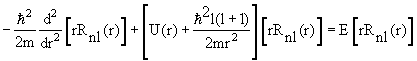 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
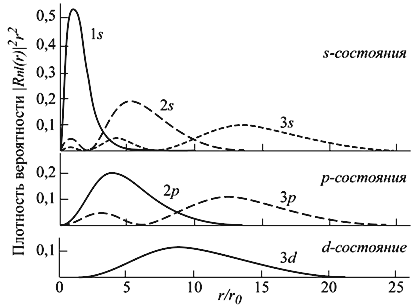
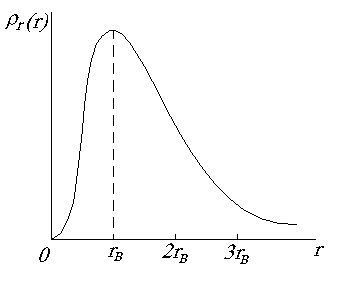
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
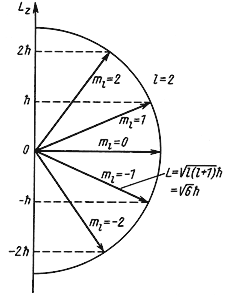
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
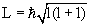 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
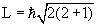
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Уравнение Шредингера. Уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях
Уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого вытекали бы волновые свойства частиц. Оно должно быть уравнением относительно волновой функции Ψ(х, у, z, t), так как величина │Ψ│ 2 определяет вероятность пребывания частицы в момент времени в объеме.
Основное уравнение сформулированоЭ. Шредингером: уравнения не выводится, а постулируется.
Уравнение Шредингера имеет вид:
— 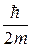
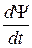
где ħ=h/(2π), т—масса частицы, Δ—оператор Лапласа, i— мнимая единица,U(x,y,z,t) — потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x,y, z, t) — искомая волновая функция частицы.
Уравнение (32.9) является общим уравнением Шредингера. Его также называют уравнением Шредингера, зависящим от времени. Для многих физических явлений, происходящих в микромире, уравнение (33.9) можно упростить, исключив зависимость Ψ от времени, иными словами, найти уравнение Шредингера для стационарных состояний — состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т. е. функцияU(x,y,z,t) не зависит явно от времени и имеет смысл потенциальной энергии.
∆Ψ + 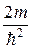
Уравнение (33.10) называется уравнением Шредингера для стационарных состояний.
В это уравнение в качестве параметра входит полная энергия Е частицы. Решение уравнения имеет место не при любых значениях параметра Е, а лишь при определенном наборе, характерном для данной задачи. Эти значения энергии называются собственными. Собственные значения Е могут образовывать как непрерывный и дискретный ряд.
33.5. Частица в одномерной прямоугольной «потенциальной яме с бесконечно высокими «стенками»
Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенциальная энергия частицы U (х) = соnstи ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. Энергия свободной частицы может принимать любые значения, т. е. ее энергетический спектр является непрерывным. Свободная квантовая частица описывается плоской монохроматической волной де Бройля, и все положения свободной частицы в пространстве являются равновероятными.

где l — ширина «ямы», а энергия отсчитывается от ее дна (рис.33.1).
Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде
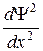
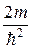
По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х=0 и х=l) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид
В пределах «ямы» уравнение Шредингера сведется к уравнению
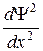
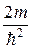
Стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Еп зависящих от целого числа п.
Еп= 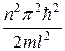
Следовательно, энергия Еп частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Еп — называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Еп, или, как говорят, частица находится в квантовом состоянии п. Частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная 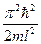
Туннельный эффект
Рассмотрим простейший потенциальный барьер прямоугольной формы (рис.33.2.а) для одномерного (по оси х) движения частицы. Для потенциального барьера прямоугольной формы высоты U ширины l можем записать
0, х 1(для области 3),

Таким образом, квантовая механика приводит к специфическому квантовому явлению, получившему название туннельного эффекта, в результате которого микрообъект может «пройти» сквозь потенциальный барьер.
Для описання туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих.
Решение уравнения Шредингера для прямоугольной потенциального барьера дает формулу для коэффициента прозрачности:
D = D0 exp( — 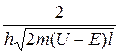
где U — высота потенциального барьера, Е — энергия частицы, l — ширина барьера, D0— постоянный множитель, который можно приравнять единице. Из этого выражения следует, что D сильно зависит от массы частицы, ширины барьера и от (U — Е); чем шире барьер, тем меньше вероятность прохождения сквозь него частицы.
С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия может сказаться достаточной для того, чтобы полная энергия частицы сказалась больше потенциальной.
Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например, a-распад, протекание термоядерных реакций).
ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
1.1. Экспериментальные и теоретические предпосылки квантовой
Теоретическим фундаментом физической электроники являются современные представления о поведении электронов, атомов и молекул, взаимодействующих между собой и с внешними силовыми полями. Многие свойства свободных частиц и многие физические процессы с участием этих частиц могут быть поняты только на основе квантово-механического описания состояния этих объектов.
Три основные проблемы, стоящие в центре внимания физиков в конце XIX — начале ХХ вв. – это проблема излучения абсолютно черного тела, проблема фотоэлектрического эффекта и проблема строения и стабильности атомов — привели в конечном итоге к созданию современных представлений о природе микрочастиц — объектов, подчиняющихся законам квантовой механики.
Проблема теплового излучения абсолютно черного тела возникла в связи с невозможностью объяснить с позиций классической физики зависимость интенсивности излучения абсолютно черного тела от длины электромагнитной волны. В частности, из законов классической физики следовал вывод о том, что интенсивность излучения должна монотонно расти с частотой и, следовательно, полное излучение должно быть бесконечно большим. Это означает также, что при любой температуре тепловое равновесие между излучением и веществом невозможно, что противоречит опыту.
В 1900 году М. Планку удалось вывести закон излучения абсолютно черного тела, снимающий эту проблему. Для этого ему необходимо было предположить, что осциллятор с собственной частотой w может получать или отдавать энергию только порциями (квантами), минимальная величина которых равна
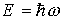
здесь ћ — новая фундаментальная константа, ћ = 1,054·10 -34 Дж·с.
Постоянная Планка является универсальной количественной характеристикой минимального воздействия между объектами природы, т. е. элементарным квантом действия. Гипотеза Планка явилась по существу распространением принципа атомизма на воздействие материальных объектов друг на друга. Так же как существует неделимая минимальная порция элемента, сохраняющая все его химические свойства, — атом и элементарный заряд, играющий роль «кванта», т. е. неделимой, минимальной порции заряда, так же существует минимальная «порция», «атом» или квант действия, равныйћ w и для воздействия материальных объектов друг на друга . В этом физический смысл гипотезы Планка. Ввиду малости величины ћ квантовый характер воздействия не проявляется для макроскопических тел, так же как не проявляются дискретность массы и заряда в опытах с макроскопическими телами.
На основании своей гипотезы М. Планк получил формулу для плотности энергии электромагнитного излучения абсолютно черного тела:
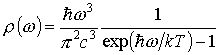
где с — скорость света; к — постоянная Больцмана; Т — абсолютная температура.
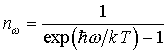
определяет среднее число квантов теплового излучения, приходящихся на данный тип колебаний.
Проблема фотоэффекта связана с существованием его красной границы по частоте и тем экспериментальным фактом, что кинетическая энергия фотоэлектронов не зависит от интенсивности света, а зависит только от его частоты. С классической точки зрения увеличение интенсивности света приводит к возрастанию амплитуды электромагнитной волны и, следовательно, электроны в металле в результате взаимодействия с этой волной должны ускоряться до больших скоростей, тем самым увеличивая свою кинетическую энергию.
Явление фотоэффекта было объяснено в 1905 г. А. Эйнштейном, который, развивая идею М. Планка, предположил, что энергия в пучке монохроматического света состоит из квантов, величина которых равна ћ w , где w — частота света. Тем самым дискретность энергии осциллятора связана с более фундаментальным фактом — само электромагнитное излучение состоит из отдельных квантов, несущих энергию ћ w . Это предположение приводит к известной формуле Эйнштейна для фотоэффекта:
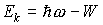
где Ек — кинетическая энергия фотоэлектрона; W — работа выхода электрона из данного вещества; ћ w — энергия кванта электромагнитного поля — фотона.
С точки зрения классических законов физики непонятна устойчивость атома и линейчатый характер атомных спектров. Электрон в планетарной модели атома, установленной в 1910 г. Э. Резерфордом, как имеющий заряди движущийся с ускорением, должен по законам классической электродинамики излучать энергию в виде электромагнитных волн, терять скорость и в конце концов упасть на ядро. Время падения электрона порядка 10 -9 с. Совокупность таких атомов должна давать сплошной спектр излучения, а не линейчатый, наблюдаемый на опыте.
Успех в устранении этих противоречий был достигнут Н. Бором в 1913 г., когда он распространил идеи Планка и Эйнштейна о квантовых свойствах электромагнитного излучения на атомы вещества. Н. Бор первым понял, что дискретные значения энергии не столько связаны с электромагнитным излучением или поглощением энергии атома, а являются его внутренним фундаментальным свойством. Свои выводы он сформулировал в виде известных постулатов — постулата о стационарных орбитах электронов в атоме, на которых электрон может находиться бесконечно долго не теряя энергию, и постулата, определяющего частоту излучения или поглощения электромагнитной энергии при переходе электрона в атоме с одной стационарной орбиты на другую.
Следует отметить, что в атоме Бора и квантование энергии атома, и требование стационарности орбит было связано с постоянной Планка. Стало понятным, что постоянная Планка и связанного с ней понятие элементарного кванта действия играют фундаментальную роль при описании поведения микрообъектов.
1.2. Гипотеза де Бройля. Корпускулярно-волновой дуализм микрочастиц
Теория Бора явилась важным шагом в понимании природы микромира. Она явилась основой оптической спектроскопии, объяснила строение атома водорода, обосновала периодичность химических свойств элементов и др. Однако эта теория с самого начала рассматривалась как промежуточный этап для построения более общей теории, в которой были бы обоснованы правила квантования, постулированные Н. Бором.
Принципиальный шаг к новой теории сделал в 1925 г. Луи де Бройль. Он распространил представление о двойственной природе света на все микрочастицы материи — электроны, протоны, атомы и т. д. Еще в классической физике ряд оптических явлений интерпретировался с точки зрения на свет как на волновой процесс (интерференция, дифракция). С другой стороны, некоторые явления с участием света могли быть поняты только на основе представлений о свете как потоке частиц (корпускул) (фотоэффект, эффект Комптона и др.). Нетрудно установить соотношение между массой фотона m — частицы света и частотой электромагнитной волны света w , характеризующей его волновые свойства. В соответствии с известным соотношением Эйнштейна фотону с энергией ћ w соответствует энергия mc 2
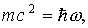
здесь с — скорость света.
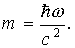
Учитывая, что импульс фотона p = mc, получим из (1.6)
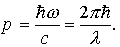
Здесь учтено соотношение между частотой света w и его длиной волны l :
Уравнение (1.7) связывает между собой длину волны света l — характеристику, связанную с его волновой природой и импульс фотона p, характеризующий его как частицу.
Заслуга де Бройля состоит в том, что он распространил формулу (1.7) на все частицы материи, придав ей универсальное значение. Согласно гипотезе де Бройля состояние частицы, движущейся в изотропной среде без влияния внешних сил, описывается волновой функцией, имеющей вид плоской монохроматической волны. Длина волны выражается формулой
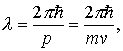
где импульс частицы p = mv (m — масса частицы, v — ее скорость).
Формула (1.8) соответствует равенству (1.7) для света и называется соотношением де Бройля. Для малых (нерелятивистских) скоростей масса частицы m соответствует ее массе покоя m0, для скоростей, близких к скорости света с:
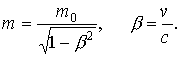
Подтверждением гипотезы де Бройля явились проведенные в 1927 г. опыты Девиссона и Джермера по наблюдению дифракции электронов, отраженных от кристаллов. Импульс электрона, ускоренного разностью потенциалов U, выражается формулой
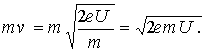
Тогда длина волны электрона
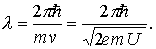
Подставляя в формулу (1.11) численные значения входящих в нее величин, получим
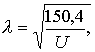
где напряжение U необходимо взять в вольтах. Тогда l выразиться в ангстремах (1 Å = 10 -10 м). Оказывается, что для электронов, ускоренных разностью потенциалов порядка сотен вольт, длина волны де Бройля составляет приблизительно 1 Å . Это значит, что обычные дифракционные решетки, используемые в оптике, непригодны для постановки опытов по дифракции электронов. Роль дифракционной решетки в этом случае, как и в случае рентгеновских лучей, могут выполнять монокристаллы.
1.3. Волновая функция свободного электрона. Статистический смысл волновой функции
Уравнение плоской волны имеет вид
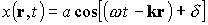
где x(r,t) — величина волнообразно распространяющегося возмущения (смещение точки от положения равновесия, напряженность электрического поля и др.); a — амплитуда волны; k — волновой вектор, совпадающий с направлением распространения волны, равный по модулю 2 p / l ; r — радиус-вектор, проведенный в произвольную точку плоскости равной фазы; w — круговая частота; t – время; d — начальная фаза.
Уравнение плоской волны часто представляют в виде комплексной
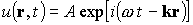
где величина волнообразно распространяющегося возмущения u(r,t) и амплитуда волны А — комплексные величины, причем, 
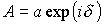
Уравнение (1.14) обладает тем свойством, что его действительная часть совпадает с уравнением (1.13):
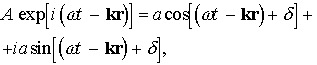
Комплексная амплитуда А объединяет в себе действительную амплитуду а и начальную фазу d . Отметим, что a = | A |.
В соответствии с гипотезой де Бройля, каждой свободной частице соответствует волна с частотой
и волновым вектором
Следовательно, для свободной частицы с не равной нулю массой покоя волновую функцию, которую принято обозначать Y (r,t), можно записать в виде:
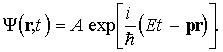
Волну, описываемую функцией вида (1.16), соответствующую свободной частице с энергией Е и импульсом p, называют волной де Бройля. Под Е в этих формулах понимают полную энергию частицы, смысл которой раскрывается в теории относительности.
Выясним физическую интерпретацию волновой функции Y (r,t). Очевидно, что с волной вида (1.16) нельзя связать частицу, т.к. частица локализована в пространстве, т.е. обладает вполне определенными значениями координат в определенный момент времени, а волна безгранична в пространстве. На первых этапах развития квантовой физики делались попытки представить частицу как суперпозицию волн. В силу математической теоремы Фурье из плоских волн с различными частотами и волновыми векторами можно составить волновой пакет, имеющий сколь угодно малое протяжение в пространстве. Групповая скорость волн де Бройля
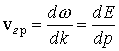
совпадает со скоростью частицы v. Эти попытки не привели к успеху, поскольку, как показывает детальный анализ, волновой пакет расплывается с течением времени в пространстве и, следовательно, не может характеризовать стабильную во времени частицу.
Нельзя принять и противоположную точку зрения, согласно которой волны распространяются в среде, состоящей из частиц, подобно, например, звуковым волнам. Такая точка зрения предполагает, что волновые свойства присущи только ансамблю из многих частиц, а не отдельным частицам. Этой точке зрения противоречат опыты, проведенные в 1948 году В.А. Фабрикантом, Л.В. Биберманом и Н.Г. Сушкиным. Они использовали настолько слабый пучок электронов, что интервал времени между пролетом каждого электрона в тысячи раз превышал время пролета электрона. В этом эксперименте исключалось влияние электронов друг на друга. При такой постановке опыта на экране, покрытом флюоресцирующим составом, появлялись отдельные точки — следы попадания электронов. При прохождении через дифракционную решетку большого числа электронов обнаруживалось, что эти точки не распределяются на экране равномерно, а группируются там, где в опытах с интенсивными электронами пучками располагаются дифракционные максимумы. В этих опытах, кроме доказательства того факта, что волновые свойства присущи отдельному электрону, отчетливо проявилось также свойство неделимости микрочастиц.
Анализ опытов по дифракции отдельных электронов показывает, что при точно заданной энергии движущихся электронов нельзя заранее предсказать в какую точку экрана попадет конкретный электрон. Можно лишь утверждать, что существует определенная вероятность попадания его в ту или иную точку экрана. Величина этой вероятности может быть оценена по плотности следов электронов в данном месте экрана после прохождения через прибор многих электронов.
Впервые вероятностное истолкование волновой функции было предложено М. Борном: интенсивность волны де Бройля в каком-либо месте пространства пропорциональна вероятности обнаружить частицу в этом месте. Поскольку интенсивность волны определяется квадратом ее амплитуды (для комплексных величин — квадратом модуля), то для плотности вероятности обнаружения частицы в различных местах пространства можно записать следующее выражение:
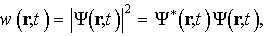
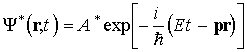
комплексно сопряженная функция.
Следует особо отметить, что комплексный характер волновой функции Y (r,t) имеет в квантовой физике принципиальное значение. Все физические величины, имеющие реальный физический смысл, выражаются через всю комплексную функцию Y (r,t), а не только через ее вещественную часть, как это принято в классической физике.
Используя определение плотности вероятности обнаружения частицы, можно определить вероятность нахождения частицы в любом объеме пространства V. Эта вероятность вычисляется с помощью одного из следующих интегралов:
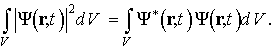
Интегрирование производится по всему объему V.
1.4. Соотношения неопределенностей Гейзенберга
Состояния классических частиц в ньютоновской механике и микрочастиц в квантовой физике описываются принципиально различными способами. В классической механике движение частицы описывается траекторией и в каждый момент времени частица имеет определенное положение и импульс. Поскольку микрочастицам присущи одновременно и корпускулярные и волновые свойства, то в квантовой физике в принципе нельзя говорить о траектории частицы, т.е. нельзя характеризовать мгновенное состояние микрочастицы точными заданиями ее положения и импульса.
В соответствии с гипотезой де Бройля любой частице одновременно присущи как корпускулярные, так и волновые свойства. Нетрудно убедиться, что эти два метода описания одних и тех же физических объектов во многом исключают друг друга. Например, не имеет смысла говорить о локализации монохроматической волны в пространстве, поскольку длина волны есть характеристика синусоиды, а синусоида — бесконечная периодическая кривая. Отсюда следует, что должны существовать принципиальные пределы применимости к микрочастицам понятий, характеризующих частицу в классической механике.
Заслуга в согласовании корпускулярных и волновых свойств микрообъектов принадлежит В. Гейзенбергу. Свои результаты он сформулировал в 1927 году в виде соотношений или принципа неопределенностей. Эти соотношения определяют принципиальный предел неточностей координат D x, D y, D z и соответствующих компонент импульса D px, D py, D pz, с которыми состояние частицы может характеризоваться классически:
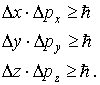
В соответствии с этими соотношениями следует, что чем точнее измерено положение частицы, тем с меньшей точностью можно характеризовать ее импульс, и наоборот. В частности, неопределенности импульса может и не быть ( D p x = 0), как в случае свободной частицы, характеризуемой плоской волной де Бройля. Но тогда D x = ¥ , т.е. о месте, где локализована микрочастица, ничего определенного сказать нельзя. Она с равной вероятностью может быть обнаружена в любой точке пространства. Если D x = 0, то D p x = ¥. В этом случае об импульсе можно высказать только вероятностное утверждение. Можно показать, что в этом случае все значения импульса равновероятны. Другими словами, если для микрочастицы точно известно ее положение в данный момент времени, то куда она будет двигаться в следующий момент времени ничего определенного сказать нельзя.
Проиллюстрируем на конкретных примерах, как с помощью соотношений неопределенностей Гейзенберга можно оценить пределы применимости к частицам понятий классической механики. Хорошо известно, что движение электрона в камере Вильсона, электронно-лучевой трубки осциллографа, кинескопа телевизора хорошо описывается законами ньютоновской механики. С другой стороны, тот же электрон в атоме водорода требует для описания своего состояния применения законов квантовой физики. Кажущееся противоречие легко объясняется с помощью количественных оценок в соответствии с соотношениями (1.21). Наблюдая трек электрона в камере Вильсона, можно лишь утверждать, что он прошел внутри капельки тумана, размер которой приблизительно 1 × 10 -6 м. Приняв это значение за неопределенность координаты электрона D x, получим для неопределенности скорости (м/с)
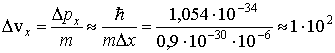
Типичные электроны, попадающие в камеру Вильсона, имеют скорости vx
1 × 10 7 м/с. Таким образом, D vx vx и неопределенность скорости не оказывает принципиального влияния на траекторию электрона.
Для электрона в атоме водорода D x
1 × 10 6 м/с. Оценки скорости электрона в атоме водорода в рамках классической механики приводят к значениям vx
1 × 10 6 м/с, т.е. в этом случае неопределенность скорости сравнима с самим значением скорости и говорить о каком-то определенном значении скорости электрона в атоме водорода не имеет смысла. Аналогичные результаты справедливы и для элементарных частиц при движении в очень малых областях пространства. Поэтому в квантовой физике при описании движений микрочастиц отказались от понятия траектории, поскольку такое понятие для этих физических объектов теряет смысл.
Оценим теперь неопределенность скорости для макроскопического тела, обладающего достаточно большой массой. Пусть это будет тело массой 1 г. Положение центра тяжести такого тела будем определять с точностью до размера атома ( D x = 1 × 10 -10 м). В этом случае

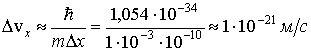
т.е. для макроскопических тел неопределенность скорости настолько мала, что находится за пределами доступных способов измерений. Поэтому соотношения неопределенностей для таких тел не играют никакой роли.
Рис.1.1. Определение положения электрона с помощью экрана со щелью
Соотношения неопределенностей Гейзенберга играют существенную роль в проблеме измерений в квантовой физике. Они устанавливают принципиальный предел точности измерений, который невозможно превзойти совершенствованием приборов и методов измерений. Любая попытка измерить, например, координату частицы приводит к искажению первоначального состояния частицы за счет взаимодействия ее с измерительным прибором, в результате чего появляется неопределенность в значении импульса. Простейшим экспериментальным прибором, позволяющим определить положение электрона, может служить узкая щель или отверстие, расположенные перпендикулярно направлению движения электрона (рис. 1.1). Направим ось x параллельно плоскости щели, а ось y — перпендикулярно к ней, как это показано на рисунке. Пусть импульс электрона до прохождения щели будет равен p, причем неопределенность x-составляющей импульса D px = 0. Если электрон прошел через щель, о чем может свидетельствовать сцинтилляция на флюоресцирующем экране Э, то его координата в момент прохождения через щель будет определена с точностью D x, равной ширине щели. После прохождения щели электрон вследствие явления дифракции имеет вероятность отклониться от первоначального направления движения и у него появится составляющая импульса px. Кривая на рис. 1.1 справа схематически описывает распределение вероятности попадания электрона на экран. Если через a обозначить угол, ограничивающий положение первого дифракционного максимума на экране, то
a согласно условию дифракции от щели
Из последних двух равенств получаем
что согласуется с соотношениями неопределенностей Гейзенберга.
В квантовой механике имеет место также соотношение неопределенностей Гейзенберга для времени и энергии:
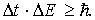
Это соотношение означает, что чем короче время существования какого-либо состояния или время, отведенное для его наблюдения, тем с меньшей определенностью можно говорить об энергии этого состояния. Наоборот, чем больше это время, тем с большей точностью определена энергия состояния. Отсюда следует, что стационарное состояние может существовать бесконечно. Из соотношения (1.22) вытекает возможность существования виртуальных частиц, которые существуют только в состояниях, имеющих малую длительность, и не могут быть зарегистрированы. Виртуальные частицы являются переносчиками взаимодействия. Например, два электрона взаимодействуют друг с другом путем испускания одним электроном и поглощения другим виртуального фотона.
1.5. Уравнение Шредингера
Волновая функция в виде плоской монохроматической волны описывает частный случай движения квантово-механической частицы — движение свободной частицы. Именно микрочастица, которая не подвергается какому-либо внешнему воздействию, описывается волной де Бройля. Возникает вопрос, какой вид будет иметь волновая функция и как ее найти, если частица не является свободной, находится, например, во внешнем поле? В классической физике существует уравнение, описывающее движение тела в самом общем случае — это основное уравнение динамики, второй закон Ньютона. В квантовой физике также существует уравнение, с помощью которого можно описать состояние микрочастицы в разнообразных условиях. Это уравнение называется уравнением Шредингера. Так же, как и уравнение Ньютона, уравнение Шредингера не выводится, его справедливость подтверждается многочисленными экспериментальными фактами, являющимися следствием этого уравнения.
Уравнение Шредингера — это дифференциальное уравнение, неизвестной в котором является волновая функция микрочастицы Y (r,t), зависящая в общем случае от координат и времени. В случае потенциальных силовых полей, описываемых потенциальной энергией U(r), общее уравнение Шредингера имеет вид
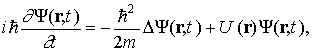
здесь i — мнимая единица; m — масса частицы; r — радиус-вектор, определяющий ее положение; D — оператор Лапласа, который в прямоугольной декартовой системе координат записывается в виде
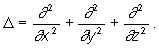
Волновая функция — комплексная величина и поэтому физического смысла не имеет. Но нахождение волновой функции в результате решения уравнения Шредингера позволяет вычислить наблюдаемую физическую величину — плотность вероятности или плотность распределения координат частицы w(r,t):
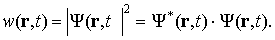
Вероятность обнаружения частицы в бесконечно малом элементе объема dV будет равна, очевидно, 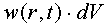
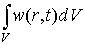
Таким образом, задача квантовой механики состоит в определении вероятностей тех или иных событий с помощью волновой функции, являющейся решением уравнения Шредингера. По вероятностям можно найти средние значения случайных физических величин, т.е. рассчитать те параметры, которые можно измерить.
Как любое линейное дифференциальное уравнение в частных производных уравнение Шредингера имеет множество решений. Причем, всякая линейная комбинация любых частных решений также является решением этого уравнения.
Среди решений уравнения Шредингера есть стационарные. Стационарными называются состояния, в которых ни одна из квантово-механических вероятностей не изменяется со временем. Для любого стационарного состояния волновую функцию можно записать в виде
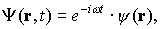
где функция 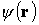
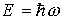
С учетом (1.26) уравнение Шредингера принимает вид
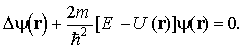
Уравнение (1.27) называется уравнением Шредингера для стационарных состояний или стационарным уравнением Шредингера. Волновая функция 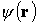
Потенциальная функция в уравнениях (1.23) и (1.27) определяется так же, как в классической физике, т.е. как потенциальная энергия точечной частицы, локализованной в некоторой точке силового поля, координаты которой определяются радиусом-вектором r.
Стационарное уравнение Шредингера необходимо дополнить граничными условиями, которые накладывают определенные условия на волновую функцию 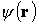
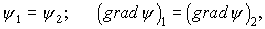
где индексы 1 и 2 соответствуют значениям функций на границе двух соседних областей.
1.6. Частица в одномерной прямоугольной потенциальной яме
Рис. 1.2. Одномерная прямоугольнаяпотенциальная яма
В этом и последующих разделах будут рассмотрены конкретные примеры решения некоторых наиболее важных квантово-механических задач, описывающих поведение микрочастиц в различных силовых полях. В качестве первого примера рассмотрим одномерную задачу о поведении микрочастицы, находящейся в силовом поле с распределением потенциальной энергии U(x), показанном на рис. 1.2. В этой задаче U(x) = 0 в области 0 ¥ вне этой области. Такая простая физическая задача может быть решена аналитически точно и на ее примере можно рассмотреть вопрос о квантовании энергии микрочастицы. С другой стороны, эта физическая модель имеет применение в некоторых реальных задачах ядерной физики и физики твердого тела.
Уравнение Шредингера в одномерном случае для частицы массой m внутри прямоугольной потенциальной ямы запишется в виде
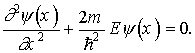
Будем искать общее решение уравнения (1.29) в виде
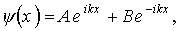
где k — некоторый действительный параметр, который будет определен в результате подстановки решения (1.30) в уравнение (1.29). Вычисляя вторую производную волновой функции и подставляя y( x) и ¶ 2 (x)/ ¶ x 2 в уравнение Шредингера (1.29), получим равенство, определяющее волновое число k через полную энергию микрочастицы Е:
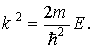
Следовательно, полная энергия микрочастицы в потенциальной яме определяется ее волновым числом и массой:
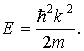
Рассмотрим теперь поведение волновой функции на границах потенциальной ямы. В классической физике частица с конечной энергией Е не может попасть в область, где потенциальная энергия бесконечна. В квантовой механике это соответствует требованию обращения в нуль в этой области плотности вероятности w и, следовательно, самой волновой функции y . В соответствии с этим требованием для нашей задачи на левой границе потенциальной ямы
Для правой границы (x=L)
Рис. 1.3. Энергия частицы в прямоугольной потенциальной яме
Согласно формуле Эйлера 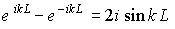
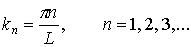
Следовательно, и энергия микрочастицы в потенциальной яме может принимать не любые, а строго определенные дискретные или квантованные значения:
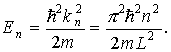
Энергетический спектр частицы в прямоугольной потенциальной яме схематически показан на рис. 1.3. Целое положительное число n, определяющее значение энергии частицы, называется квантовым числом. Необходимо отметить, что минимальная из возможных значений энергия частицы Е1 (n = 1) отлична от нуля. Этот результат вытекает также и из принципа неопределенностей Гейзенберга. Действительно, если бы микрочастица находилась в состоянии покоя, то она одновременно обладала бы определенными значениями координаты (x = const) и импульса p = 0, что противоречит соотношениям неопределенностей Гейзенберга.
Значения полной энергии микрочастицы En, для которых уравнение Шредингера имеет решения, называются собственными значениями энергии.
Оценим расстояние между соседними уровнями энергии для различных значений массы частицы m и ширины потенциальной ямы L. Разность энергий двух соседних уровней при n >> 1
Если взять m порядка массы молекулы (
10 -26 кг), а L порядка 10 см (молекула газа в сосуде), то разность энергий двух соседних стационарных состояний
где D En – разность энергий, Дж. Столь густо расположенные энергетические уровни молекулы будут восприниматься как сплошной спектр энергии.
Результат практически не изменится, если в качестве частицы взять электрон (m
10 -30 кг), оставив те же размеры потенциальной ямы. Этот случай соответствует свободному электрону в металле, электрону в электронно-лучевой трубке осциллографа и т.д.:
Такие разности энергии между соседними уровнями так же, как и в предыдущем примере недоступны для экспериментальных измерений.
Результат получится совсем другой, если область, в пределах которой может находиться электрон, будет порядка размеров атома (
10 -10 м). В этом случае
Дискретность энергетических уровней в этом случае весьма заметна.
Волновые функции, являющиеся решениями стационарного уравнения Шредингера для собственных значений энергии En называются собственными волновыми функциями. Как было показано выше, для частицы в прямоугольной потенциальной яме собственные волновые функции имеют вид
Константа С находится из условия нормировки волновой функции. Это условие соответствует очевидному утверждению, что вероятность обнаружить частицу в каком-либо месте потенциальной ямы, т.е. для интервала значений 0 £ x £ L, равна 1. Следовательно, условие нормировки в данном случае будет иметь вид
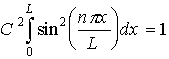
Интеграл в этом выражении, как известно, равен L/2, следовательно
Теперь можно в явном виде записать выражения для собственных функций частицы в одномерной прямоугольной потенциальной яме:
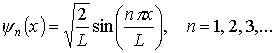
На рис. 1.4,а схематически показаны первые три собственные волновые функции для частицы в одномерной прямоугольной потенциальной яме. На рис. 1.4,б приведены соответствующие распределения плотности вероятности положения частицы в потенциальной яме:
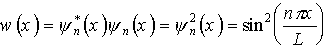
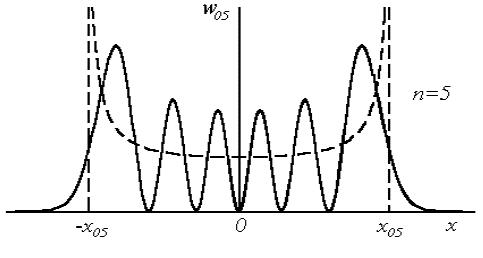
Рис. 1.4. Графики собственных волновых функций: а — плотностей вероятностей; б — для первых трех значений квантового числа
1.7. Квантовый гармонический осциллятор
Осциллятором называют физическую систему, совершающую колебания. Если колебания описываются синусоидальной функцией, то такой осциллятор называется гармоническим. Примерами классических осцилляторов могут служить математический маятник, груз на пружине и т.д. Движение этих осцилляторов происходит под действием квазиупругой силы 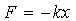
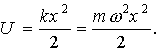
Понятие осциллятора применяется также к немеханическим колебательным системам. В частности, электрический колебательный контур является электрическим осциллятором.
В квантовой механике понятие силы не используется. Поэтому аналогом классического осциллятора в квантовой физике будет квантовый гармонический осциллятор, состояние которого описывается уравнением Шредингера с потенциальной функцией вида (1.36). Такие квантовые колебания совершают атомы в молекулах, ионы в узлах кристаллической решетки твердого тела (фононы), валентные электроны в твердых телах относительно ионного остова (плазмоны) и др.
Стационарное уравнение Шредингера для одномерного случая (линейный гармонический осциллятор) имеет вид

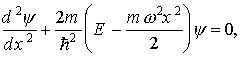
здесь, как обычно в квантовой механике, Е — полная энергия квантового осциллятора.
Уравнение (1.37) имеет решения только при значениях энергии Еn, равных
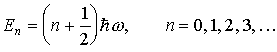
Энергетические уровни квантового гармонического осциллятора эквидистантны, т.е. находятся на равных расстояниях друг от друга (рис. 1.5). На этом рисунке через ±x0n обозначены точки поворота классического осциллятора с такой же энергией En, как и у квантового осциллятора.
Рис. 1.5. Схема энергетических уровней квантового гармонического осциллятора
Таким образом, полная энергия квантового гармонического осциллятора может принимать только определенные дискретные значения. Наименьшее воз-можное значение энергии 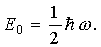
Собственные волновые функции квантового гармонического осциллятора могут быть представлены в виде
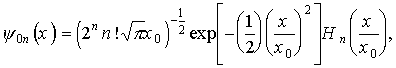
где 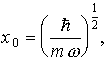
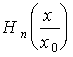
Полиномы Чебышева-Эрмита низших степеней имеют вид
Из свойств полиномов Чебышева-Эрмита следует, что все их корни некратные и вещественные. Число корней полинома равно его степени n, в чем легко убедиться, анализируя приведенные выше выражения для полиномов низших степеней. На рис. 1.6 приведены распределения плотности вероятности 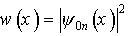
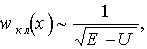
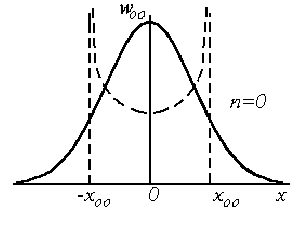
При малых n, что соответствует низшим энергетическим состояниям, квантовый и классический осцилляторы существенно ведут себя по разному. Однако, при достаточно больших энергиях функция 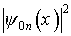
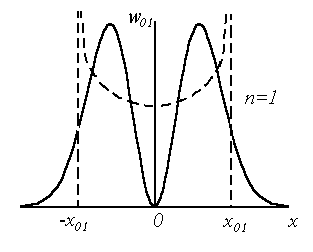
Рис.1.6. Распределение плотности вероятности для трех состояний квантового гармонического осциллятора
Отметим еще одну особенность квантово-механического осциллятора. Как видно из рис. 1.6, вероятность обнаружить микрочастицу, совершающую квантово-механические колебания вне пределов, ограничивающих движение классического осциллятора, не равна нулю. Такое поведение квантово-механического осциллятора связано с более общим свойством микрочастиц проникать за пределы потенциальных барьеров, недоступных с точки зрения классической физики. Эта проблема будет подробно рассмотрена в следующем разделе.
1.8. Прохождение частиц через потенциальный барьер.
Рис. 1.7. Потенциальный барьер конечной ширины
Рассмотрим поведение квантово-механической частицы при прохождении через потенциальный барьер конечной ширины (рис.1.7). Ограничимся рассмотрением одномерной задачи, когда ось x параллельна движению частицы. В каждой из трех областей I, II и III потенциальная энергия микрочастицы постоянна, но при переходе из одной области в другую меняется скачком. Эта задача моделирует многие физически важные явления, например, выход электронов из металлов, распад атомных ядер и др.
Уравнение Шредингера в этом случае будет иметь вид
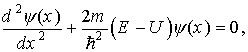
где потенциальная энергия

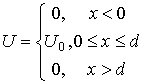
E — полная энергия частицы.
В области I уравнение (1.40) будет иметь вид
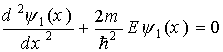
Частное решение уравнения (1.41) будем искать в виде волны, распространяющейся вдоль положительного направления оси x:
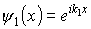
Подставляя (1.42) в (1.41), получим
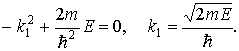
Общее решение уравнения (1.41) для области I представляет собой суперпозицию плоских волн, распространяющихся в противоположных направлениях оси x:
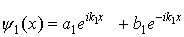
Для области II уравнение Шредингера запишется в виде
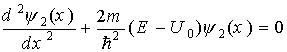
Общее решение этого уравнения будет иметь вид
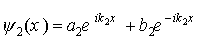
где волновое число в области II
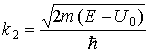
Уравнение Шредингера для микрочастицы в области III будет иметь тот же вид, что и в области I. Общее решение для этой области будет отличаться от решения (1.44) тем, что в области III нет отраженной волны (b3 = 0)
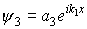
Для вычисления коэффициентов a1, b1, a2, b2 и a3 воспользуемся граничными условиями, согласно которым на границах областей волновая функция и ее первая производная должны быть непрерывны.
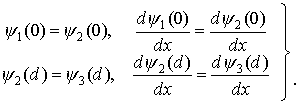
Для простоты вычислений можно положить a1=1, т.к. все коэффициенты b1, a2, b2 и a3 можно, не изменяя общности задачи, разделить на a1. Тогда из условий (1.49) получим систему алгебраических уравнений относительно неизвестных b1, a2, b2 и a3
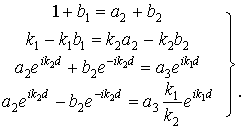
В случае, когда энергия частицы меньше высоты потенциального барьера (E = ik, где
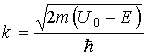
Вероятность обнаружить частицу за потенциальным барьером (в области III) равна квадрату модуля амплитуды, прошедшей в эту область волны: D = |a3| 2 = = a3a3 * . Величину D называют коэффициентом прозрачности барьера.
Решая систему уравнений (1.50) с учетом граничных условий (1.49), получим следующее выражение для коэффициента прозрачности:
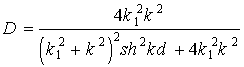
Формулу (1.51) можно значительно упростить, если положить
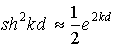
что для реальных ситуаций справедливо, и пренебречь слагаемыми, значительно меньшими, чем экспонента. Тогда
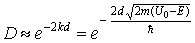
Отсюда видно, что проницаемость барьера сильно зависит от ширины барьера d и величины U0 — E.
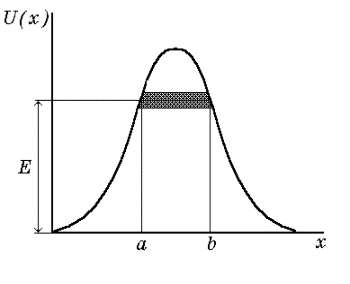
В случае потенциального барьера произвольной формы (рис. 1.8) проницаемость барьера выражается приближенной формулой
Рис. 1.8. Потенциальный барьер произвольной формы
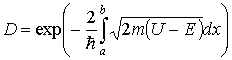
которая, как нетрудно увидеть, является обобщением формулы (1.52).
Таким образом, квантово-механической частице для преодоления потенциального барьера необязательно иметь энергию больше, чем высота барьера. Она как бы проходит через “туннель” (заштрихованная область на рис. 1.8), расположенном на высоте E, где E — полная энергия микрочастицы. В связи с этим рассмотренное явление называют туннельным эффектом.
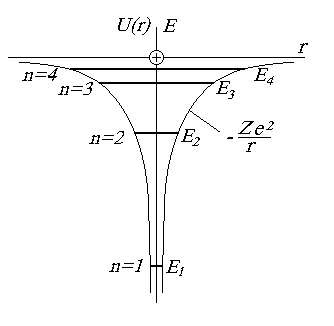
1.9. Водородоподобные атомы
Атомы, содержащие один внешний электрон называются водородоподобными. Потенциальная энергия электрона в таких атомах определяется сферически симметричным полем взаимодействия его с ядром (рис. 1.9):
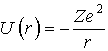
где Z — зарядовое число атома, r — расстояние электрона от ядра.
Для электрона, связанного с атомом, E 0).
Уравнение Шредингера для электрона в атоме имеет вид
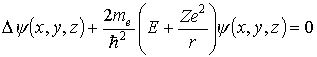
В сферической системе координат уравнение (1.55) преобразуется к виду
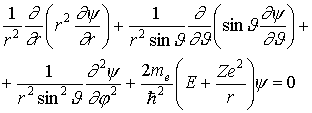
где 
Рис. 1.9. Энергетическая диаграмма водородоподобного атома
Для E 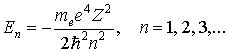
Собственные функции, удовлетворяющие уравнению (1.56), зависят от трех целочисленных параметров n, l и m:
Параметр n называется главным квантовым числом и определяет полную энергию электрона в атоме (см. формулу (1.57)). Этим числом обозначают номер энергетического уровня электрона в атоме (рис. 1.9).
Параметр l определяет модуль момента импульса электрона в атоме:
и называется азимутальным или орбитальным квантовым числом. При данном главном квантовом числе n квантовое число l может принимать n различных значений от 0 до n-1.
Параметр m определяет величину проекции момента импульса на некоторое направление z
Этот параметр называется магнитным квантовым числом.
Таким образом, каждому значению энергии электрона в атоме соответствует несколько состояний, отличающихся квантовыми числами l и m, и собственными волновыми функциями 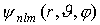
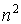
Волновая функция 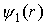
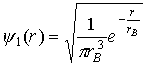
где 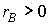
Функция 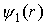
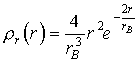
На рис. 1.10 представлен график функции 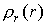
Для полного описания состояния электрона в атоме необходимо к трем квантовым числам n, l, m добавить еще одно — спиновое квантовое число (спин) S. Это квантовое число определяет ориентацию собственного момента количества движения электрона на некоторое направление, например, на направление орбитального момента электрона. Квантовое число S может принимать только два значения: 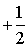
Рис. 1.10. График функции 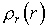
http://helpiks.org/6-65832.html
http://sibsauktf.ru/courses/foet/Foet_1.htm