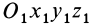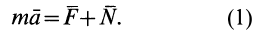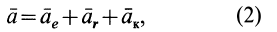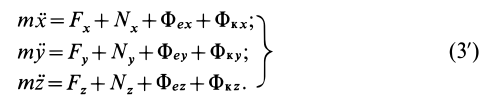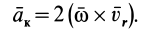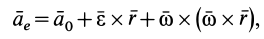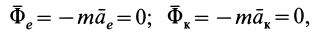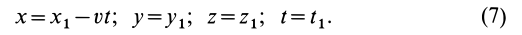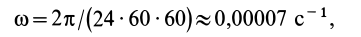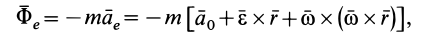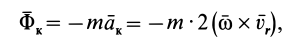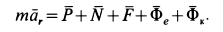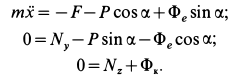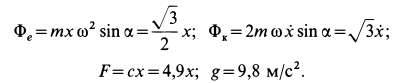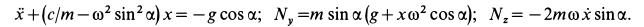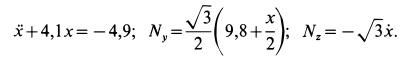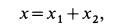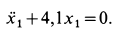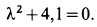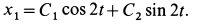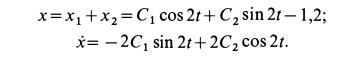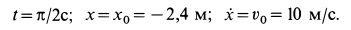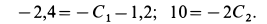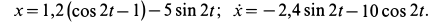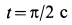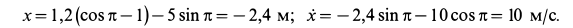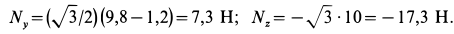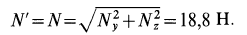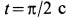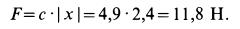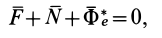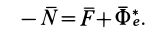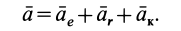Относительное движение материальной точки в теоретической механике
Содержание:
Относительное движение материальной точки:
Во многих задачах динамики рассматривается движение материальной точки относительно системы отсчета, движущейся относительно инерциальной системы. Дифференциальные уравнения движения материальной точки относительно таких подвижных, в общем случае неинерциальных, систем отсчета получают из уравнений движения точки относительно инерциальной системы отсчета и кинематической теоремы Кориолиса о сложении ускорений.
Имеем инерциальную систему отсчета
Рис. 14
Если ввести другую, неинерциальную, систему отсчета 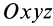
где 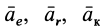
Подставляя значение абсолютного ускорения 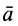
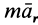
где 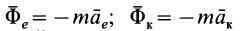
Силы инерции 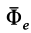
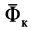
Если координаты движущейся точки относительно подвижной системы координат 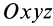
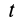
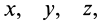
Это дифференциальные уравнения движения точки относительно подвижной системы координат в проекциях на декартовы подвижные оси координат. Они отличаются от дифференциальных уравнений абсолютного движения относительно инерциальной системы отсчета только наличием поправок на неинерциальность системы отсчета.
Относительное движение по инерции
Если материальная точка движется относительно подвижной системы отсчета прямолинейно и равномерно, то такое движение называют относительным движением по инерции. В этом случае относительная скорость 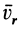
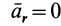
Это условие для сил при относительном движении точки по инерции.
Относительное равновесие
При покое материальной точки относительно подвижной системы отсчета ее относительные скорость и ускорение равны нулю, т. е. 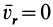
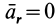
Из (3) получаем условие относительного равновесия для сил:
При абсолютном движении по инерции или абсолютном равновесии относительно инерциальной системы отсчета имеем для сил одно и то же условие 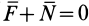
Инерциальные системы отсчета
Переносное ускорение в общем случае вычисляется по формуле
где 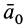
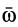
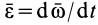
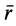
Пусть подвижная система отсчета все время движется относительно основной инерциальной системы поступательно, равномерно и прямолинейно. В этом случае переносная и кориолисова силы инерции равны нулю, т. е.
так как при поступательном движении 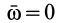
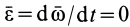
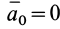
которое совпадает с уравнением движения относительно инерциальной системы отсчета (1).
Все подвижные системы отсчета, которые движутся поступательно, равномерно и прямолинейно относительно основной инерциальной системы отсчета, называются тоже инерциальными. Относительно всех инерциальных систем отсчета получаются одинаковые уравнения движения материальной точки. Ускорения материальной точки относительно всех инерциальных систем отсчета одинаковы.
Отсутствие принципиальной возможности каким-либо механическим опытом, основанным на наблюдении за движением материальных тел, отличить одну инерциальную систему отсчета от другой находится в основе принципа относительности классической механики — принципа Галилея — Ньютона, который утверждает: все механические явления в различных инерциальных системах отсчета протекают одинаково, или никаким механическим опытом нельзя обнаружить инерциальное движение системы отсчета, участвуя вместе с ней в этом движении. Наоборот, неинерциальную систему отсчета можно обнаружить и отличить одну от другой по поправкам на неинерциальность.
Скорости материальной точки относительно различных инерциальных систем отсчета разные, но нет возможности из наблюдений за движением материальной точки в различных системах отсчета сделать утверждение, какая из инерциальных систем отсчета является основной, неподвижной, а какая — подвижной.
В специальной теории относительности имеет место принцип относительности Эйнштейна, который утверждает: все физические явления во всех инерциальных системах отсчета протекают одинаково. Физические явления кроме механических включают также электромагнитные процессы.
Рис. 15
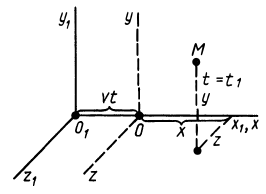
Возьмем две инерциальные системы отсчета: 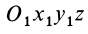
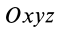
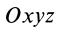
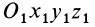
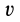
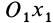
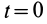
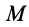
Эти соотношения называются преобразованиями Галилея в частном случае движения двух инерциальных систем отсчета друг относительно друга.
Преобразования Галилея не изменяют формы уравнения движения точки (1), т. е. оно инвариантно по отношению к преобразованиям Галилея.
Движение точки относительно земли
Для неинерциальной системы отсчета уравнение движения материальной точки под действием силы отличается от уравнения движения относительно инерциальных систем отсчета. Согласно (3), оно имеет форму
Наличие поправок на неинерциальность систем отсчета в виде сил инерции 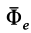
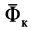
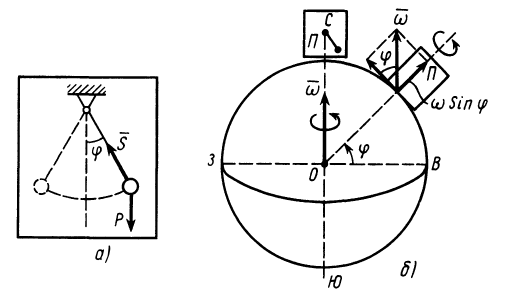
Система отсчета, скрепленная с земным шаром, не является инерциальной. Земной шар движется относительно гелиоцентрической инерциальной системы отсчета. При рассмотрении движения материальных тел относительно Земли должны проявлять себя эффекты, связанные с неинерциальностью системы отсчета. Земной шар движется относительно гелиоцентрической системы отсчета как свободное твердое тело. Его центр перемещается по эллиптической орбите, близкой к окружности. Кроме того, он вращается вокруг оси, проходящей через его центр, с почти постоянной по модулю и направлению угловой скоростью, совершая один оборот за сутки. Угловая скорость вращения Земли
т. е. величина малая по сравнению с единицей.
В общем случае переносная сила инерции
где 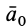
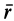
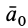
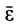
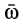
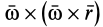
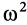
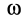
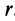
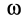
где 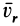
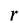
Маятник Фуко
Если подвесить на длинной нити груз достаточно малых размеров, то действующая на него сила 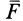
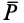
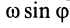
Рис. 16
Рис. 17
Если тело маятника имеет выступ, который при колебаниях может оставлять след, например на песке, то этот след при движении маятника в одну сторону будет отличаться от следа при движении в противоположную сторону из-за вращения Земли. Это отличие тем больше, чем длиннее нить маятника. Фуко в 1857 г. использовал маятник длиной 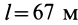
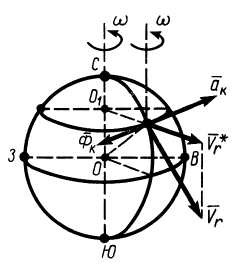
Отклонение движущихся тел вправо в Северном полушарии
В Северном полушарии из-за дополнительного действия силы инерции Кориолиса, вызванной вращением Земли, все движущиеся тела должны смещаться в правую сторону, если смотреть в направлении движения. Пусть материальная точка движется со скоростью 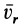
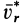
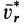
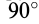
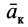
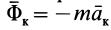
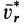
Если рассмотреть поступательное движение железнодорожного вагона, то для него сила инерции Кориолиса пройдет через центр его тяжести слева направо, если смотреть по движению вагона. Это приведет к увеличению давления на правый рельс и к его уменьшению на левый. На двухколейных железных дорогах правый рельс изнашивается быстрее левого.
Для частички воды в реке действие силы Кориолиса слева направо, если смотреть по течению реки, приведет к прижиманию этой частички к правому берегу, способствуя большему его подмыванию. Правый берег рек в Северном полушарии более подмыт, чем левый на прямолинейных участках реки. Этот эффект известен в географии как закон Бэра. На закруглениях реки вследствие центробежных сил инерции может оказаться подмытым и левый берег.
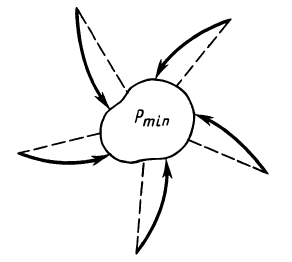
Действие силы инерции Кориолиса на летящие самолеты, ракеты, снаряды, движущийся воздух, морские течения приводит к их отклонению в правую сторону в Северном полушарии. В Южном полушарии отклонение будет в левую сторону. Сила инерции Кориолиса способствует образованию циклонов, антициклонов, вихрей, смерчей и т. д. Если в каком-то месте образовалось пониженное давление, например вследствие местного нагревания воздуха, то к этому месту начнет двигаться воздух из мест с повышенным давлением. Сила инерции Кориолиса отклонит движущиеся частички воздуха вправо, создав местный вихрь (рис. 18), а для больших масс воздуха— циклон. Аналогично, в местах с повышенным давлением образуются антициклоны.
Отклонение падающих тел к востоку
Рассмотрим в Северном полушарии тело, падающее вертикально вниз под действием силы тяжести без начальной скорости. Действие силы инерции Кориолиса в этом случае в первом приближении сведется к отклонению падающего тела к востоку. Действительно, если скорость тела 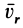
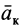
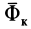
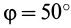
Пример:
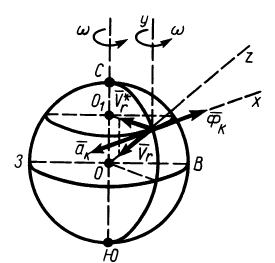
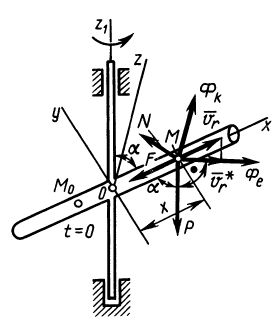
Внутри трубки, имеющей гладкую поверхность, находится шарик массой 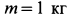
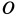
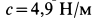
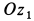
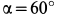
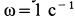
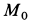
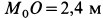
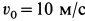
Определить закон движения шарика по трубке, принимая его за точку; силу давления шарика на стенку трубки и силу притяжения в момент времени 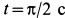
Решение:
Выберем систему подвижных осей координат 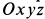
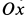
Векторное уравнение движения шарика относительно подвижной системы координат имеет вид
В проекциях на подвижные оси координат
Здесь 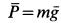
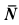
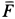
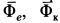
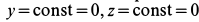
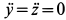
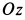
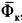
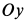
Подставляя эти значения сначала в общем виде в уравнения движения, после простых преобразований получаем:
После подстановки числовых значений величин имеем
Дифференциальное уравнение является линейным неоднородным; следовательно, его решение
где 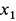
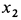
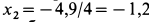
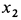
Общее решение однородного уравнения 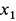
Его характеристическое уравнение
Корни характеристического уравнения 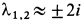
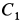
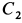
Начальные условия задачи
Подставляя их в выражения для 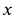
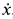
Их решения 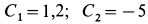
Уравнения движения шарика с учетом значений постоянных принимает вид
В момент времени
Подставляя эти значения 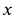
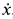
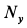
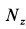
Давление шарика 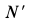
Сила притяжения 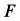
Невесомость
Динамическая теорема Кориолиса позволяет рассмотреть состояние невесомости, которое, в частности, возникает при движении космических кораблей как искусственных спутников Земли. При рассмотрении невесомости материальной точки целесообразно ее представлять как твердое тело, имеющее поверхность, которой оно может соприкасаться с другими телами. Будем предполагать, что скорости и ускорения всех точек тела одинаковы, а реакции соприкасающихся тел приводятся к равнодействующей.
Под невесомостью такой материальной точки понимают отсутствие давления этой точки на каждое из тел, с которым она может соприкасаться. В частности, невесомая материальная точка не давит на площадку весов (не имеет веса), находящихся в покое по отношению к той системе отсчета, относительно которой покоится материальная точка.
Систему отсчета, относительно которой материальная точка находится в покое и, следовательно, имеет относительно нее скорость и ускорение, равные нулю, назовем собственной системой отсчета материальной точки. Все величины относительно этой системы отсчета условимся обозначать специальным индексом 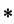
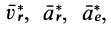
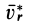
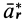
Невесомая материальная точка (тело), прикрепленная на пружине к любому телу, покоящемуся относительно ее собственной системы отсчета, не деформирует эту пружину. Учитывая, что давление точки на какое-либо тело по модулю совпадает с силой реакции тела на эту точку, невесомость наблюдается при равенстве нулю силы реакции от любого тела, соприкасающегося с рассматриваемой невесомой материальной точкой.
Если в общем случае рассматривать невесомость материального тела, а не точки, то реакции окружающих его тел сведутся к распределенным силам по поверхности его соприкосновения с этими телами. Сила реакции, отнесенная к единице площади поверхности соприкосновения (напряжение силы реакции), должна при невесомости тела быть равна нулю в каждой точке его поверхности. Это является условием невесомости для любого тела, не обязательно твердого.
Для абсолютно твердого тела при его невесомости вместо равенства нулю напряжения поверхностной силы в каждой точке его поверхности соприкосновения достаточно равенства нулю главного вектора и главного момента этих сил относительно любого центра приведения.
Ограничимся рассмотрением невесомости материальной точки, т. е. абсолютно твердого тела, для которого все поверхностные силы приводятся только к одной равнодействующей силе — реакции тел, соприкасающихся с ним. Невесомость материальной точки не связана с системой отсчета или с наблюдателем, находящимся в той или иной системе отсчета. Но для выявления сил, действие которых испытывает материальная точка, выберем ее собственную систему отсчета, по отношению к которой ее относительные скорость и ускорение равны нулю, т. е. 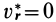
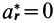
где 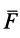
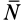
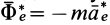
Из условия относительного равновесия сил имеем
Согласно определению невесомости, 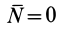
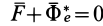
Таким образом, условие невесомости через силы можно выразить как 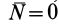
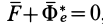
Согласно теореме о сложении ускорений, абсолютное ускорение в общем случае определяется по формуле
Если абсолютное ускорение рассматривать относительно инерциальной системы отсчета, а в качестве подвижной системы отсчета выбрать собственную систему отсчета, то 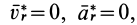
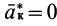
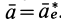
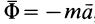
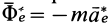
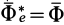
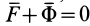
Проверим выполнение условия невесомости для материальной точки, находящейся в космическом корабле, который движется поступательно относительно Земли в качестве ее искусственного спутника за пределами атмосферы. За инерциальную систему отсчета можно принять систему отсчета, скрепленную с Землей.
Пусть материальная точка неподвижна относительно космического корабля. Тогда собственной системой отсчета будет система отсчета, скрепленная с кораблем. Силой от действия тел, не соприкасающихся с точкой, является сила тяготения Земли 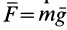
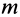
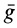
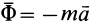
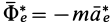
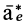
Если корабль не испытывает действия других сил, кроме силы тяготения Земли, то его ускорение от этого тяготения тоже равно 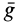
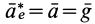
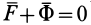
В космическом корабле, который кроме поступательного движения имеет также и вращение, каждая из материальных частиц корабля не находится в состоянии невесомости, хотя весь корабль как целое находится в состоянии невесомости. Для него главный вектор и главный момент поверхностных сил равны нулю, так как нет тел, с которыми корабль соприкасается своей поверхностью.
Материальная точка внутри кабины корабля находится в состоянии невесомости, пока она не соприкасается со стенками корабля и с другими телами, скрепленными с кораблем.
Кажется, что для невесомости тела необходима невесомость каждой его точки. Это приводит к требованию отсутствия взаимных давлений между точками тела или к отсутствию внутренних напряжений в теле. Но такие напряжения всегда имеются при невесомости вследствие естественной связи точек тела друг с другом, на которую можно влиять, например, термообработкой, изменением температуры и т. д. При невесомости тела как целого не обязательно отсутствие даже дополнительных напряжений, создаваемых движением тела. Достаточно равенства нулю напряжений в точках поверхности тела, создаваемых другими, соприкасающимися телами (связями), а для абсолютно твердого тела — равенства нулю главного вектора и главного момента поверхностных сил.
В невесомости находятся земной шар и другие планеты Солнечной системы, их спутники, если пренебречь действием на них метеоритов, космического излучения и т. д.
В состоянии невесомости находилось бы свободно падающее тело вблизи Земли, если бы не было действия воздуха. Невесомость можно создать искусственно вблизи Земли в герметизированной кабине летательного аппарата, заставив его с помощью двигателей совершать поступательное движение с ускорением 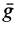
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Геометрия масс
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Переносная и кориолисова силы инерции
Два первых закона классической механики и полученные на их основе уравнения справедливы при движении точки в инерциальной системе отсчёта (ИСО). Существует ряд технических задач, в которых рассматривают движение материальной точки в подвижной системе отсчёта (ПСО), которая в общем случае не является инерциальной.
Инерциальная система отсчёта – система отсчёта, по отношению к которой изолированная материальная точка находится в покое или движется равномерно и прямолинейно.
Система отсчёта, не обладающая этим свойством, называется неинерциальной системой отсчёта
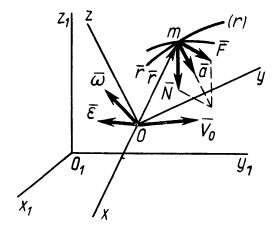
Рассмотрим движение материальной точки под действием активных сил Fi Е и реакций Ri Е относительно подвижной неинерциальной системы отсчёта OXYZ (рис. 3.1).
Напомним некоторые понятия кинематики, используемые в данном разделе динамики точки.
Движение точки по отношению к неподвижной системе отсчёта O1X1Y1Z1 называется абсолютным и характеризуется абсолютной скоростьюV и абсолютным ускорениемa. Положение точки на траектории абсолютного движения определяется тремя зависящими от времени координатами, которые называются уравнениями абсолютного движения:
Неподвижная система отсчёта O1X1Y1Z1 является инерциальной. В этой системе отсчёта основное уравнение динамики имеет вид
m·a = ΣFi Е + ΣRi Е ,
где Fi Е – активная сила; Ri Е – реакция внешней связи.
 |
Движение точки по отношению к подвижной системе отсчёта OXYZ называется относительным и характеризуется относительной скоростью Vr и относительным ускорением ar. Положение точки на траектории относительного движения определяется тремя зависящими от времени координатами, которые называются уравнениями относительного движения:
Подвижная система отсчёта OXYZ не является инерциальной. Применение в чистом виде первого и второго законов классической механики в ПСО неправомерно.
Рассмотрим переносное движение точки (рис. 3.2) и напомним суть некоторых понятий кинематики, используемых в этом разделе динамики.
Если координаты точки в ПСО постоянны (Х = C1 = const; Y = C2 = const; Z = C3 = const), то движение этой точки вместе с ПСО по отношению к неподвижной системе отсчёта называют переносным движением. Это движение характеризуется переносной скоростьюVe и переносным ускорениемae. Положение точки на траектории переносного движения определяется тремя зависящими от времени координатами, которые называют уравнениями переносного движения:
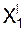
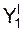
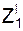
 |
Из курса кинематики известно, что абсолютное ускорение a точки определяют по формуле
a = ar + ae + ac,
где ar – относительное ускорение; ae – переносное ускорение; ac – ускорение Кориолиса.
Ускорение Кориолиса определяют по формуле
ac = 2( 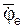
где 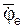
Модуль кориолисова ускорения находят по формуле
ac = 2ωe·Vr·sin( 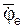
где ωе = I 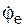
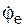
Кориолисово ускорение равно нулю в трех случаях:
1) если ωe = 0, т. е. в случае поступательного переносного движения или в момент обращения в нуль угловой скорости 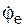
2) если Vr = 0, т. е. в случае относительного покоя точки или в момент равенства нулю относительной скорости движущейся точки;
3) если sin( 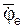
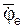
Направление кориолисова ускорения определяется по правилу векторного произведения. Согласно этому правилу вектор ac одновременно перпендикулярен векторам 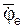
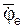
Направление ускорения Кориолиса находят также по правилу Жуковского: для определения направления ускорения Кориолиса необходимо относительную скорость Vr точки спроецировать на плоскость, перпендикулярную оси вращения, и повернуть эту проекцию в той же плоскости на угол 90 о в сторону переносного вращения.
Если подставим абсолютное ускорение a = ar + ae + ac в основное уравнение динамики точки m·a = ΣFi Е + ΣRi Е , то получим
m·(ar + ae + ac) = ΣFi Е + ΣRi Е .
Разрешим это уравнение относительно m·ar:
m·ar = ΣFi Е + ΣRi Е – m·ae – m·ac.
Введём два вектора: Фе = – m·ae; Фс = – m·ac. Эти векторы назовем переносной и кориолисовой силами инерции.
При исследовании движения механических систем в теоретической механике используют следующие понятия.
Сила инерции – величина, равная произведению массы материальной точки на её ускорение и направленная противоположно этому ускорению.
Переносная сила инерции при рассмотрении движения материальной точки в неинерциальной системе отсчёта – величина, равная произведению массы точки на её переносное ускорение и направленная противоположно этому ускорению.
Кориолисова сила инерции при рассмотрении движения точки в неинерциальной системе отсчёта – величина, равная произведению массы точки на её кориолисово ускорение и направленная противоположно этому ускорению.
Используя понятия переносной и кориолисовой сил инерции, получим
m·ar = ΣFi Е + ΣRi Е + Фе + Фс.
Последнее выражение называют дифференциальным уравнением относительного движения точки в векторной форме или основным уравнением динамики относительного движения.
Произведение массы m точки на её относительное ускорение ar равно геометрической сумме активных сил Fi Е , реакций внешних связей Ri Е , переносной силы инерции Фе и кориолисовой силы инерции Фс.
Проецируя последнее векторное равенство на координатные оси ПСО, получим дифференциальные уравнения относительного движения точки:
m· 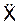
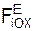
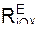
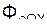
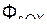
m· 


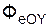
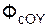
m· 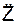


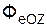
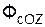
Произведение массы точки на проекцию её относительного ускорения на координатную ось ПСО равно сумме проекций активных сил, реакций внешних связей и переносной и кориолисовой сил инерции на ту же ось.

Силы инерции Фе, Фс направлены противоположно ускорениям ae, ac (рис. 3.3).
Дифференциальные уравнения относительного движения точки
m· 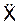


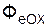
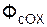
m· 


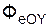
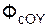
m· 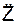


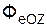
отличаются от дифференциальных уравнений движения точки в инерциальной системе отсчёта (см. раздел 1)
m· 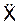


m· 


m· 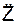

наличием в правой части этих уравнений проекций на соответствующие координатные оси переносной и кориолисовой сил инерции.
Уравнение относительного движения силы инерции
Силы инерции и основной закон механики
Берников Василий Русланович,
Внутренние силы в ряде случаев являются причиной появления внешних сил, приложенных к системе [3, с.197-202], [9, с.139-142], [10, с.364], [11, с.28-41]. Силы инерции всегда являются внешними по отношению к любой движущейся системе материальных тел [2, с.359], [4, с.189], [12, с.105], [13, с.218]. Силы инерции действуют также как и силы взаимодействия, они вполне реальны, могут совершать работу, сообщать ускорение [4, с.172], [10, с.280], [13, с.218], [14, с.95]. При большом количестве теоретических предпосылок в механике о возможности использования сил инерции в качестве поступательной при создании конструкций не приводили к положительному результату. Можно отметить только некоторые широко известные конструкции с небольшой эффективностью использования сил инерции: инерцоид Толчина [15], вихревой жидкостный движитель Фролова [16, с.63-68], движитель Торнсона [20, с.218-219]. Медленное развитие инерционных движителей объясняется отсутствием фундаментального теоретического обоснования наблюдаемого эффекта. На основании обычных классических представлений физической механики в данной работе создана теоретическая база использования сил инерции в качестве поступательной.
§1. Основной закон механики и его следствия.
Я страстная и распутная, работаю индивидуально, есть моя любимая подружка.
Рассмотрим законы преобразования сил и ускорений в различных системах отсчёта. Выберем произвольно неподвижную инерциальную систему отсчёта и условимся движение относительно неё считать абсолютным. В такой системе отсчёта основным уравнением движения материальной точки является уравнение, выражающее второй закон Ньютона.
где F – сила взаимодействия тел.
Тело, покоящееся в движущейся системе отсчёта, увлекается последней в её движении относительно неподвижной системы отсчёта. Такое движение называется переносным. Движение тела относительно системы отсчёта называется относительным. Абсолютное движение тела складывается из его относительного и переносного движений. В неинерциальных системах отсчёта ( системы отсчёта, движущиеся с ускорением) закон преобразования ускорений для поступательного движения имеет следующий вид
Учитывая (1.1) для сил запишем уравнение относительного движения для материальной точки в движущейся с поступательным ускорением системе отсчёта
где mwпер — это поступательная сила инерции, возникающая не из-за взаимодействия тел, а из-за ускоренного движения системы отсчёта. Движение тел под действием сил инерции аналогично движению во внешних силовых полях [ 2,с.359 ] . Импульс центра масс системы [ 3, с.198 ] может быть изменён путём изменения внутреннего вращательного импульса или внутреннего поступательного импульса. Силы инерции всегда являются внешними [ 2,с.359 ] по отношению к любой движущейся системе материальных тел.
Допустим теперь, что система отсчёта движется совершенно произвольно относительно неподвижной системы отсчёта. Это движение можно разделить на два: поступательное движение со скоростью vо, равной скорости движения начала координат, и вращательное движение вокруг мгновенной оси, проходящей через это начало. Угловую скорость этого вращения обозначим w , а расстояние от начала координат движущейся системы отсчёта до движущейся точки в ней через r. Кроме того, движущаяся точка имеет относительно движущейся системы отсчёта скорость vотн . Тогда для абсолютного ускорения [ 2,с.362 ] известно соотношение
где r ^ — компонента радиуса-вектора r, перпендикулярная к мгновенной оси вращения. Перенесём относительное ускорение в левую часть, а абсолютное в правую часть и всё умножим на массу тела, получим основное уравнение сил относительного движения [ 2,с.364 ] материальной точки в произвольно движущейся системе отсчёта
где: F – сила взаимодействия тел; Fк – кориолисова сила инерции; Fп – поступательная сила инерции; Fц – центробежная сила инерции; Fф – фазовая сила инерции.
Направление силы взаимодействия тел F совпадает с направлением ускорения тела. Кориолисова сила инерции Fк направлена согласно векторному произведению радиальной и угловой скорости, то есть перпендикулярно обоим векторам. Поступательная сила инерции Fп направлена противоположно ускорению тела. Центробежная сила инерции Fц направлена по радиусу от центра вращения тела. Фазовая сила инерции Fф направлена противоположно векторному произведению углового ускорения и радиуса от центра вращения перпендикулярно этим векторам.
Таким образом, достаточно знать величину и направление действия сил инерции и взаимодействия, чтобы определить траекторию движения тела относительно любой системы отсчёта.
Кроме сил инерции и взаимодействия тел существуют силы переменной массы, являющиеся следствием действия сил инерции. Рассмотрим второй закон Ньютона в дифференциальной форме [ 2, с.77 ]
где: P – импульс системы тел; ∑F – сумма внешних сил.
Известно, что импульс системы тел в общем случае зависит от времени и, соответственно, равен
где: m(t) – масса системы тел; v(t) – скорость системы тел.
Так как скорость — это производная по времени координат системы, то
где r – радиус-вектор.
В дальнейшем будем подразумевать зависимость от времени: массы, скорости и радиуса-вектора. Подставим (1.9) и (1.8) в (1.7) получим
Внесём массу m под знак дифференциала [ 1,с.295 ] , тогда
Производная разности равна разности производных
Проведём подробное дифференцирование каждого слагаемого по правилам дифференцирования произведений
+ r(d 2 m/dt 2 ) – r(d 2 m/dt 2 ) — (dm/dt)(dr/dt) = ∑F. (1.11)
Приведём подобные члены и запишем уравнение (1.11) в следующем виде
В правой части уравнения (1.12) сумма всех внешних сил. Последнее слагаемое называется силой переменной массы, то есть
Таким образом, к внешним силам добавляется ещё одна внешняя сила — сила переменной массы. Выражение в первой скобке правой части уравнения (1.13) — это скорость изменения массы, а выражение во второй скобке — это скорость отделения (присоединения) частиц. Таким образом, эта сила действует при изменении массы (реактивная сила) [ 2, с.120 ] системы тел с отделением (присоединением) частиц с соответствующей скоростью относительно этой системы тел. Уравнение (1.12) — это уравнение Мещерского [ 2, с.120 ] , знак минус указывает на то, что уравнение выведено в предположении действия внутренних сил (отделение частиц). Так как уравнение (1.12) выведено в предположении изменения импульса системы тел под воздействием внутренних сил, порождающих внешние, точным математическим методом, поэтому при его выводе в выражении (1.11) появились ещё две силы [17, с.102], которые не участвуют в изменении импульса системы тел, так как они при приведении подобных членов сокращаются. Перепишем уравнение (1.11), учитывая уравнение (1.13), не сокращая подобные члены, следующим образом
Обозначим предпоследний член выражения (1.14) через Fm, а последний через Fд , тогда
Так как сила Fm не участвует в изменении импульса, то её можно записать отдельным уравнением
Рассмотрим физический смысл уравнения (1.16), для этого перепишем его в следующем виде
Отношение силы к ускоренному росту массы в определённом объёме является величиной постоянной или пространство, занимаемое определённым количеством вида вещества, характеризуется минимальным объёмом. Сила Fm статическая и выполняет функцию давления.
Сила Fд также не участвует в изменении импульса системы тел, поэтому запишем её отдельным уравнением и рассмотрим её физический смысл
Сила Fд — это сила давления, оказываемая веществом, находящимся в жидком или газообразном состоянии на окружающее пространство. Характеризуется количеством, массой и скоростью частиц, обеспечивающих давление в определённом направлении. Следует отметить, что сила давления Fд совпадает с силой переменной массы Fпм и их разграничение произведено только для определения характера действия в различных условиях. Таким образом, уравнение (1.15) полностью описывает состояние вещества. То есть, рассматривая уравнение (1.15), можно заключить, что вещество характеризуется массой как мерой инертности, минимальным пространством, которое может занимать данное количество вещества без изменения его свойств и давлением, оказываемым веществом в жидком и газообразном состоянии на окружающее пространство.
§2. Характеристика действия сил инерции и переменной массы.
Поступательное ускоренное движение тела происходит под действием силы по второму закону Ньютона. То есть изменение величины скорости тела происходит при наличии ускорения и силы, вызвавшей это ускорение.
Использование центробежной силы инерции для поступательного движения возможно только при увеличении линейной скорости источников этих сил [18, с.88-90], так как при ускоренном движении системы силы инерции источников в направлении увеличения скорости системы уменьшаются вплоть до полного исчезновения. Кроме того, поле сил инерции должно быть неоднородным [4, с.101] и иметь максимальное значение в части системы по направлению поступательного движения.
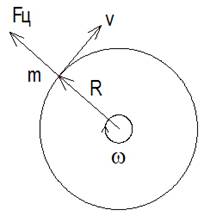
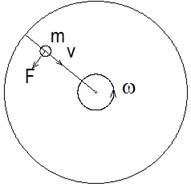
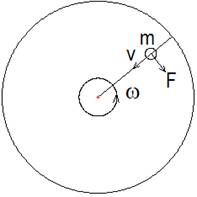
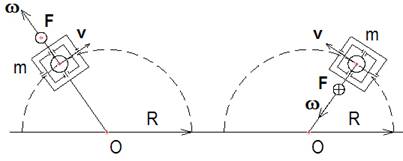
Рассмотрим движение тела (рис.2.1) массой m по окружности радиусом R.
Центробежная сила Fц , с которой тело давит на окружность, определяется [2, 365] формулой
Используя известное соотношение ω = v /R, где v линейная скорость тела перпендикулярная радиусу R, запишем формулу (2.1) в следующем виде
Центробежная сила действует в направлении радиуса R. Теперь мгновенно разорвём окружность, по которой движется тело. Опыт показывает, что тело полетит по касательной в направлении линейной скорости v, а не в направлении действия центробежной силы. То есть при отсутствии опоры, центробежная сила мгновенно исчезает.
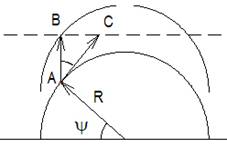
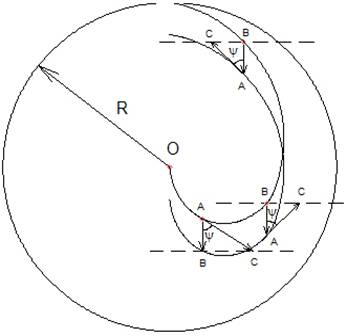
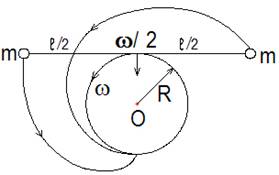
Пусть тело массой m движется по элементу полуокружности (рис.2.2) радиусом R, причём полуокружность движется с ускорением w П перпендикулярно диаметру.
При равномерном движении тела (линейная скорость не меняется по величине), и ускоренном полуокружности, опора в виде полуокружности мгновенно исчезает и центробежная сила будет равна нулю. Если тело движется с положительным линейным ускорением, то оно будет догонять полуокружность и, центробежная сила будет действовать. Найдём линейное ускорение w тела, при котором центробежная сила действует, то есть давит на полуокружность. Для этого время, затраченное телом на путь по касательной до пересечения со штриховой линией параллельной диаметру и проведённой через точку В (рис.2.2), должно быть меньше или равно времени, которое затратит полуокружность в направлении перпендикулярном диаметру. Пусть начальные скорости тела и полуокружности равны нулю и затраченное время одинаково, тогда путь SАС , пройденный телом
а путь, пройденный полуокружностью SАВ будет
Разделим уравнение (2.3) на (2.4) получим
Тогда ускорение тела w с учётом очевидного соотношения SАС / SАВ = 1/ cosΨ
Таким образом, проекция ускорения тела в элементе окружности на данное направление (рис.2.2) должна быть всегда больше или равна ускорению системы н том же направлении для поддержания в действии центробежной силы. То есть центробежная сила выступает в качестве поступательной движущей силы только при наличии положительного ускорения, изменяющей величину линейной скорости тела в системе
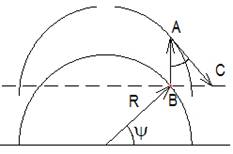
Аналогично получается соотношение для второй четверти полуокружности (рис.2.3).
Только путь, проходимый телом по касательной будет начинаться из точки на движущейся с ускорением полуокружности до пересечения со штриховой линией параллельной диаметру и, проходящей через точку А начального положения полуокружности. Угол в этом случае определяется интервалом π/2 ³ Ψ ³ 0.
Для системы, тело в которой движется равномерно или с замедлением по окружности, центробежная сила не вызовет поступательного ускоренного движения системы, так как линейное ускорение тела будет равно нулю или тело будет отставать от ускоренного движения системы.
Если тело вращается с угловой скоростью ω и одновременно приближается к центру окружности со скоростью v, тогда возникает [2, с.365] кориолисова сила
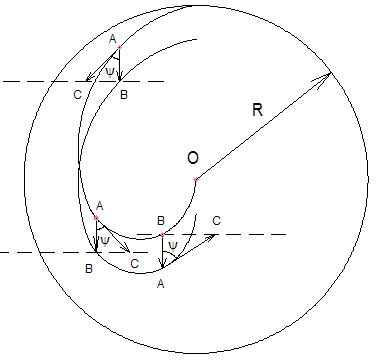
Типичный элемент траектория показана на рис.2.4.
Все формулы (2.3),(2.4),(2.5) и выводы для поддержания в действии центробежной силы циркулирующей среды будут верны и для кориолисовой силы, так как при ускоренном движении системы тело, движущееся с положительным линейным ускорением, будет успевать за ускорением системы и, соответственно, двигаться по криволинейной траектории, а не по касательной прямой, когда кориолисова сила отсутствует. Кривую надо разделить на две половины. В первой половине кривой (рис.4) угол меняется от начальной точки до нижней в интервале -π/2 £ Ψ £ π/2, а во второй половине от нижней точки до центра окружности π/2 ³ Ψ ³ 0. Аналогично, при вращении тела и одновременном удалении (рис.2.5) его от центра, кориолисова сила действует как поступательная при положительном ускорении величины линейной скорости тела.
Интервал углов в первой половине от центра окружности до нижней точки 0 £ Ψ £ π/2, а во второй половине от нижней точки до конечной π/2 ³ Ψ ³ -π/2.
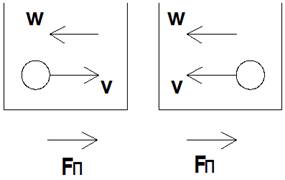
Рассмотрим поступательную силу [2,с.365] инерции Fп (рис.2.6), которая определяется по формуле
где w – ускорение тела.
При положительном ускорении тела она действует против движения, а при отрицательном ускорении (замедлении) она действует по направлению движения тела. При воздействии элемента ускорения или замедления (рис.2.6) на систему, с которой связаны элементы, ускорение тела элемента по модулю, очевидно, должно быть больше модуля ускорения системы, вызванной поступательной силой инерции тела. То есть поступательная сила инерции выступает в качестве движущей при наличии положительного или отрицательного ускорения.
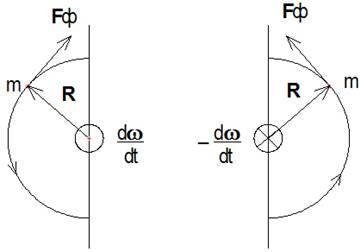
Фазовая сила инерции Fф (сила инерции, вызванная неравномерностью вращения) [2, с.365] определяется формулой
Пусть радиус R перпендикулярен вектору угловой скорости ω, тогда в скалярном виде формула (2.8) приобретает вид
При положительном угловом ускорении тела (рис.1.7) она действует против движения, а при отрицательном угловом ускорении (замедлении) она действует по направлению движения тела.
Используя известное соотношение ω = v /R, где v линейная скорость тела перпендикулярная радиусу R, запишем формулу (2.9) в следующем виде
Так как dv/dt = w , где w – линейное ускорение тела, то уравнение (2.10) приобретает вид
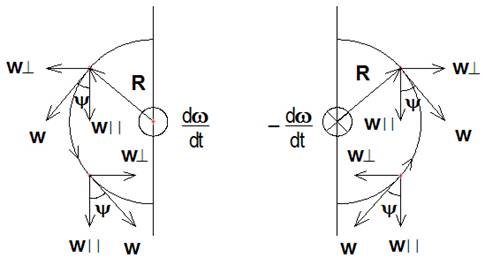
Таким образом, формула (2.11) аналогична формуле (2.7) для поступательной силы инерции, только ускорение w надо разложить на параллельную α II и перпендикулярную α ┴ составляющие (рис.2.8) по отношению к диаметру элемента полуокружности.
Очевидно, перпендикулярная составляющая ускорения w ┴ создаёт вращающий момент, так как в верхней части полуокружности она направлена влево, а в нижней части вправо. Параллельная составляющая ускорения w II создаёт поступательную силу инерции FфII, так как она направлена в верхней и нижней части полуокружности в одну сторону, совпадающую с направлением w II.
Используя соотношение w II = w cosΨ, получим
где угол Ψ находится в интервале -π/2 £ Ψ £ π/2.
Таким образом, получена формула (2.13) расчёта элемента фазовой силы инерции для поступательного движения. То есть фазовая сила инерции выступает в качестве движущей при наличии положительного или отрицательного линейного ускорения.
Итак, выделено четыре элемента поступательной силы инерции: центробежный, кориолисовый, поступательный, фазовый. Соединяя отдельные элементы определённым образом, можно соэдавать системы поступательной движущей силы инерции [3, с.198].
Рассмотрим силу переменной массы, определяемой формулой
Так как скорость отсоединения (присоединения) частиц относительно системы тел равна
тогда уравнение (2.14) запишем так
В уравнении (2.16) сила переменной массы ─ это значение силы, производимое отделяющейся частицей во время изменения её скорости от нуля до u или значение, производимое присоединяющейся частицей во время изменения её скорости от u до нуля. Таким образом, сила переменной массы действует в момент ускорения или замедления частиц, то есть она является поступательной силой инерции, но рассчитываемой по другим параметрам. С учётом выше написанного возникает необходимость уточнения вывода формулы Циолковского [2, с.116]. Уравнение (1.12) перепишем в скалярном виде и положим ∑F = 0, тогда
m(d 2 r/dt 2 ) = — (dm/dt)(dr/dt). (2.17)
Так как ускорение системы
d 2 r/dt 2 = dv/dt,
где v – скорость системы, тогда уравнение (2.17) с учётом уравнения (2.15) будет
m(dv/dt) = — (dm/dt)u. (2.18)
Умножим уравнение (2.17) на dt получим
то есть, зная максимальную скорость u = uO отделения частиц, которую считаем постоянной, можно по соотношению начальной mO и конечной масс m определить конечную скорость системы v
Уравнение (2.21) — это уравнение Циолковского.
§3. Контур циркулирующей среды центробежной силы инерции.
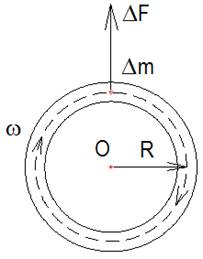
Рассмотрим циркуляцию среды по тору (рис. 3.1) со средним радиусом R, двигающейся с угловой скоростью ω относительно центра О. Модуль центробежной силы, действующий на точечный элемент потока массой ∆m, будет равен
В любом сечении кольца для одинаковых элементов центробежная сила будет по величине одинакова и направлена по радиусу от центра, растягивая кольцо. От направления вращения центробежная сила не зависит.
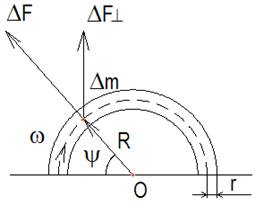
Теперь произведём расчёт суммарной центробежной силы [19, с.76-82], действующей перпендикулярно диаметру верхней полуокружности (рис.3.2). Очевидно, что в направлении из середины диаметра перпендикулярная проекция силы будет максимальна, плавно спадая к краям полуокружности, из-за симметричности кривой относительно средней линии. Кроме того, равнодействующая проекций центробежных сил, действующих параллельно диаметру, будет равна нулю, так как они равны и противоположно направлены.
Запишем элементарную функцию центробежной силы, действующей на точечный отрезок массой ∆m и длиной ∆ℓ:
Масса точечного элемента равна плотности потока, умноженной на его объём
Длина половины тора по средней линии
где π – число пи.
Объём половины тора
V = π 2 Rr 2 = πR π r 2 = ℓ π r 2 ,
где r – радиус трубки тора.
Для элементарного объёма запишем
Известно, что для окружности
Подставим выражение (3.3) в (3.2) получим:
Теперь подставим (3.4) в (3.1), тогда
∆F = ρ π r 2 ω 2 R 2 ∆Ψ.
Центробежная сила, действующая в перпендикулярном направлении (рис.2)
Известно, что cos((π/2)- Ψ) = sin Ψ, тогда
Подставим значение для ∆F получим
Найдём суммарную центробежную силу, действующую в перпендикулярном направлении в интервале от 0 до Ψ
F┴ = ∫ ρ π r 2 ω 2 R 2 sin ΨdΨ.
Проинтегрируем это выражение, тогда получим
F┴ = — ρ π r 2 ω 2 R 2 cosΨ│. (3.5)
Положим, что ускорение w циркулирующей среды в десять раз больше ускорения системы wс, то есть
В этом случае, согласно формуле (2.5) получим
Вычислим угол действия сил инерции в радианах
что соответствует углу в 84 градуса.
Таким образом, угловой интервал действия сил инерции составляет
0 £ Ψ £ 84° в левой половине контура и симметрично 96° £ Ψ £ 180° в правой половине контура. То есть интервал отсутствия действующих сил инерции во всём контуре составляет около 6,7% (реально, ускорение циркулирующей среды значительно больше ускорения системы, поэтому интервал отсутствия действующих сил инерции будет менее 1% и его можно не учитывать). Для определения суммарной центробежной силы, в этих интервалах углов, достаточно подставить первый интервал в формулу (3.5) и, вследствие симметрии, умножить на 2 получим
F┴ = — 2ρ π r 2 ω 2 R 2 cosΨ│. (3.6)
После несложных вычислений получаем
F┴ = 1,8 ρ π r 2 ω 2 R 2 .
Известно, что угловая скорость
F┴ = 1,8 ρ π r 2 v 2 .
Так как циркулирующая среда должна двигаться с ускорением, чтобы действовала сила инерции, поэтому выразим линейную скорость через ускорение, полагая начальную скорость равной нулю
F┴ = 1,8 ρ π r 2 (w t) 2 . (3.8)
Среднее значение [1, с.451] за время действия положительного ускорения, которое считаем постоянным, будет
F┴СР = ((1,8ρ π r 2 w 2 )/t) ∫t 2 dt.
После вычислений получаем
F┴СР = 0,6ρ π r 2 w 2 t 2 . (3.9).
Таким образом, был выделен контур циркулирующей среды, из которых можно составить замкнутую цепь и просуммировать их центробежные силы.
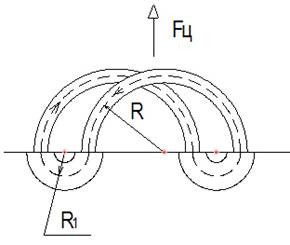
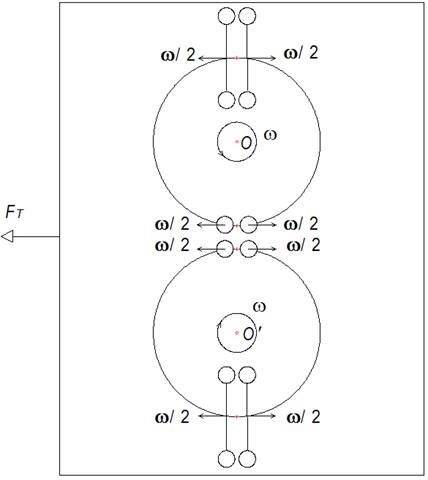
Составим замкнутую цепь из четырёх контуров разных сечений (рис.3.3): два верхних контура радиусом R. сечением S и два нижних контура радиусом R1 сечением S1, пренебрегая краевыми эффектами при переходе циркулирующей среды с одного сечения на другое. Пусть S 2 /r 2 , (3.10)
где r1 и r радиусы потока циркулирующей среды соответствующего сечения.
Кроме того, запишем очевидное отношение для скоростей и ускорений
Найдём ускорение среды нижнего контура, используя для вычислений уравнение (3.10) и (3.11)
Теперь, согласно уравнению (3.9), определим центробежную силу для нижнего контура, учитывая уравнение (3.12) и после вычислений получим
F┴СР1 = 0,6 ρ π r1 2 w1 2 = 0,6ρ π r 2 w 2 t 2 (r 2 / r1 2 ) = F┴СР (r 2 / r1 2 ) (3.13)
При сравнении выражения для центробежной силы верхнего контура (3.9) и нижнего контура (3.13) вытекает, что они отличаются на величину (r 2 / r1 2 ).
Равнодействующая центробежных сил, действующая на два контура в верхней полуплоскости (граница верхней и нижней полуплоскости показана тонкой линией) противоположно направлена равнодействующей центробежных сил, действующей на два контура в нижней полуплоскости. Очевидно, что суммарная FЦ центробежная сила будет действовать в направлении, как показано на рисунке 3.3, примем это направление за положительное. Вычислим суммарную FЦ центробежную силу
FЦ = 2 F┴СР — 2F┴СР1 = 1,2ρ π r 2 w 2 t 2 (1- (r 2 / r1 2 )) (3.14)
Как видим, суммарная центробежная сила зависит от плотности потока, сечений противоположных контуров и ускорения потока. От радиуса контуров суммарная центробежная сила не зависит. Для системы, циркулирующая среда в которой движется равномерно или с замедлением по окружности, центробежная сила не вызовет поступательного ускоренного движения системы.
Таким образом, был выделен базисный контур циркулирующей среды, показана возможность использования контуров циркулирующей среды разных сечений для суммирования центробежной силы в определённом направлении и изменения общего импульса замкнутой системы тел под действием внешних сил инерции, вызванных внутренними силами.
Пусть r = 0,025м; r1 = 0,05м; ρ = 1000 кг/м 3 ; w = 5м/с 2 , t = 1с, тогда за время действия положительного ускорения среднее значение суммарной центробежной силы FЦ. ≈ 44Н.
§4. Контур циркулирующей среды кориолисовой силы инерции.
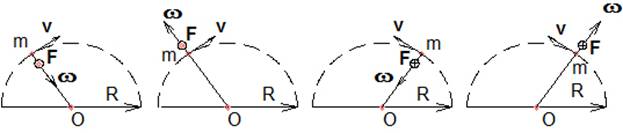
Известно, что кориолисова сила инерции возникает при вращении тела массой m по окружности и одновременном радиальном перемещении его, причём она перпендикулярна угловой скорости ω и скорости радиального перемещения v. Направление кориолисовой силы F совпадает с направлением векторного произведения в формуле F = 2m[v w ].
На рис.4.1 показано направление кориолисовой силы при вращении тела по окружности против часовой стрелки и радиальном перемещении его к центру окружности за первый полупериод,. а на рис.4.2 показано направление кориолисовой силы при вращении тела по окружности также против часовой стрелке и радиальном перемещение его от центра окружности за второй полупериод.
Совместим левую часть движения тела на рис.4.1 и правую часть на рис.4.2. тогда получим на рис. 4.3 вариант траектории движения тела за период.
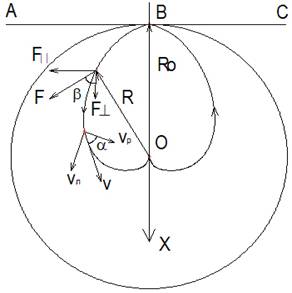
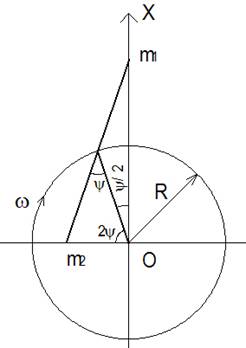
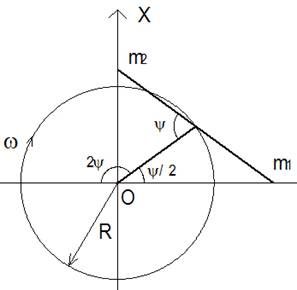
Рассмотрим движение циркулирующей среды (жидкости) по трубам изогнутым соответственно траектории. Кориолисовы силы левой и правой кривой действуют в секторе 180 градусов в радиальном направлении при движении от точки В к точке О влево и вправо соответственно относительно оси Х. Составляющие кориолисовой силы левой и правой кривой F | | параллельные прямой АС компенсируют друг друга, так как одинаковы, противоположно направлены и симметричны относительно оси Х. Симметричные составляющие кориолисовой силы левой и правой кривой F ^ перпендикулярные прямой АС складываются, так как направлены в одну сторону.
Вычислим величину кориолисовой силы, действующей по оси Х на левой половине траектории. Так как составление уравнения траектории представляет сложную задачу, то решение по нахождению кориолисовой силы ищем приближённым методом. Пусть v — это скорость жидкости постоянная по всей траектории. Радиальную скорость vр и линейную скорость вращения vл , согласно теореме параллелограмма скоростей, выразим (рис.3) через скорость v и угол α
Траектория движения (рис.4.3) построена с учётом того, что в точке В радиальная скорость vр равна нулю, а линейная vл равна v. В центре окружности О, радиусом Rо, радиальная скорость vр равна v, а линейная vл равна нулю, причём касательная траектории в центре окружности перпендикулярна касательной траектории в начале (точка В). Радиус монотонно уменьшается от Rо до нуля. Угол α меняется от 90° в точке В до 0° в центре окружности. Тогда, из графических построений, выбираем длину траектории 1/4 длины окружности радиусом R0. Теперь можно вычислить массу жидкости, используя формулу объёма тора. То есть масса циркулирующей среды будет равна 1/4 массы тора со средним радиусом R0 и внутренним радиусом трубы r
m = ρπ 2 r 2 R0 /2, (4.1)
где ρ – плотность жидкости.
Модуль проекции кориолисовой силы в каждой точке траектории на ось Х находим по формуле
F ^ = 2m vр ср ωср cos b , (4.2)
где vр ср – среднее значение радиальной скорости; ωср – среднее значение угловой скорости; b – угол между кориолисовой силой F и осью Х (-90 ° £ b £ 90 ° ).
Для технических расчётов можно не учитывать интервал отсутствия действия сил инерции, так как ускорение циркулирующей среды значительно больше ускорения системы. То есть выбираем интервал углов между кориолисовой силой F и осью Х (-90 ° £ b £ 90 ° ). Угол α меняется от 90° в точке В до 0° в центре окружности, тогда среднее значение радиальной скорости
vр ср = 1 / (0 — π/2) ∫ v cos α dα = 2 v / π. (4.3)
Среднее значение угловой скорости будет равно
ωср = (1/ ((v π /2Rо) — v Rо))) ∫ ω dω = (v /2Rо) ((π /2.) +1). (4.4)
Нижний предел угловой скорости интеграла в формуле (4.4) определяем в начальной точке В. Он, очевидно, равен v /Rо. Верхнее значение интеграла определяем как предел отношения
ℓim (vл /R) = ℓim (v sinα /R), (4.5)
где R – текущий радиус.
Воспользуемся известным методом [ 7, с.410 ] отыскания пределов для функций нескольких переменных: функция vsinα /R в точке (R= 0, α = 0) на любой прямой R = kα , проходящей через начало координат имеет предел. В данном случае предел не существует, но существует предел для определённой прямой. Найдём коэффициент к в уравнении прямой, проходящей через начало координат.
При α = 0 ® R= 0, при α = π /2 ® R= Rо (рис.3), отсюда к = 2Rо/π , тогда формула (5) преобразуется к виду, включающем первый замечательный предел
ℓim (v π sinα /2Rо α) = (v π/2Rо) ℓim sinα/α = v π/2Rо. (4.6)
Теперь подставим полученное значение из формул (4.1), (4.3) и (4.4) в (4.2) получим
F ^ = ρ π r 2 v 2 ((π /2.) +1) cos b .
Найдём сумму проекций кориолисовой силы в интервале (-90 ° £ b £ 90 ° ) для левой кривой.
F ^ = ρ π r 2 v 2 ((π /2.) +1) ∫ cos b d b = 2 ρ π r 2 v 2 ((π /2.) +1).
Окончательно сумма проекций кориолисовой силы для левой и правой кривой
∑F ^ = 4ρ r 2 v 2 ((π /2.) +1). (4.7)
Согласно соотношению (3.7), уравнение (4.7) перепишем в виде
∑F ^ = 4ρ r 2 (w t) 2 ((π /2.) +1). (4.8)
Вычислим среднее значение кориолисовой силы по времени, считая ускорение постоянным
Fк = ∑F ^ ср = 4ρ r 2 w 2 ((π /2.) +1) / t) ∫t 2 dt.
После вычислений получаем
Fк ≈ 1,3ρ r 2 w 2 ((π /2.) +1)t 2 . (4.9)
Пусть r = 0,02м; w = 5м/с 2 ; ρ = 1000кг/м 3 ; t = 1c, тогда суммарная средняя кориолисова сила инерции за время действия положительного ускорения циркулирующей среды будет Fк ≈ 33Н.
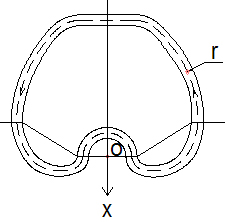
В центре окружности в траектории имеется перегиб (рис.4.3), который можно интерпретировать, для упрощения расчётов, как полуокружность с малым радиусом. Для наглядности разделим траекторию на две половины и вставим в нижнюю часть полуокружность, а в верхнюю часть прямую, как показано на рис.4.4 и направим циркулирующую среду по трубе радиусом r, изогнутой по форме траектории.
В формуле (3.5) положим угол Ψ = 180 ° , тогда суммарная центробежная сила Fц, действующая в перпендикулярном направлении для контура циркулирующей среды
Fц = 2 ρπ r 2 v 2 . (4.10)
Таким образом, центробежная сила не зависит от радиуса R, а зависит только от угла интегрирования (см. формулу (3.5)) при постоянной плотности потока ρ, радиуса r и скорости циркулирующей среды v в каждой точке траектории. Так как радиус R может быть любым, то можно заключить, что для любой выпуклой кривой с краями перпендикулярными прямой АОБ (рис.3.2) центробежная сила будет определяться выражением (4.10). Следует отметить, как следствие, что каждый край выпуклой кривой может быть перпендикулярен своей прямой, которые параллельны и не лежат на одной линии.
Сумма проекций центробежных сил (рис.4), действующих против направления оси Х, возникающих в полуокружности и двух половинках выпуклой кривой (прямая не вносит вклад в центробежную силу) над ломаной линией и проекций, действующих по оси Х, возникающих в двух выпуклых кривых под ломаной линией компенсируются, так как они одинаковы и направлены в противоположные стороны. Таким образом. центробежная сила не вносит вклад в поступательное движение.
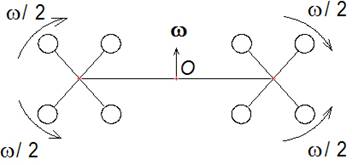
§5. Твёрдотельные вращательные системы. Центробежные силы инерции.
1. Вектор собственной угловой скорости стержней перпендикулярен вектору угловой скорости центра масс стержня и радиусу общей оси вращения стержней.
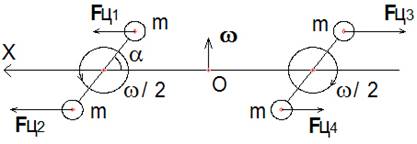
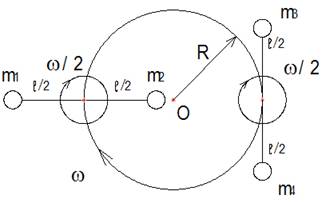
Энергия поступательного движения может переходить в энергию вращательного движения и наоборот [6, с.427]. Рассмотрим пару противоположных стержней длиной ℓ с точечными грузами одинаковой массы на концах, равномерно вращающихся вокруг собственного центра масс и вокруг общего центра О радиусом R с угловой скоростью ω (рис. 5.1): полуоборот стержня за один оборот вокруг общей оси. Пусть R ³ ℓ/2. Для полного описания процесса достаточно рассмотреть вращение в интервале углов 0 £ α £ π/2. Расставим силы, действующие параллельно оси Х, проходящей через общий центр О и положение стержней под углом α = 45 градусов, в плоскости оси Х и общей оси вращения, как показано на рисунке 5.1.
Угол α связан с частотой ω и временем t соотношением
так как полуоборот стержня происходит за один оборот вокруг общей оси. Очевидно, что центробежные силы инерции удалённых грузов от центра будут больше, чем ближних. Проекции центробежных сил инерции на ось Х будут
Fц1 = mω 2 (R — (ℓ/2) cos α) sin 2 α (5.1.2)
Fц2 = mω 2 (R + (ℓ/2) cos α) sin 2 α (5.1.3)
Fц3 = — mω 2 (R + (ℓ/2) sin α) sin 2 α (5.1.4)
Fц4 = — mω 2 (R — (ℓ/2) sin α) sin 2 α (5.1.5)
Запишем разностную центробежную силу инерции , действующую на удалённые грузы. Разностная центробежная сила инерции на второй груз
Fц2-1 = mω 2 ℓ cos α sin2 α. (5.1.6)
Разностная центробежная сила инерции на третий груз
Fц3-4 = — mω 2 ℓ sin α sin2 α. (5.1.7)
Среднее значение разностных центробежных сил инерции за полуоборот будет
Fср ц2-1 = (1/(π/2))∫ mω 2 ℓ cos α sin2 αdα = 4mω 2 ℓ/3 π » 0,4mω 2 ℓ, (5.1.8)
Fср ц3-4 = (1/(π/2))∫ mω 2 ℓ sin α sin2 αdα = -4mω 2 ℓ/3 π » — 0,4mω 2 ℓ. (5.1.9)
Получили две противоположные и равные по модулю центробежные силы инерции, которые являются внешними. Поэтому их можно представить в виде двух одинаковых бесконечно удалённых тел (не входящих в систему), одновременно взаимодействующих с системой: к первому телу второй груз подтягивает систему, а от второго тела третий груз отталкивает систему.
Среднее значение силы принудительного воздействия на систему за полуоборот по оси Х равно сумме сил подтягивания Fср ц2-1 и отталкивания Fср ц3-4 от внешних тел
Fп = | Fср ц2-1 | + | Fср ц3-4 | = 0,8 m ω 2 ℓ. (5.1.10)
Для устранения вращающего момента системы из двух стержней в вертикальной плоскости (рис.5.2) необходимо применить ещё пару противоположных стержней, вращающихся синхронно в одной плоскости в противоположную сторону.
Для устранения вращающего момента системы по общей оси с центром О применяем такую же пару из четырёх стержней, но вращающихся в противоположную сторону относительно общей оси (рис.5.3).
Окончательно, для системы из четырёх пар вращающихся стержней (рис.5.3) сила тяги будет
Fт = 4Fп = 3,2mω 2 ℓ . (5.1.11)
Пусть m = 0,1кг; ω =2 πf, где f = 10об/с; ℓ = 0,5м, тогда Fт ≈ 632Н.
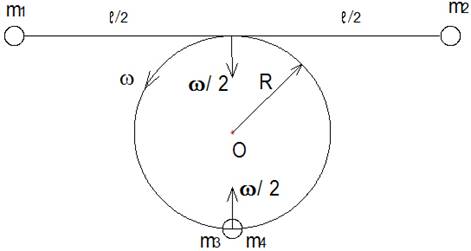
2. Вектор собственной угловой скорости стержней перпендикулярен вектору угловой скорости центра масс стержня и параллелен радиусу общей оси вращения стержней.
Рассмотрим пару противоположных перпендикулярных друг другу стержней длиной ℓ с точечными грузами одинаковой массы на концах, равномерно вращающихся вокруг собственного центра масс и вокруг общего центра О радиусом R с угловой скоростью ω (рис. 5.4): полуоборот стержня за один оборот вокруг общей оси.
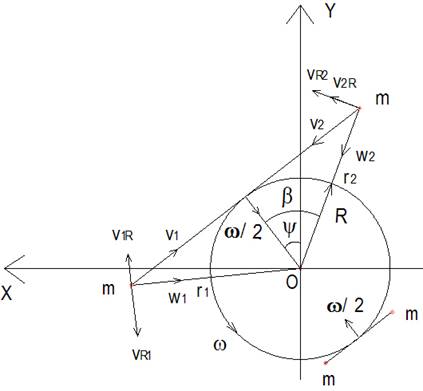
Для вычисления выбираем только m1 и m2, так как для m3 и m4 решение аналогичное. Определим угловые скорости грузов относительно общего центра О. Модули проекций линейной скорости грузов относительно собственного центра масс параллельно плоскости вращения относительно общего центра О будут (рис.5.5)
v1 = v2 = (ωℓ/4) sin ( Ψ /2), (5.2.1)
Выделим по модулю проекции касательной этих скоростей перпендикулярных радиусам r1 и r2 соответственно относительно центра О получим
v1R = v2R = ( ω ℓ/4) sin ( Ψ /2) cos b , (5.2.2)
cos b = R /r1 = R /r2 =R/ Ö (R 2 +(ℓ 2 /4) cos 2 ( Ψ /2)), (5.2.3)
R – расстояние от центра О до центра масс грузов, r1, r2 – расстояние от грузов до центра О, причём r1 = r2.
Модули линейной скорости грузов относительно общего центра О без учёта их линейной скорости относительно собственного центра масс будут
Найдём суммарную угловую скорость каждого груза относительно общей оси вращения, учитывая, что линейные скорости противоположно направлены у первого груза и одинаково у второго, тогда
ω1 = (vR1 — v1R)/r1 = ω [ 1– (ℓR sin ( Ψ /2))/4(R 2 +(ℓ 2 /4)cos 2 ( Ψ /2)) ] , (5.2.6)
ω2 = (vR2 + v2R)/r2 = ω [ 1+ (ℓR sin ( Ψ /2))/4(R 2 +(ℓ 2 /4)cos 2 ( Ψ /2)) ] . (5.2.7)
Соответственно центробежные силы составят
F1 = mω 2 [ (1– (ℓR sin ( Ψ /2))/4(R 2 +(ℓ 2 /4)cos 2 ( Ψ /2)) ] 2 Ö (R 2 +(ℓ 2 /4)cos 2 ( Ψ /2)), (5.2.8)
F2 = mω 2 [ (1+ (ℓR sin ( Ψ /2))/4(R 2 +(ℓ 2 /4)cos 2 ( Ψ /2)) ] 2 Ö (R 2 +(ℓ 2 /4)cos 2 ( Ψ /2)). (5.2.9)
Рассмотрим вариант, когда ℓ= 4R. В этом случае, при Ψ=180 ° угловая частота первого груза ω1 = 0 и она не меняет направление, у второго груза ω2 = 2ω (рис.5.6).
Перейдём к определению центробежных сил в направлении оси Х при ℓ= 4R
F1 = mω 2 R [ (1+ 4cos 2 ( Ψ /2)– sin ( Ψ /2))/(1+4cos 2 ( Ψ /2)) ] 2 Ö (1 + 4cos 2 ( Ψ /2)), (5.2.10)
F2 = mω 2 R [ (1+ 4cos 2 ( Ψ /2)+ sin ( Ψ /2))/(1+4cos 2 ( Ψ /2)) ] 2 Ö (1 + 4cos 2 ( Ψ /2)). (5.2.11)
Следует отметить, что с ростом угла Ψ от 0 до 180 ° в точке Ψ = b = 60 ° проекция центробежной силы F2 меняет знак с отрицательного на положительный.
Сначала, сложим средние значения проекции на ось Х центробежной силы первого груза и среднее значение проекции второго в интервале угла
0 £ Ψ £ 60 ° , учитывая знаки, так как они противоположно направлены
FСР 1-2 = (1/(π /3))∫ (F1 sin( b + Ψ) — F2 sin( b — Ψ))dΨ ≈ 0,6mω 2 R, (5.2.12)
где b = arccos (1 / Ö (1 +4 cos 2 ( Ψ /2))) определяется из формулы (5.2.3).
Центробежная сила FСР 1-2 в формуле (5.2.12) положительна, то есть направлена по оси Х. Теперь сложим одинаково направленные среднее значение проекции на ось Х центробежной силы первого груза и среднее значение проекции второго в интервале угла 60 ° £ Ψ £ 180 °
FСР 1+2 = (1/(π-(π/3)))∫(F1 sin(Ψ + b )+ F2 sin(Ψ — b ))dΨ ≈ 1,8mω 2 R, (5.2.13)
Среднее значение в интервале 0 ° £ Ψ £ 180 ° , очевидно, будет
Для m3 и m4 среднее значение проекции на ось Х центробежной силы будет таким же, но действующей в противоположную сторону.
Для устранения вращающего момента необходимо применить ещё одну пару стержней, но вращающихся в противоположную сторону относительно собственного центра масс и относительно общей оси вращения, тогда окончательно сила тяги будет
Пусть m = 0,1кг; ω =2 πf, где f = 10об/с; ℓ= 4R , где R = 0,1м, тогда FТ ≈ 220Н.
3. Вектор собственной угловой скорости стержней параллелен и одинаково направлен с вектором угловой скорости центра масс стержня, вращающегося относительно общей оси.
Рассмотрим пару противоположных , лежащих водной плоскости, стержней длиной ℓ с точечными грузами одинаковой массы на концах, равномерно вращающихся вокруг собственного центра масс и вокруг общего центра О радиусом R с угловой скоростью ω (рис. 5.7): полуоборот стержня за один оборот вокруг общей оси.
Аналогично предыдущему случаю для вычисления выбираем только m1 и m2, так как для m3 и m4 решение аналогичное. Приблизительную оценку действующих сил инерции произведём при ℓ = 2R с использованием средних значений угловой скорости относительно центра О, а также средних значений расстояния от грузов до центра О. Очевидно, угловая скорость первого груза в начале будет 1,5ω второго груза 0,5ω , а через полуоборот у обоих ω. Расстояние от первого груза до центра О в начале 2R от второго груза 0, а через полуоборот от каждого R Ö 2.
Причём в интервале 0 ° £ Ψ £ 36 ° (рис. 5.8) центробежные силы складываются в направлении оси Х, в интервале 36 ° £ Ψ £ 72 ° (рис. 5.8, рис. 5.9) из силы первого тела вычитается сила второго и их разность действует по оси Х, в интервале 72 ° £ Ψ £ 90 ° (рис. 5.9) силы складываются и действуют противоположно оси Х.
Определим средние значения угловой скорости и радиусов грузов за полуоборот.
Средняя угловая скорость первого груза
ω СР 1 = ( ω + 0,5ω + ω)/2 = 1,25ω. (5.3.1)
Средняя угловая скорость второго груза
ω СР 2 = ( ω — 0,5ω + ω)/2 = 0,75ω. (5.3.2)
Средний радиус первого груза
R СР 1 = (2R + R Ö 2)/2 = R (2 + Ö 2)/2. (5.3.3)
Средний радиус второго груза
R СР 2 = (0 + R Ö 2)/2 = (R Ö 2)/2. (5.3.4)
Проекция центробежной силы, действующей на первый груз в направлении оси Х, будет
F 1 = m ω 2 СР 1 R СР 1 cos(Ψ /2)sin2Ψ » 2 ,67mω 2 R cos(Ψ /2)sin2Ψ . (5.3.5)
Проекция центробежной силы, действующей на второй груз в направлении оси Х, будет
F 2 = m ω 2 СР 2 R СР 2 sin(Ψ /2)sin2Ψ » 0 ,4mω 2 R sin(Ψ /2)sin2Ψ . (5.3.6)
Среднее значение суммы проекций центробежных сил первого и второго грузов в интервале 0 ° £ Ψ £ 36 ° составит
F СР 1 + 2 = (1 /0,2 π) ∫ (F 1 + F 2 )dΨ » 1 ,47mω 2 R. (5.3.7)
Среднее значение разности проекций центробежных сил первого и второго грузов в интервале 36 ° £ Ψ £ 72 ° составит
F СР 1 — 2 = (1 /0,2 π) ∫(F 1 — F 2 ) dΨ » 1 ,95mω 2 R. (5.3.8)
Среднее значение суммы проекций центробежных сил первого и второго грузов в интервале 72 ° £ Ψ £ 90 ° составит
F СР- (1 + 2) = — (1 /0,1 π) ∫(F 1 + F 2 )dΨ » -3 ,72mω 2 R. (5.3.9)
Среднее значение суммы проекций центробежных сил первого и второго грузов в интервале 0 ° £ Ψ £ 90 ° составит
F СР = (2F СР 1 + 2 + 2F СР 1 – 2 + F СР- (1 + 2) )/5 » 0,62 mω 2 R. (5.3.10)
Аналогично вычисляется сумма проекций центробежных сил для третьего и четвёртого грузов.
Для устранения вращающего момента необходимо применить ещё одну пару стержней, но вращающихся в противоположную сторону относительно собственного центра масс и относительно общей оси вращения, тогда окончательно сила тяги будет
FТ = 4F СР = 2,48m ω 2 R. (5 .3.11)
Пусть m = 0,1кг; ω =2 πf, где f = 10об/с; R = 0,25м, тогда FТ ≈ 245Н.
§6. Фазовая сила инерции.
Для реализации фазовой силы инерции в качестве поступательной используем двухкривошипный шарнирный четырёхзвенник, чтобы преобразовать равномерное вращение двигателя в неравномерное вращение грузов по определённому режиму с оптимизацией характера движения грузов для эффективного использования сил инерции, а соответствующим выбором взаимного расположения грузов, компенсировать обратный импульс
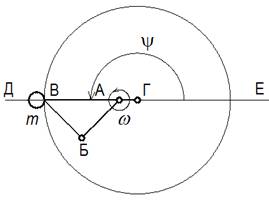
Шарнирный четырёхзвенник будет двухкривошипным, если межцентровое расстояние АГ (Рис.6.1) будет меньше длины любого подвижного звена, а сумма межцентрового расстояния и длины наибольшего из подвижных звеньев будет меньше суммы длин двух других звеньев.
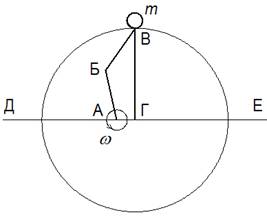
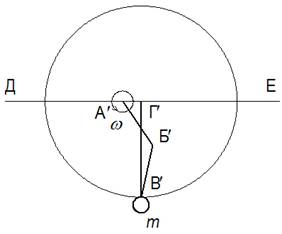
Звено ВГ (рычаг), на котором закреплён груз массой m, является ведомым кривошипом на неподвижном валу Г, а звено АБ ведущим. Звено А – это вал двигателя. Звено БВ является шатуном. Соотношение длин шатуна и ведущего кривошипа выбирается таким, чтобы при достижении грузом крайней точки Д был прямой угол между шатуном и ведущим кривошипом, что обеспечивает максимальный КПД. Тогда при равномерном вращении вала двигателя А с ведущим кривошипом АБ с угловой скоростью w шатун БВ передает движение ведомому кривошипу ВГ, замедляя его. Таким образом, груз замедляется от точки Е до точки Д по верхней полуокружности. В этом случае сила инерции действует по направлению движения груза. Рассмотрим движение груза в противоположной полуокружности (Рис. 6.2), где шатун, выпрямляясь, ускоряет груз.
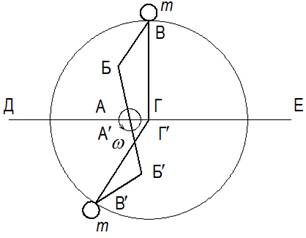
В этом случае сила инерции действует против направления движения груза, совпадая с направлением силы инерции в первой полуокружности. Объединённая схема движителя показана на рисунке 6.3.
Ведущие кривошипы АБ и А ¢ Б ¢ жёстко соединены по прямой на валу двигателя, а ведомые кривошипы (рычаги) независимо друг от друга вращаются на неподвижном валу. Продольные составляющие сил инерции в направлении от точки Е до точки Д верхнего груза и нижнего складываются, обеспечивая поступательное движение. Обратный импульс отсутствует, так как грузы вращаются в одном направлении и, в среднем, симметрично противоположно расположены.
Проведём оценку действующей фазовой силы инерции.
Пусть АБ = БВ = r, ГВ = R.
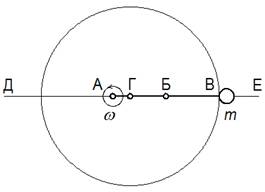
Предположим, что в крайнем правом положении угол Ψ между радиусом R и средней линией ДЕ равен 0 ° (Рис.6.4) и
r + r – АГ = R, (6 .1)
а также в крайнем левом положении при Ψ =180 ° (Рис.6.5) угол
Ð АБВ = 90 ° . (6 .2)
Тогда, исходя из этих условий, легко определить, что предположения выполняются при следующих значениях
АГ = (3 — 2 Ö 2)R. (6 .4)
Теперь определим угловые скорости в крайнем правом и левом положениях. Очевидно, в правом положении угловые скорости АГ и ГВ совпадают и равны w .
В левом положении угловая скорость w ГВ будет, очевидно, равна
w ГВ = (180 ° /225 ° ) w . (6 .5)
Приращение угловой скорости ∆ w за время ∆t = 225 ° / w = 5π/4 w составит
∆ w = w ГВ — w = — 0,2 w . (6 .6)
Пусть угловое ускорение будет равнозамедленное, тогда
dω/dt = ∆ w /∆t = — 0,16 w 2 / π. (6 .7)
Воспользуемся формулой фазовой силы инерции (2.8) в скалярном виде
Fф = -m [(dω/dt)R] = 0,16m w 2 R/ π. (6.8)
Проекция фазовой силы инерции в направлении ЕД будет
FфЕД = 0,16m w 2 RsinΨ/π. (6.9)
Среднее значение проекции фазовой силы инерции за полупериод
FСР = 0 ,16mω 2 R/ π 2 ) ∫ sinΨdΨ = 0 ,32mω 2 R/ π 2 . (6.10)
Для двух грузов (рис.6.3) сила удваивается. Для устранения вращающего момента необходимо применить ещё одну пару грузов, но вращающихся в противоположную сторону. Окончательно, сила тяги для четырёх грузов составит
FТ = 4FСР = 1 ,28mω 2 R/ π 2 . (6.11)
Пусть m = 0,1кг; ω =2 πf, где f = 10об/с; R = 0,5м, тогда FТ = 25,6Н.
§7. Гироскоп. Кориолисова и центробежная сила инерции.
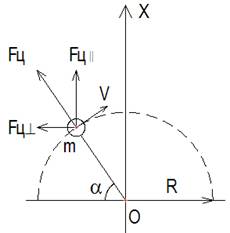
Рассмотрим колебательное движение груза [19, с.76-82] массой m по полуокружности (рис.7.1) радиусом R с линейной скоростью v. Центробежная сила инерции Fц, действующая на груз массой m будет равна m v 2 /R, направлена по радиусу от центра О. Проекция центробежной силы на ось Х будет равна
F ц ׀׀ = (m v 2 /R) sin α . (7.1)
Груз должен двигаться с ускорением w по окружности, чтобы центробежная сила была действующей для поступательного движения системы, а так как v = wt, тогда
F ц ׀׀ = (m w 2 t 2 /R) sin α , (7.2)
Из-за инертности груза на краях полуокружности появляется обратный импульс, который препятствует поступательному движению системы в направлении оси Х.
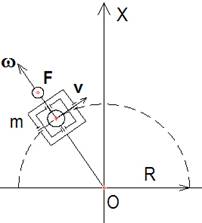
Известно, что при воздействии силы, изменяющей направление оси гироскопа, он прецессирует под воздействием кориолисовой силы, причём это движение безинерционно. То есть при мгновенном приложении силы, изменяющей направление оси вращения, гироскоп мгновенно начинает прецессировать и так же мгновенно останавливается при исчезновении этой силы [8, с.258-259]. Вместо груза применяем гироскоп, вращающийся с угловой скоростью ω. Теперь приложим силу F перпендикулярно к оси вращения гироскопа (рис.7.2) и будем воздействовать на ось так, чтобы держатель с гироскопом совершал безинерционное колебательное движение (прецессировал) в определённом секторе (в оптимальном случае с конечным значением α = 180°). Мгновенная остановка прецессии держателя с гироскопом и возобновление её в обратную сторону происходит, когда направление силы F меняется на противоположное. Таким образом, происходит колебательное безинерционное движение держателя с гироскопом, что исключает обратный импульс, препятствующий поступательному движению по оси Х.
Угловая скорость прецессии [8, с.257]
где: М – момент силы; IZ – момент инерции гироскопа; ω – угловая скорость гироскопа.
Момент силы (подразумевается, что ℓ перпендикулярно F)
где: ℓ – расстояние от точки приложения силы F до центра инерции гироскопа; F – сила, приложенная к оси гироскопа.
Подставим (7.4) в (7.3) получим
dα /dt = ℓ F / IZ ω, (7.5)
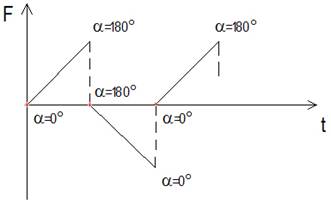
В правой части формулы (7.5) составляющие ℓ , IZ , ω считаем постоянными, а сила F, в зависимости от времени t, пусть меняется по кусочно-линейному закону (рис.7.3).
Известно, что линейная скорость связана с угловой скоростью следующим соотношением
Дифференцируя по времени формулу (7.6) получим ускорение
w = R (d 2 α /dt 2 ). (7.7)
Подставим формулу (7.5) в формулу (7.7) получим
w = (R ℓ / IZ ω ) (dF/dt) . (7.8)
Таким образом, ускорение зависит от скорости изменения силы F, что делает центробежную силу действующей для поступательного движения системы.
Следует отметить, что при большой угловой скорости ω и dα /dt ω , возникающий гироскопический момент уравновешивает момент силы F, поэтому движения в направлении воздействия этой силы не происходит [8, с.260].
Для компенсации перпендикулярной проекции центробежной силы Fц┴ применяем второй такой же гироскоп, совершающий колебательное движение синхронно в противофазе с первым гироскопом (рис.7.4). Проекция центробежной силы Fц┴ у второго гироскопа будет направлена встречно проекции у первого. Очевидно, что перпендикулярные составляющие Fц┴ скомпенсируются, а параллельные Fц ׀׀ сложатся.
Если сектор колебаний гироскопов будет не более полуокружности, то не будет возникать противоположная центробежная сила, уменьшающая центробежную силу в направлении оси Х.
Для устранения вращающего момента устройства, возникающего из-за принудительного вращения оси гироскопов, необходимо установить ещё одну пару таких же гироскопов, оси которых вращаются в противоположную сторону. Секторы колебательного движения держателей с гироскопами в паре, оси гироскопов которых вращаются в одну сторону, должны быть симметрично направлены в одну сторону с секторами держателей с гироскопами, оси гироскопов которых вращаются в другую сторону (рис.7.5).
Вычислим среднее значение [1, с.451] проекции Fц ׀׀ центробежной силы для одного гироскопа (рис.7.2) на держателе, колеблющегося в секторе полуокружности от 0 до π и обозначим это значение через Fп
Fп = (1/ π ) ∫ (m w 2 t 2 / R) sin α dα = 2m w 2 t 2 / Rπ. (7.9)
Для четырёх гироскопов на держателях среднее значение поступательной силы Fп за каждый полупериод будет:
Fп = 8m w 2 t 2 / Rπ. (7.10)
Пусть масса держателя намного меньше массы гироскопа, а масса гироскопа m = 1кг. Ускорение w = 5м/с 2 , причём ускорение гироскопа на порядок больше ускорения системы, тогда можно не учитывать небольшой интервал отсутствия действия центробежной силы в центре. Время нарастания скорости t = 1с. Радиус (длина) держателя R = 0,5м. Тогда по формуле (7.10) поступательная сила будет Fп = 8∙ 1∙ 5 2 ∙1 2 /0,5 π ≈ 127Н.
1. Выгодский М. Я. Справочник по высшей математике, 14-е изд., – М.: ООО «Большая медведица», АПП «Джангар», 2001, 864с.
2. Сивухин Д. В. Общий курс физики. Т.1. Механика. 5-е изд., стереот. – М.: ФИЗМАТЛИТ., 2010, 560с.
3. Шипов Г.И. Теория физического вакуума. Теория эксперименты и технологии. 2-е изд., – М.:Наука, 1996, 456с.
4. Ольховский И.И. Курс теоретической механики для физиков: Учебное пособие. 4-е изд., стер. – СПб.: Издательство «Лань», 2009, 576с.
5. Справочник по физике для инженеров и студентов вузов / Б.М.Яворский, А.А.Детлаф, А.К.Лебедев. – 8-е изд.,перераб. и испр. – М.: ООО «Издательство Оникс», «Издательство «Мир и Образование», 2008, 1056с.
6. Хайкин С.Э. Физические основы механики, 2-е изд., испр. и доп. Учебное пособие. Главная редакция физико-математической литературы. М.: Наука, 1971, 752с.
7. Зорич В.А. Математический анализ. Часть 1. Изд. 2-е, испр. и доп. М.: ФАЗИС, 1997, 554с.
8. Александров Н.В. и Яшкин А.Я. Курс общей физики. Механика. Учеб. пособие для студентов заочников физ.-мат. фак. пед. ин-тов. М., «Просвещение», 1978, 416с.
9. Геронимус Я. Л. Теоретическая механика (очерки об основных положениях): Главная редакция физико-математической литературы изд-ва «Наука», 1973г., 512с.
10. Курс теоретической механики: учебник / А.А.Яблонский, В.М.Никифорова. – 15-е изд., стер. – М.: КНОРУС, 2010, 608с.
11. Турышев М.В., О движении замкнутых систем, или при каких условиях не выполняется закон сохранения импульса, «Естественные и технические науки», №3(29), 2007, ISSN 1684-2626.
12. Айзерман М.А. Классическая механика: Учебное пособие. – 2-е изд., перераб. – М.: Наука. Главная редакция физико-математической литературы, 1980, 368с.
13. Яворский В.М., Пинский А.А. Основы физики: Учебн. В 2 т. Т.1. Механика, Молекулярная физика. Электродинамика / Под ред. Ю.И.Дика. – 5-е изд., стереот. – М.: ФИЗМАТЛИТ. 2003. – 576с.
14. Киттель Ч., Найт В., Рудерман М. Механика: Учебное руководство: Пер. с англ./Под ред. А.И.Шальникова и А.С.Ахматова. – 3-е изд., испр. – М.: Наука. Главная редакция физико-математической литературы. 1983. – (Берклеевский курс физики, Том 1). – 448с.
15. Толчин В. Н., Инерцоид, Силы инерции как источник поступательного движения. Пермь. Пермское книжное издательство, 1977, 99с.
16. Фролов А.В. Вихревой движитель, «Новая энергетика», №3 (18), 2004, ISSN 1684-7288.
17. Берников В.Р. Некоторые следствия из основного закона механики, «Журнал научных публикаций аспирантов и докторантов», №5 (71), 2012, ISSN 1991-3087.
18. Берников В.Р. Силы инерции и ускорение, «Научная перспектива», №4, 2012, ISSN 2077-3153.
19. Берников В.Р. Силы инерции и их применение, «Журнал научных публикаций аспирантов и докторантов», №11 (65), 2011, ISSN 1991-3087.
20. Меньшиков В.А., Дедков В.К. Тайны тяготения. – М.: НИИ КС, 2007. –332с.
http://helpiks.org/3-65393.html
http://jurnal.org/articles/2014/meh2.html