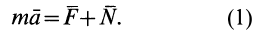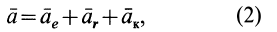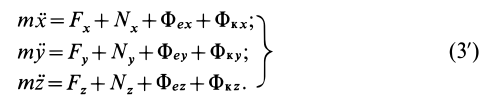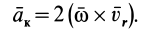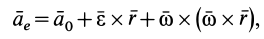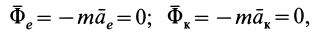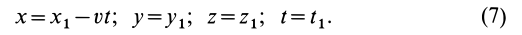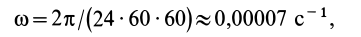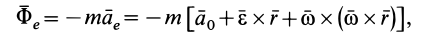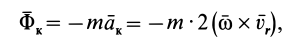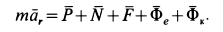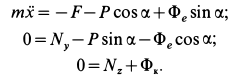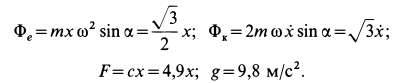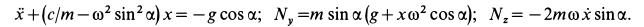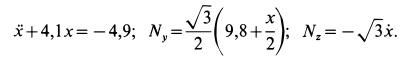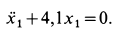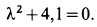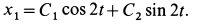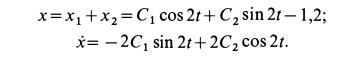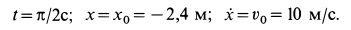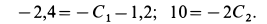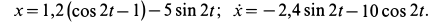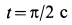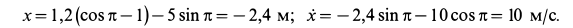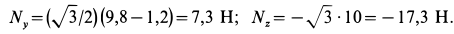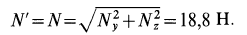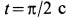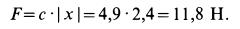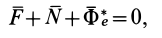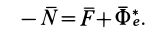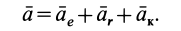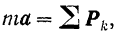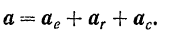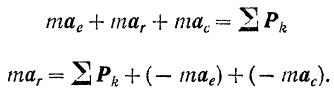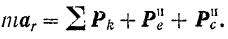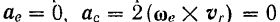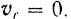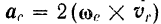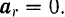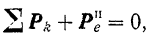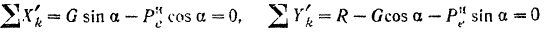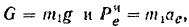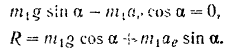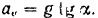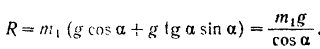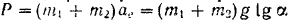Курсовая, реферат, контрольная – в чем же разница?
Относительное равновесие. Под относительным равновесием точки следует понимать отсутствие перемещения в подвижной системе координат, т.е. > ; , тогда уравнение относительного движения для несвободной точки
Это и уравнение относительного покоя. Из него видно, что в случае равновесия материальной точки заданная сила, реакция связи переносная сила инерции взаимно уравновешены.
4. Невесомость, под невесомостью материальной течки в какой-либо системе координат понимают отсутствие давления этой точки на тела, покоящиеся координат. Явление невесомости следует рассматривать для точки, находящейся относительном покое, т.е. > , но при невесомости получаем условие, при котором наступает невесомость
Например, если > , тo ; .
Подвижная система должна иметь ускорение, равное ускорению свободного падения.
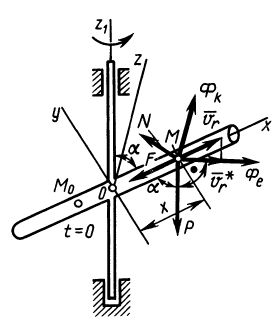
Пример. Кольцо М движется по гладкому стержню ОА = 1 м, который равномерно вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через конец О, делая 1 об/с (рис. 19). В момент t = 0 кольцо находилось на расстоянии ОМ = 60 см и начальной скорости не имело. Определить тот времени, когда сойдет со стержня.
Решение. 1. За переносное движение возьмем вращение стержня, за относительное — движение точки по стержню .
3. На точку девствует вес > , нормальная реакция со стороны стержня , но обе они ||Oz, т.е. перпендикулярны, их не изображаем на чертеже.
— вдоль стержня направлена, — перпендикулярна ему.
5. Дифференциальное уравнение в проекции на ось Ox1:
Найдем С1 и С2 — произвольные постоянные по начальным условиям:
Уравнение относительного движения кольца
; n=1 об/с; w =2 p с-1
Найдем тот момент времени, когда кольцо сойдет со стержня;
OM1=OA=100 см и x1=OM1=100 см;
(не удовлетворяет, так как );
Порядок решения примеров
1. Разложить абсолютное движение на составляющие — переносное и относительное.
2. Записать начальные условия относительного движения.
3. Изобразить силы, приложенные к точке.
4. Определить > и .
5. Составить дифференциальные уравнения относительного движения.
6. Проинтегрировать полученные дифференциальные уравнения.
Относительное движение материальной точки в теоретической механике
Содержание:
Относительное движение материальной точки:
Во многих задачах динамики рассматривается движение материальной точки относительно системы отсчета, движущейся относительно инерциальной системы. Дифференциальные уравнения движения материальной точки относительно таких подвижных, в общем случае неинерциальных, систем отсчета получают из уравнений движения точки относительно инерциальной системы отсчета и кинематической теоремы Кориолиса о сложении ускорений.
Имеем инерциальную систему отсчета
Рис. 14
Если ввести другую, неинерциальную, систему отсчета 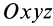
где 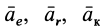
Подставляя значение абсолютного ускорения 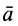
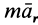
где 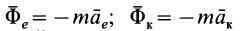
Силы инерции 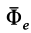
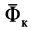
Если координаты движущейся точки относительно подвижной системы координат 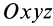
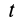
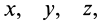
Это дифференциальные уравнения движения точки относительно подвижной системы координат в проекциях на декартовы подвижные оси координат. Они отличаются от дифференциальных уравнений абсолютного движения относительно инерциальной системы отсчета только наличием поправок на неинерциальность системы отсчета.
Относительное движение по инерции
Если материальная точка движется относительно подвижной системы отсчета прямолинейно и равномерно, то такое движение называют относительным движением по инерции. В этом случае относительная скорость 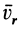
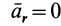
Это условие для сил при относительном движении точки по инерции.
Относительное равновесие
При покое материальной точки относительно подвижной системы отсчета ее относительные скорость и ускорение равны нулю, т. е. 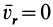
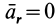
Из (3) получаем условие относительного равновесия для сил:
При абсолютном движении по инерции или абсолютном равновесии относительно инерциальной системы отсчета имеем для сил одно и то же условие 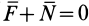
Инерциальные системы отсчета
Переносное ускорение в общем случае вычисляется по формуле
где 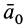
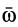
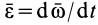
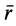
Пусть подвижная система отсчета все время движется относительно основной инерциальной системы поступательно, равномерно и прямолинейно. В этом случае переносная и кориолисова силы инерции равны нулю, т. е.
так как при поступательном движении 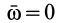
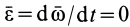
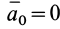
которое совпадает с уравнением движения относительно инерциальной системы отсчета (1).
Все подвижные системы отсчета, которые движутся поступательно, равномерно и прямолинейно относительно основной инерциальной системы отсчета, называются тоже инерциальными. Относительно всех инерциальных систем отсчета получаются одинаковые уравнения движения материальной точки. Ускорения материальной точки относительно всех инерциальных систем отсчета одинаковы.
Отсутствие принципиальной возможности каким-либо механическим опытом, основанным на наблюдении за движением материальных тел, отличить одну инерциальную систему отсчета от другой находится в основе принципа относительности классической механики — принципа Галилея — Ньютона, который утверждает: все механические явления в различных инерциальных системах отсчета протекают одинаково, или никаким механическим опытом нельзя обнаружить инерциальное движение системы отсчета, участвуя вместе с ней в этом движении. Наоборот, неинерциальную систему отсчета можно обнаружить и отличить одну от другой по поправкам на неинерциальность.
Скорости материальной точки относительно различных инерциальных систем отсчета разные, но нет возможности из наблюдений за движением материальной точки в различных системах отсчета сделать утверждение, какая из инерциальных систем отсчета является основной, неподвижной, а какая — подвижной.
В специальной теории относительности имеет место принцип относительности Эйнштейна, который утверждает: все физические явления во всех инерциальных системах отсчета протекают одинаково. Физические явления кроме механических включают также электромагнитные процессы.
Рис. 15
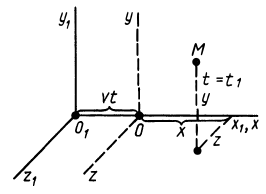
Возьмем две инерциальные системы отсчета: 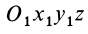
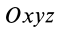
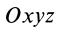
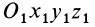
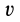
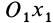
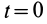
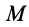
Эти соотношения называются преобразованиями Галилея в частном случае движения двух инерциальных систем отсчета друг относительно друга.
Преобразования Галилея не изменяют формы уравнения движения точки (1), т. е. оно инвариантно по отношению к преобразованиям Галилея.
Движение точки относительно земли
Для неинерциальной системы отсчета уравнение движения материальной точки под действием силы отличается от уравнения движения относительно инерциальных систем отсчета. Согласно (3), оно имеет форму
Наличие поправок на неинерциальность систем отсчета в виде сил инерции 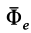
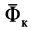
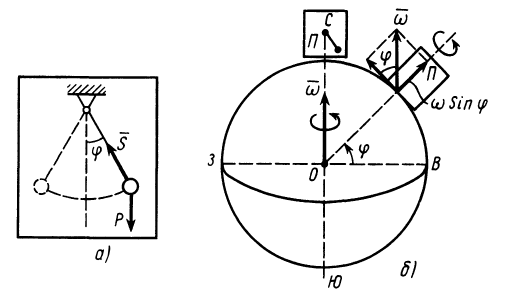
Система отсчета, скрепленная с земным шаром, не является инерциальной. Земной шар движется относительно гелиоцентрической инерциальной системы отсчета. При рассмотрении движения материальных тел относительно Земли должны проявлять себя эффекты, связанные с неинерциальностью системы отсчета. Земной шар движется относительно гелиоцентрической системы отсчета как свободное твердое тело. Его центр перемещается по эллиптической орбите, близкой к окружности. Кроме того, он вращается вокруг оси, проходящей через его центр, с почти постоянной по модулю и направлению угловой скоростью, совершая один оборот за сутки. Угловая скорость вращения Земли
т. е. величина малая по сравнению с единицей.
В общем случае переносная сила инерции
где 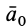
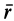
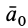
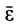
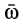
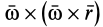
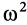
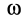
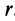
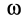
где 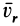
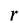
Маятник Фуко
Если подвесить на длинной нити груз достаточно малых размеров, то действующая на него сила 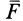
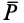
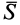
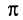
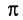
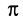
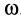
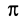
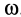
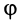
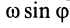
Рис. 16
Рис. 17
Если тело маятника имеет выступ, который при колебаниях может оставлять след, например на песке, то этот след при движении маятника в одну сторону будет отличаться от следа при движении в противоположную сторону из-за вращения Земли. Это отличие тем больше, чем длиннее нить маятника. Фуко в 1857 г. использовал маятник длиной 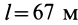
Отклонение движущихся тел вправо в Северном полушарии
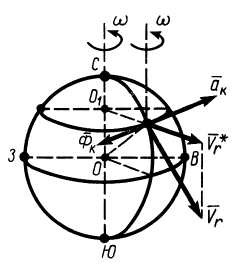
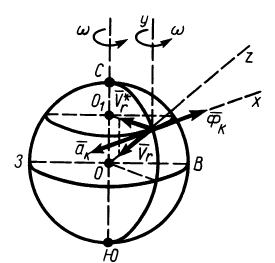
В Северном полушарии из-за дополнительного действия силы инерции Кориолиса, вызванной вращением Земли, все движущиеся тела должны смещаться в правую сторону, если смотреть в направлении движения. Пусть материальная точка движется со скоростью 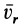
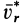
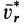
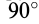
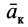
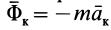
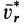
Если рассмотреть поступательное движение железнодорожного вагона, то для него сила инерции Кориолиса пройдет через центр его тяжести слева направо, если смотреть по движению вагона. Это приведет к увеличению давления на правый рельс и к его уменьшению на левый. На двухколейных железных дорогах правый рельс изнашивается быстрее левого.
Для частички воды в реке действие силы Кориолиса слева направо, если смотреть по течению реки, приведет к прижиманию этой частички к правому берегу, способствуя большему его подмыванию. Правый берег рек в Северном полушарии более подмыт, чем левый на прямолинейных участках реки. Этот эффект известен в географии как закон Бэра. На закруглениях реки вследствие центробежных сил инерции может оказаться подмытым и левый берег.
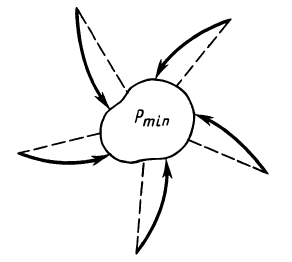
Действие силы инерции Кориолиса на летящие самолеты, ракеты, снаряды, движущийся воздух, морские течения приводит к их отклонению в правую сторону в Северном полушарии. В Южном полушарии отклонение будет в левую сторону. Сила инерции Кориолиса способствует образованию циклонов, антициклонов, вихрей, смерчей и т. д. Если в каком-то месте образовалось пониженное давление, например вследствие местного нагревания воздуха, то к этому месту начнет двигаться воздух из мест с повышенным давлением. Сила инерции Кориолиса отклонит движущиеся частички воздуха вправо, создав местный вихрь (рис. 18), а для больших масс воздуха— циклон. Аналогично, в местах с повышенным давлением образуются антициклоны.
Отклонение падающих тел к востоку
Рассмотрим в Северном полушарии тело, падающее вертикально вниз под действием силы тяжести без начальной скорости. Действие силы инерции Кориолиса в этом случае в первом приближении сведется к отклонению падающего тела к востоку. Действительно, если скорость тела 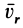
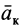
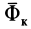
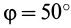
Пример:
Внутри трубки, имеющей гладкую поверхность, находится шарик массой 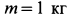
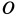
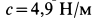
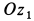
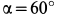
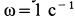
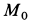
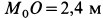
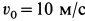
Определить закон движения шарика по трубке, принимая его за точку; силу давления шарика на стенку трубки и силу притяжения в момент времени 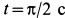
Решение:
Выберем систему подвижных осей координат 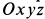
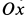
Векторное уравнение движения шарика относительно подвижной системы координат имеет вид
В проекциях на подвижные оси координат
Здесь 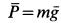
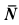
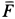
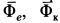
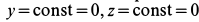
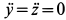
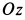
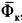
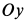
Подставляя эти значения сначала в общем виде в уравнения движения, после простых преобразований получаем:
После подстановки числовых значений величин имеем
Дифференциальное уравнение является линейным неоднородным; следовательно, его решение
где 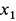
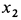
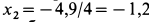
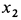
Общее решение однородного уравнения 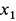
Его характеристическое уравнение
Корни характеристического уравнения 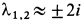
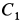
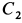
Начальные условия задачи
Подставляя их в выражения для 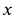
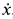
Их решения 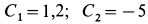
Уравнения движения шарика с учетом значений постоянных принимает вид
В момент времени
Подставляя эти значения 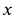
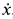
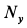
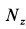
Давление шарика 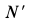
Сила притяжения 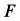
Невесомость
Динамическая теорема Кориолиса позволяет рассмотреть состояние невесомости, которое, в частности, возникает при движении космических кораблей как искусственных спутников Земли. При рассмотрении невесомости материальной точки целесообразно ее представлять как твердое тело, имеющее поверхность, которой оно может соприкасаться с другими телами. Будем предполагать, что скорости и ускорения всех точек тела одинаковы, а реакции соприкасающихся тел приводятся к равнодействующей.
Под невесомостью такой материальной точки понимают отсутствие давления этой точки на каждое из тел, с которым она может соприкасаться. В частности, невесомая материальная точка не давит на площадку весов (не имеет веса), находящихся в покое по отношению к той системе отсчета, относительно которой покоится материальная точка.
Систему отсчета, относительно которой материальная точка находится в покое и, следовательно, имеет относительно нее скорость и ускорение, равные нулю, назовем собственной системой отсчета материальной точки. Все величины относительно этой системы отсчета условимся обозначать специальным индексом 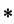
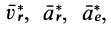
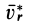
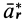
Невесомая материальная точка (тело), прикрепленная на пружине к любому телу, покоящемуся относительно ее собственной системы отсчета, не деформирует эту пружину. Учитывая, что давление точки на какое-либо тело по модулю совпадает с силой реакции тела на эту точку, невесомость наблюдается при равенстве нулю силы реакции от любого тела, соприкасающегося с рассматриваемой невесомой материальной точкой.
Если в общем случае рассматривать невесомость материального тела, а не точки, то реакции окружающих его тел сведутся к распределенным силам по поверхности его соприкосновения с этими телами. Сила реакции, отнесенная к единице площади поверхности соприкосновения (напряжение силы реакции), должна при невесомости тела быть равна нулю в каждой точке его поверхности. Это является условием невесомости для любого тела, не обязательно твердого.
Для абсолютно твердого тела при его невесомости вместо равенства нулю напряжения поверхностной силы в каждой точке его поверхности соприкосновения достаточно равенства нулю главного вектора и главного момента этих сил относительно любого центра приведения.
Ограничимся рассмотрением невесомости материальной точки, т. е. абсолютно твердого тела, для которого все поверхностные силы приводятся только к одной равнодействующей силе — реакции тел, соприкасающихся с ним. Невесомость материальной точки не связана с системой отсчета или с наблюдателем, находящимся в той или иной системе отсчета. Но для выявления сил, действие которых испытывает материальная точка, выберем ее собственную систему отсчета, по отношению к которой ее относительные скорость и ускорение равны нулю, т. е. 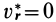
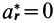
где 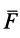
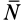
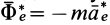
Из условия относительного равновесия сил имеем
Согласно определению невесомости, 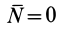
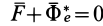
Таким образом, условие невесомости через силы можно выразить как 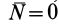
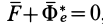
Согласно теореме о сложении ускорений, абсолютное ускорение в общем случае определяется по формуле
Если абсолютное ускорение рассматривать относительно инерциальной системы отсчета, а в качестве подвижной системы отсчета выбрать собственную систему отсчета, то 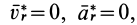
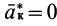
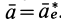
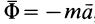
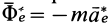
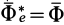
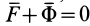
Проверим выполнение условия невесомости для материальной точки, находящейся в космическом корабле, который движется поступательно относительно Земли в качестве ее искусственного спутника за пределами атмосферы. За инерциальную систему отсчета можно принять систему отсчета, скрепленную с Землей.
Пусть материальная точка неподвижна относительно космического корабля. Тогда собственной системой отсчета будет система отсчета, скрепленная с кораблем. Силой от действия тел, не соприкасающихся с точкой, является сила тяготения Земли 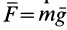
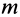
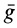
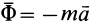
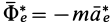
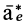
Если корабль не испытывает действия других сил, кроме силы тяготения Земли, то его ускорение от этого тяготения тоже равно 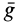
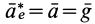
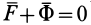
В космическом корабле, который кроме поступательного движения имеет также и вращение, каждая из материальных частиц корабля не находится в состоянии невесомости, хотя весь корабль как целое находится в состоянии невесомости. Для него главный вектор и главный момент поверхностных сил равны нулю, так как нет тел, с которыми корабль соприкасается своей поверхностью.
Материальная точка внутри кабины корабля находится в состоянии невесомости, пока она не соприкасается со стенками корабля и с другими телами, скрепленными с кораблем.
Кажется, что для невесомости тела необходима невесомость каждой его точки. Это приводит к требованию отсутствия взаимных давлений между точками тела или к отсутствию внутренних напряжений в теле. Но такие напряжения всегда имеются при невесомости вследствие естественной связи точек тела друг с другом, на которую можно влиять, например, термообработкой, изменением температуры и т. д. При невесомости тела как целого не обязательно отсутствие даже дополнительных напряжений, создаваемых движением тела. Достаточно равенства нулю напряжений в точках поверхности тела, создаваемых другими, соприкасающимися телами (связями), а для абсолютно твердого тела — равенства нулю главного вектора и главного момента поверхностных сил.
В невесомости находятся земной шар и другие планеты Солнечной системы, их спутники, если пренебречь действием на них метеоритов, космического излучения и т. д.
В состоянии невесомости находилось бы свободно падающее тело вблизи Земли, если бы не было действия воздуха. Невесомость можно создать искусственно вблизи Земли в герметизированной кабине летательного аппарата, заставив его с помощью двигателей совершать поступательное движение с ускорением 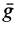
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Геометрия масс
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Основное уравнение динамики для относительного движения материальной точки
Основное уравнение динамики для относительного движения материальной точки
Основное уравнение динамики точки верно лишь по отношению к абсолютному движению точки, т. е. к ее движению относительно инерциальной системы отсчета.
Пусть требуется по заданным силам, действующим на материальную точку, определить ее относительное движение, т.е. движение точки по отношению к системе отсчета, которая сама совершает произвольное, но известное нам движение относительно инерциальной системы отсчета. Для решения этой задачи можно было бы поступить следующим образом: по заданным силам, действующим на данную материальную точку, определить сначала ее абсолютное движение, т. е. решить вторую задачу динамики, а затем, зная абсолютное и переносное движения точки, определить, по установленным в кинематике правилам, искомое относительное движение точки.
Существует, однако, формальный прием, позволяющий данную задачу решить значительно проще.
Согласно основному уравнению динамики для абсолютного движения точки имеем:
где 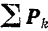
Из кинематики (§ 57) известно, что при произвольном переносном движении абсолютное ускорение 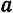
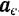
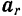
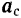
Подставляя это выражение абсолютного ускорения в основное уравнение динамики, будем иметь:
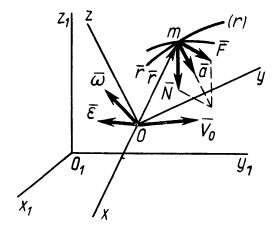
Стоящие в правой части последнего уравнения векторы — 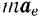
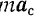
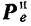
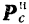
Вектор 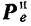
Вектор 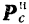
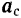
Подставив обозначения этих векторов в уравнение (II), получим:
Присоединение к активным силам и реакциям свя-I!сii переносной и кориолисовой сил инерции учитывает влияние перемещения подвижной системы отсчета на относительное движение точки.
Рассмотрим некоторые частные случаи.
- Подвижная система отсчета движется поступательно. прямолинейно и равномерно.
и потому переносная 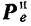
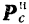
Такая система отсчета является, как об этом уже было сказано выше (стр. 236), инерциальной.
Связь между силами, действующими на точку, и ее движением по отношению к такой системе отсчета не зависит от того, находится ли эта система в покос по отношению к «неподвижной» или движется относительно нее поступательно, прямолинейно и равномерно.
Отсюда вытекает установленный еще Галилеем принцип относительности классической механики:
никакие механические явления не могут обнаружить, находится ли данная система в покое или движется поступательно, прямолинейно и равномерно.
- Точка находится в положении относительного равновесия. т. е. не совершает движения относительно подвижной системы отсчета.
Следовательно, равны нулю кориолисово ускорение точки
и кориолисова сила инерции
Равно нулю также и относительное ускорение точки
Таким образом, в случае относительного равновесия точки уравнение (113) принимает вид
т.е. должна равняться нулю геометрическая сумма: сил, действующих на нее со стороны других тел, и ее переносной силы инерции.
Пример задачи:
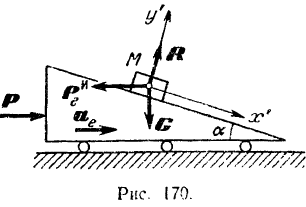
Тело массы 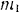
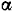
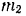
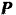
Решение:
Рассматриваем поступательно движущееся тело как материальную точку 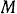
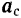
На точку 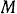
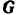
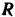
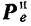
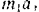
Связав с движущимся телом координатные оси 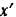
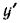
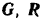
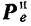
или. подставляя в эти уравнения значения
Из уравнения (1) определяем переносное ускорение
Подставляя это значение в уравнение (II), находим нормальную реакцию плоскости, а следовательно, и силу давления тела на плоскость:
Так как наклонная плоскость вместе с находящимся па ней телом должна двигаться по неподвижной горизонтальной плоскости с ускорение то, при отсутствии сопротивления этому движению, искомая сила
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Возможно вам будут полезны эти дополнительные темы:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://www.evkova.org/otnositelnoe-dvizhenie-materialnoj-tochki-v-teoreticheskoj-mehanike
http://lfirmal.com/osnovnoe-uravnenie-dinamiki-dlya-otnositelnogo-dvizheniya-materialnoj-tochki/