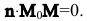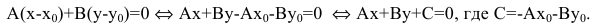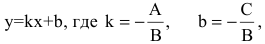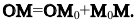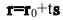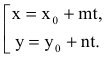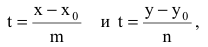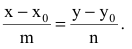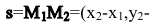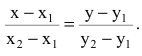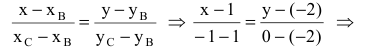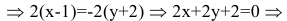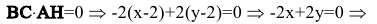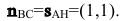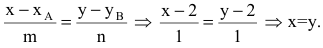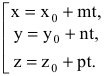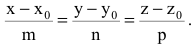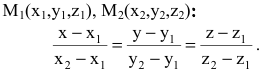Уравнение прямой
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
| x | + | y | = 1 |
| a | b |
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x — x 1 | = | y — y 1 |
| x 2 — x 1 | y 2 — y 1 |
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
где N( x 0, y 0) — координаты точки лежащей на прямой, a = < l , m >— координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a =
| x — x 0 | = | y — y 0 |
| l | m |
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x — 1 2 — 1 = y — 7 3 — 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1 y = -4 t + 7
Решение. Так как M y — N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x — x 1 | = | y — y 1 | = | z — z 1 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 | x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) — координаты точки лежащей на прямой,
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n =
| x — x 0 | = | y — y 0 | = | z — z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
Уравнение прямой в отрезках: описание, примеры, решение задач
Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.
Уравнение прямой в отрезках – описание и примеры
Пусть на плоскости расположена прямоугольная система координат O x y .
Прямая линия на плоскости в декартовой системе координат O x y задается уравнением вида x a + y b = 1 , где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях O x и O y . Длины отрезков считаются от начала координат.
Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a , 0 и 0 , b принадлежат данной прямой линии, так как a a + 0 b = 1 ⇔ 1 ≡ 1 и 0 a + b b = 1 ⇔ 1 ≡ 1 . Точки a , 0 и b , 0 расположены на осях координат O x и O y и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b . Знак « — » обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.
Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат O x y на схематическом чертеже. Уравнение прямой в отрезках x a + y b = 1 применяется для построения прямой линии в декартовой системе координат O x y . Для этого нам необходимо отметить на осях точки a , 0 и b , 0 , а затем соединить эти точки линией при помощи линейки.
На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.
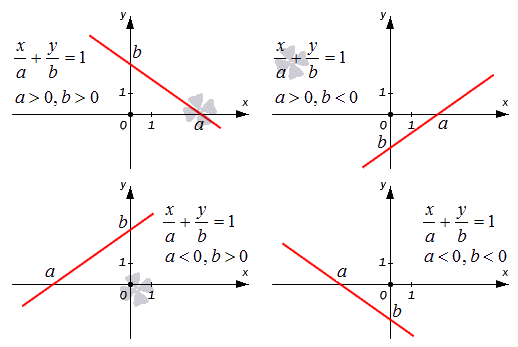
Прямая линия задана уравнением прямой в отрезках вида x 3 + y — 5 2 = 1 . Необходимо построить эту прямую на плоскости в декартовой системе координат O x y .
Решение
Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3 , 0 , 0 , — 5 2 . Отметим их и проведем линию.
Приведение общего уравнения прямой к уравнению прямой в отрезках
Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.
Полное общее уравнение прямой линии на плоскости имеет вид A x + B y + C = 0 , где А , В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на – С . При этом, коэффициенты при x и y мы отправляем в знаменатели:
A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1
Для осуществления последнего перехода мы воспользовались равенством p q = 1 q p , p ≠ 0 , q ≠ 0 .
В результате, мы осуществили переход от общего уравнения прямой A x + B y + C = 0 к уравнению прямой в отрезках x a + y b = 1 , где a = — C A , b = — C B .
Разберем следующий пример.
Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x — 7 y + 1 2 = 0 .
Решение
Переносим одну вторую в правую часть равенства x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .
Делим обе части равенства на — 1 2 : x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .
Преобразуем полученное равенство к нужному виду: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .
Мы получили уравнение прямой в отрезках.
Ответ: x — 1 2 + y 1 14 = 1
В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.
Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида x a + y b = 1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y .
x a + y b = 1 ⇔ x a + y b — 1 = 0 ⇔ 1 a · x + 1 b · y — 1 = 0
Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».
Уравнение прямой в отрезках имеет вид x 2 3 + y — 12 = 1 . Необходимо написать общее уравнение прямой на плоскости.
Решение
Действует по заранее описанному алгоритму:
x 2 3 + y — 12 = 1 ⇔ 1 2 3 · x + 1 — 12 · y — 1 = 0 ⇔ ⇔ 3 2 · x — 1 12 · y — 1 = 0
Ответ: 3 2 · x — 1 12 · y — 1 = 0
Прямая — понятие, виды и её свойства с примерами
Содержание:
Прямая:
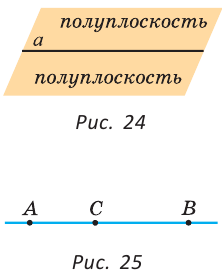
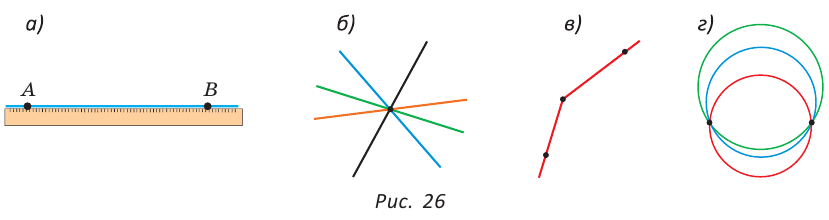
Прямая бесконечна (в обе стороны) и разбивает плоскость на две полуплоскости (рис. 24), для которых прямая является границей. Граница принадлежит полуплоскостям. На рисунке 25 точка С лежит на прямой между точками А и В, которые лежат по разные стороны от точки С. Точки С и В лежат по одну сторону от точки А. Из трех точек на прямой одна и только одна точка лежит между двумя другими.
Если на плоскости отметить две точки А и В, то через них всегда можно провести прямую АВ (рис. 26, а). Через одну точку можно провести бесконечно много прямых (рис. 26, б), через три точки не всегда можно провести прямую (рис. 26, в). Через две точки можно провести бесконечно много окружностей (рис. 26, г), а прямую — только одну!
Аксиома прямой. Через любые две точки плоскости можно провести прямую, и притом только одну.
Из аксиомы следует, что если две прямые (
Определение. Две прямые называются пересекающимися, если они имеют общую точку.
Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Если прямые 
Луч:
Определение. Лучом называется часть прямой, ограниченная одной точкой.
Точка, ограничивающая луч, принадлежит лучу и называется началом луча. Луч бесконечен (в одну сторону). Он обозначается одной малой буквой, или двумя большими буквами, где первой всегда записывается начало луча.
При этом вторая точка может быть не отмечена на луче. Она указывает направление луча, например как точка В на луче АВ (рис. 29).
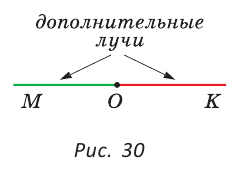
Определение. Два луча называются дополнительными (противоположными), если они имеют общее начало и лежат на одной прямой.
На рисунке 30 изображены дополнительные дополнительные лучи ОМ и ОК. Они дополняют друг друга до прямой. Чтобы построить луч, дополнительный данному, достаточно продлить данный луч за его начало вдоль прямой, на которой лежит данный луч. Любая точка прямой разбивает ее на два дополнительных луча.
Отрезок:
Определение. Отрезком называется часть прямой, ограниченная двумя точками.
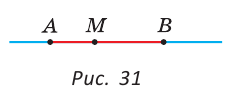
Точки, ограничивающие отрезок, принадлежат отрезку и называются концами отрезка, остальные точки отрезка — его внутренними точками. На рисунке 31 изображен отрезок АВ с концами А и В. Точка М — внутренняя точка отрезка АВ.
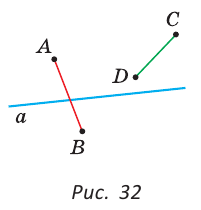
Если концы отрезка лежат в разных полуплоскостях относительно прямой, то этот отрезок пересекает прямую, если в одной полуплоскости — то не пересекает. На рисунке 32 концы отрезка АВ лежат в разных полуплоскостях относительно прямой а, и он пересекает прямую 
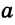
Если при наложении отрезков их концы совпадут, то по аксиоме прямой эти отрезки совпадут всеми своими точками.
Определение. Два отрезка называются равными, если их можно совместить наложением.
Важной характеристикой отрезка является его длина.
Свойства длины отрезка: каждый отрезок имеет длину, выраженную положительным числом; равным отрезкам соответствуют равные длины, большему отрезку — большая длина. И наоборот.
Аксиома измерения отрезков. Если на отрезке взять точку, то она разобьет данный отрезок на два отрезка, сумма длин которых равна длине данного отрезка.
Аксиома откладывания отрезков. На любом луче от его вершины можно отложить отрезок данной длины, и притом только один.
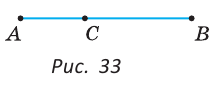
На рисунке 33 точка С лежит на отрезке АВ. По аксиоме измерения отрезков следует, что АС + СВ=АВ.
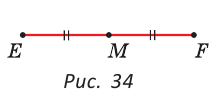
Серединой отрезка называется точка, которая делит отрезок на два равных отрезка. На рисунке 34 точка М — середина отрезка EF, то есть ЕМ = MF.
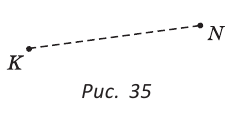
Определение. Расстоянием между двумя точками называется длина отрезка, соединяющего эти точки.
На рисунке 35 расстояние между точками К и N равно длине отрезка KN.
Ломаная:
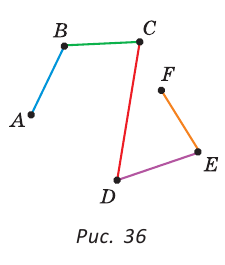
На рисунке 36 отрезки АВ, ВС, CD, DE и EF последовательно соединены своими концами: отрезок ВС соединен с отрезком АВ, отрезок CD соединен с отрезком ВС и так далее. Полученная фигура представляет собой ломаную ABCDEF. Указанные отрезки называются звеньями ломаной, а точки А, В, С, D, Е и F — вершинами ломаной.
Определение. Ломаной называется геометрическая фигура, образованная отрезками, последовательно соединенными своими концами, у которой никакие два соседних звена не лежат на одной прямой. Длиной ломаной называется сумма длин ее звеньев.
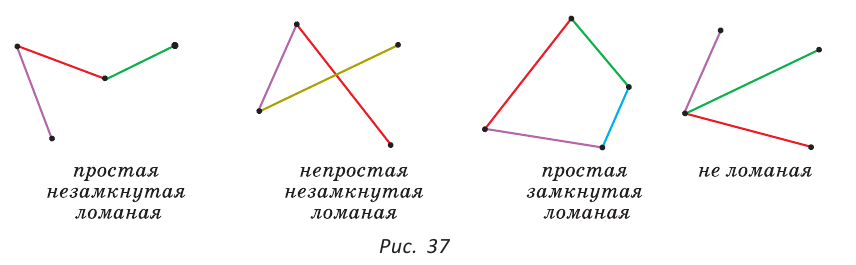
Определение. Ломаная называется замкнутой, если начало ее первого звена совпадает с концом последнего. В противном случае она называется незамкнутой. Ломаная называется простой, если она не имеет самопересечений и никакие два ее звена, кроме соседних, не имеют общих точек. В противном случае она называется непростой (рис. 37).
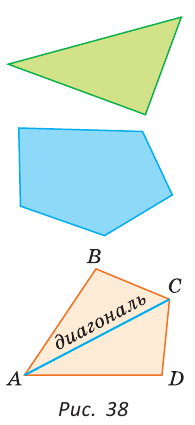
Простая замкнутая ломаная на плоскости называется многоугольником. Звенья этой ломаной называются сторонами этого многоугольника, а вершины — вершинами многоугольника. Периметром многоугольника называется сумма длин его сторон. Часть плоскости, ограниченная многоугольником, называется плоским многоугольником. Слово «плоский» употреблять не будем. Отрезок, соединяющий вершины многоугольника, не принадлежащие одной стороне, называется его диагональю. Если у многоугольника три стороны, то у него три вершины и три угла, и он называется треугольником, если четыре стороны — четырехугольником, если пять — пятиугольником и так далее.
На рисунке 38 изображен четырехугольник ABCD со сторонами АВ, ВС, CD и AD. У него четыре угла: 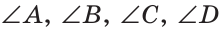
При записи многоугольника его вершины записываются последовательно, начиная с любой вершины и в любом направлении. Например, СBAD — это тот же четырехугольник ABCD.
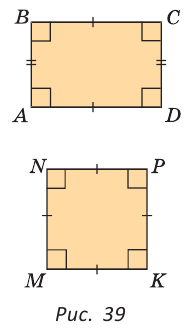
Самые известные четырехугольники — это прямоугольник и квадрат. У прямоугольника все углы прямые, а противоположные стороны равны. Квадрат — это прямоугольник, у которого все стороны равны. На рисунке 39 ABCD — прямоугольник, MNPK — квадрат. Позже мы дадим определение прямоугольника и квадрата и рассмотрим их свойства подробно. А пока будем пользоваться указанными представлениями.
Пример:
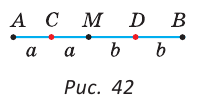
На отрезке АВ, равном 24 см, взята точка С. Отрезок АС на 6 см больше отрезка СВ. Найти длину отрезка АС.
Решение:
Пусть СВ = 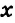
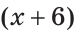
По аксиоме измерения отрезков 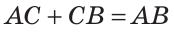
То есть, 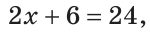
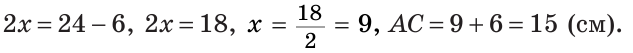
Ответ: 15 см.
Замечание. В дальнейшем при решении задач не будем ссылаться на аксиому измерения отрезков.
Пример:
На отрезке АВ отмечены точки С и D (рис. 41). Найти длину отрезка CD, если:
Решение:
Ответ: а) 6 см; б)
Пример:
На отрезке АВ, равном 42 см, взята точка М. Найти расстояние между серединами отрезков AM и MB.
Решение:
Пусть С — середина отрезка AM, D — середина отрезка MB.
Обозначим 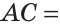
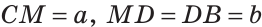
Тогда
Следовательно, 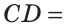
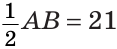
Замечание. В данной задаче мы доказали свойство: «Если на отрезке отмечена точка, то расстояние между серединами полученных отрезков равно половине данного отрезка». Утверждения, которые будут доказаны нами в ключевых задачах, могут в дальнейшем использоваться как известные свойства.
Прямая в высшей математике
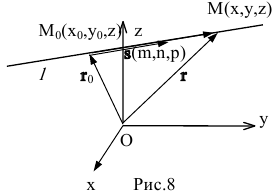
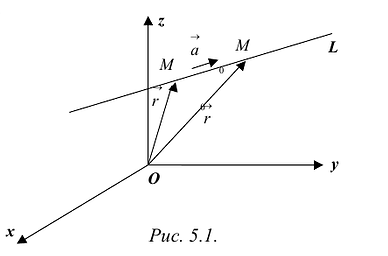
Прямая L в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой). Пусть задана такая точка 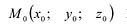
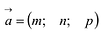
Если М(х, у, z) — произвольная текущая точка прямой L, то вектор 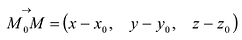
Этим соотношениям удовлетворяют координаты любой точки прямой L и только этой прямой. Равенства (5.1) называются каноническими уравнениями прямой в пространстве.
Обозначим 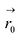
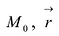
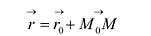
В силу коллинеарности векторов 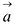
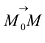
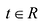
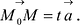
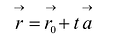
В координатной форме уравнение (5.3) равносильно трем уравнениям:
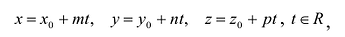
которые называются параметрическими уравнениями прямой в пространстве.
Исключая из уравнений (5.4) параметр t, легко перейти к каноническим уравнениям прямой (5.1).
Обратный переход от (5.1) к (5.4) осуществляют, приравнивая каждое из трех соотношений (5.1) к t. При этом, если знаменатель какого-либо соотношения равен нулю, то необходимо приравнять к нулю его числитель.
Пусть заданы точки 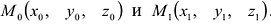
Очевидно, что в этом случае направляющим вектором прямой L будет вектор 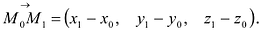
Прямую L в пространстве можно определить как пересечение двух плоскостей. Рассматривая совместно уравнения этих плоскостей, получим уравнение линии L в общем виде:
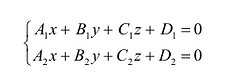
Система двух уравнений первой степени (5.6) определяет прямую линию при условии, что нормальные векторы 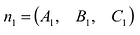
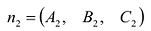
Чтобы перейти от общих уравнений прямой (5.6) к ее каноническим уравнениям (5.1), нужно на прямой найти какую-нибудь точку 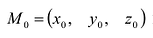
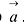
Точку 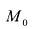
Направляющий вектор 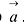
Поэтому в качестве 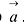
Понятие прямой
Нормальным вектором прямой называется любой вектор, перпендикулярный прямой.
Направляющим вектором прямой называется любой вектор, лежащий на этой прямой.
Взаимное расположение прямых
Пусть даны две прямые:
Эти прямые заданы своими точками 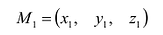
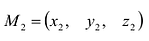
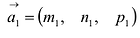
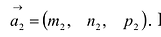
Параллельность или перпендикулярность прямых равносильна, соответственно, параллельности или перпендикулярности их направляющих векторов. Поэтому условие перпендикулярности прямых можно записать в виде:
Условие параллельности:
Возможны четыре случая взаимного расположения прямых:
- I. Прямые совпадают
, т.е.
- II. Прямые параллельны:
непараллелен
,
- III. Прямые пересекаются:
непараллелен
,
— компланарны, т.е.
- IV. Прямые скрещиваются:
— некомпланарны, т.е.
.
Условие (5.8) выполняется в случаях I-III и означает, что прямые лежат в одной плоскости.
Уравнения прямой на плоскости
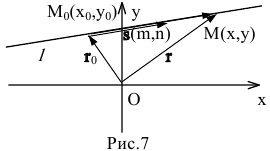
1. Па плоскости Оху составим уравнение прямой l, проходящей через точку 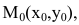
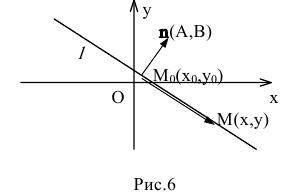
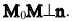
В координатной форме это равенство примет вид:
Уравнение Ах+Ву+С=0, где А и В не равны одновременно нулю 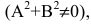
Если 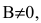
притом 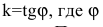
Вывод. Прямая на плоскости однозначно определяется точкой и нормальным вектором.
2. Па плоскости Оху составим уравнение прямой l, проходящей через точку 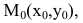
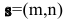
Пусть М(х,у) — произвольная точка прямой l, 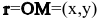
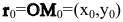
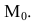
Так как векторы 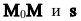
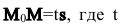
или в координатной форме параметрические уравнения прямой:
Пусть m и n отличны от нуля. Разрешим каждое из уравнений относительно t:
откуда получаем каноническое уравнение прямой:
Пусть прямая l проходит через две точки 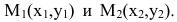
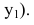
Вывод. Прямая однозначно определяется точкой и направляющим вектором.
Пример:
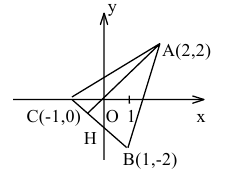
Вершины треугольника находятся в точках А(2,2), В(1,-2), С(-1,0). Найти проекцию точки А на основание ВС.
Решение:
Проекция точки А на ВС есть точка пересечения основания ВС с перпендикуляром, опущенным из А на ВС.
Составим уравнение прямой ВС по двум точкам:
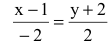
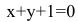
Обозначим искомую проекцию точкой Н(х,у). Т.к. 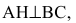
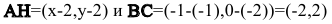
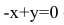
Теперь найдем проекцию точки А на основание ВС. Для этого решим систему: 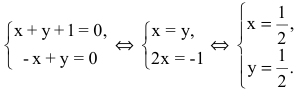
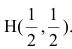
Замечание. Уравнение прямой АН можно было находить другими способами. Например, из общего уравнения прямой ВС х+у+1=0 можно выписать координаты нормального вектора 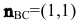
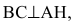
По нормальному вектору 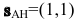
Уравнения прямой в пространстве
Уравнения прямой l, проходящей через точку 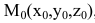
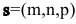
Пусть M(x,y,z) — произвольная точка прямой 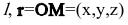
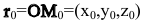
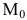
Тогда векторное уравнение прямой останется прежним: 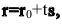
Параметрические уравнения прямой примут вид:
В случае 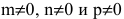
Наконец, составим уравнения прямой, проходящей через две точки
Внимание! В пространстве точка и нормальный вектор однозначным образом определяют плоскость. Поэтому в пространстве общие уравнения прямой будут задаваться линией пересечения двух плоскостей.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоскость — определение, виды и правила
- Кривые второго порядка
- Евклидово пространство
- Матрица — виды, операции и действия с примерами
- Корень из числа — нахождение и вычисление
- Теория множеств — виды, операции и примеры
- Числовые множества
- Вектор — определение и основные понятия
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-prjamoj-v-otrezkah/
http://www.evkova.org/pryamaya





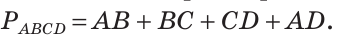
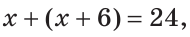
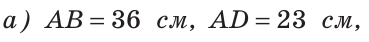
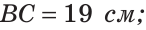
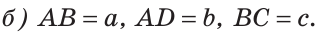
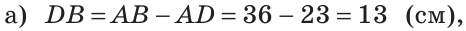
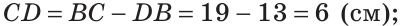
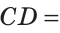
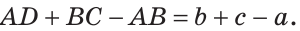
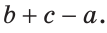
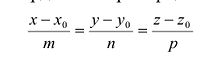
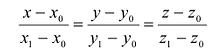
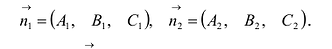
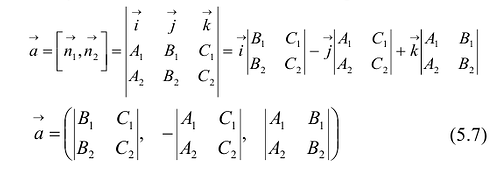
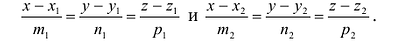
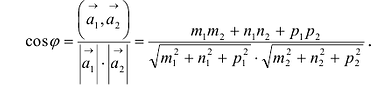
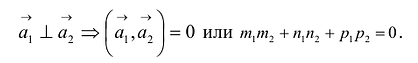
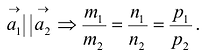
 , т.е.
, т.е. 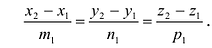
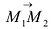 непараллелен
непараллелен 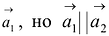 ,
, 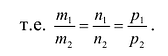
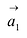 непараллелен
непараллелен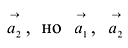 ,
, 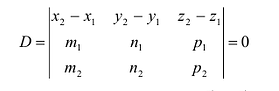
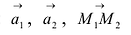 — некомпланарны, т.е.
— некомпланарны, т.е. 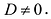 .
.