Уравнение параболоида в сферических координатах

Примеры применения цилиндрических и сферических координат

Примеры применения цилиндрических и сферических координат

1. Услуги проектирования
2. Тройной интеграл
3. Примеры применения цилиндрических и сферических координат

Примеры применения цилиндрических и сферических координат

Как и в случае перехода к полярным координатам в двойном интеграле, дать однозначный рецепт того, когда следует применять цилиндрические или сферические координаты, нельзя, это дело опыта. Можно попробовать применить цилиндрические координаты, если подынтегральная функция и/или уравнения поверхностей, ограничивающих объём $\mathbf < \textit < V >> $, зависят от комбинации $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >=\mathbf < \textit < r >> ^ < 2 >$; сферические — если эти уравнения зависят от $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >+\mathbf < \textit < z >> ^ < 2 >=\mathbf < \textit < r >> ^ < 2 >$. Рассмотрим ряд примеров.

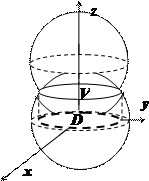
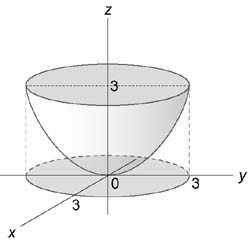
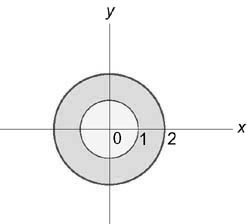
Найти объём $\mathbf < \textit < V >> $ общей части двух шаров, ограниченных сферами

Решение:

Пересечение сфер находится на уровне $2Rz=R^2\Rightarrow z=R/2$ и представляет собой круг радиуса $R\frac < \sqrt 3 > < 2 >$. Объём $\mathbf < \textit < V >> $ограничен сверху поверхностью $z=\sqrt < R^2-x^2-y^2 >$, снизу — поверхностью $z=R-\sqrt < R^2-x^2-y^2 >$. Вычисления в декартовых координатах дают $V=\iiint\limits_V < dv >=\iiint\limits_V < dxdydz >=\int\limits_ < -R\frac < \sqrt 3 > < 2 >> ^ < R\frac < \sqrt 3 > < 2 >> < dx\int\limits_ < -\sqrt < \frac < 3 > < 4 >R^2-x^2 > > ^ < \sqrt < \frac < 3 > < 4 >R^2-x^2 > > < dy\int\limits_ < R-\sqrt < R^2-x^2-y^2 >> ^ < \sqrt < R^2-x^2-y^2 >> < dz >> > $ — достаточно громоздкие выкладки.

В цилиндрических координатах объём $\mathbf < \textit < V >> $ ограничен сверху поверхностью $z=\sqrt < R^2-r^2 >$, снизу — поверхностью $z=R-\sqrt < R^2-r^2 >$, поэтому

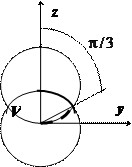
В сферических координатах уравнение нижней сферы принимает вид $r=R$, верхней — $r^2=2Rr\cos \theta \Rightarrow r=2R\cos \theta $, их пересечение соответствует значению $\cos \theta =1/2\Rightarrow \theta =\pi /3$. В интервале $0\leqslant \theta \leqslant \pi /3 \quad \mathbf < \textit < r >> $ меняется от $0$ до $\mathbf < \textit < R >> $, в интервале $\pi /3\leqslant \theta \leqslant \pi /2 \quad \mathbf < \textit < r >> $ меняется от $0$ до $2R\cos \theta $, поэтому

В этом примере трудоёмкость вычислений в цилиндрических и сферических координатах примерно одинакова.

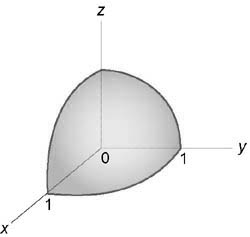
Решение:

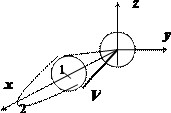
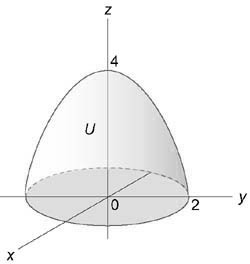
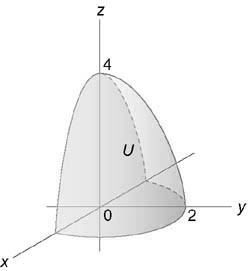
Параболоид и конус пересекаются в плоскости $x=2-x^2\Rightarrow x=1$ по кругу радиуса 1. Осью симметрии объёма $\mathbf < \textit < V >> $ служит ось $\mathbf < \textit < Ох >> $, поэтому цилиндрические координаты вводим формулами $x=x,\quad y=r\cos \varphi ,\quad z=r\sin \varphi ; \quad I=\iiint\limits_V < (x+y+z)dxdydz >=\iiint\limits_V < (x+r\cos \varphi +r\sin \varphi )rdxdrd\varphi >=\int\limits_0^ < 2\pi > < d\varphi \int\limits_0^1 < rdr\int\limits_r^ < 2-r^2 > < (x+r\cos \varphi +r\sin \varphi )dx >> > =$ $ =\int\limits_0^ < 2\pi > < d\varphi \int\limits_0^1 < \left. < \frac < x^2 > < 2 >>\right|_r^ < 2-r^2 >rdr > > +\int\limits_0^ < 2\pi > < (\cos \varphi +\sin \varphi )d\varphi \int\limits_0^1 < \left. x \right|_r^ < 2-r^2 >r^2dr > > =\pi \int\limits_0^1 < \left( < 4-5r^2+r^4 >\right)dr > =\frac < 38\pi > < 15 >. $ Применение сферических координат в этом примере нецелесообразно < громоздкое уравнение для параболоида >.

Решение:

Здесь область интегрирования — шар радиуса 1/2, сдвинутый по оси $\mathbf < \textit < Оz >> $ на 1/2 единицы, подынтегральная функция зависит от выражения $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >+\mathbf < \textit < z >> ^ < 2 >$, поэтому применим сферические координаты. Уравнение сферы $x^2+y^2+z^2=z\Rightarrow r^2=r\cos \theta \Rightarrow r=\cos \theta \left( < \Rightarrow 0\leqslant \theta \leqslant \pi /2 >\right)$ , поэтому $I=\iiint\limits_V < \sqrt < x^2+y^2+z^2 >dxdydz > =\iiint\limits_V < r\cdot r^2\sin \theta drd\varphi d\theta >=\int\limits_0^ < 2\pi > < d\varphi \int\limits_0^ < \pi /2 > < \sin \theta d\theta >\int\limits_0^ < \cos \theta > < r^3dr >> =\frac < 2\pi > < 4 >\int\limits_0^ < \pi /2 >< \left. < r^4 >\right|_0^ < \cos \theta >\sin \theta d\theta > = \\ =\frac < 2\pi > < 4 >\int\limits_0^ < \pi /2 > < \cos ^4\theta \sin \theta d\theta >=-\frac < 2\pi > < 4\cdot 5 >\left. < \cos ^5\theta >\right|_0^ < \pi /2 >=\frac < \pi > < 10 >$.

Вычислить объём тела, ограниченного поверхностью $\left( < x^2+y^2+z^2 >\right)^ < \,2 >=a^3z,\;a=const>0$

Решение:

Здесь тоже для того, чтобы понять, как устроено тело, и найти его объём, надо перейти к сферическим координатам < на это указывает комбинация $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >+\mathbf < \textit < z >> ^ < 2 >=\mathbf < \textit < r >> ^ < 2 >)$. Уравнение поверхности $\left( < x^2+y^2+z^2 >\right)^ < \,2 >=a^3z\Rightarrow r^4=a^3r\cos \vartheta \Rightarrow r=a\sqrt[3] < \cos \vartheta >\;\left( < \Rightarrow 0\leqslant \theta \leqslant \pi /2 >\right)$. По этому уравнению поверхность построить уже можно; отсутствие координаты $\varphi $ в уравнении показывает, что это — тело вращения вокруг оси $\mathbf < \textit < Oz >> $. Находим объём: $ V=\iiint\limits_V < r^2\sin \theta drd\varphi d\theta >=\int\limits_0^ < 2\pi > < d\varphi \int\limits_0^ < \pi /2 > < \sin >> \theta d\theta \int\limits_0^ < a\sqrt[3] < \cos \theta >> < r^2dr >=\frac < 2\pi > < 3 >\int\limits_0^ < \pi /2 >< \left. < r^3 >\right|_0^ < a\sqrt[3] < \cos \theta >> \sin \theta d\theta = > $ $ =\frac < 2\pi a^3 > < 3 >\int\limits_0^ < \pi /2 > < \cos \theta \sin \theta d\theta = >\frac < \pi a^3 > < 3 >. $

Вычислить интеграл $\iiint\limits_U < \left( < < x^4 >+ 2 < x^2 > < y^2 >+ < y^4 >>\right)dxdydz > ,$ где область (U) ограничена поверхностью ( < x^2 >+ < y^2 >\le 1) и плоскостями (z = 0,) (z = 1).

Решение:

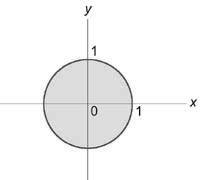
Данный интеграл удобно вычислить в цилиндрических координатах. Проекция области интегрирования на плоскость (Oxy) представляет собой круг ( < x^2 >+ < y^2 >\le 1) или (0 \le \rho \le 1).

Заметим, что подынтегральное выражение записывается в виде $ < \left( < < x^4 >+ 2 < x^2 > < y^2 >+ < y^4 >>\right) > = < < \left( < < x^2 >+ < y^2 >>\right)^2 > > = < < \left( < < \rho ^2 >>\right)^2 > = < \rho ^4 >> $

Тогда интеграл будет равен $I = \int\limits_0^ < 2\pi > < d\varphi >\int\limits_0^1 < < \rho ^4 >\rho d\rho > \int\limits_0^1 < dz >.$

Здесь во втором интеграле добавлен множитель (\rho) якобиан преобразования декартовых координат в цилиндрические. Все три интеграла по каждой из переменной не зависят друг от друга.

Вычислить интеграл $\iiint\limits_U < \left( < < x^2 >+ < y^2 >>\right)dxdydz > ,$ где область (U) ограничена поверхностями ( < x^2 >+ < y^2 >= 3z,) (z = 3)

Решение:

Область интегрирования изображена на рисунке

Для вычисления интеграла перейдем к цилиндрическим координатам: $ < x = \rho \cos \varphi , >\;\; < y = \rho \sin \varphi , >\;\; < z = z. >$ Дифференциал при этом равен $dxdydz = \rho d\rho d\varphi dz\;\;\left( < \rho - \text < якобиан >>\right).$

Уравнение параболической поверхности принимает вид: $ < \rho ^2 > < \cos ^2 >\varphi + < \rho ^2 > < \sin^2 >\varphi = 3z\;\;\text < или >\;\; < \rho ^2 >= 3z.$ Проекция области интегрирования (U) на плоскость (Oxy) представляет собой окружность ( < x^2 >+ < y^2 >\le 9) радиусом (\rho = 3).

Координата (\rho) изменяется в пределах от (0) до (3,) угол (\varphi) от (0) до (2\pi) и координата (z) от (\large\frac < < < \rho ^2 >> > < 3 >\normalsize) до (3.)

Используя цилиндрические координаты, найти значение интеграла $ I = \int\limits_ < - 2 >^2 < dx >\int\limits_ < - \sqrt < 4 - < x^2 >> > ^ < \sqrt < 4 - < x^2 >> > < dy >\int\limits_0^ < 4 - < x^2 >— < y^2 >> < < y^2 >dz > $

Решение:

Область интегрирования (U) изображена на рисунке:

Ее проекция на плоскость (Oxy) представляет собой круг ( < x^2 >+ < y^2 >= < 2^2 >):

Новые переменные в цилиндрических координатах будут изменяться в пределах $ < 0 \le \rho \le 2, >\;\; < 0 \le \varphi \le 2\pi , >\;\; < 0 \le z \le 4 - < \rho ^2 >. > $

Вычислить интеграл, используя цилиндрические координаты: $\iiint\limits_U < \sqrt < < x^2 >+ < y^2 >> dxdydz > .$ Область (U) ограничена параболоидом (z = 4 — < x^2 >— < y^2 >,) цилиндром ( < x^2 >+ < y^2 >= 4) и плоскостями (y = 0,) (z = 0)

Решение:

Изобразив схематически область интегрирования (U,) находим, что ее проекция на плоскость (Oxy) < область (D) >представляет собой полукруг радиусом (\rho = 2).

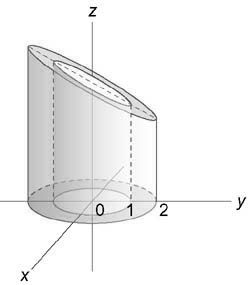
Найти интеграл $\iiint\limits_U < ydxdydz >,$ где область (U) ограничена плоскостями (z = x + 1,) (z = 0) и цилиндрическими поверхностями ( < x^2 >+ < y^2 >= 1,) ( < x^2 >+ < y^2 >= 4)

Решение:

Вычислим данный интеграл в цилиндрических координатах. Из условия $0 \le z \le x + 1$ следует, что $0 \le z \le \rho \cos \varphi + 1.$ Область интегрирования в плоскости (Oxy) представляет собой кольцо, ограниченное окружностями ( < x^2 >+ < y^2 >= 1) и ( < x^2 >+ < y^2 >= 4)

Следовательно, переменные (\rho) и (\varphi) изменяются в интервале $1 \le \rho \le 2,\;\;0 \le \varphi \le 2\pi .$

Этот результат закономерен, поскольку область (U) симметрична относительно плоскости (Oxz,) а подынтегральная функция является четной.

Найти интеграл (\iiint\limits_U < \sqrt < < x^2 >+ < y^2 >+ < z^2 >> dxdydz > ,) где область интегрирования (U) шар, заданный уравнением ( < < x^2 >+ < y^2 >+ < z^2 >> = 25.)

Решение:

Поскольку область (U) представляет собой шар, и к тому же подынтегральное выражение является функцией, зависящей от $f\left( < < x^2 >+ < y^2 >+ < z^2 >>\right),$ то перейдем к сферическим координатам.

Вычислить интеграл $\iiint\limits_U < < e^ < < < \left( < < x^2 >+ < y^2 >+ < z^2 >>\right) > ^ < \frac < 3 > < 2 >> > > > dxdydz > ,$ где область (U) представляет собой единичный шар ( < < x^2 >+ < y^2 >+ < z^2 >> \le 1.)

Решение:

Центр данного шара расположен в начале координат. Следовательно, в сферических координатах область интегрирования (U) описывается неравенствами $ < 0 \le \rho \le 1, >\;\; < 0 \le \varphi \le 2\pi , >\;\; < 0 \le \theta \le \pi . >$

Как видно, тройной интеграл вырождается в произведение трех однократных интегралов, каждый из которых вычисляется независимо. В результате находим $ < I = \int\limits_0^ < 2\pi > < d\varphi >\int\limits_0^1 < < e^ < < \rho ^3 >> > < \rho ^2 >d\rho > \int\limits_0^\pi < \sin \theta d\theta >> = < \left[ < \left. \varphi \right|_0^ < 2\pi >>\right] \cdot \int\limits_0^1 < \left( < < e^ < < \rho ^3 >> > \cdot \frac < 1 > < 3 >d < \rho ^3 >>\right) > \cdot \left[ < \left. < \left( < - \cos \theta >\right) >\right|_0^\pi >\right] > = < 2\pi \cdot \frac < 1 > < 3 >\left[ < \left. < \left( < < e^ < < \rho ^3 >> > >\right) >\right|_ < < \rho ^3 >= 0 > ^ < < \rho ^3 >= 1 > >\right] \cdot \left( < - \cos \pi + \cos 0 >\right) > = < \frac < < 2\pi >> < 3 >\cdot \left( < e - 1 >\right) \cdot 2 > = < \frac < < 4\pi >> < 3 >\left( < e - 1 >\right). > $

Вычислить интеграл (\iiint\limits_U < xyzdxdydz >,) где область (U) представляет собой часть шара ( < x^2 >+ < y^2 >+ < z^2 >\le < R^2 >,) расположенную в первом октанте (x \ge 0, y \ge 0, z \ge 0.)

Решение:

Найти тройной интеграл $\iiint\limits_U < \left( < \frac < < < x^2 >> > < < < a^2 >> > + \frac < < < y^2 >> > < < < b^2 >> > + \frac < < < z^2 >> > < < < c^2 >> > >\right)dxdydz > ,$ где область (U) ограничена эллипсоидом $ < \frac < < < x^2 >> > < < < a^2 >> > + \frac < < < y^2 >> > < < < b^2 >> > + \frac < < < z^2 >> > < < < c^2 >> > > = 1.$

Решение:

Для вычисления интеграла перейдем к обобщенным сферическим координатам путем следующей замены переменных: $ < x = a\rho \cos \varphi \sin \theta , >\;\; < y = b\rho \sin \varphi \sin \theta , >\;\; < z = c\rho \cos \theta . >$ Модуль якобиана данного преобразования равен (\left| I \right| = abc < \rho ^2 >\sin \theta .) Поэтому для дифференциалов справедливо соотношение $dxdydz = abc < \rho ^2 >\sin \theta d\rho d\varphi d\theta .$ В новых координатах интеграл принимает вид: $ < I = \iiint\limits_U < \left( < \frac < < < x^2 >> > < < < a^2 >> > + \frac < < < y^2 >> > < < < b^2 >> > + \frac < < < z^2 >> > < < < c^2 >> > >\right)dxdydz > > = < \iiint\limits_ < U' >< \left[ < \frac < < < < \left( < a\rho \cos \varphi \sin \theta >\right) > ^2 > > > < < < a^2 >> > + \frac < < < < \left( < b\rho \sin \varphi \sin \theta >\right) > ^2 > > > < < < b^2 >> > + \frac < < < < \left( < c\rho \cos \theta >\right) > ^2 > > > < < < c^2 >> > >\right]abc < \rho ^2 >\sin \theta d\rho d\varphi d\theta > > = \\ = < \iiint\limits_ < U' > < \left[ < < \rho ^2 > < < \cos >^2 > \varphi \, < < \sin >^2 > \theta + < \rho ^2 > < \sin^2 >\varphi \, < < \sin >^2 > \theta + < \rho ^2 > < < \cos >^2 > \theta >\right]abc < \rho ^2 >\sin \theta d\rho d\varphi d\theta > > = \\ = < \iiint\limits_ < U' > < \left[ < < \rho ^2 > < < \sin >^2 > \theta \underbrace < \left( < < < \cos >^2 > \varphi + < \sin^2 >\varphi >\right) > _1 + < \rho ^2 > < < \cos >^2 > \theta >\right]abc < \rho ^2 >\sin \theta d\rho d\varphi d\theta > > = \\ = < \iiint\limits_ < U' > < < \rho ^2 >\underbrace < \left( < < \sin^2 >\theta + < < \cos >^2 > \theta >\right) > _1abc < \rho ^2 >\sin \theta d\rho d\varphi d\theta > > = < abc\iiint\limits_ < U' > < < \rho ^4 >\sin \theta d\rho d\varphi d\theta > . > $

Вычислить интеграл $\int\limits_0^1 < dx >\int\limits_0^ < \sqrt < 1 - < x^2 >> > < dy >\int\limits_0^ < \sqrt < 1 - < x^2 >— < y^2 >> > < < < \left( < < x^2 >+ < y^2 >+ < z^2 >>\right) > ^2 > dz > ,$ используя сферические координаты.

Решение:

Область интегрирования представляет собой часть шара, расположенная в первом октанте и, следовательно, ограничена неравенствами $ < 0 \le \rho \le 1, >\;\; < 0 \le \varphi \le \frac < \pi > < 2 >, > \;\; < 0 \le \theta \le \frac < \pi > < 2 >. > $

Далее:

Формула Гаусса — Остроградского

Класс $S$. Теорема о замкнyтости класса $S$

Поток векторного поля через поверхность

Класс M. Теорема о замкнутости класса M

Несобственные интегралы по неограниченной области

Логические операции над высказываниями

Специальные векторные поля

Вычисление объёмов

Вычисление площади поверхности

Выражение площади плоской области через криволинейный интеграл

Вычисление криволинейного интеграла второго рода. Примеры.

Вычисление поверхностного интеграла первого рода

Теорема о предполных классах

Равносильные формулы алгебры высказываний

Огравление $\Rightarrow $

Уравнение параболоида в сферических координатах

Для функции трех переменных имеет место обобщение определенного интеграла — тройной интеграл (также кратный интеграл). Его теория аналогична теории двойного интеграла.

Пусть непрерывная функция u = f ( x , y , z ) задана в некоторой ограниченной замкнутой пространственной области V (рис. 6.4). Разобьем эту область на пространственные ячейки .

Тройным интегралом от функции f(M) по области V называется предел интегральной сумм ы при условии max d ( V_i ) → 0 , то есть при неограниченном увеличении числа ячеек, когда все ячейки стягиваются в точку:

Если такой предел существует, то функция f ( M ) называется интегрируемой в области V ; всякая непрерывная в ограниченной замкнутой области V функция f ( M ) интегрируема в ней. В дальнейшем мы будем рассматривать только непрерывные функции.

В декартовых координатах элемент объема обычно записывают в виде dν = dxdydz , а тройной интеграл обозначают

Тройной интеграл (6.9) выражает массу неоднородного тела объема V , с плотностью в каждой точке γ= f ( x , y , z ) посредством формулы:

Координаты центра тяжести тела вычисляются по формулам:

Если плотность γ=1, то тройной интеграл (6.9) будет выражать собой объем области V , а формулы (6.11) будут представлять координаты центра тяжести однородного тела.

1. Вычисление тройного интеграла в декартовой системе координат

Пусть V проектируется в область D на плоскости x 0 y так, что всякая прямая, параллельная оси 0 z и проходящая внутри области D , пересекает границу области V ровно в двух точках. В общем случае такая область ограничена сверху поверхностью z =ψ ₂ ( x , y ), снизу – поверхностью z =ψ ₁ ( x , y ) и с боков – цилиндрической поверхностью с образующими, параллельными оси 0 z (рис. 52). Такая область V называется правильной. В частных случаях боковая поверхность цилиндра может превратиться в линию. Функции ψ₁( x , y ) и ψ₂( x , y ) мы будем считать непрерывными. Тройной интеграл по такой области вычисляется по формуле

Здесь внутренний интеграл берется по z при фиксированных, но произвольных в D значениях x и y , от нижней границы области V до ее верхней границы , то есть по отрезку KL ( рис. 6.4). В результате получается некоторая функция двух переменных x и y , которая интегрируется затем по области D с помощью формул (6.5) или (6.6). Таким образом, вычисление тройного интеграла сводится к трехкратному интегрированию.

Наиболее простой вид формула (6.12) принимает в случае, когда V есть прямоугольный параллелепипед, ограниченный плоскостями :

Если область V имеет более сложную форму, то ее разбивают на конечное число областей , каждая из которых удовлетворяет условиям, изложенным выше.

Примечание . Аналогичные определения и формулы могут быть получены и тогда, когда область V проектируется в область D , лежащую или в плоскости x 0 z , или в плоскости y 0 z

Пример 6.4. Вычислить тройной интеграл , где область V ограничена координатными плоскостями и плоскостью x + y + z = 1 (рис. 6.5).

(единиц объема)

Пример 6.6. Найти массу тела ограниченного координатными плоскостями и плоскостью x + y + z = 1, если плотность в каждой его точке равна произведению координат этой точки, то есть γ = f ( x , y , z ) = x y z .

Решение . По условию область V совпадает с той областью, которая была рассмотрена в примере 6.4 (см. рис. 6.5). Искомая масса M согласно формуле (6.11) равна интегралу . Следовательно,

Чтобы вычислить полученный интеграл, положим 1– x = t ; тогда dx = – dt ; при этом t = 1 при x = 0 и t = 0 при x = 1.

Пример 6.7. Вычислить координаты центра тяжести куба , если плотность в каждой его точке равна произведению координат этой точки.

Решение . По условию плотность γ= x y z . Вычислим массу M куба по (6.10):

Из соображений симметрии следует x_c = y_c = z_c . Поэтому достаточно найти только одну координату x_c . Вычислим числитель для x_c в формуле (6.11).

2. Вычисление тройного интеграла в цилиндрических координатах

Для упрощения вычисления тройного интеграла часто бывает целесообразным перейти к цилиндрическим координатам. Точка M ( x ; y ; z ) в пространстве 0 xyz может быть определена заданием трех величин r ; φ ; z , где r – длина радиус-вектора проекции точки M на плоскость x 0 y , φ – угол, образованный этим радиус-вектором с осью 0 x , z – аппликата точки M (рис. 6.7). Эти числа ( r ; φ ; z ) называются цилиндрическими координатами точки M . Эти координаты связаны с ее декартовыми координатами соотношениями:

В этом случае тройной интеграл вычисляется по формуле

После применения (6.15) вычисление тройного интеграла сводится к трехкратному по r , по φ и по z согласно формуле (6.12).

Пример 6.8. Вычислить , где V – область, ограниченная частью конуса и плоскостью z = 2.

Решение . Заданная область V – часть конуса, вершина которого расположена в начале координат. Его уравнение в цилиндрических координатах (6.14) имеет вид

С учетом формулы замены (6.15) можем вычислить заданный тройной интеграл:

Обратим внимание на то, что, не переходя к цилиндрическим координатам, мы получили бы достаточно сложное трехкратное интегрирование согласно формуле (6.12)

Примечание. Переход к цилиндрическим координатам рационален, когда область интегрирования образована цилиндрической или конической поверхностью

3. Вычисление тройного интеграла в сферических координатах

Если область интегрирования V представляет собой шар или его часть (граница шара x 2 + y 2 + z 2 = R 2 в сферических координатах имеет очень простой вид ρ = R ), то удобно переходить к сферическим координатам.

Сферическими координатами точки M ( x ; y ; z ) пространства 0 xyz называется тройка чисел ρ ; φ; θ (рис. 6.8), где ρ – длина радиус-вектора точки M , φ – угол, образованный проекцией радиус-вектора на плоскость x 0 y и осью 0 x , θ – угол отклонения радиус-вектора от оси 0 z . Эти координаты связаны с декартовыми координатами точки M соотношениями:

В этом случае тройной интеграл вычисляется по формуле

Параболоиды: определение, виды, сечения

Определение параболоида

Эллиптическим параболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением

Гиперболическим параболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением

В уравнениях (4.51) и (4.52) и — положительные параметры, характеризующие параболоиды, причем для эллиптического параболоида .

Начало координат называют вершиной каждого из параболоидов ((4.50) или (4.51)).

Плоские сечения эллиптического параболоида

Плоскость пересекает эллиптический параболоид (4.51) по линии, имеющей в этой плоскости уравнение , которое равносильно уравнению параболы с фокальным параметром . Сечение параболоида плоскостью получаем, подставляя в уравнение (4.51): . Это уравнение равносильно уравнению параболы с фокальным параметром . Эти сечения называются главными параболами эллиптического параболоида (4.51).

Рассмотрим теперь сечение эллиптического параболоида плоскостями, параллельными плоскости . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.51), получаем

При уравнение не имеет действительных решений, т.е. плоскость при не пересекает параболоид (4.51). При уравнению (4.51) удовлетворяет одна вещественная точка — вершина параболоида. При 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> уравнение определяет эллипс с полуосями . Следовательно, сечение эллиптического параболоида плоскостью (при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» />) представляет собой эллипс, центр которого лежит на оси аппликат, а вершины — на главных параболах.

Таким образом, эллиптический параболоид можно представить как поверхность, образованную эллипсами, вершины которых лежат на главных параболах (рис.4.46,а).

Параболоид вращения

Эллиптический параболоид, у которого , называется параболоидом вращения . Такой параболоид является поверхностью вращения. Сечения параболоида вращения плоскостями (при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» />), представляют собой окружности с центрами на оси аппликат (рис.4.46,б). Его можно получить, вращая вокруг оси параболу , где .

Плоские сечения гиперболического параболоида

Сечения гиперболического параболоида координатными плоскостями и представляют собой параболы (главные параболы) или с параметрами или соответственно. Поскольку оси симметрии главных парабол направлены в противоположные стороны, гиперболический параболоид называют седловой поверхностью .

Рассмотрим теперь сечения гиперболического параболоида плоскостями, параллельными плоскости . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.52), получаем При 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> уравнение равносильно уравнению гиперболы полуосями , то есть сечение гиперболического параболоида плоскостью при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> представляет собой гиперболу с центром на оси аппликат, вершины которой лежат на главной параболе . При получаем уравнение сопряженной гиперболы с полуосями , т.е. сечение гиперболического параболоида плоскостью при представляет собой сопряженную гиперболу с центром на оси аппликат, вершины которой лежат на главной параболе . При получаем уравнение пересекающихся прямых , т.е. сечение гиперболического параболоида плоскостью представляет собой пару пересекающихся в начале координат прямых.

Таким образом, гиперболический параболоид можно представить как поверхность, образованную гиперболами (включая и «крест» из их асимптот), вершины которых лежат на главных параболах (рис.4.47,а).

Сечение параболоида плоскостью , где — произвольная постоянная, представляет собой параболу

равную главной параболе с параметром , вершина которой лежит на другой главной параболе с параметром . Поэтому гиперболический параболоид можно представить как поверхность, получающуюся при перемещении одной главной параболы так, чтобы ее вершина «скользила» по другой главной параболе (рис.4.47,б).

1. Гиперболический параболоид является линейчатой поверхностью, т.е. поверхностью, образованной движением прямой (рис.4.47,в).

2. Ось аппликат канонической системы координат является осью симметрии параболоида, а координатные плоскости — плоскостями симметрии параболоида.

В самом деле, если точка принадлежит параболоиду (эллиптическому или гиперболическому), то точки с координатами при любом выборе знаков также принадлежат параболоиду, поскольку их координаты удовлетворяют уравнению (4.51) или (4.52) соответственно. Поэтому параболоид симметричен относительно координатных плоскостей и координатной оси .