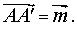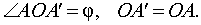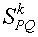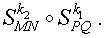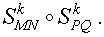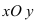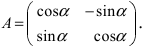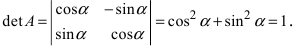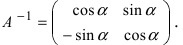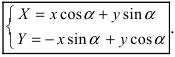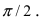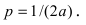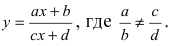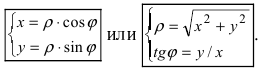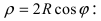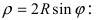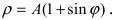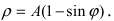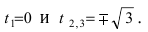Уравнение параллельного переноса на плоскости

Движения плоскости. Теорема Шаля.
Афинные преобразования плоскости

Преобразования плоскости

Движения плоскости

Теорема Шаля

Афинные преобразования плоскости

Классификация афинных преобразований плоскости

Преобразования плоскости

Определение 1 . Преобразованием плоскости называют правило, с помощью которого каждой точке плоскости ставится в соответствие точка этой же плоскости.

Из определения 1 вытекает, что, если F – преобразование плоскости α , а M – произвольная точка плоскости , то F(M) тоже является точкой плоскости α .

Определение 2 . Точку F(M) называют образом точки M при преобразовании F , а точку M называют прообразом точки F(M) при преобразовании F.

Аналогично определяются образы и прообразы любых фигур на плоскости при преобразовании F.

Определение 3 . Преобразование плоскости называют взаимно однозначным преобразованием плоскости на себя , если разные точки имеют разные образы, и каждая точка плоскости имеет прообраз.

Другими словами, при взаимно однозначном преобразовании плоскости на себя разные точки плоскости переходят в разные точки этой же плоскости, и в каждую точку плоскости переходит какая-то точка этой плоскости.

Определение 4 . Произведением (композицией) двух преобразований называют преобразование, которое получается в результате последовательного выполнения этих преобразований.

Таким образом, если F и G – два преобразования, то произведением этих преобразований будет такое преобразование H, которое произвольную точку A плоскости переводит в точку A’ этой плоскости, определяемую по формуле:

Движения плоскости

Определение 5 . Движением плоскости называют такое преобразование плоскости, при котором расстояние между двумя любыми точками плоскости равно расстоянию между их образами.

Следующие преобразования являются движениями плоскости:

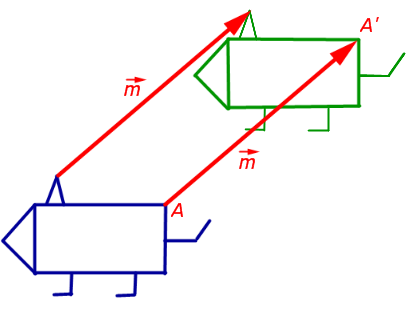
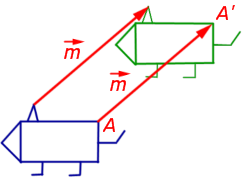
1. Параллельный перенос (сдвиг) на заданный вектор

При параллельном переносе плоскости на заданный вектор 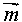(рис.1) произвольная точка A плоскости переходит в такую точку A’ плоскости, что выполнено равенство

Замечание . Движение, при котором каждая точка плоскости остаётся на своём месте, называют тождественным преобразованием . Тождественное преобразование можно рассматривать как параллельный перенос на вектор, равный нулю.

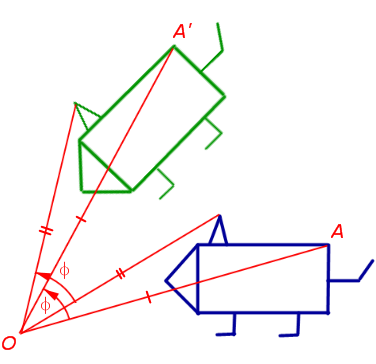
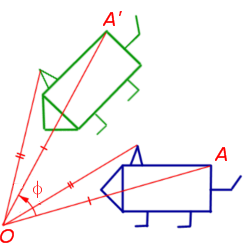
2. Поворот вокруг заданной точки, называемой центром поворота, на заданный угол

При повороте плоскости вокруг точки O на угол φ (рис. 2) произвольная точка A плоскости переходит в такую точку A’ плоскости, что выполнены равенства

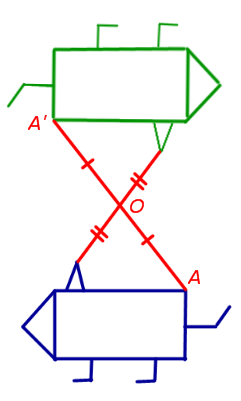
3. Центральная симметрия (симметрия относительно заданной точки, называемой центром симметрии)

При центральной симметрии плоскости относительно точки O произвольная точка A плоскости переходит в такую точку A’ плоскости, что серединой отрезка AA’ является точка O – заданный центр симметрии (рис.3).

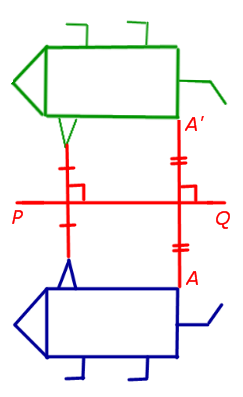
4. Осевая симметрия (симметрия относительно заданной прямой, называемой осью симметрии)

При осевой симметрии относительно прямой PQ ( ось симметрии ) произвольная точка A плоскости переходит в такую точку A’ плоскости, что, во-первых, прямая AA’ перпендикулярна прямой PQ , а, во-вторых, точка пересечения прямых AA’ и PQ является серединой отрезка AA’

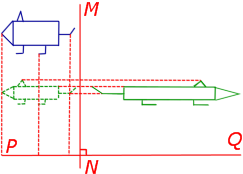
5. Скользящая симметрия (композиция осевой симметрии относительно заданной прямой и параллельного переноса на заданный отличный от нуля вектор, параллельный этой прямой)

Если прямая PQ – ось симметрии, а параллельный перенос задаётся вектором 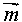параллельным прямой PQ , то результат скользящей симметрии можно условно изобразить так, как показано на рисунке 5.

Движения плоскости, сохраняющие ориентацию. Движения плоскости, изменяющие ориентацию. Теорема Шаля

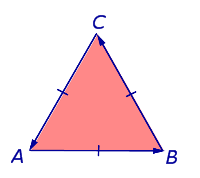
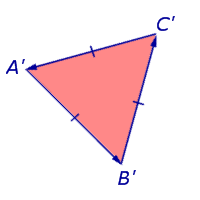
Рассмотрим на плоскости произвольный равносторонний треугольник и обозначим его вершины буквами A, B и C так, чтобы при обходе по сторонам треугольника в направлении

треугольник оказывался расположенным слева (рис.6). При таком обозначении вершин обход треугольника будет осуществляться против часовой стрелки.

Предположим теперь, что некоторое движение F переводит треугольник ABC в треугольник A’B’C’, у которого

Поскольку каждое движение плоскости сохраняет расстояния между точками, то треугольник A’B’C’ также будет равносторонним, однако возможны следующие два случая.

В первом случае при обходе по сторонам треугольника A’B’C’ в направлении

треугольник A’B’C’ располагается слева, и обход производится против часовой стрелки (рис.7).

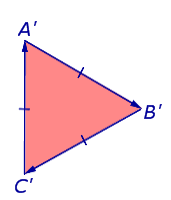
Во втором случае при обходе по сторонам треугольника A’B’C’ в направлении

треугольник A’B’C’ располагается справа, и обход производится по часовой стрелке (рис.8).

Определение 6 . Если при движении F осуществляется первый случай, то такое движение называют движением, сохраняющим ориентацию плоскости ( движением 1-го рода, собственным движением ). Если при движении F осуществляется второй случай, то такое движение называют движением, изменяющим ориентацию ( движением 2-го рода, несобственным движением ).

Классификацию всех движений плоскости даёт следующая теорема Шаля.

Теорема Шаля . Любое движение плоскости, сохраняющее ориентацию, является или параллельным переносом, или поворотом. Любое движение плоскости, изменяющее ориентацию, является или осевой симметрией, или скользящей симметрией.

Аффинные преобразования плоскости

Определение 7 . Аффинным преобразованием плоскости называют такое взаимно однозначное преобразование плоскости на себя, при котором образом любой прямой на плоскости является прямая.

Поскольку каждое движение плоскости переводит прямые линии в прямые линии, то каждое движение является аффинным преобразованием.

Однако аффинные преобразования не ограничиваются движениями плоскости. Следующие преобразования также являются аффинными преобразованиями плоскости:

1. Сжатие (растяжение) к прямой с заданным коэффициентом сжатия (растяжения)

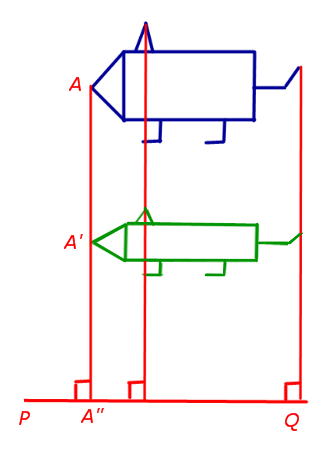
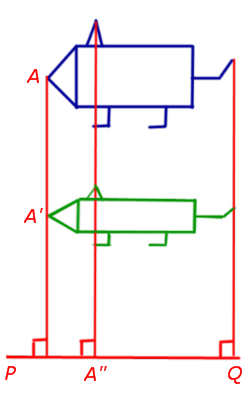
При сжатии (растяжении) плоскости к прямой PQ с заданным коэффициентом сжатия k (рис.9) произвольная точка A плоскости переходит в такую точку A’ плоскости, что выполнены следующие условия:

• прямая AA’ перпендикулярна прямой PQ ;
• если обозначить буквой A» точку пересечения прямых AA’ и PQ , то будет справедливо равенство

если k > 0 , то точки A и A’ лежат по одну сторону от прямой PQ , если же k , то точки A и A’ лежат по разные стороны от прямой PQ .

Замечание 1 . В случае, когда | k | , рассматриваемое аффинное преобразование называют сжатием к прямой PQ , если же | k | > 1 , то это преобразование называют растяжением .

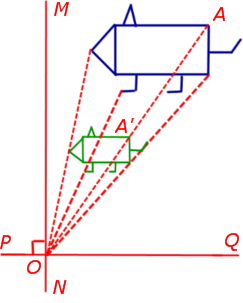
Замечание 2 . Будем использовать для рассматриваемого сжатия (растяжения) обозначение

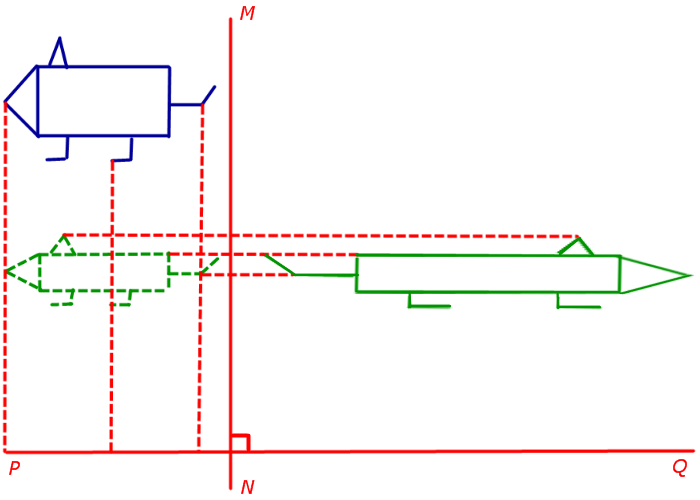
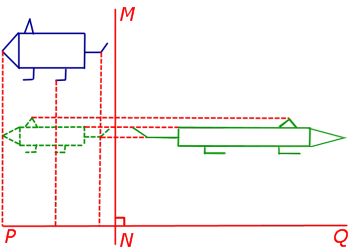
2. Сжатие (растяжение) по двум заданным взаимно перпендикулярным направлениям с заданными коэффициентами сжатия (растяжения)

Пусть PQ и MN – две взаимно перпендикулярных прямых, а числа k₁ и k₂ – коэффициенты сжатия (расширения) плоскости в направлении прямых PQ и MN соответственно. Тогда сжатием (растяжением) по двум заданным взаимно перпендикулярным направлениям PQ и MN с коэффициентами k₁ и k₂ (рис.10) называют композицию сжатий (растяжений).

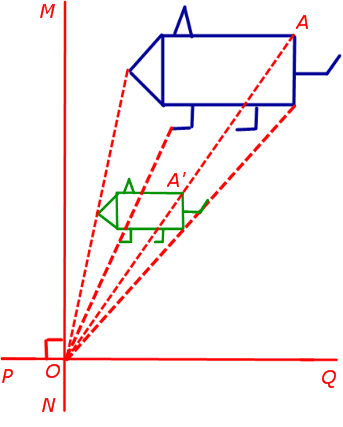
3. Гомотетия с заданным центром гомотетии и заданным коэффициентом сжатия (растяжения)

Гомотетией с центром в точке O и коэффициентом k называют такое аффинное преобразование, при котором произвольная точка A плоскости переходит в такую точку A’ плоскости, что выполнены следующие условия:

• точка A’ лежит на прямой AO ;
• справедливо равенство

если k > 0 , то точки A и A’ лежат по одну сторону от точки O , если же k , то точки A и A’ лежат по разные стороны от точки O (рис.11).

Замечание . Рассмотрим две произвольных взаимно перпендикулярных прямых PQ и MN, пересекающихся в точке O. Тогда гомотетия с центром в точке O и коэффициентом k совпадёт со сжатием (растяжением) по направлениям PQ и MN с коэффициентами, равными k . Другими словами, гомотетия является композицией сжатий (растяжений):

4. Преобразование подобия с заданным коэффициентом подобия

Преобразованием подобия с коэффициентом подобия k называют аффинное преобразование, представленное в виде композиции гомотетии с коэффициентом k и движения (рис. 12).

Классификация аффинных преобразований плоскости

Справедлива следующая теорема о классификации аффинных преобразований плоскости.

Преобразования декартовой системы координат с примерами решения

Содержание:

Преобразования декартовой системы координат

Параллельный перенос и поворот системы координат

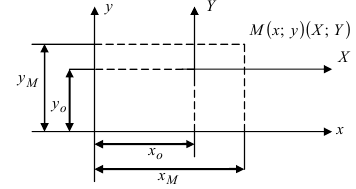
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):

Рис. 46. Параллельный перенос одной системы координат относительно другой системы.

Систему координат

Пример:

Дана точка М(3;2) и начало новой системы координат 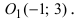Вычислить положение точки М в новой системе отсчета.

Решение:

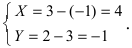
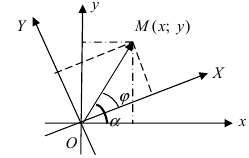
Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).

2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 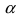(Рис. 47):

Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.

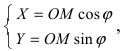
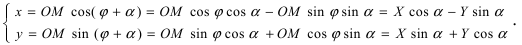
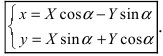
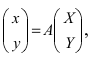
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода

Найдем обратное преобразование системы координат, найдем матрицу 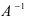обратную к матрице А:

Найдем алгебраические дополнения всех элементов

Запишем обратную матрицу

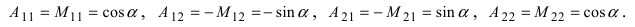
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.

Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.

Таким образом, имеем 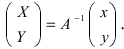Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:

Пример:

Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол

Решение:

Воспользуемся полученными формулами 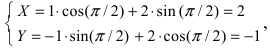т.е. в новой системе координат точка имеет координаты М(2; -1).

Рассмотрим применение преобразования координат:

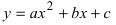
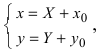
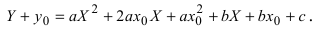
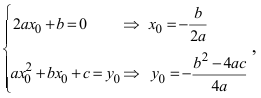
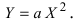
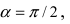
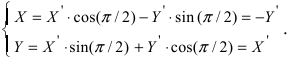
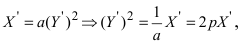
а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы

Пример:

Преобразовать уравнение параболы 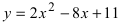к каноническому виду.

Решение:

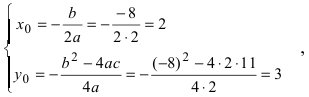
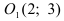
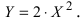
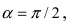
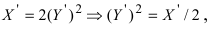
Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка — начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда

следовательно, параметр параболы р = 1/4.

б) Выяснить, какую кривую описывает функция

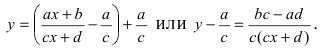
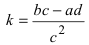
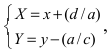
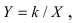
Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение

и новые координаты получим уравнение которое описывает равнобочную гиперболу.

Полярные координаты. Замечательные кривые

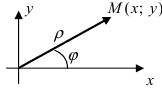
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 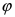между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).

Рис. 48. Полярная система координат.

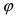
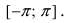
Главными значениями угла являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами

Рассмотрим замечательные кривые в полярной системе координат:

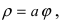
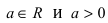
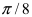
1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.

Рис. 49. Спираль (улитка) Архимеда.

2. Уравнение окружности: уравнение 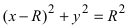описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид

Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.

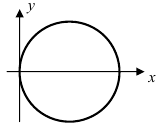
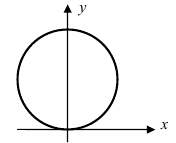
3. Уравнение 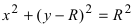описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид

Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.

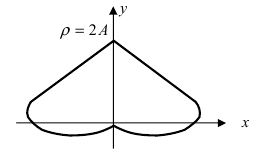
4. Кардиоиды:

Рис. 52. Кардиоида

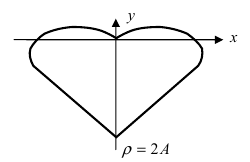
Рис. 53. Кардиоида

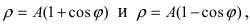
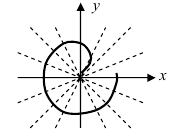
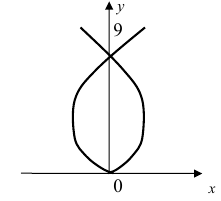
Аналогично выглядят кардиоиды но они вытянуты вдоль оси абсцисс Ох.

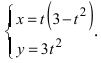
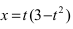
5. Петля: Величина равна нулю при

Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Бесконечно малые и бесконечно большие функции
• Замечательные пределы
• Непрерывность функций и точки разрыва
• Точки разрыва и их классификация
• Экстремум функции
• Методы решения систем линейных алгебраических уравнений (СЛАУ)
• Скалярное произведение и его свойства
• Векторное и смешанное произведения векторов

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Планиметрия. Страница 7

1 2 3 4 5 6 7 8 9 10 11 12

1.Движение и его свойства

Пусть на плоскости задана геометрическая фигура. Если каждую точку данной фигуры переместить на некоторое расстояние, так чтобы расстояние между точками сохранилось, то мы получим новую фигуру, преобразованную из данной. (Рис.1) Таким образом, преобразование одной фигуры в другую так, что расстояние между точками остается неизменным, называется движением.

Например, при перемещении фигуры М на некоторое расстояние получим фигуру М1. Все точки фигуры М передут в точки фигуры М1. Расстояние между точками сохранится АВ = А1В1

Свойства движения

При движение все точки, лежащие на прямой, перейдут в точки также лежащие на прямой. Порядок их взаимного расположения останется неизменным. Т.е. Прямые переходят в прямые, полупрямые — в полупрямые, отрезки — в отрезки и т.д. При движении градусная мера угла между двумя полупрямыми останется неизменной.

Рис.1 Движение и его свойства.

2.Симметрия относительно точки

Пусть на плоскости задана точка О. (Рис.2) Возьмем произвольную точку А. Если через точки О и А провести прямую и отложить от точки О отрезок ОА’, равный отрезку АО, то точка О будет называться точкой симметрии. А точка А’ — точкой симметричной точке А относительно точки О.

При преобразовании фигур каждая точка переходит в симметричную ей точку относительно точки симметрии О. Такое преобразование называется преобразованием симметрии, а фигуры называются симметричными относительно точки О.

Если при преобразовании фигура переходит в саму себя, то она называется центрально-симметричной, а точка О называется точкой симметрии. Например, параллелограмм, окружность, эллипс, ромб, квадрат.

Преобразование фигур относительно точки симметрии является движением.

Рис.2 Симметрия относительно точки.

3.Симметрия относительно прямой

Пусть дана прямая а. (Рис.3). Если взять произвольную точку, например точку Е, провести перпендикуляр к прямой а и на продолжении этого перпендикуляра отложить отрезок ВE’, равный отрезку ЕВ, то точка Е’ будет симметрична относительно прямой а. Если точка лежит на прямой а, то она симметрична сама себе.

При преобразовании фигуры в фигуру каждая точка переходит в точку С’, симметричную относительно прямой а. Такое преобразование называется преобразование симметрии относительно прямой.

Преобразование симметрии относительно прямой также является движением, т.к. согласно определению движения расстояние между точками фигуры при смещении относительно прямой не изменяется.

Рис.3 Симметрия относительно прямой.

4.Параллельный перенос и его свойства

Пусть на плоскости с осями координат Ox и Oy задана фигура S. Каждая точка фигуры параллельным переносом переходит в точку А’ на одно и тоже расстояние. Тогда можно дать следующее определение: преобразование фигуры S в фигуру S’, в котором каждая точка фигуры с координатами x и y смещается в точку с координатами x+a и y+b, где a и b постоянные числа, называется параллельным переносом.

Параллельный перенос есть движение, т.к. все точки смещаются на одно и тоже расстояние.

Таким образом, для получения координат новой фигуры, параллельный перенос задается следующими формулами:

x’ = x + a
y’ = y + b

Свойства параллельного переноса

При параллельном переносе все точки какой-либо фигуры смещаются по параллельным прямым на одно и тоже расстояние. Перпендикулярные прямые переходят в перпендикулярные прямые, параллельные прямые — в параллельные. Расстояния между точками какой-либо фигуры при перемещении, так же как и углы между прямыми, сохраняются.

Рис.4 Параллельный перенос и его свойства.

Репетитор: Васильев Алексей Александрович

Предметы: математика, физика, информатика, экономика, программирование.

2000 руб / 120 мин — подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин — индивидуально (базовый уровень). 2000 руб / 120 мин — студенты.

Тел. 8 916 461-50-69, email: alexey-it@ya.ru

5.Пример 1

Докажите, что у параллелограмма точка пересечения диагоналей является центром симметрии.

Доказательство:

Пусть дан параллелограмм АВA’В’ (Рис.5). По свойству параллелограмма, его диагонали делятся точкой пересечения пополам, а противолежащие стороны параллельны и равны. Следовательно, треугольники АОB’ и ВОА’ равны по двум сторонам и углу между ними. АО = ОА’, ВО = ОB’, углы при вершине О равны как вертикальные. А отсюда следует, что точки A’ и B’ симметричны точкам А и В относительно точки О. Т.е. получается, что вершины параллелограмма центрально симметричны относительно точки О.

Теперь на стороне АВ’ возьмем произвольную точку Е и проведем через нее прямую, проходящую через точку О. Треугольники ЕОВ’ и BOE’ равны по второму признаку равенства треугольников: по стороне и прилегающим к ней углам. BO = OB’ и углы при вершинах О и В,B’ равны (при вершине О как вертикальные, при вершинах B,B’ как внутренние накрест лежащие). Следовательно, отрезки ЕО и ОE’ равны, т.е. ЕО = ОE’.

Рис.5 Задача. Докажите, что у параллелограмма.

Отсюда можно сделать вывод, что каждая точка Х параллелограмма переходит в точку X’, симметричную относительно данной точки О. Т.е. преобразование симметрии относительно точки О переводит параллелограмм в сам себя, поэтому он называется центрально-симметричной фигурой, а точка О является его центром симметрии.

Пример 2

Докажите, что прямая, содержащая медиану равнобедренного треугольника, которая проведена к основанию, является его осью симметрии.

Доказательство:

Пусть АВА’ данный равнобедренный треугольник с основанием АА’, АВ = ВA’ (Рис.6). Медиана ОВ лежит на прямой а. Так как медиана делит противолежащую сторону пополам, то треугольники АВО и A’BO равны по трем сторонам (АВ = ВA’, АО = ОA’, сторона ОВ у них общая). Следовательно, углы при вершине О равны 90°, как равные смежные углы. А углы при вершине В равны, так как треугольники равны. Следовательно, вершина треугольника А симметрична вершине A’ относительно прямой а, так как основание АA’ перпендикулярно прямой а. Так же как и для любой точки, принадлежащей отрезку АО, найдется симметричная ей точка на отрезке ОА’ относительно прямой а.

Точка В лежит на прямой а, поэтому она симметрична сама себе относительно прямой а.

Теперь проведем произвольную прямую b, параллельную основанию АА’. Она пересечет боковые стороны треугольника в точках ЕЕ’. Рассмотрим треугольники ЕВО’ и BO’E’. Они равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам: сторона BO’ у них общая, углы при вершинах В и О’ равны). Следовательно, ЕО’ = O’E’.

Рис.6 Задача. Докажите, что прямая, содержащая медиану.

Отсюда следует, что любая точка Х’ треугольника ВОА’ симметрична точке Х треугольника АВО относительно прямой а, что является преобразованием симметрии относительно прямой. А если преобразование симметрии относительно прямой а переводит треугольник АВА’ сам в себя, то прямая а является его осью симметрии.

Пример 3

Параллельный перенос задается формулами x’ = x + 2, y’ = y — 3. В какие точки при этом параллельном переносе переходят точки А (1;1), В (2;2), С (-2;0).

Решение:

По условию задачи параллельный перенос задается формулами:

x’ = x + 2, y’ = y — 3

Следовательно, точка А переходит в точку А’ с координатами:

x’ = 1 + 2 = 3, y’ = 1 — 3 = -2, т.е. A’ (3;-2).

Точка В переходит в точку В’ с координатами:

x’ = 2 + 2 = 4, y’ = 2 — 3 = -1, т.е. В’ (4;-1).

Точка С переходит в точку С’ с координатами:

x’ = -2 + 2 = 0, y’ = 0 — 3 = -3, т.е. С’ (0;-3). (Рис.7)

Рис.7 Задача. Параллельный перенос задается формулами.

Пример 4

Докажите, что если у двух ромбов равны диагонали, то они равны.

Доказательство:

Пусть даны два ромба: ABCD и A»B»С»D». AC = A»C», BD = B»D». Углы между диагоналями равны 90°. Докажем, что они совмещаются движением, причем вершина А переходит в вершину A», вершина В — в B», вершина С — в С», вершина D — в D».

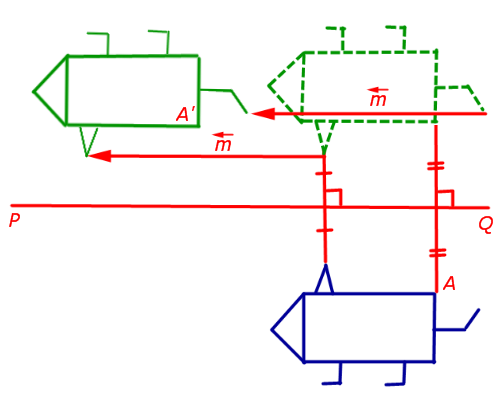
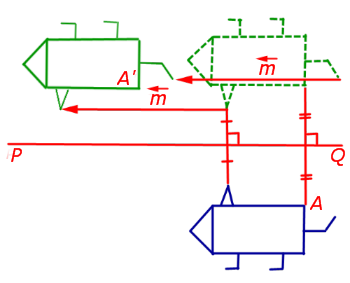
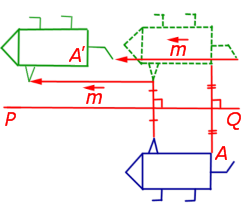
Подвергнем ромб ABCD преобразованию симметрии относительно прямой а, перпендикулярной отрезку СС’ и проходящей через его середину (Рис.8). Если два ромба не располагаются друг под другом, то нужного расположения можно добиться при помощи параллельного переноса. (Напомним, что параллельный перенос также является движением со всеми вытекающими из этого свойствами.) В результате получим ромб A’B’C’D’. Если точки А и А’ различны, то подвергнем его симметрии относительно прямой b, перпндикулярной отрезку A’A» и проходящей через его середину и точку С’. Таким образом, отрезок A’C’ перейдет в отрезок A»C». И в результате получим ромб A»B»’C»D»’.

Преобразование симметрии относительно прямой является движением. А при движении точки переходят в точки, прямые — в прямые, углы между прямыми, так же как и расстояния между точками, сохраняются.

Рис.8 Задача. Докажите, что если у двух ромбов.

Отсюда следует, что отрезок B»’D»’ перпендикулярен отрезку А»C» и проходит через его середину, а точки B»’ и D»’ совпадают с точками B» и D», так как по условию задачи диагонали двух ромбов равны. Таким образом, получается, что диагонали ромба АС и BD полностью совпадут с диагоналями A»C» и B»D». А из этого следует, что и вершины ромба ABCD полностью совпадут с вершинами ромба A»B»C»D», так как они находятся на концах диагоналей. Следовательно, ромб ABCD полностью перейдет в ромб A»B»C»D».

Пример 5

Существует ли параллельный перенос, при котором точка А (2;2) переходит в точку A'(3;-2), а точка В (-2;1) переходит в точку В'(-2;-3).

Решение:

Параллельный перенос задается формулами:

x’ = x + a, y’ = y + b

где а и b одни и те же числа. Отсюда следует, что

a = x’ — x, b = y’ — y. Подставим координаты точки А и A’:

a = 3 — 2, b = -2 — 2; т.е. a = 1, b = -4

Следовательно, параллельный перенос по точке А задается формулами: x’ = x + 1, y’ = y — 4

Отсюда, координаты точки В» будут:

x» = -2 + 1 = -1, y» = 1 — 4 = -3

т.е. B»(-1;-3), а точка B’ имеет координаты (-2;-3).

Следовательно, такого параллельного переноса не существует. (Рис.9)

Рис.9 Задача. Существует ли параллельный перенос.