I Классификация кривых второго порядка
Читайте также:
|
 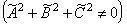 | (1) |
Одна и та же кривая в зависимости от расположения, относительно ДПСК будет, иметь разные уравнения. Оказывается, что для каждой кривой, определяемой уравнением (1), можно подобрать такую новую ДПСК ( повернутую), что ее уравнение примет вид:
| Ax 2 + By 2 + Cx + Dy + E = 0; (A 2 + B 2 ≠ 0), | (2) |
т.е. уравнение не будет содержать произведение xy.
В типовом расчете дается именно это уравнение (2), поэтому мы и будем его рассматривать.
Вид кривой, определяемой уравнением (2), зависит от коэффициентов A, B, C, D, E поэтому проведем подробный анализ каждого из следующих случаев.
1. AB ≠ 0, т.е. A ≠ 0 и B ≠ 0 случай центральной кривой.
Выделим полные квадраты:


Таким образом (2) примет вид
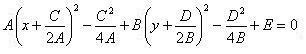 | (3) |
Положим α = –C / 2A, β = –D / 2B и 
тогда получим
| A(x – α) 2 + B(y – β) 2 = H | (4) |
Перейдем теперь к новой ДПСК – X′O′Y′, которая получается из исходной ДПСК XOY параллельным переносом (соответствующие оси координат параллельны и сонаправлены). Начало ДПСК X′O′Y′ поместим в т. O′(α, β ). Тогда точка M, имеющая относительно ДПСК XOY координаты (Х,У) будет иметь относительно ДПСК X′O′Y′ координаты x’ = x – α и y’ = y – β, а уравнение (4) в ДПСК X′O′Y′ запишется
 | (5) |
(для удобства в дальнейшем вместо x’ и y’ будем писать x и y).
1.1 AB > 0 – эллиптический тип.
a) A > 0, B > 0, H > 0.
Положив 

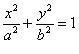 | (6) |
В этом уравнении, не нарушая общности, можно считать a 2 ≥ b 2 , в противном случае нужно просто ДПСК повернуть на 90°.
Кривая, уравнение которой относительно некоторой ДПСК имеет вид 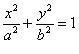
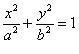
b) A > 0, B > 0, H = 0.
Положив a 2 = 1 / A, b 2 = 1 / B, получим

Этому уравнению удовлетворяют координаты единственной точки O’ (0,0).
c) A > 0, B > 0, H 2 = – H / A, b 2 = – H / B, перепишем (5) в виде: 
Полученному уравнению не удовлетворяют координаты ни одной точки, т.е. оно определяет пустое множество точек. Условно это пустое множество называют мнимым эллипсом.
Таким образом мы полностью проанализировали ситуацию, когда AB > 0. Теперь перейдем к следующему случаю.
1.2 AB 0, B 0.
Положив a 2 = H / A, b 2 = –H / B, перепишем (5) в виде
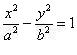 | (7) |
Кривая, уравнение которой относительно некоторой ДПСК имеет вид 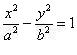
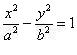
Замечание. Если A > 0, B 0, то (5) можно преобразовать к виду 

b) A > 0, B 2 = 1 / A, b 2 = –1 / B, получим: 
Разложим левую часть на множители: 
Теперь хорошо видно, что этому уравнению удовлетворяют координаты точек двух прямых, проходящих через начало координат O’ (0,0): 


2 AB = 0 – параболический тип.
2.1 A = 0 (B ≠ 0), C ≠ 0. В этом случае (2) имеет вид:
By 2 + Cx + Dy + E = 0.
Выделив полный квадрат, преобразуем это уравнение:
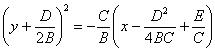
Положим, далее, 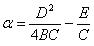

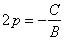
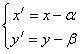
получим: (y’ ) 2 = 2px’. Опустим для удобства штрихи:
| y 2 = 2px | (8) |
Кривая, уравнение которой относительно некоторой ДПСК имеет вид y 2 = 2px, называется параболой. Уравнение y 2 = 2px называется каноническим уравнением параболы.
Замечание. В уравнении (8), не нарушая общности, можно считать p > 0, в противном случае нужно повернуть ДПСК на 180°.
Замечание. Случай B = 0, D ≠ 0, очевидно, сводится к предыдущему, если повернуть ДПСК на 90°.
Наконец, чтобы полностью завершить анализ уравнения (7.2) нам осталось рассмотреть последние три случая.
2.2 A = 0 (B ≠ 0), C = 0.
В этом случае уравнение (2) имеет вид By 2 + Dy + E = 0.
Выделив полный квадрат, преобразуем его к виду: 
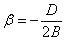


| y 2 = H | (9) |
a) H > 0
Обозначим a 2 = H тогда (9) примет вид:
| y 2 = a 2 | (10) |
Этому уравнению удовлетворяют координаты точек, лежащих на параллельных прямых y = a и y = –a (вырожденная парабола).
b) H 2 = –H, перепишем (9) в виде: y 2 = –a 2 . Этому уравнению не удовлетворяют координаты ни одной точки, т.е. оно определяет пустое множество, которое условно называют парой мнимых параллельных прямых.
c) H = 0
То есть (9) имеет вид
| y 2 = 0 | (11) |
Этому уравнению удовлетворяют координаты точек оси абсцисс. Так как уравнение (11) есть “предельный” случай (10) (a 2 → 0), то говорят, что уравнению y 2 = 0 соответствует пара совпадающих параллельных прямых.
Замечание. Случай B = 0 и D = 0 сводится к предыдущему поворотом осей на 90°.
Таким образом, подобрав новую ДПСК, уравнение Ax 2 + By 2 + Cx + Dy + E = 0 можно привести к одному из следующих 9 видов (см. таблицу).
| Классификация алгебраических кривых второго порядка | |||
| Номер вида | Уравнение кривой | Название кривой | Рисунок кривой |
| Эллиптический тип кривой (AB > 0) | |||
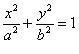 (a > b > 0) (a > b > 0) | Эллипс |  | |
 | Точка |  | |
 | Мнимый эллипс |  | |
| Гиперболический тип кривой (AB 2 = 2px (p > 0) | Парабола |  | |
| y 2 = b 2 | Пара параллельных прямых (вырожденная парабола) |  | |
| y 2 = –b 2 | Пара мнимых паралельных прямых |  | |
| y 2 = 0 | Пара совпадающих параллельных прямых |  | |
| Уравнения 1-5 относятся к случаю центральной кривой, так как каждое из них описывает либо пустое множество, либо множество, имеющее единственный центр |
Наш анализ показывает, что из всех алгебраических кривых второго порядка интерес представляют только эллипс, гипербола и парабола (прямые мы рассматривали ранее). Эти кривые действительно обладают рядом замечательных свойств, которые используются в технике. Отметим важнейшие из них.
| II ЭЛЛИПС | 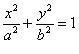 (a > b > 0) (a > b > 0) |
1. Эллипс имеет центр симметрии – начало координат O(0,0).
2. Эллипс имеет две оси симметрии – оси координат.
3. Точки пересечения эллипса с осями симметрии называются вершинами – A1(–a,c), A2(a,0), B1(0,–b), B2(0,b) (4 вершины).
4. Отрезок A1A2 называется большой осью эллипса, длина этой оси равна 2a; аналогично, отрезок B1 B2 называется малой осью эллипса, длина малой оси 2b (2b 2c).
6. Эксцентриситетом эллипса называется число ε = c/a.
Заметим, что эксцентриситет эллипса ε 0, b > 0)
1. Гипербола имеет центр симметрии – начало координат т.O(0,0).
2. Гипербола имеет две оси симметрии – оси координат.
3. Точки пересечения с осями симметрии называются вершинами гиперболы. В отличие от эллипса гипербола имеет 2 вершины: A1(–a, 0) и A2(a, 0) – т.е. гипербола пересекает только одну ось симметрии.
4. Отрезок A1A2 называется действительной осью гиперболы, длина действительной оси равна 2a. Точки B1(0, –b) и B2(0, b) лежат на оси симметрии, которую гипербола не пересекает. Отрезок B1B2 называется мнимой осью гиперболы, длина мнимой оси равна 2b .
Все сказанное далее в предыдущем разделе II п.4 для эллипса, касающееся полуосей и терминологии, относится и к гиперболе.
5. Точки, лежащие на продолжении действительной оси гиперболы F1(–C, 0) и F2(C, 0), где 
Фокальное свойство гиперболы: для любой точки M, лежащей на гиперболе ||F1M| – |F2M|| = 2a, т.е. гипербола является множеством точек плоскости, для которых модуль разности расстояний до двух данных точек плоскости, фокусов, есть величина постоянная, равная 2a > 0.
6. Эксцентриситетом гиперболы называется число ε = C/a.
Заметим, что эксцентриситет гиперболы ε > 1.
7. Прямые z1: x = – a/ε и z2: x = a/ε перпендикулярные действительной оси гиперболы, называются директрисами.
Директориальное свойство гиперболы дословно формулируется так же, как и для эллипса, только ε 2 = 2px(p > 0)
1. Парабола в отличие от эллипса и гиперболы, не имеет центра симметрии, т.е. не относится к центральным кривым.
2. Парабола имеет одну ось симметрии – ось абсцисс.
3. Точка пересечения параболы с осью симметрии называется вершиной – т. О(0,0), т.е. парабола имеет одну вершину.
4. Число p > 0 называется параметром параболы.
5. Точка 
6. Прямая 
Директориальное свойство параболы: для любой точки M, лежащей на параболе, |FM| = ρ(M,L), т.е. |FM| / ρM(L) = 1 и можно считать, что эксцентриситет параболы ε = 1. Таким образом, парабола занимает промежуточное положение между эллипсом, у которого ε 1.
Замечание. Директориальное свойство является определяющим для параболы так же , как и для эллипса, и для гиперболы.
7. Оптическое свойство параболы: луч, идущий из фокуса, отразившись от параболы, идет параллельно оси параболы, т.е. параболическое зеркало дает параллельный пучок света, если источник поместить в фокус параболы.
На рис. 7.3 изображена парабола с ее замечательными точками и прямыми.

Рис. 7.3 Парабола
Замечание. Форма параболы хорошо известна из школьного курса, так как парабола является графиком квадратного трехчлена.
Содержание типового расчета
Четыре алгебраические кривые второго порядка заданы уравнениями вида
Ax 2 + By 2 + Cx + Dy + E = 0.
Определить тип каждой кривой, найти ее основные параметры и сделать чертеж.
Дата добавления: 2015-04-15 ; просмотров: 20 ; Нарушение авторских прав
Теоремы, связанные с кривыми второго порядка
Содержание
1.Кривые второго порядка
2.Теоремы, связанные с кривыми второго порядка
Введение
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.
Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.
Кривые второго порядка
Кривой 2-го порядка называется линия на плоскости, которая в некоторой декартовой системе координат определяется уравнением
ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0
где a, b, c, d, e, f — вещественные коэффициенты, причем a2 + b2 + c2 ≠ 0 .
Вид кривой зависит от четырёх инвариантов:
инварианты относительно поворота и сдвига системы координат:
инвариант относительно поворота системы координат (полуинвариант):
Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой:
Так, например, невырожденная кривая 

Корни этого уравнения являются собственными значениями вещественной симметричной матрицы и, как следствие этого, всегда вещественны:
Кривые второго порядка классифицируются на невырожденные кривые и вырожденные.
Доказано, что кривая 2–го порядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс, гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих), точка, пустое множество.
Иными словами, для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид:
Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющие точку эллипса с фокусами, называются фокальными радиусами точки.
Если эллипс описывается каноническим уравнением
где a > 0 , b > 0, a > b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметрично на оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где
Величина e = c/a называется эксцентриситетом эллипса.
По определению эллипса r1 + r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам
Если фокусы эллипса совпадают, то эллипс является окружностью.
Гипербола
Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
где a > 0, b > 0 — параметры гиперболы.
Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.
В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.
Точки пересечения гиперболы с осью OX ( ± a, 0) называются вершинами гиперболы.
С осью OY гипербола не пересекается.
Отрезки a и b называются полуосями гиперболы.
Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.
Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b).
Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.
Парабола
Параболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
где p > 0 — параметр параболы.
Такое уравнение называется каноническим уравнением параболы, а система координат, в которой парабола описывается каноническим уравнением, называется канонической.
В канонической системе ось абсцисс является осью симметрии параболы, а начало координат — её вершиной.
Уравнения y2 = −2 px, x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координат также описывают параболы:
Теоремы, связанные с кривыми второго порядка
Теоремма Паскамля — теорема проективной геометрии, которая гласит, что:
Если шестиугольник вписан в окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу, даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат на одной прямой. Теорема Паскаля двойственна к теореме Брианшона.
Теорема Брианшона является классической теоремой проективной геометрии. Она сформулируется следующим образом:
Если шестиугольник описан около конического сечения, то три диагонали, соединяющие противоположные вершины этого шестиугольника, проходят через одну точку.
В частности, в вырожденном случае:
Если стороны шестиугольника проходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположные вершины, проходят через одну точку.
Теорема Брианшона двойственна к теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.
Литература
1. Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.
2. Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.
3. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия, гл. 6. М.: «Наука», 1988.
Уравнение пары параллельных прямых является вырожденным случаем параболы
I Классификация кривых второго порядка
Читайте также:
|
Исследование кривых второго порядка
Цель работы
Определить вид кривых, найти их основные характеристики и сделать рисунки.
Теоретическое введение
I Классификация кривых второго порядка
Алгебраической кривой второго порядка называется кривая, уравнение которой в декартовой прямоугольной системе координат (ДПСК) можно представить в виде:
 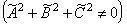 | (1) |
Одна и та же кривая в зависимости от расположения, относительно ДПСК будет, иметь разные уравнения. Оказывается, что для каждой кривой, определяемой уравнением (1), можно подобрать такую новую ДПСК ( повернутую), что ее уравнение примет вид:
| Ax 2 + By 2 + Cx + Dy + E = 0; (A 2 + B 2 ≠ 0), | (2) |
т.е. уравнение не будет содержать произведение xy.
В типовом расчете дается именно это уравнение (2), поэтому мы и будем его рассматривать.
Вид кривой, определяемой уравнением (2), зависит от коэффициентов A, B, C, D, E поэтому проведем подробный анализ каждого из следующих случаев.
1. AB ≠ 0, т.е. A ≠ 0 и B ≠ 0 случай центральной кривой.
Выделим полные квадраты:

Таким образом (2) примет вид
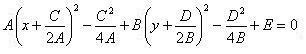 | (3) |
Положим α = –C / 2A, β = –D / 2B и
тогда получим
| A(x – α) 2 + B(y – β) 2 = H | (4) |
Перейдем теперь к новой ДПСК – X′O′Y′, которая получается из исходной ДПСК XOY параллельным переносом (соответствующие оси координат параллельны и сонаправлены). Начало ДПСК X′O′Y′ поместим в т. O′(α, β ). Тогда точка M, имеющая относительно ДПСК XOY координаты (Х,У) будет иметь относительно ДПСК X′O′Y′ координаты x’ = x – α и y’ = y – β, а уравнение (4) в ДПСК X′O′Y′ запишется
 | (5) |
(для удобства в дальнейшем вместо x’ и y’ будем писать x и y).
1.1 AB > 0 – эллиптический тип.
a) A > 0, B > 0, H > 0.
Положив 
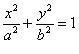 | (6) |
В этом уравнении, не нарушая общности, можно считать a 2 ≥ b 2 , в противном случае нужно просто ДПСК повернуть на 90°.
Кривая, уравнение которой относительно некоторой ДПСК имеет вид 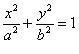
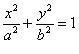
b) A > 0, B > 0, H = 0.
Положив a 2 = 1 / A, b 2 = 1 / B, получим 
Этому уравнению удовлетворяют координаты единственной точки O’ (0,0).
c) A > 0, B > 0, H 2 = – H / A, b 2 = – H / B, перепишем (5) в виде: 
Полученному уравнению не удовлетворяют координаты ни одной точки, т.е. оно определяет пустое множество точек. Условно это пустое множество называют мнимым эллипсом.
Таким образом мы полностью проанализировали ситуацию, когда AB > 0. Теперь перейдем к следующему случаю.
1.2 AB 0, B 0.
Положив a 2 = H / A, b 2 = –H / B, перепишем (5) в виде
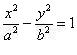 | (7) |
Кривая, уравнение которой относительно некоторой ДПСК имеет вид 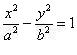
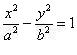
Замечание. Если A > 0, B 0, то (5) можно преобразовать к виду 

b) A > 0, B 2 = 1 / A, b 2 = –1 / B, получим: 
Разложим левую часть на множители: 
Теперь хорошо видно, что этому уравнению удовлетворяют координаты точек двух прямых, проходящих через начало координат O’ (0,0): 


2 AB = 0 – параболический тип.
2.1 A = 0 (B ≠ 0), C ≠ 0. В этом случае (2) имеет вид:
By 2 + Cx + Dy + E = 0.
Выделив полный квадрат, преобразуем это уравнение: 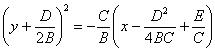
Положим, далее, 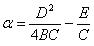

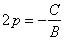
получим: (y’ ) 2 = 2px’. Опустим для удобства штрихи:
| y 2 = 2px | (8) |
Кривая, уравнение которой относительно некоторой ДПСК имеет вид y 2 = 2px, называется параболой. Уравнение y 2 = 2px называется каноническим уравнением параболы.
Замечание. В уравнении (8), не нарушая общности, можно считать p > 0, в противном случае нужно повернуть ДПСК на 180°.
Замечание. Случай B = 0, D ≠ 0, очевидно, сводится к предыдущему, если повернуть ДПСК на 90°.
Наконец, чтобы полностью завершить анализ уравнения (7.2) нам осталось рассмотреть последние три случая.
2.2 A = 0 (B ≠ 0), C = 0.
В этом случае уравнение (2) имеет вид By 2 + Dy + E = 0.
Выделив полный квадрат, преобразуем его к виду: 
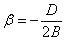


| y 2 = H | (9) |
a) H > 0
Обозначим a 2 = H тогда (9) примет вид:
| y 2 = a 2 | (10) |
Этому уравнению удовлетворяют координаты точек, лежащих на параллельных прямых y = a и y = –a (вырожденная парабола).
b) H 2 = –H, перепишем (9) в виде: y 2 = –a 2 . Этому уравнению не удовлетворяют координаты ни одной точки, т.е. оно определяет пустое множество, которое условно называют парой мнимых параллельных прямых.
c) H = 0
То есть (9) имеет вид
| y 2 = 0 | (11) |
Этому уравнению удовлетворяют координаты точек оси абсцисс. Так как уравнение (11) есть “предельный” случай (10) (a 2 → 0), то говорят, что уравнению y 2 = 0 соответствует пара совпадающих параллельных прямых.
Замечание. Случай B = 0 и D = 0 сводится к предыдущему поворотом осей на 90°.
Таким образом, подобрав новую ДПСК, уравнение Ax 2 + By 2 + Cx + Dy + E = 0 можно привести к одному из следующих 9 видов (см. таблицу).
| Классификация алгебраических кривых второго порядка | |||
| Номер вида | Уравнение кривой | Название кривой | Рисунок кривой |
| Эллиптический тип кривой (AB > 0) | |||
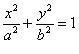 (a > b > 0) (a > b > 0) | Эллипс |  | |
 | Точка |  | |
 | Мнимый эллипс |  | |
| Гиперболический тип кривой (AB 2 = 2px (p > 0) | Парабола |  | |
| y 2 = b 2 | Пара параллельных прямых (вырожденная парабола) |  | |
| y 2 = –b 2 | Пара мнимых паралельных прямых |  | |
| y 2 = 0 | Пара совпадающих параллельных прямых |  | |
| Уравнения 1-5 относятся к случаю центральной кривой, так как каждое из них описывает либо пустое множество, либо множество, имеющее единственный центр |
Наш анализ показывает, что из всех алгебраических кривых второго порядка интерес представляют только эллипс, гипербола и парабола (прямые мы рассматривали ранее). Эти кривые действительно обладают рядом замечательных свойств, которые используются в технике. Отметим важнейшие из них.
| II ЭЛЛИПС | 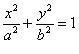 (a > b > 0) (a > b > 0) |
1. Эллипс имеет центр симметрии – начало координат O(0,0).
2. Эллипс имеет две оси симметрии – оси координат.
3. Точки пересечения эллипса с осями симметрии называются вершинами – A1(–a,c), A2(a,0), B1(0,–b), B2(0,b) (4 вершины).
4. Отрезок A1A2 называется большой осью эллипса, длина этой оси равна 2a; аналогично, отрезок B1 B2 называется малой осью эллипса, длина малой оси 2b (2b 2c).
6. Эксцентриситетом эллипса называется число ε = c/a.
Заметим, что эксцентриситет эллипса ε 0, b > 0)
1. Гипербола имеет центр симметрии – начало координат т.O(0,0).
2. Гипербола имеет две оси симметрии – оси координат.
3. Точки пересечения с осями симметрии называются вершинами гиперболы. В отличие от эллипса гипербола имеет 2 вершины: A1(–a, 0) и A2(a, 0) – т.е. гипербола пересекает только одну ось симметрии.
4. Отрезок A1A2 называется действительной осью гиперболы, длина действительной оси равна 2a. Точки B1(0, –b) и B2(0, b) лежат на оси симметрии, которую гипербола не пересекает. Отрезок B1B2 называется мнимой осью гиперболы, длина мнимой оси равна 2b .
Все сказанное далее в предыдущем разделе II п.4 для эллипса, касающееся полуосей и терминологии, относится и к гиперболе.
5. Точки, лежащие на продолжении действительной оси гиперболы F1(–C, 0) и F2(C, 0), где 
Фокальное свойство гиперболы: для любой точки M, лежащей на гиперболе ||F1M| – |F2M|| = 2a, т.е. гипербола является множеством точек плоскости, для которых модуль разности расстояний до двух данных точек плоскости, фокусов, есть величина постоянная, равная 2a > 0.
6. Эксцентриситетом гиперболы называется число ε = C/a.
Заметим, что эксцентриситет гиперболы ε > 1.
7. Прямые z1: x = – a/ε и z2: x = a/ε перпендикулярные действительной оси гиперболы, называются директрисами.
Директориальное свойство гиперболы дословно формулируется так же, как и для эллипса, только ε 2 = 2px(p > 0)
1. Парабола в отличие от эллипса и гиперболы, не имеет центра симметрии, т.е. не относится к центральным кривым.
2. Парабола имеет одну ось симметрии – ось абсцисс.
3. Точка пересечения параболы с осью симметрии называется вершиной – т. О(0,0), т.е. парабола имеет одну вершину.
4. Число p > 0 называется параметром параболы.
5. Точка 
6. Прямая 
Директориальное свойство параболы: для любой точки M, лежащей на параболе, |FM| = ρ(M,L), т.е. |FM| / ρM(L) = 1 и можно считать, что эксцентриситет параболы ε = 1. Таким образом, парабола занимает промежуточное положение между эллипсом, у которого ε 1.
Замечание. Директориальное свойство является определяющим для параболы так же , как и для эллипса, и для гиперболы.
7. Оптическое свойство параболы: луч, идущий из фокуса, отразившись от параболы, идет параллельно оси параболы, т.е. параболическое зеркало дает параллельный пучок света, если источник поместить в фокус параболы.
На рис. 7.3 изображена парабола с ее замечательными точками и прямыми.
Рис. 7.3 Парабола
Замечание. Форма параболы хорошо известна из школьного курса, так как парабола является графиком квадратного трехчлена.
Содержание типового расчета
Четыре алгебраические кривые второго порядка заданы уравнениями вида
Ax 2 + By 2 + Cx + Dy + E = 0.
Определить тип каждой кривой, найти ее основные параметры и сделать чертеж.
Дата добавления: 2015-04-15 ; просмотров: 20 ; Нарушение авторских прав
Классификация кривых второго порядка.
Кривые второго порядка представлены вырожденными и невырожденными кривыми.
Вырожденные кривые второго порядка это такие прямые и точки, которые определяются уравнением второго порядка. Когда уравнению второй степени не соответствует ни одна точка плоскости, то для их обозначения указывают, что уравнение демонстрирует вырожденную кривую (мнимую кривую второго порядка).
Следовательно, образцами вырожденных кривых второго порядка будут:
— точка;
Когда кривая невырожденная, то для неё имеется декартова (прямоугольная) система координат в которой уравнение исследуемой кривой примет единственный из трёх возможных вариантов:
х 2 / b 2 — у 2 / b 2 =1 – каноническое уравнение гиперболы;
у 2 = 2pх — каноническое уравнение параболы.
Теоремы, связанные с кривыми второго порядка
Содержание
1.Кривые второго порядка
2.Теоремы, связанные с кривыми второго порядка
Введение
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.
Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.
Кривые второго порядка
Кривой 2-го порядка называется линия на плоскости, которая в некоторой декартовой системе координат определяется уравнением
ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0
где a, b, c, d, e, f — вещественные коэффициенты, причем a2 + b2 + c2 ≠ 0 .
Вид кривой зависит от четырёх инвариантов:
инварианты относительно поворота и сдвига системы координат:
инвариант относительно поворота системы координат (полуинвариант):
Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой:
Так, например, невырожденная кривая 

Корни этого уравнения являются собственными значениями вещественной симметричной матрицы и, как следствие этого, всегда вещественны:
Кривые второго порядка классифицируются на невырожденные кривые и вырожденные.
Доказано, что кривая 2–го порядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс, гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих), точка, пустое множество.
Иными словами, для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид:
Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющие точку эллипса с фокусами, называются фокальными радиусами точки.
Если эллипс описывается каноническим уравнением
где a > 0 , b > 0, a > b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметрично на оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где
Величина e = c/a называется эксцентриситетом эллипса.
По определению эллипса r1 + r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам
Если фокусы эллипса совпадают, то эллипс является окружностью.
Гипербола
Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
где a > 0, b > 0 — параметры гиперболы.
Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.
В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.
Точки пересечения гиперболы с осью OX ( ± a, 0) называются вершинами гиперболы.
С осью OY гипербола не пересекается.
Отрезки a и b называются полуосями гиперболы.
Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.
Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b).
Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.
Парабола
Параболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
где p > 0 — параметр параболы.
Такое уравнение называется каноническим уравнением параболы, а система координат, в которой парабола описывается каноническим уравнением, называется канонической.
В канонической системе ось абсцисс является осью симметрии параболы, а начало координат — её вершиной.
Уравнения y2 = −2 px, x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координат также описывают параболы:
Теоремы, связанные с кривыми второго порядка
Теоремма Паскамля — теорема проективной геометрии, которая гласит, что:
Если шестиугольник вписан в окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу, даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат на одной прямой. Теорема Паскаля двойственна к теореме Брианшона.
Теорема Брианшона является классической теоремой проективной геометрии. Она сформулируется следующим образом:
Если шестиугольник описан около конического сечения, то три диагонали, соединяющие противоположные вершины этого шестиугольника, проходят через одну точку.
В частности, в вырожденном случае:
Если стороны шестиугольника проходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположные вершины, проходят через одну точку.
Теорема Брианшона двойственна к теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.
Литература
1. Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.
2. Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.
3. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия, гл. 6. М.: «Наука», 1988.
http://poisk-ru.ru/s41174t17.html
http://b4.cooksy.ru/articles/uravnenie-pary-parallelnyh-pryamyh-yavlyaetsya-vyrozhdennym-sluchaem-paraboly


















