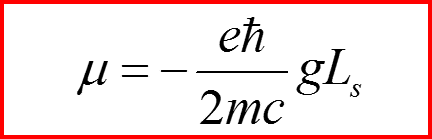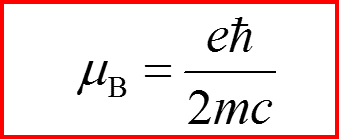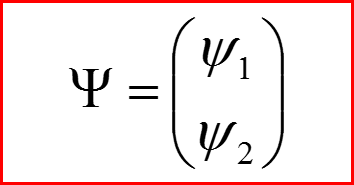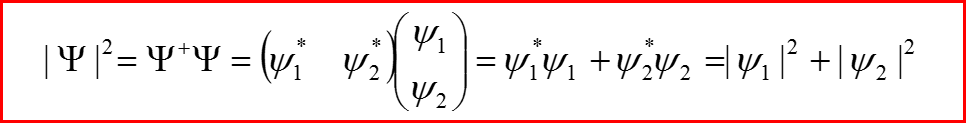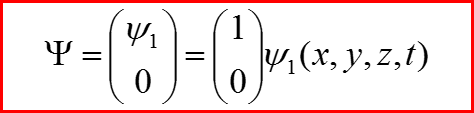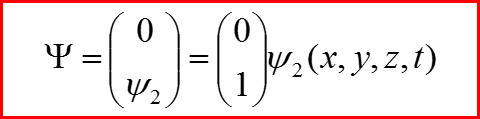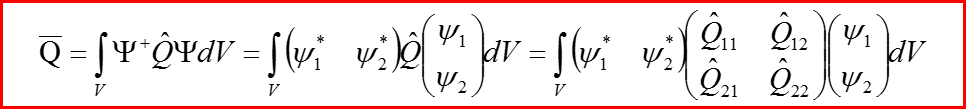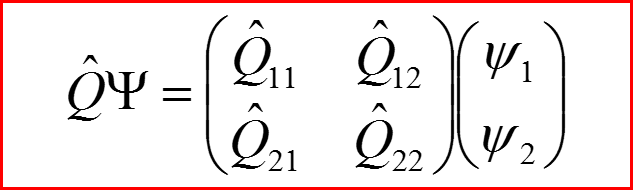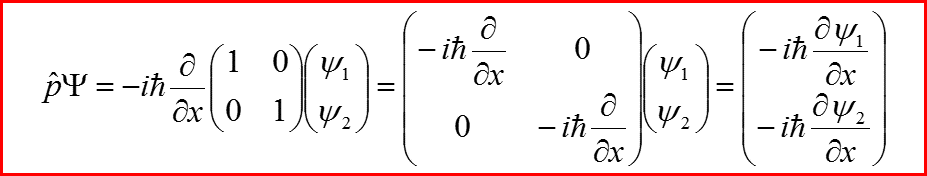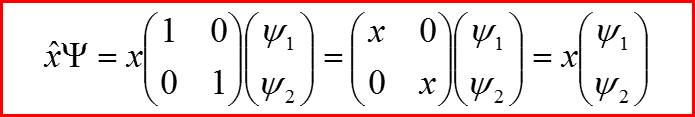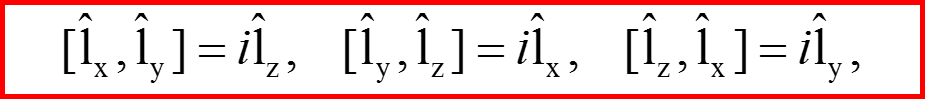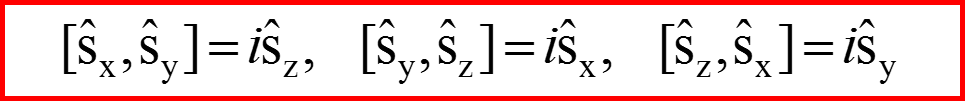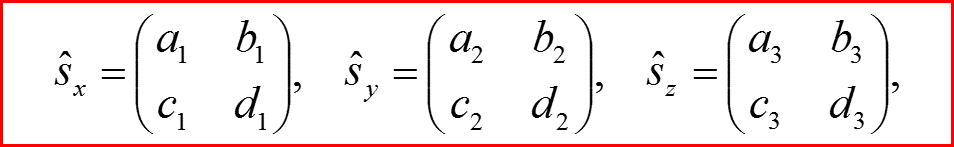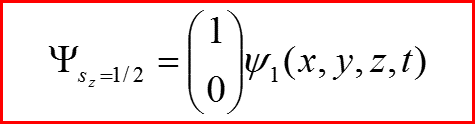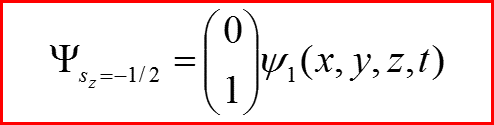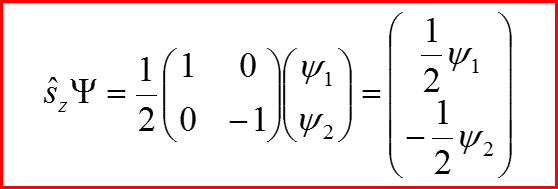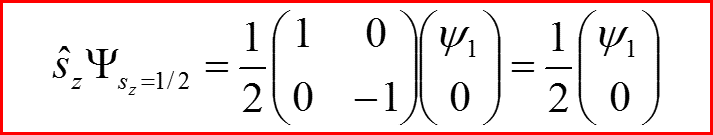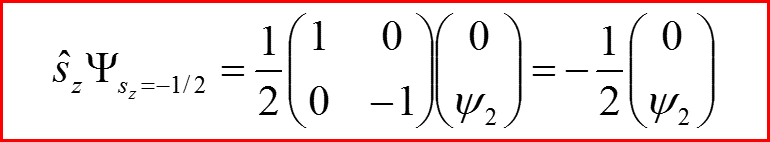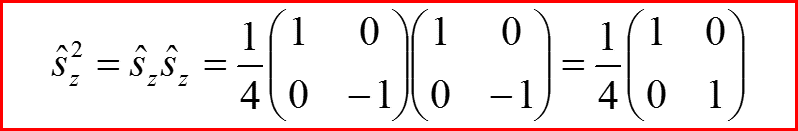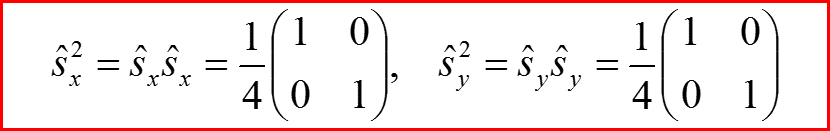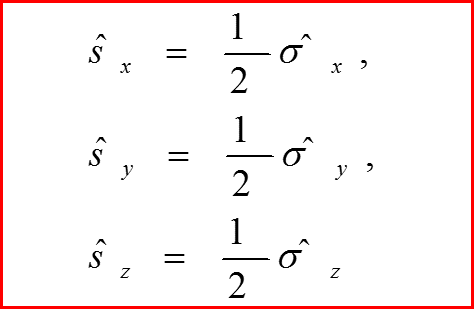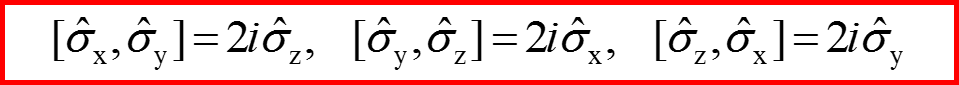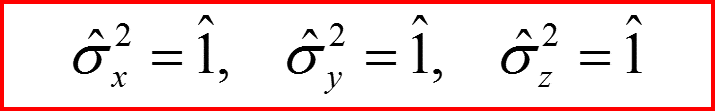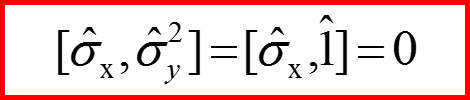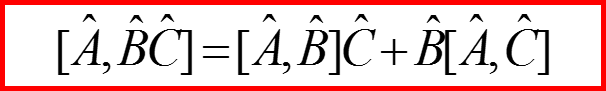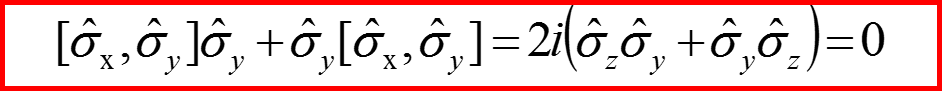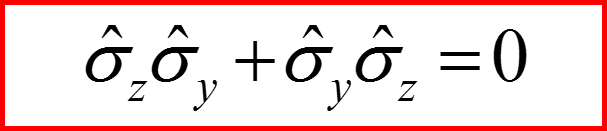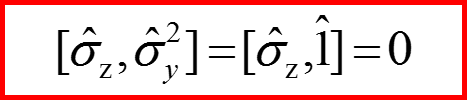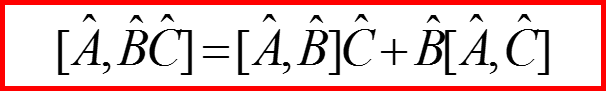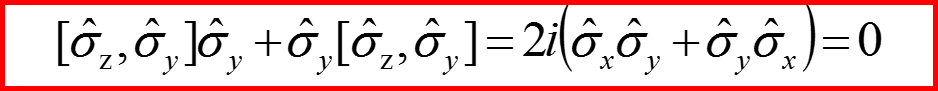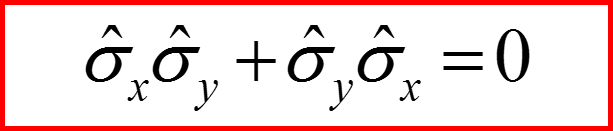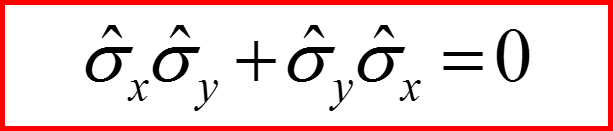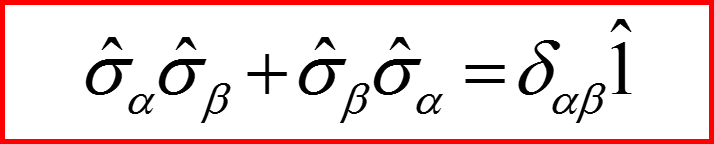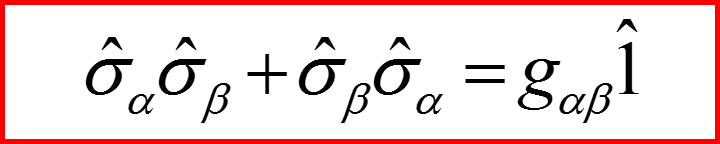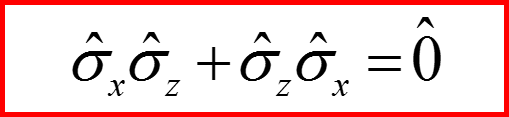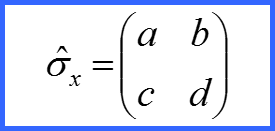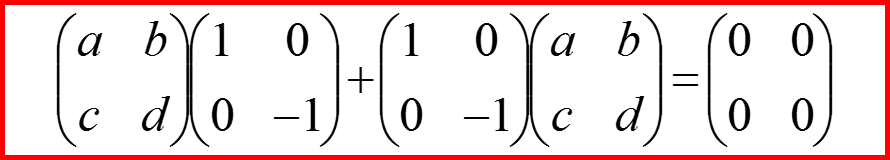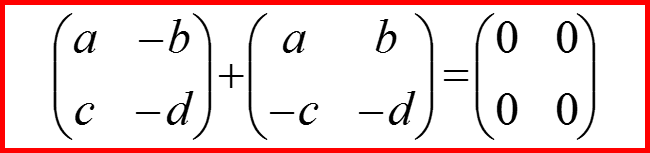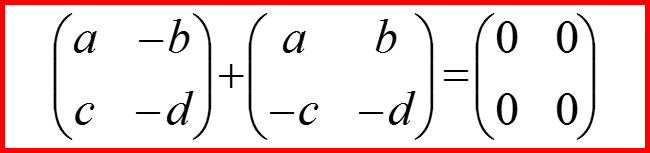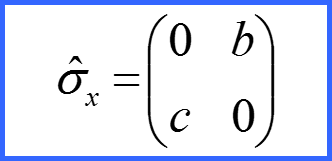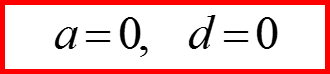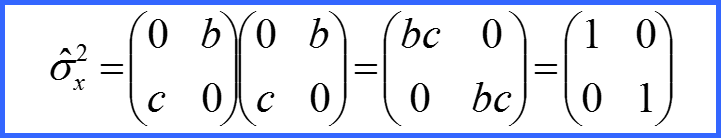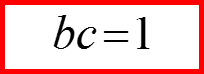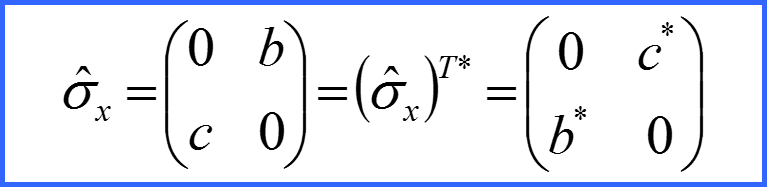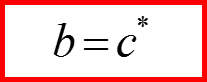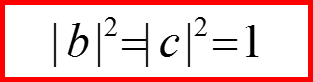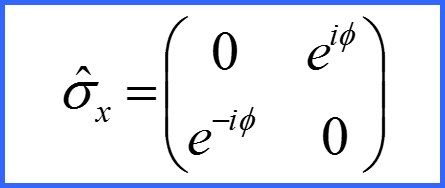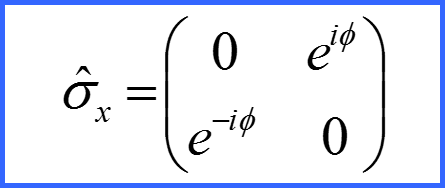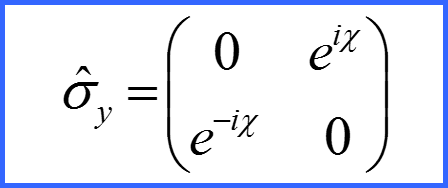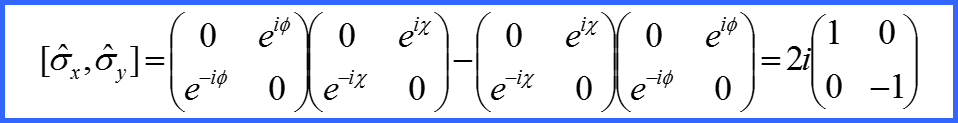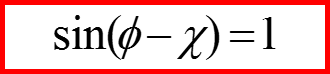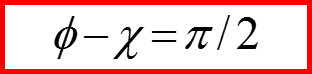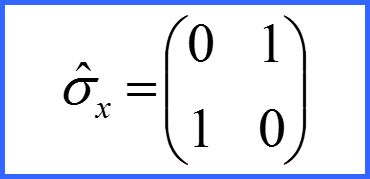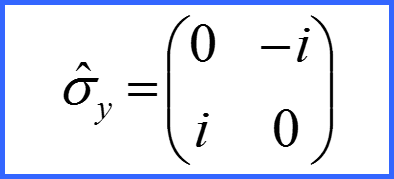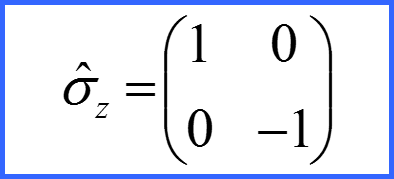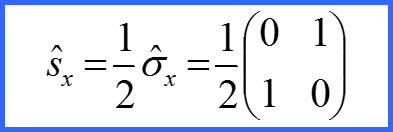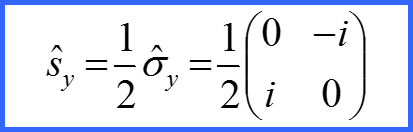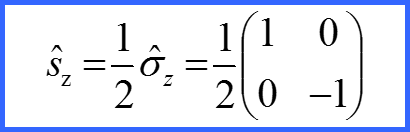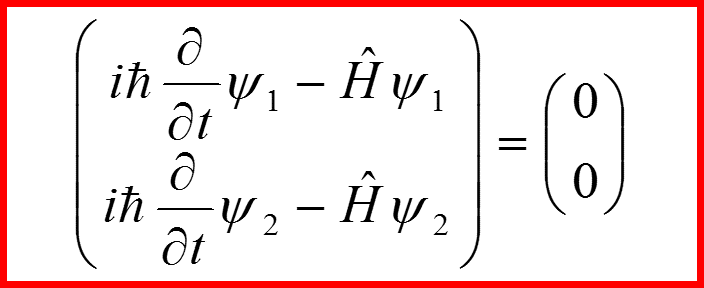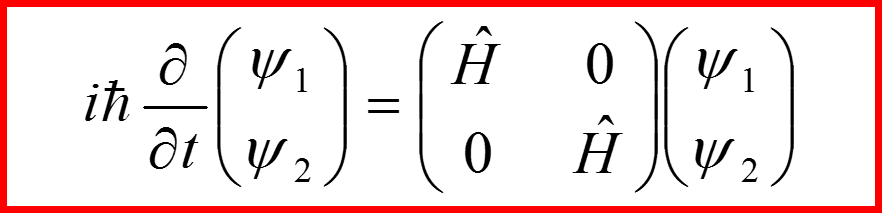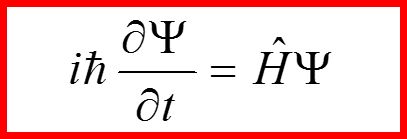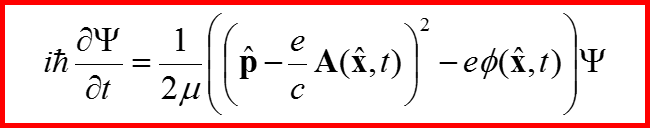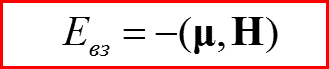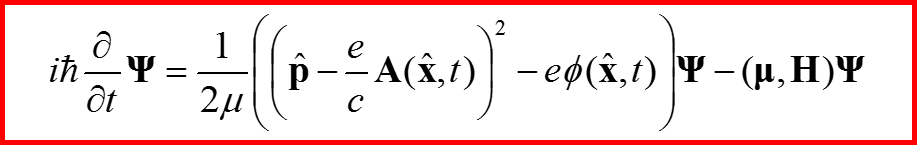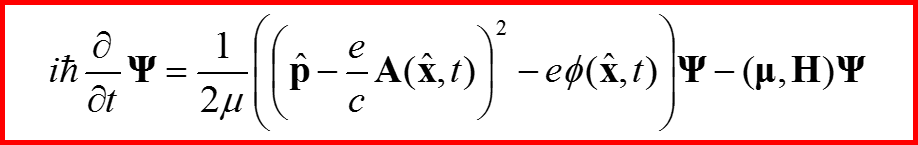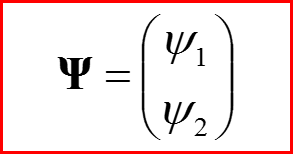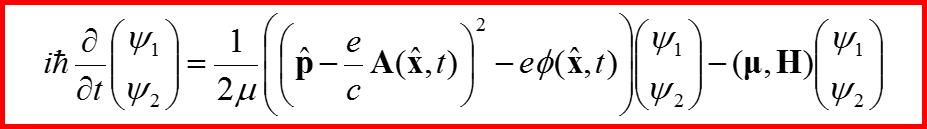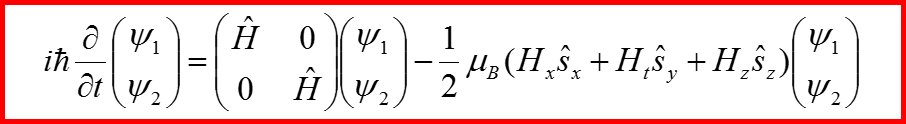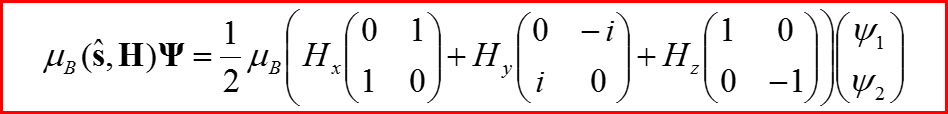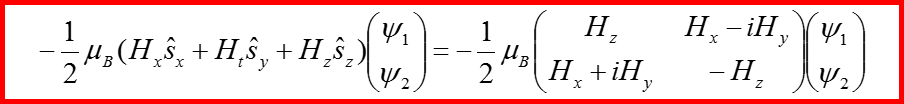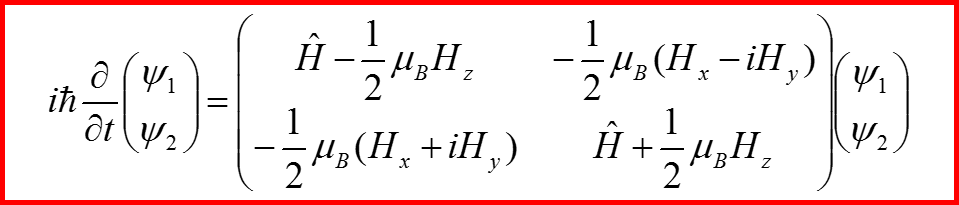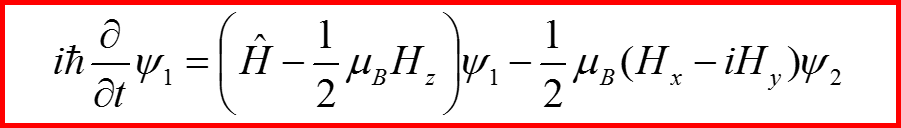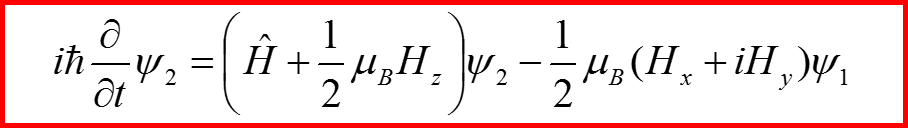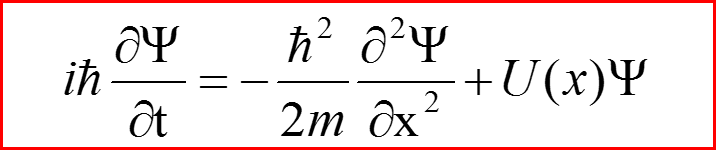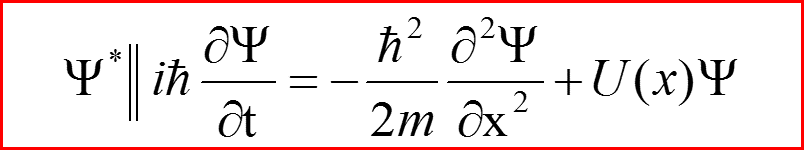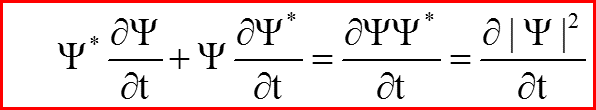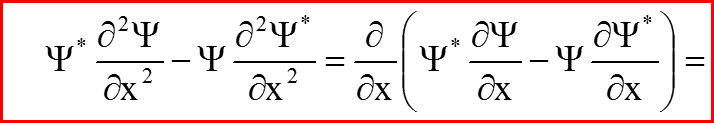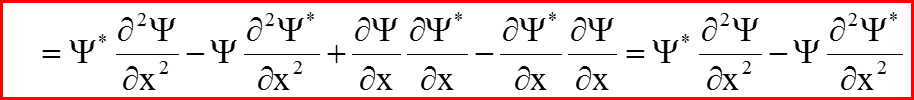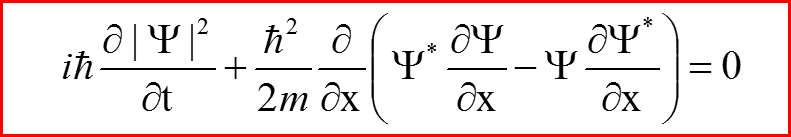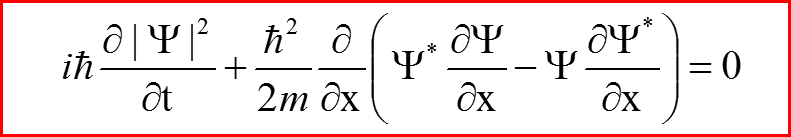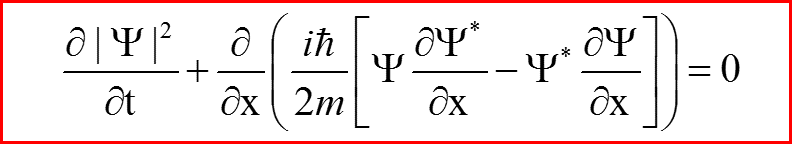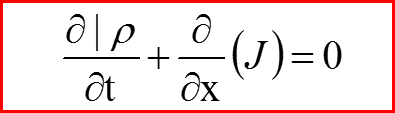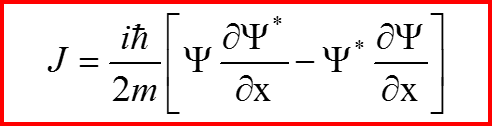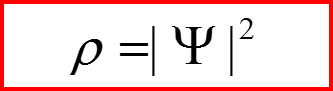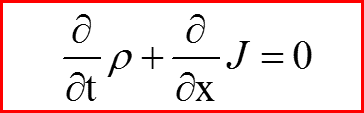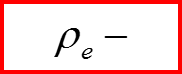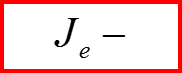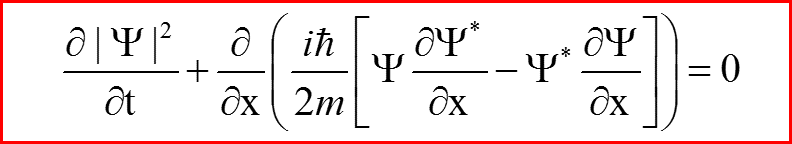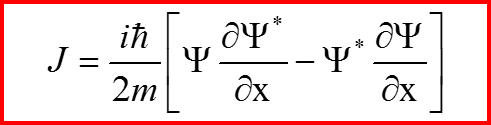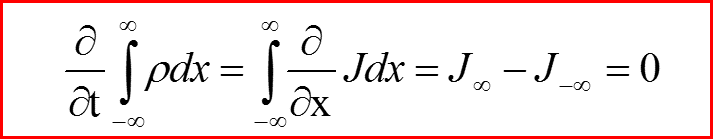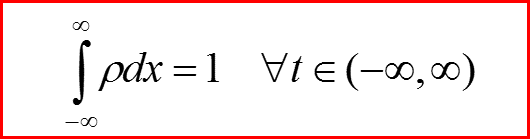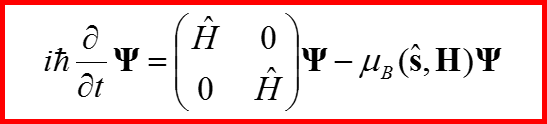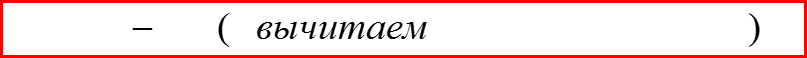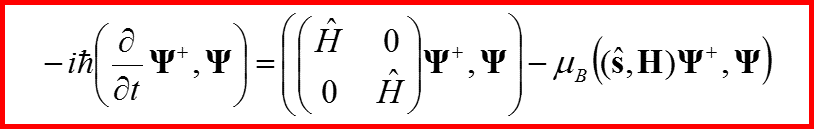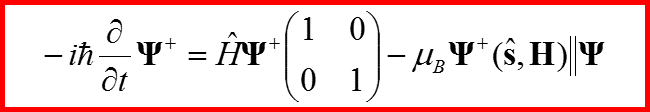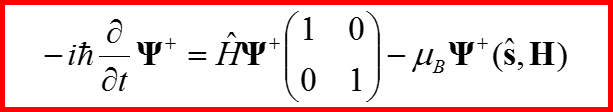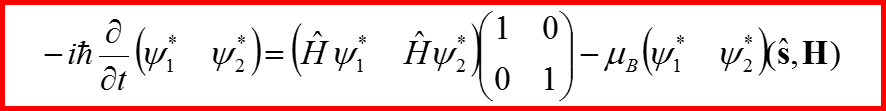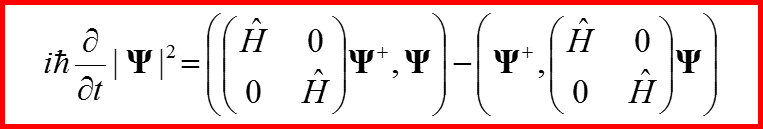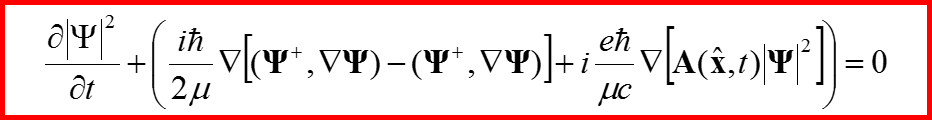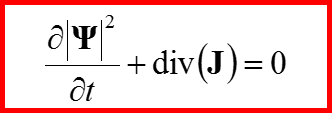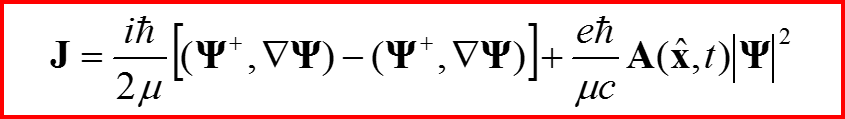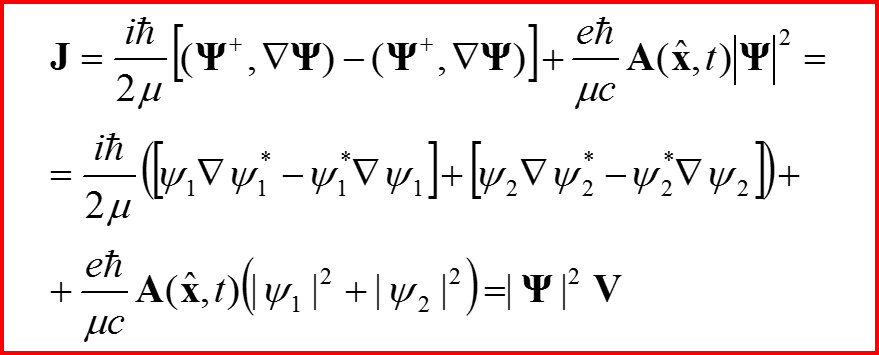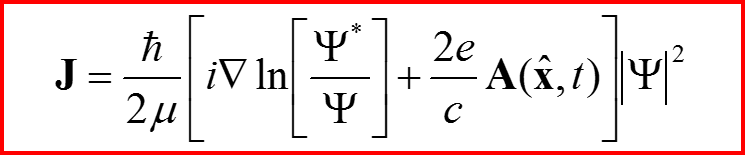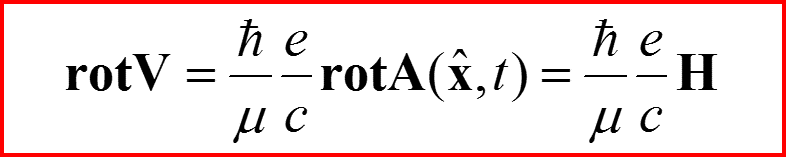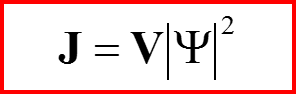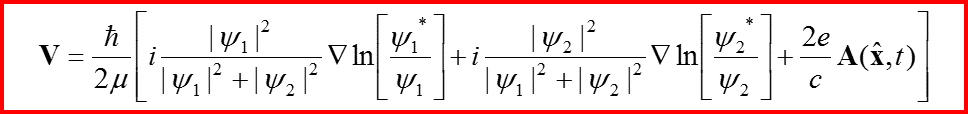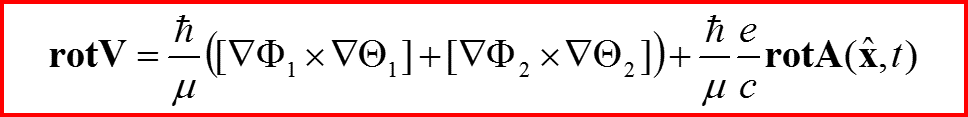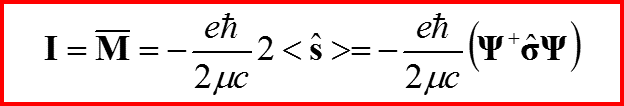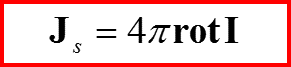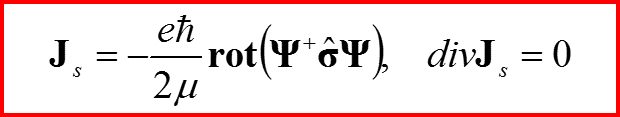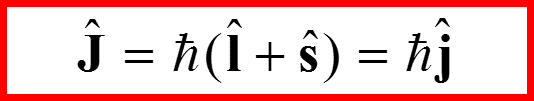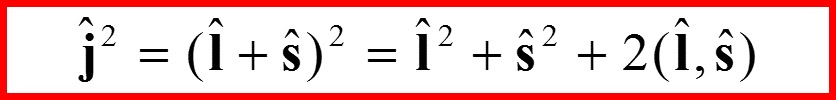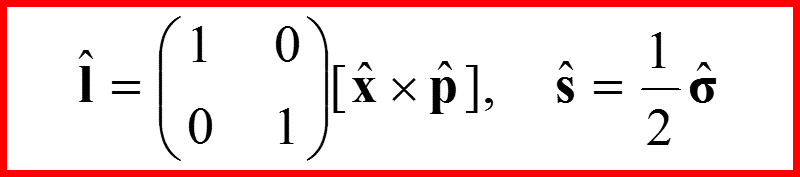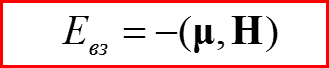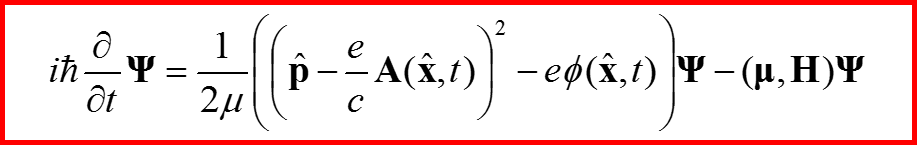Уравнение паули для спинового взаимодействия

Теория спина. Собственный механический момент электрона

Страницы работы

Содержание работы

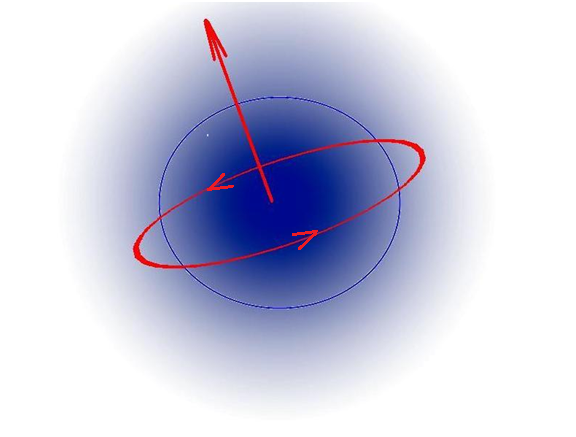
Что такое собственный механический момент электрона?

Экспериментальные основания теории спина

Как проявляется спин?

I. Формула Гаудсмита-Уленбека

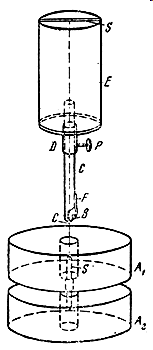
Общая схема эксперимента Эйнштейна-Де Гааза

I. Формула Гаудсмита-Уленбека

Вандер Иоганнес деГааз 1878-1960

Альберт Эйнштейн 1879-1955

I. Формула Гаудсмита-Уленбека

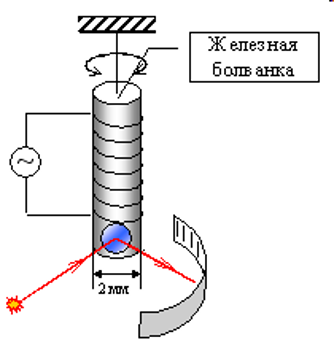
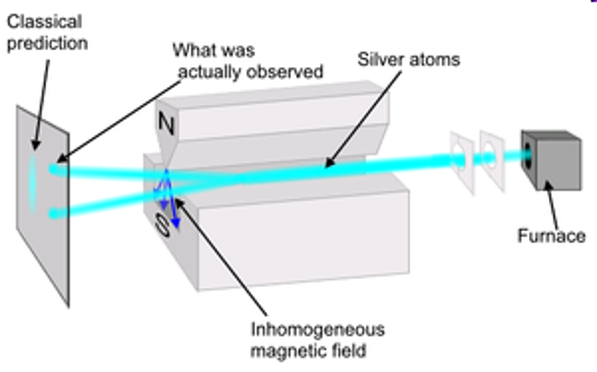
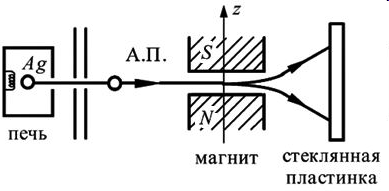
Общая схема эксперимента Штерна-Герлаха (1921-1922)

Отто Штерн 1888-1969

Вальтер Герлах 1889-1979

I. Формула Гаудсмита-Уленбека

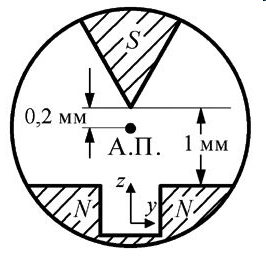
Поперечное сечение магнита

I. Формула Гаудсмита-Уленбека

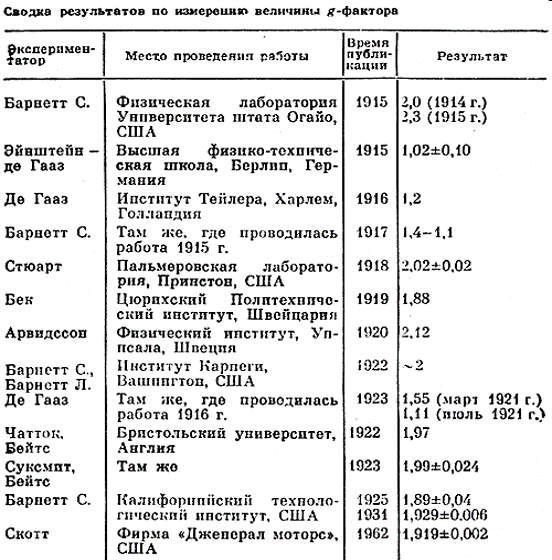
g – называется g-фактором. Для электрона g=2

I. Формула Гаудсмита-Уленбека

Уленбек, Джордж Юджин 6 декабря 1900, Батавия, Голландская Ост-Индия (ныне Джакарта, Индонезия)

Гаудсмит, Сэмюэл Абрахам 11 июля 1902, Гаага — 4 декабря 1978, Рино, Невада

Описание спиновых состояний

Чем отличаются спиновые состояния от состояний с фиксированным орбитальным числом?

II. Описание спиновых состояний

Результат экспериментов относительно магнитного момента электрона сводится к тому, что у электрона есть внутренний момент, который в проекции на заданную ось может принимать только два значения sz =1/2 и sz=-1/2

II. Описание спиновых состояний

Это означает, что в потоке электронов при одинаковых внешних условий есть электроны с волновой функцией Ψ1= Ψ(x,y,z,t,s=1/2) и Ψ2= Ψ(x,y,z,t,s=-1/2). Вероятность найти электрон в точке (x,y,z) в момент времени t равна: P=|Ψ1|2+|Ψ2|2 (Формула сложения вероятностей для несовместных событий)

II. Описание спиновых состояний

Волновая функция частицы — спинор:

ψ1 — волновая функция электрона со спином sz=1/2

ψ2 — волновая функция электрона со спином sz=-1/2.

II. Описание спиновых состояний

Скалярное произведение в спинорном пространстве:

II. Описание спиновых состояний

Общий вид оператора, действующего на спинорные волновые функции имеет следующий вид:

II. Описание спиновых состояний

Оператор спина. Матрицы Паули

Как устроен оператор спина?

III. Оператор спина

Все операторы, связанные с внутренним состоянием электрона должны быть матрицами размерности 2×2

III. Оператор спина

Спин – аналог орбитального момента!

Поэтому для него должны выполнятся аналогичные коммутационные соотношения!!

III. Оператор спина

Компоненты оператора спина должны представляться матрицами 2×2

Эти матрицы должны удовлетворять коммутационным соотношениям алгебры вращений!!

III. Оператор спина

Введем следующее соглашение!

Для оси, которую будем называть осью z Состояния с фиксированной проекцией на эту ось будем описывать спинорами:

III. Оператор спина

Следовательно! Оператор проекции спина на ось z должен быть диагональной матрицей и иметь собственные значения s=1/2 и s=-1/2

III. Оператор спина

Проверяем выполнение соглашения!

III. Оператор спина

Квадраты матриц проекций спина пропорциональны единичной матрице!

Поскольку sx=±1/2 и sy=±1/2, то

III. Оператор спина

Представим матрицы проекций спина в виде!

Матрицы σx σy σz матрицами Паули!

III. Оператор спина

Для матриц Паули коммуnационные соотношения выглядят так:

Для матриц σx σy σz получаем:

III. Оператор спина

III. Оператор спина

III. Оператор спина

Для трехмерного евклидова пространства метрический тензор gαβ равен символу Кронеккера!! gαβ= δαβ

III. Оператор спина

III. Оператор спина

III. Оператор спина

Матрица σx – эрмитова.

III. Оператор спина

III. Оператор спина

Матрицы Паули φ=0; χ=-π/2

III. Оператор спина

Компоненты оператора спина

IV. Уравнение Паули

Уравнение Шредингера для частицы со спином в отсутствии магнитного поля имеет вид:

IV. Уравнение Паули

Уравнение Шредингера для частицы без спина в магнитном поле имеет вид:

Спин – проявление собственного магнитного момента! Чему равна энергия взаимодействия частицы с магнитным моментом с магнитным полем?

IV. Уравнение Паули

Энергия взаимодействия магнитного момента μ с полем H имеет вид:

Здесь Ψ – спинор.

IV. Уравнение Паули

Называется уравнением Паули!!

IV. Уравнение Паули

IV. Уравнение Паули

IV. Уравнение Паули

В магнитном поле направление магнитного момента электрона изменяется. Поэтому изменяется вид спинора.

VI. Закон сохранения потока вероятностей

VI. Закон сохранения потока вероятностей

VI. Закон сохранения потока вероятностей

VI. Дифференциальный закон сохранения

Пример: Закон сохранения заряда

плот ность заряда

VI. Закон сохранения потока вероятностей

называется законом сохранения плотности вероятности, а величина

называется потоком вероятности

VI. Дифференциальный закон сохранения

Нормировка плотности вероятности сохраняется!

Ток, создаваемый частицей со спином

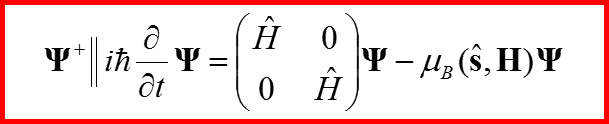
V. Сохранение вероятности для уравнения Паули

V. Сохранение вероятности для уравнения Паули

Вычислим правую часть по аналогии с бесспиновым гамильтонианом.

V. Сохранение вероятности для уравнения Паули

V. Сохранение вероятности для уравнения Паули

V. Сохранение вероятности для уравнения Паули

II. Закон сохранения потока вероятности (Лекция XII)

V. Сохранение вероятности для уравнения Паули

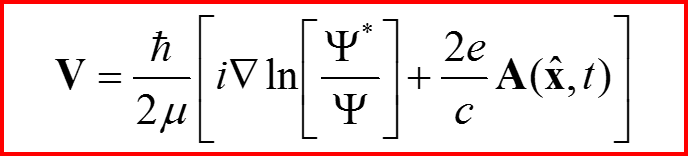
Скорость гидродинамического потока

V. Сохранение вероятности для уравнения Паули

V. Сохранение вероятности для уравнения Паули

Следовательно! Вместо намагничивания можно ввести ток намагничивания Js

Ток чисто вихревой!

Частица со спином в магнитном поле

Чем отличается эффект Зеемана для частиц со спином?

IV. Свойства квадрата полного момента

Оператор полного момента J:

IV. Свойства квадрата полного момента

IV. Свойства квадрата полного момента

Здесь Ψ – спинор.

IV. Свойства квадрата полного момента

Для матриц Паули коммуnационные соотношения выглядят так:

ПА́УЛИ УРАВНЕ́НИЕ

ПА́УЛИ УРАВНЕ́НИЕ, урав­не­ние не­ре­ля­ти­ви­ст­ской кван­то­вой ме­ха­ни­ки, опи­сы­ваю­щее дви­же­ние за­ря­жен­ной час­ти­цы со спи­ном 1 / 2 (напр., элек­тро­на) во внеш ­нем элек­тро­маг­нит­ном по­ле. Пред­ло­же­но В. Пау­ли в 1927.