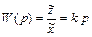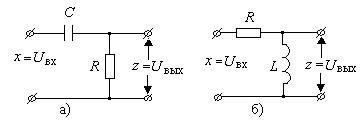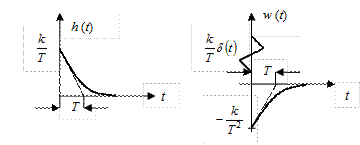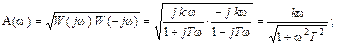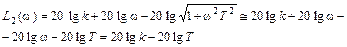Уравнение передаточной функции дифференцирующего звена

Дифференцирующее звено.

Различают идеальное и реальное дифференцирующие звенья.

Идеальное дифференцирующее звено характеризуется уравнением

, (2.13)

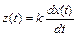
или в операторной форме

.

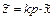
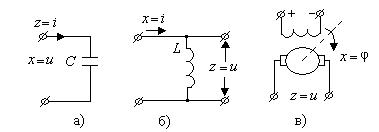
Примерами такого звена могут служить электрическая емкость (рис. 29 а), индуктивность (б), тахогенератор (в).

Рис.2.17. Примеры идеальных дифференцирующих

В самом деле, уравнения для тока в емкости

,

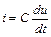
напряжения на индуктивности

,

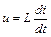
и напряжения на зажимах тахогенератора постоянного тока

,

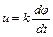
совпадают по форме с уравнением идеального дифференцирующего звена.

Из уравнения (8) получается передаточная функция идеального дифференцирующего звена

и, соответственно, частотная передаточная функция

.

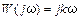
Для нахождения переходной характеристики идеального дифференцирующего звена воспользуемся соотношением

,

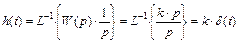
а весовая функция звена может быть получена следующим образом

.

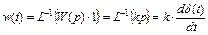
При известной частотной передаточной функции W(jω) АЧХ и ФЧХ звена легко находятся

.

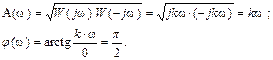
На рис. 30 построены эти зависимости. На этом же рисунке, по значениям A(ω) и φ(ω) получена АФХ звена W(jω), которая проходит по положительной полуоси ординат. Это обусловлено тем обстоятельством, что для любой частоты 0 ≤ .

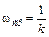
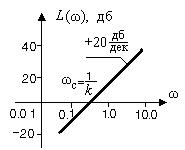
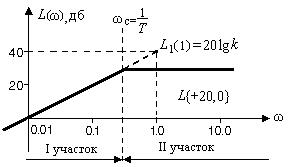
ЛАЧХ идеального дифференцирующего звена приведена на рис. 2.19.

Рис. 2.19. ЛАЧХ идеального дифференцирующего

Однако практически осуществить идеальное дифференцирующее звено, строго удовлетворяющее уравнению (8), не представляется возможным. Поэтому применяются звенья, выполняющие дифференцирующее действие более или менее приближенно. Такие звенья называются реальными дифференцирующими звеньями. Процессы в таких звеньях описываются дифференциальным уравнением вида

,

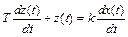
или в Лапласовой форме

. (2.14)

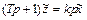
Примерами таких звеньев могут служить, например, четырехполюсники (рис. 2.20).

Рис. 2.20. Примеры реальных дифференцирующих звеньев.

Из уравнения (2.14) найдется передаточная функция звена

. (2.15)

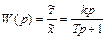
Переходную характеристику звена h(t) можно, как уже указывалось, определить по формуле:

. (2.16)

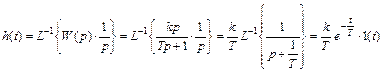
Весовую функцию звена найдем, исходя из выражения

.

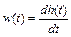
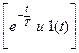
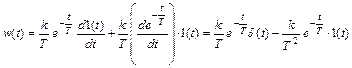
Поскольку h(t) – сложная функция, содержащая два сомножителя, зависящих от t , то

.

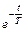
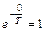
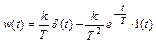
Так как первое слагаемое этого выражения равно нулю при t ≠ 0, ибо δ(t) = 0 при t ≠ 0, то сомножитель имеет смысл рассматривать только при t = 0, а в этом случае , и окончательно выражение для w(t) имеет вид

.

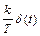
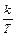
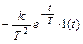
Таким образом, получается, что весовая функция реального дифференцирующего звена w(t) состоит из двух составляющих. Первая составляющая δ – функция с площадью расположена на оси ординат, а вторая – экспонента, рассматриваемая для t ≥0. Переходная h(t) и весовая w(t) функции приведены на рис. 33 а) и б), соответственно.

Рис. 2.21. Временные характеристики реального дифференциального звена.

Частотная передаточная функция W(j ) найдется из (2.3)

.

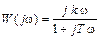
φ 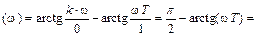φ₁(ω) – φ₂(ω)

Имея в виду, что при очень большой частоте, т.е. при → ∞, в подкоренном выражении для A( ) можно пренебречь первым слагаемым по сравнению со вторым, получается:

,

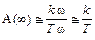
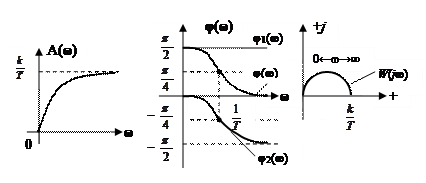
построим АЧХ и ФЧХ реального дифференциального звена, а по ним и АФХ (рис. 2.22)

Рис. 2.22. АЧХ (а), ФЧХ (б) и АФХ (в) реального дифференцирующего звена.

Выражение для точной ЛАЧХ звена имеет вид

.

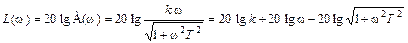
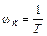
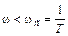
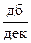
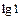
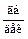
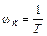
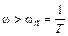
Как видно из (10) звена имеет одну постоянную времени Т и, значит, одну сопрягающую частоту [c -1 ]. Эта частота _с разобьет ось частот на два участка (рис.34)

или T * вычислим по этой формуле L₁( * ) и через эту точку проведем первую асимптоту с наклоном +20 . Удобнее всего брать * =1 (тогда 20 = 0), независимо от того, на I-м или II-м участках расположена эта частота. Затем через точку L₁( =1) проводят на I участке первую асимптоту с наклоном +20 до пересечения с вертикальной линией, проходящей через .

или T>1.

Тогда выражение для второй асимптоты получится из L( ), если в подкоренном выражении пренебречь первым слагаемым по сравнению со вторым

Это линия, не зависящая от частоты, т.е. проходящая параллельно оси абсцисс через конечную точку первой асимптоты.

Рис. 35. ЛАЧХ реального дифференцирующего звена.

Физическая реализация звена.

ЛЕКЦИЯ 5.

Дифференцирующее звено

Передаточная функция.

Передаточная функция дифференцирующего звена имеет вид:

W(s) = T·s где T – постоянная времени (время дифференцирования).

Математическое описание звена.

Дифференцирующее звено описывается уравнением, в котором встречается производная от входного сигнала:

Это не дифференциальное уравнение, поскольку входной сигнал х(t) и его производные полагаются заранее известными.

Физическая реализация звена.

Сразу отметим, что идеальное дифференцирующее звено физически нереализуемо. Вообще, любая передаточная функция с порядком числителя большим порядка знаменателя является физически нереализуемой. Укажем, какие факторы могут воспрепятствовать физической реализуемости:

§ нарушение причинности – выходной сигнал появляется раньше входного;

§ нереализуемая частотная характеристика, например, не стремящаяся к нулю при бесконечно больших частотах;

§ появление на выходе бесконечных значений сигналов при подаче физически реализуемых сигналов.

Строго говоря, физически нереализуемой является и ПФ с порядком числителя равным порядку знаменателя. Как мы видели ранее, даже идеальный усилитель не может быть физически реализован, не говоря уже об идеальном дифференцирующем звене, так как в обоих случаях АЧХ не стремятся к нулю при росте частоты.

Поскольку идеальное дифференцирующее звено физически нереализуемо, при этом сама операция дифференцирования часто встречается при описании процессов разной природы, то на практике часто используют «нетиповое» реальное дифференцирующее звено.Реальное дифференцирующее звено является соединением двух типовых звеньев — идеального дифференцирующего и инерционного, которые вместе приближённо описывающих операцию дифференцирования. Передаточная функция реального дифференцирующего звена имеет вид:

W(s) = T₁s/(T₂s + 1), где T₁ – постоянная времени дифференцирующей составляющей (время дифференцирования), а T₂ – постоянная времени апериодической составляющей. При малых значениях T₂, т.е. когда инерционность апериодического звена мала, составляющей T₂s в знаменателе передаточной функции можно пренебречь, тогда мы получим приближенную передаточную функцию идеального дифференцирующего звена:

Такое звено хорошо работает при низких частотах. Максимальная частота, при которой реальное дифференцирующее звено еще работает «почти как идеальное» равна:

Примерами дифференцирующего звена являются дифференцирующая цепочка, дифференцирующий трансформатор, операционный усилитель в режиме дифференцирования.

Переходная функция.

h(t) = L -1 [W(s)/s] = L -1 [T] = T·δ(t)

Таким образом, реакция дифференцирующего звена на ступенчатую функцию – это короткий импульс.

Весовая функция.

w(t) = L -1 [W(s)] = L -1 [T·s] = T·dδ(t)/dt

Переходную и весовую функцию дифференцирующего звена трудно изобразить графически, и тем более сложно представить, каков отклик (реакция) этого звена на входное воздействие. Поэтому рассмотрим отклик дифференцирующего звена на линейное (нарастающее) входное воздействие:

у(t) = L -1 [W(s)·Х(s)] = L -1 [T·s/s 2 ] = L -1 [T/s] = T·1(t).

Другими словами, если на вход дифференцирующего звена подать линейно нарастающий сигнал, то в момент подачи сигнала на выходе мы будем иметь скачок выходного сигнала с 0 до T.

Частотные характеристики.

Рис. 5.1. АФЧХ, ЛАХ и ЛФХ дифференцирующего звена.

W(jω) = T·j·ω = 0 + Tω·j

φ(ω) = arctg(Tω/0) arctg(∞) = π/2

L(ω) = 20lg[A(ω)] = 20lg(Tω).

Как видим, частотные характеристики дифференцирующего звена обратны частотным характеристикам интегрирующего звена.

Форсирующее звено I-ого порядка

Передаточная функция.

Передаточная функция форсирующего звена I-ого порядка имеет вид:

W(s) = K·(Ts + 1) где K – коэффициент усиления; T – постоянная времени.

Дифференцирующее звено

В теории автоматического регулирования различают реальное дифференцирующее звено и идеальное дифференцирующее звено.

Идеальное дифференцирующее звено

Давайте для начала рассмотрим идеальное дифференцирующее звено, типовое дифференциальное уравнение которого имеет вид:

Операторная форма записи имеет следующий вид:

Передаточная функция идеального дифференцирующего звена имеет вид:

Аналитическое выражение вектора амплитудо-фазовой характеристики (АФХ) для идеального дифференцирующего звена имеет вид:

В последнем выражении при изменении частоты от 0 до ∞ легко построить график вектора АФХ идеального дифференцирующего звена (рисунок 1 а)). Конец вектора АФХ перемещается по положительной мнимой полуоси комплексной плоскости от начала координат, уходя при ω = ∞ в бесконечность.

Идеальное дифференцирующее звено имеет своеобразную переходную функцию (рисунок 1 б)). Выходной сигнал данного звена пропорционален тангенсу угла наклона вектора АФХ, то есть первой производной. Угол равен +90 0 в момент подачи входного воздействия, а tg(+90 0 ) = +∞, но далее входное воздействие становится равным единице, при этом угол наклона изменяется на -90 0 , а tg(-90 0 ) = -∞.

Откуда следует, что в момент подачи входного сигнала выходной сигнал идеального дифференцирующего звена примет значение +∞. Тут же из +∞ вычитается -∞ и выходной сигнал снова принимает нулевое значение (рисунок 1б)).

Примером электрической реализации идеального дифференцирующего звена может послужить электрическая цепь, состоящая из резистора R и конденсатора С, при этом резистор R обладает сверхпроводимостью (R = 0). Схема данной RC цепочки показана на рисунке 1 в).

Реальное дифференцирующее звено

Типовое дифференциальное уравнение для реального дифференцирующего звена имеет вид:

Операторная форма данного уравнения:

х_вых (р) можно вынести за скобки:

После чего получить аналитическое выражение передаточной функции реального дифференцирующего звена:

Совершив замену p на jω в передаточной функции, получим аналитическое выражение вектора АФХ для данного звена:

Изменяя частоту после ω проведенных алгебраических преобразований от 0 до ∞ в мнимой in(ω) и действительной m(ω) частях вектора амплитудо- фазовой характеристики (АФХ), построим годограф реального дифференцирующего звена (рисунок 2 а).

В знаменателе m(ω) при ω = ∞ единицу можно отбросить, тогда можно сократить дробь:

Отсюда получим, что m(ω) = k / T₀.

Следовательно, графиком вектора АФХ реального дифференцирующего звена будет полуокружность в первом квадранте комплексной плоскости, диаметр которой будет равен k / T₀.

На рисунке 2 б) показана переходная функция реального дифференцирующего звена. На рисунке видно, что при подаче возмущения в виде единичного скачка выходной сигнал мгновенно увеличится на величину k / T₀, после чего начнет плавно уменьшаться (по нелинейному закону) пока его значение не станет равным нулю. По переходной характеристике не сложно определить коэффициенты k и T₀ передаточной функции. Сначала с помощью касательной находят значение T₀, после чего умножив ординату величины k / T₀ на T₀, определяют значение k.

В качестве примера электрической реализации реального дифференцирующего звена может послужить RC цепочка, в которой сопротивление R ≠ 0, что вполне может быть собрано из существующих элементов.