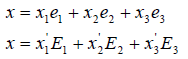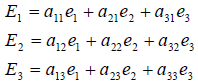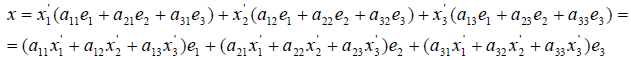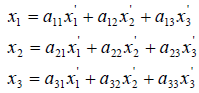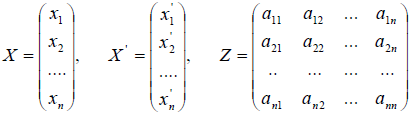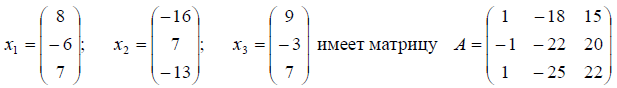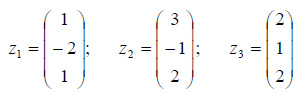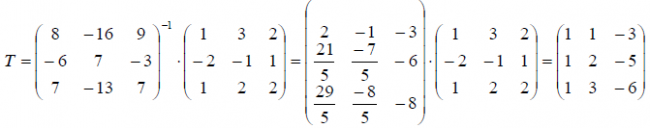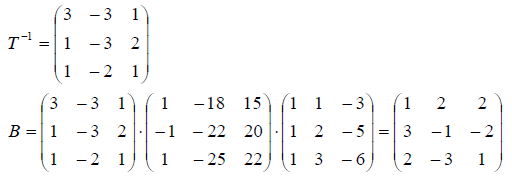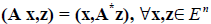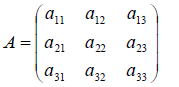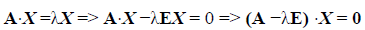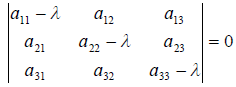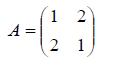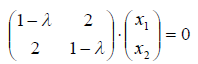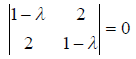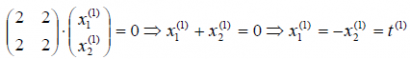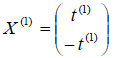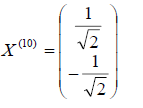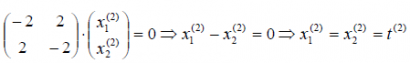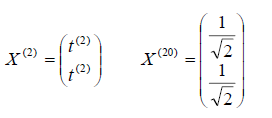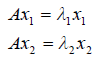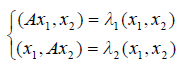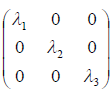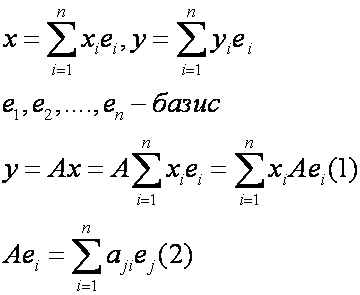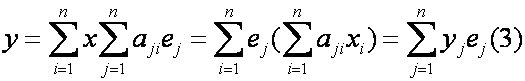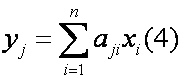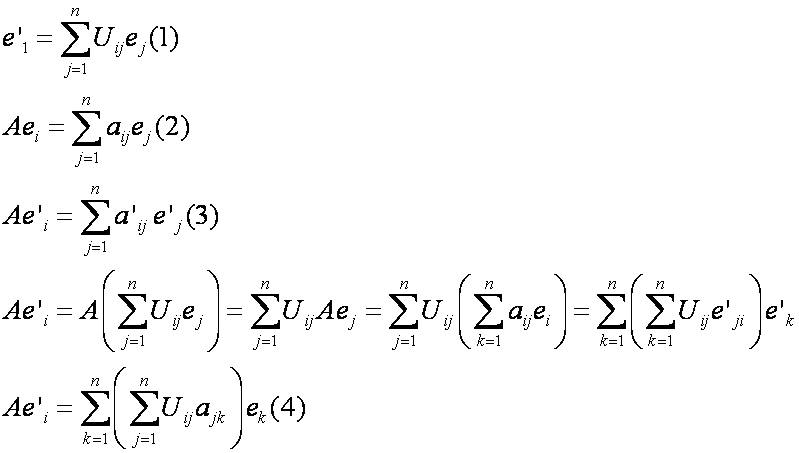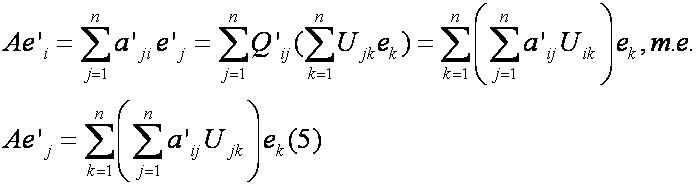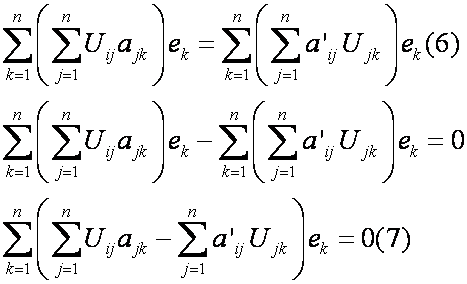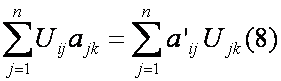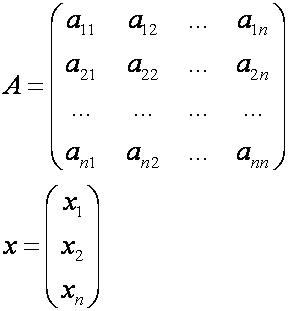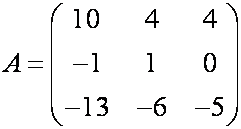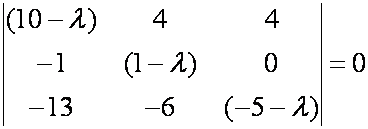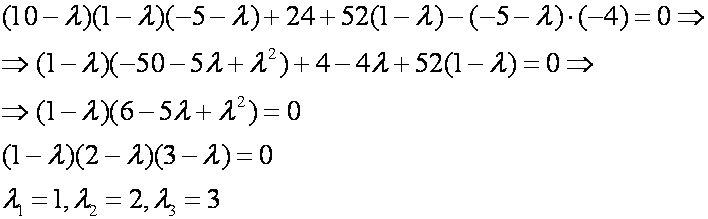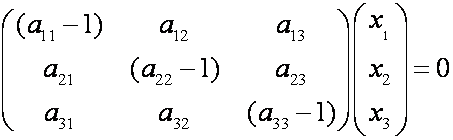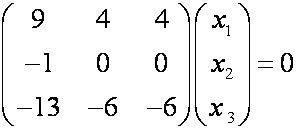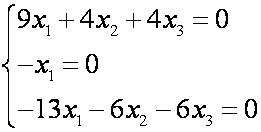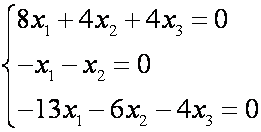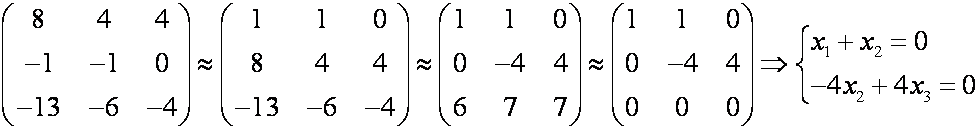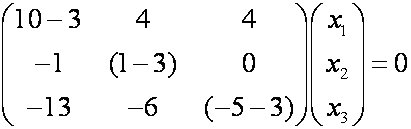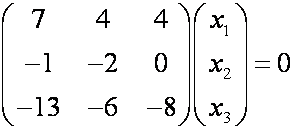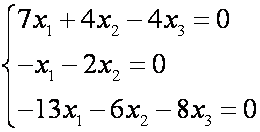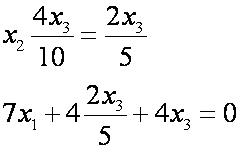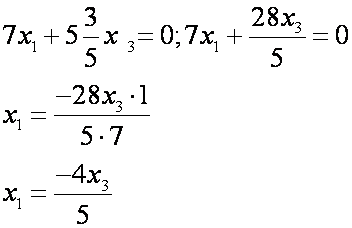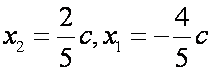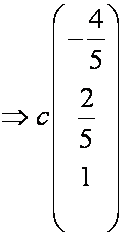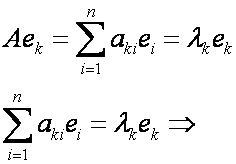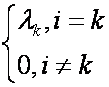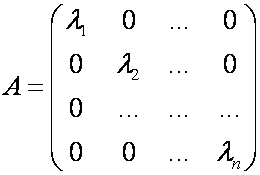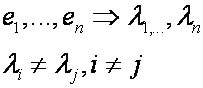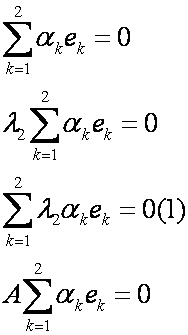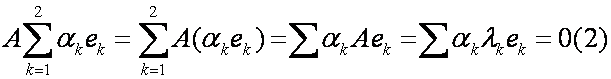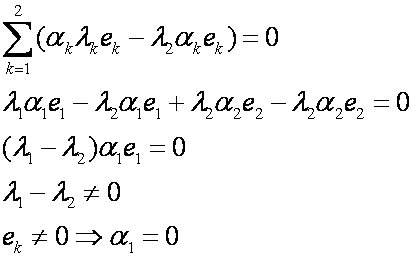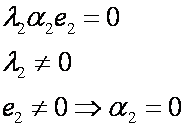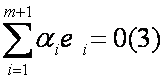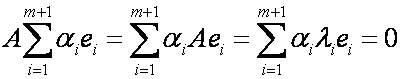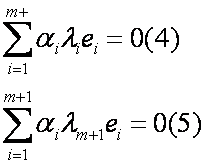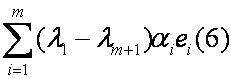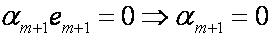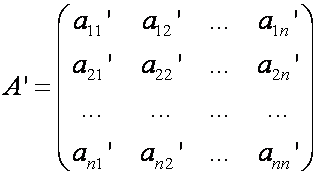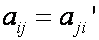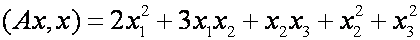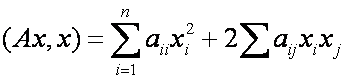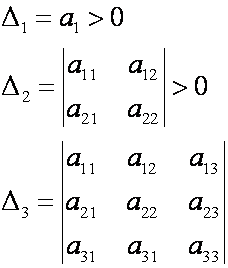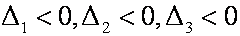Уравнение перехода к новому базису

Координаты и преобразования координат в линейном пространстве

Координаты векторов в данном базисе линейного пространства

Пусть — базис линейного пространства . Каждый вектор можно разложить по базису (см. теорему 8.1), т.е. представить в виде , причем коэффициенты в разложении определяются однозначно. Эти коэффициенты называются координатами вектора в базисе (или относительно базиса ). Координаты вектора — это упорядоченный на бор чисел, который представляется в виде матрицы-столбца и называется координатным столбцом вектора (в данном базисе). Вектор и его координатный столбец обозначаются одной и той же буквой полужирной или светлой соответственно.

Если базис (как упорядоченный набор векторов) представить в виде символической матрицы-строки , то разложение вектора по базису можно записать следующим образом:

Здесь умножение символической матрицы-строки на числовую матрицу-столбец производится по правилам умножения матриц.

При необходимости, если речь идет о разных базисах, у координатного столбца указывается обозначение базиса, относительно которого получены координаты, например, — координатный столбец вектора в базисе .

Из теоремы 8.1 следует, что равные векторы имеют равные соответствующие координаты (в одном и том же базисе), и наоборот, если координаты векторов (в одном и том же базисе) соответственно равны, то равны и сами векторы .

Линейные операции в координатной форме

Пусть — базис линейного пространства , векторы и имеют в этом базисе координаты и соответственно, т.е.

Складывая эти равенства, получаем .

т.е. при сложении векторов их координаты складываются .

Умножая второе равенство в (8.7) на число , получаем

т.е. при умножении вектора на число все его координаты умножаются на это число .

Другими словами, сумма векторов имеет координаты , а произведение имеет координаты . Разумеется, что все координаты получены в одном базисе .

1. Нетрудно показать, что координатный столбец линейной комбинации векторов равен линейной комбинации координатных столбцов этих векторов.

2. Если система векторов линейно зависима (линейно независима), то их координатные столбцы, полученные относительно одного базиса, образуют линейно зависимую (соответственно, линейно независимую) систему. Это следует из равносильности равенств и . Например, если в этих равенствах не все коэффициенты равны нулю, т.е. система векторов и система их координатных столбцов линейно зависимы одновременно.

3. Все свойства линейной зависимости и линейной независимости векторов переносятся без изменений на их координатные столбцы, полученные в одном и том же базисе. И наоборот, свойства для матриц-столбцов, переносятся на векторы, если матрицы-столбцы считать их координатными столбцами.

4. Выбрав в n-мерном вещественном линейном пространстве некоторый базис, можно установить взаимно однозначное соответствие: каждому вектору поставить в соответствие его координатный столбец (в вы бранном базисе), и наоборот, каждому координатному столбцу поставить в соответствие вектор. Другими словами, любой фиксированный базис n-мерного вещественного линейного пространства позволяет установить взаимно однозначное соответствие между всеми векторами вещественно го пространства и всеми столбцами n-мерного арифметического пространства . Это соответствие обозначается . Для n-мерного комплексного линейного пространства аналогичное взаимно однозначное соответствие устанавливается с пространством .

Преобразование координат вектора при замене базиса

Пусть заданы два базиса пространства и . Базис будем условно называть «старым», а базис — «новым». Пусть известны разложения каждого вектора нового базиса по старому базису:

Записывая по столбцам координаты векторов в базисе , составляем матрицу:

Квадратная матрица , составленная из координатных столбцов векторов нового базиса в старом базисе , называется матрицей перехода от старого базиса к новому. При помощи матрицы перехода (8.9) формулы (8.8) можно записать в виде:

Умножение символической матрицы-строки на матрицу перехода в (8.10) производится по правилам умножения матриц.

Пусть в базисе вектор имеет координаты , а в базисе — координаты , т.е.

Подставляя в правую часть последнего равенства выражение (8.10), получаем — два разложения вектора в одном и том же базисе . Коэффициенты этих разложений должны совпадать (по теореме 8.1), так как это координаты одного и того же вектора в одном базисе. Поэтому

Формула (8.11) устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе .

Пример 8.3. В пространстве многочленов степени не выше второй даны две системы многочленов:

Доказать, что каждая система является базисом пространства . Найти матрицу перехода от базиса к базису . Определить координаты квадратного трехчлена относительно базисов и .

Решение. Система многочленов является стандартным базисом пространства . Докажем, что система является базисом. По ступим следующим образом. Найдем координатные столбцы этих многочленов в стандартном базисе. Раскладывая по базису , получаем

Составим из этих столбцов матрицу . Ранг этой матрицы равен 3, так как . Следовательно, столбцы линейно независимы, тогда и многочлены линейно независимы (см. пункт 2 замечаний 8.5). Итак, многочлены являются базисом пространства , а матрица — искомая матрица перехода от базиса к базису . Осталось найти координаты многочлена в этих базисах. Раскладывая по базисам, находим

Проверим результат, вычисляя по формуле (8.11):

Свойства матрицы перехода от одного базиса к другому

1. Пусть имеются три базиса пространства и известны матрицы перехода: от базиса к базису ; от к ; от к . Тогда

Действительно, запишем связь (8.10) для данных базисов:

Подставляя первое выражение во второе равенство, получаем . Сравнивая с третьим равенством, приходим к (8.12).

2. Если — матрица перехода от базиса к базису , то матрица обратима и обратная матрица является матрицей перехода от базиса к базису . Координаты вектора в базисах и связаны формулами:

В самом деле, пусть — матрица перехода от базиса к базису . Учитывая, что матрица перехода от базиса к базису — единичная, применяем свойство 1 к трем базисам . Для трех базисов аналогично получаем: . Следовательно, .

3. Всякая обратимая квадратная матрица n-го порядка может служить матрицей перехода от одного базиса n-мерного линейного пространства к другому базису.

Пример 8.4. В двумерном арифметическом пространстве даны два базиса: и . Найти матрицу перехода от базиса к базису и координаты вектора в каждом из базисов.

Решение. Рассмотрим стандартный базис пространства . Находим координаты векторов в стандартном базисе. Раскладываем вектор

В стандартном базисе пространства координатный столбец совпадает с вектором . Для других векторов аналогично получаем . Из координатных столбцов составим матрицы перехода (8.9) от стандартного базиса к данным базисам и

По свойству 1 матриц перехода имеем . .По свойству 2: . Поэтому

В стандартном базисе пространства координатный столбец совпадает с вектором . Найдем координаты этого вектора в базисе (по свойству 2 матрицы перехода):

В самом деле, справедливо разложение

Найдем координаты вектора в базисе двумя способами

Полученный результат подтверждает разложение:

Замена базиса

Матрица преобразования координат

Возьмём в пространстве E n два различных базиса e 1 ,e 2 . e n и E 1 ,E 2 . E n

Рассуждение проведём для случая n = 3. Один и тот же вектор x относительно различных базисов имеет различные координаты. Можем написать:

Любой вектор второго базиса можем разложить по первому базису, т.е.

В силу единственности разложения по данному базису мы должны приравнять коэффициенты при векторах e 1 ,e 2 ,e 3 и полученные. Тогда

Введём в рассмотрение матрицы

Тогда полученные соотношения можно записать в матричном виде X = Z X .

Матрица Z называется матрицей преобразование координат при переходе от старого базиса к новому, т.е. от базиса e 1 ,e 2 . e n к базису E 1 ,E 2 . E n . Причём, столбцами матрицы преобразования координат являются координаты вектора нового базиса E 1 ,E 2 . E n относительно старого базиса e 1 ,e 2 . e n .

Изменение матрицы линейного оператора при переходе к новому базису

Пусть в пространстве E n определён линейный оператор A , т.е. y = A x

Или Y = A X , где X (x 1 ,x 2 . x n ) T и Y (y 1 ,y 2 . y n ) T матрицы-столбцы, со ставленные из координат векторов x и y относительно данного базиса n 1 ,e 2 . e n , A — матрица линейного оператора A .

Выберем в том же пространстве E n другой базис E 1 ,E 2 . E n . Относительно нового базиса матрица линейного оператора A будет иной. Обозначим через T матрицу преобразова ния координат, а через X и Y — одностолбцовые матрицы, составленные из координат векторов x и y относительно нового базиса, т.е.

Подставим полученное в общий вид, тогда получим: T Y = A T X

Умножая левую и правую части равенства слева на T -1 , получим: Y = T -1 A T X .

Итак, если в E n перейти к новому базису, то матрица линейного оператора также изменится и в самом общем случае будет равна T -1 A T .

Пример: Оператор A в базисе пространства E 3

Найти его матрицу в базисе

Решение: Матрица оператора в новом базисе находим по формуле B = T -1 AT , где T — матрица перехода от старого базиса к новому. Матрицу перехода находим по формуле T = X -1 Y .

Сопряженный и самосопряженный оператор

Пусть в вещественном евклидовом пространстве E n определён линейный оператор A

Определение 1. Оператор A * в вещественном евклидовом пространстве E n называ ется сопряженным по отношению к линейному оператору A в том же пространстве, если его матрица в любом ортонормированном базисе этого пространства является транспо нированной по отношению к матрице оператора A .

Свойства сопряженного оператора

1. E * = E, где E — тождественный оператор, т.е. оператор, матрица которого E единичная в E n

4. если A -1 существует, то (A -1 ) * = (A * ) -1 .

Определение 2. Линейный оператор A, определённый в вещественном евклидовом пространстве E n , называется самосопряженным, или симметрическим, если он cовпа дает со своим сопряженным оператором A * , т.е. если A * = A .

Матрица самосопряженного оператора совпадает с транспонированной в любом ортонормированном базисе, т.е. является симметричной относительно главной диагонали.

Свойства самосопряженного оператора

1. если A * = A , B * = B , то (A + B) * = A * + B * = A + B ;

2. если A — невырожденный самосопряженный оператор, то (A -1 ) * = (A * ) -1 = A -1 .

Доказательство. Действительно, если существует A -1 и кроме того A * = A , то в силу свойства 4 сопряженного оператора, получим (A -1 ) * = (A * ) -1 = A -1 ;

3. Если A — самосопряженный оператор в вещественном пространстве E n , то имеет место равенство:

Собственные векторы и собственные значения линейного оператора

Пусть A — линейный оператор. Пусть x 1 , где 1 некоторое подпространство прост ранства E n . Вектор y = A x может принадлежать подпространству 1 , а может и не принад лежать.

Определение. Подпространство 1 называется инвариантным по отношению к оператору A, если A x 1 , x 1 .

Определение. Ненулевой вектор x называется собственным вектором линейного оператора A, если найдётся такое число , что будет выполняться равенство A x = x . При этом число называют собственным значением (собственным числом) оператора A , соответствующим вектору x. Множество всех собственных значений оператора A называется его спектром.

Остановимся на отыскании собственных значений и собственных векто ров линейного оператора A. Рассмотрение проведём для случая n = 3. Итак, пусть в некотором базисе оператор A имеет матрицу

и пусть одностолбцовая матрица 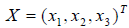соответствует вектору x. Тогда в силу определения

Дело свелось к решению системы линейных однородных уравнений, записанной в матричном виде. Очевидно, что эта система имеет ненулевое решение, если det(A E) = 0. Уравнение det(A E) = 0 называется характеристическим уравнением оператора A; многочлен det(A E) называется соответственно характеристическим многочленом оператора A. В координатной форме характеристическое уравнение выглядит так:

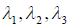
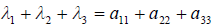
Решив его, найдём — собственные значения линейного оператора. Далее, для суммы диагональных элементов матрицы A, которую называют следом этой матрицы trA или следом оператор A (trA), справедлива формула . Кроме того, detA = 1 2 3 .

После того как найдены собственные значения линейного оператора A, остаётся подставить их по очереди в уравнение и найти соответствующие собственные векторы x (1) , x (2) , x (3)

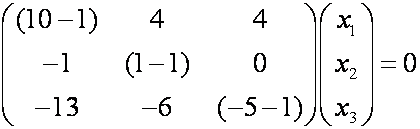
Пример: Найти собственные значения и собственные числа линейного оператора, матрица которого

Решение. По определения собственного вектора можем написать 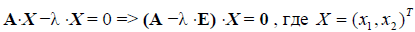— матрица – столбец, соответ ствующая искомому вектору x линейного оператора A;

В матричной форме получим:

Система однородная, следовательно, она имеет бесчисленное множество решений, если определитель системы равен нулю, т.е. имеем характеристическое уравнение:

Решая его, получим такие собственные значения 1 = 1; 2 = 3.

Найдём соответствующие собственные векторы.

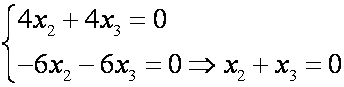
1) 1 = 1 подставим в уравнение, получим

где t (1) — некоторый параметр. Таким образом, имеем множество коллинеарных векторов, соответствующих первому собственному числу 1 = 1:

Этот вектор нетрудно пронормировать, тогда мы получим единичный собственный вектор, соответствующий первому собственному числу 1 = 1 т.е.

2) 2 = 3 подставим в уравнение, получим

В заключение заметим, что множество всех векторов y = A x , где x E n , называется областью значений линейного оператора A в E n , а множество всех векторов x 1 E n , таких, что A x = 0, называется ядром линейного оператора.

Свойства собственных чисел и собственных векторов самосопряженного оператора

Рассмотрим самосопряженный оператор A, определённый в вещественном евклидо вом пространстве E n . В силу определения матрица его A -симметрическая.

Теорема 1. Собственные числа самосопряженного оператора A есть вещественные числа.

Теорема 2. Собственные векторы, отвечающие двум различным собственным значениям самосопряженного оператора, ортогональны.

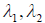
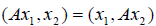
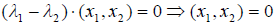
>Доказательство. Пусть — различные собственные значения самосопряженного оператора A, а x 1 , x 2 — соответствующие им собственные значения. Тогда

Но т.е. левые части равенств равны, следовательно, вычитая их почленно, получим: а это и означает, что собственные векторы x 1 , x 2 ортогональны.

Замечание. Так как собственные векторы самосопряженного оператора A ортогональны, их можно принять за базис линейного пространства, в котором определён этот линейный оператор. Поделив далее каждый вектор на его длину, мы получаем ортонор мированный базис.

Теорема 3. В базисе из единичных собственных векторов самосопряженного оператора матрица этого оператора диагональная, причём элементами диагонали являются её собственные числа.

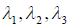
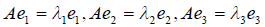
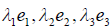
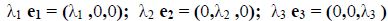
Доказательство. Доказательство проведём для случая n = 3. Пусть e 1 , e 2 , e 3 — единичные векторы самосопряженного оператора A относительно некоторого базиса линейного пространства 3 , отвечающие собственным значениям этого линейного оператора, т.е. . Примем векторы e 1 , e 2 , e 3 за базис линей ного пространства. Очевидно, что в этом базисе векторы имеют координаты:

. Следовательно, матрица A оператора A в базисе e 1 , e 2 , e 3 имеет вид:

Выбор такого базиса, в котором матрица линейного оператора имеет диагональный вид, называется приведением матрицы к диагональному виду.

6. ЛИНЕЙНЫЕ ОПЕРАТОРЫ

6.1 Понятие линейного оператора

О п р е д е л е н и е. Всякое правило, с помощью которого элементу х линейного пространства V ставится в соответствие некоторый элемент у линейного пространства W , называется оператором и обозначается А. Итак,

О п р е д е л е н и е. Оператор А называется линейным, если он удовлетворяет требованиям:

II . .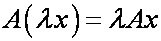

В случае n =1 (одномерное пространство) линейный оператор – это обычная линейная функция y = kx + b .

Нулевой оператор – это оператор 0( х)=0.

Единичный оператор I ( х)= x не изменяет элемента.

Противоположный оператор – это оператор (– A ).

О п р е д е л е н и е. Суммой операторов А и В называется оператор A + B , действующий по правилу (А+В)х=Ах+Вх.

Произведение операторов: (АВ)х=А(Вх).

Обратный оператор – это оператор, произведение которого с исходным дает единичный оператор.

6.2 Матричная форма записи линейных операторов

А в n – мерном линейном пространстве

Подставляем равенство (2) в выражение (1)

Из выражения (3) получаем

Из выражения (4) следует — элементы матрицы, поэтому выражение (4) можно представить у=Ах(5)

Равенство (5) представляет собой матричную форму записи линейного оператора, поэтому в дальнейшем вместо оператора А можно использовать матрицу А этого оператора.

6.3 Преобразование матрицы линейного оператора при переходе к новому базису

Нужно найти связь между матрицей А и А’

Переход осуществляется с помощью матрицы

Согласно выражению (3)

Так как левые части выражений (4) и (5) совпадают, то правые части тоже совпадают.

Выражение (7) представляет собой разложение некоторого вектора по базису е_к и этот вектор равен 0, отсюда все координаты вектора =0, т.е.

Выражение (8) представляет собой координатную форму записи произведения матриц.

Выражение (9) – матричная форма записи равенства (8)

Умножим равенство (9) слева на U -1

Выражение (10) определяет зависимость между матрицей оператора А в базисе е_к и матрицей этого же оператора в новом базисе, т.е определяет закон преобразования матрицы линейного оператора при переходе к новому базису.

Умножим выражение (9) справа на U -1

UAU -1 = A ` UU -1 (11)

Получить выражение (11) можно из выражения (10).

6.4 . Собственные значения и собственные векторы линейного оператора

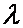
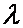
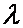
Опр. Число называется собственным значением линейного оператора Ф, если существует такой ненулевой вектор х, что Ах= х (1) или в матричной форме Ах= х (2)

Выражение (2) преобразуем

Ах= 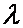Ix

I -единичный оператор

Ах- 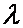ix =0

X ( A — 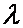I )=0 (3)
выражение (3) представляет собой матричную форму записи однородной системы линейных алгебраических уравнений. Однородная система линейных алгебраических уравнений имеет ненулевые решения, когда определитель этой системы равен нулю.

Det ( A — 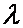I )=0 (4)

При этом ненулевые решения системы (3) называются собственными векторами оператора А, соответствующими собственному значению .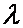

Выражение (4) называется характеристическим уравнением оператора А. Оно представляет собой многочлен порядка n относительно .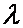

В координатной форме выражение (4) будет иметь вид:

П р и м е р. Найти собственные значения и собственные векторы линейного оператора с матрицы А.

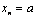
Р е ш е н и е. Составляем характеристическое уравнение. Для этого от диагональных элементов вычитаем 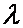и приравниваем к 0

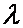
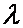
Находим собственные векторы, соответствующие собственному значению ₁ =1. для этого подставляем в выражение (3) ₁=1

Записываем это выражение в координатной форме

Решаем полученную систему любым способом

Находим собственные векторы 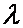₂=2

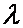
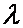
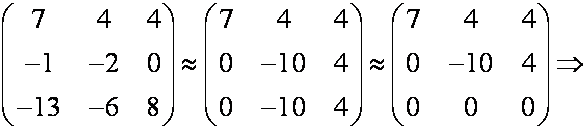
Найдем собственные векторы для ₃

₃ =3

Х₃ – свободная переменная, х₃=0, тогда

Для =3

Матрица линейного оператора в базисе, составленном из собственных векторов этого оператора, имеет диагональный вид.

Пусть _к, А е_к – соответствующие собственные векторы, т.е. Ае_к= _ке_к

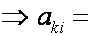
В качестве диагональных элементов берутся собственные значения этого оператора.

Собственные векторы, соответствующие различным собственным значениям, линейно независимы.

Доказательство справедливости этого утверждения с помощью метода математической индукции.

Согласно свойствам линейного оператора имеем:

Из выражения (2) вычтем (1)

Подставляем найденное значение в выражение (1)

выражение возможно лишь при

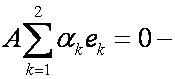
Если е₁,…,е_м линейно независимы, то е₁,…,е_м+1 – линейно независимы.

Предположим, что м собственных векторов линейно независимы, тогда м+1 линейно независимы.

Найдем разность выражений (4) и (5)

поэтому в выражении (6), (7) i =1,2…, m , тогда выражение (3) с учетом (7) преобразуется к виду

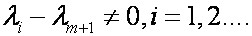
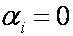
Вывод: в выражении (3) все коэффициенты равны 0, поэтому 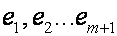линейно независимы, следовательно, собственные векторы соответственно различны собственным значениям, линейно независимы.

6.5 Самосопряженные линейные операторы

Опр. Оператор А’ называется сопряженным к оператору А, если для любых элементов х,у линейного пространства выполняется условие (А х,у)=(х,А’у)

Матрица сопряженного оператора является транспонированной матрицей, в чем легко убедиться непосредственным вычислением.

Всякий линейный оператор имеет единственный сопряженный оператор, т.к. всякая матрица имеет единственную транспонированную.

Основные свойства транспонированной матрицы:

2. ( ,A)’= A

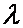
Справедливость первых четырех свойств следует непосредственно из определения оператора и сопряженного оператора.

Докажем пятое свойство.

Согласно определению имеем:

Сравниваем выражения (1) и (2)

( x ,( AB )’ y )=( x , B ’ A ’ y ), ( AB )’= B ’ A ’

Опр. Оператор А, равный своему сопряженному А’ называется самосопряженным.

Матрица самосопряженного оператора симметричная, т.е. a_ij = a_ji

Основные свойства самосопряженных операторов:

1. собственные значения самосопряженного оператора – все вещественные и различные.

2. собственные векторы, соответствующие различным собственным значениям взаимно ортогональны.

6.6. Квадратичные формы

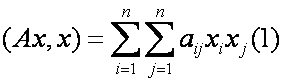
Опр. Квадратичной формой называется выражение вида:

Запишем матрицу этой квадратичной формы

Опр. Квадратичная форма называется положительно определенной, если для любого х квадратичная форма положительна. Квадратичная форма называется отрицательно определенной, если для любого х квадратичная форма отрицательна.

Квадратичная форма называется знакопеременной, если для одних элементов х она положительна, а для других элементов у она отрицательна.

Критерий Сильвестра. Квадратичная форма будет положительно определенной, если все угловые миноры матрицы А положительны, т.е. если

Квадратичная форма называется отрицательно определенной, если знаки угловых миноров матрицы А чередуются, причем

Матрица А в базисе, составленном из собственных векторов имеет диагональный вид. , причем диагональными элементами являются собственные элементы этой матрицы. Это значит, что если матрицу квадратичной формы привести к диагональному виду, то квадратичная форма такой матрицы примет простой вид: , (1), т.е. будет содержать квадраты элементов

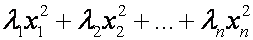
Выражение (1) называется каноническим видом квадратичной формы.