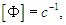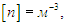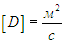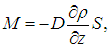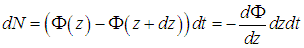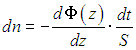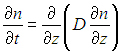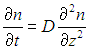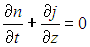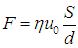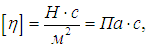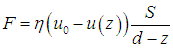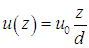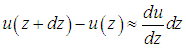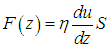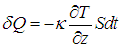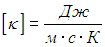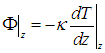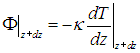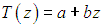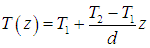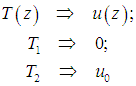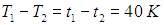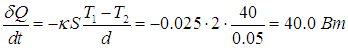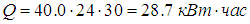4.2. Законы процессов переноса
Если газ выведен из состояния равновесия, то в нем возникают процессы, стремящиеся вернуть систему в равновесное состояние. Например, разные части системы имеют разные температуры или концентрации частиц. Соответственно, температуры или концентрации стремятся выровняться (за счет теплового движения молекул), что сопровождается передачей (переносом) тех или иных физических величин от одной части системы к другой. Такие процессы называются явлениями переноса. Эти явления имеют много общего и классифицируются по тому признаку, какая именно физическая характеристика «переносится» из одной части системы в другую.
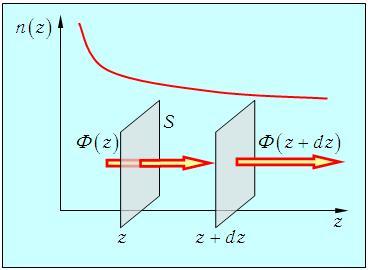
Диффузия. Пусть в системе имеются молекулы, концентрация которых n(z) зависит от координаты z. Мысленно поместим в точке с координатой z квадратик площадью S, ортогональный оси z. В системе происходит процесс выравнивания концентрации n частиц, сопровождающийся их переносом в направлении убывания n. Эксперимент показал, что через площадь S за единицу времени проходит количество частиц
где D определяется свойствами системы и называется коэффициентом диффузии. Величина Ф (поток частиц — число частиц в единицу времени) имеет размерность
размерность концентрации частиц
и поэтому размерность коэффициента диффузии
Отрицательный знак в законе диффузии как раз и означает, что поток частиц направлен от больших значений концентрации к меньшим, то есть в направлении, противоположном производной dn/dz. Действительно, пусть n(z) — убывающая функция, то есть концентрация частиц падает с ростом z. Тогда производная dn/dz (градиент концентрации) отрицательна, а поток Ф получается положительным, то есть направлен в сторону увеличения z.
Если обе части уравнения (4.7) умножить на массу m0 диффундирующих молекул, то для потока массы М = m0Ф получим аналогичное уравнение
где r = т0n — масса диффундирующего вещества в единице объема, то есть его плотность. Связь (4.7) потока частиц с градиентом dn/dz концентрации называется первым законом Фика.
Первый закон Фика ничего не говорит о величине коэффициента диффузии, который должен в каждом конкретном случае определяться экспериментально. Поэтому этот закон носит эмпирический характер. Он применим не только для газов, но и для твердых и жидких тел. Следует отметить также, что перенос вещества в газах и жидкостях может осуществляться и механическим путем за счет конвекционных потоков (скажем, за счет ветра в атмосфере или течения в океане). Важно не путать диффузию, которая происходит из-за молекулярного движения, с конвекцией, возникающей вследствие воздействия внешних сил.
Заметим, что если система является смесью, то первый закон Фика записывается точно в такой же форме для каждого из компонентов смеси в отдельности, но коэффициенты диффузии, вообще говоря, различаются. Это значит, что в смеси, скажем, двух газов может случиться так, что концентрация частиц одного из компонентов уже выровнялась, а второго — еще нет.
Второй закон Фика позволяет найти зависимость концентрации диффундирующих частиц от времени. Для его вывода рассмотрим два параллельных друг другу одинаковых квадратика, расположенных в близких точках с координатами z и z + dz. Для определенности будем считать, что n(z) — убывающая функция (рис. 4.4).
Рис. 4.4. Иллюстрация явления диффузии (к выводу второго закона Фика)
Тогда через левую площадку за время dt входит Ф(z)dt частиц, а через правую выходит Ф(z + dz)dt частиц.
Увеличение числа частиц dN в пространстве между площадками за время dt равно разности числа входящих и выходящих частиц:
Разделив dN на объем Sdz зазора между квадратиками, получаем изменение концентрации частиц за время dt
Используя первый закон Фика, находим отсюда (здесь мы уже переходим к частным производным)
Обычно коэффициент диффузии не зависит от координат, и мы получаем уравнение, выражающее второй закон Фика:
Если ввести плотность потока частиц j = Ф/S (число частиц, пересекающих единичную площадь в единицу времени), то уравнение (4.8) можно записать в иной форме:
Это уравнение — один из примеров уравнения непрерывности, встречающегося во многих областях физики и выражающего в данном случае закон сохранения числа частиц. Его смысл: скорость изменения числа частиц в объеме равна разности потоков входящих и выходящих частиц (при условии, что внутри объема не происходит рождения или исчезновения частиц).
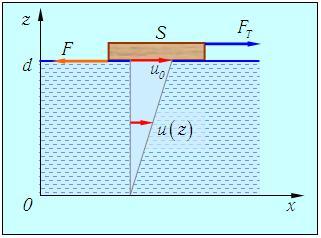
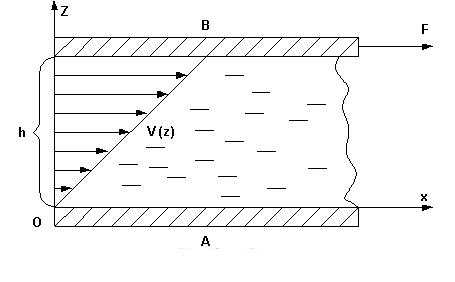
Вязкость. Рассмотрим следующий мысленный опыт. Пусть на поверхности жидкости плавает пластина, которую медленно тянут направо с силой FT (рис. 4.3).
Рис. 4.5. Сила внутреннего трения F, действующая на пластину, движущуюся со скоростью u0, по поверхности жидкости
Опыт показывает, что при установившемся движении пластина перемещается с постоянной скоростью u0. Пусть расстояние до неподвижного дна равно d, а площадь пластины равна S. Что мы можем сказать о течении жидкости?
Ясно, что кроме силы FT на пластину должно действовать что-то еще: иначе она двигалась бы равноускоренно. Это «что-то еще» может действовать только со стороны жидкости. Другими словами, на пластину со стороны жидкости действует сила F, подобная силе трения. Она направлена влево и по величине равна действующей силе FT. Каково происхождение этой силы? Прилегающий к пластине слой жидкости «прилипает» к ней и движется с той же скоростью u0. Аналогично слой жидкости, прилегающий ко дну, имеет нулевую скорость. Следовательно, в системе устанавливается некоторое распределение скоростей u(z), где z — расстояние от дна. В конечном итоге неподвижное дно через жидкость действует на пластину, порождая силу внутреннего трения, уже знакомую нам из механики жидкостей и газов.
В соответствии со сказанным, заведомо должны выполняться граничные условия u(0) = 0, u(d) = u0. Сила внутреннего трения возникает как раз вследствие этого распределения скоростей: вышележащий слой «трется» о нижележащий и тормозится им (соответственно, более быстрый слой стремится ускорить более медленный).
Опыт показывает, что сила внутреннего трения F связана со скоростью u0 соотношением (см. рис. 4.3)
Коэффициент h, имеющий размерность
называется коэффициентом динамической вязкости (внутреннего трения).
Чтобы найти распределение скоростей в этой системе, представим себе наблюдателя, находящегося на расстоянии z от дна и движущегося вместе с жидкостью со скоростью u(z). С точки зрения этого наблюдателя, его слой покоится, а пластина движется со скоростью u0 – u(z). Зависимость той же силы F от скорости должна теперь описываться аналогичной формулой с заменой
В результате получаем
Приравнивая выражения (4.11) и (4.12), находим скорость слоя как функцию расстояния от дна
Мы получили линейный закон распределения скоростей (рис. 4.6), удовлетворяющий нашим граничным условиям u(0) = 0, u(d) = u0.
Рис. 4.6 Линейное распределение скоростей в жидкости
Такое распределение скоростей связано с простотой рассмотренной системы. В других случаях течение имеет более сложный характер, но и тогда мы можем воспользоваться найденной закономерностью. Действительно, рассмотрим жидкость, в которой существует градиент скоростей по координате z. Относительная скорость слоев с координатами z и z + dz равна
Поскольку мы рассматриваем сколь угодно малые расстояния dz, то для малых площадей S течение можно считать плоским и описываемым прежними формулами. Тогда сила внутреннего трения между соседними слоями будет определяться уравнением (4.11), где вместо отношения u0/d стоит градиент скорости относительного движения слоев du/dz:
Такой закон действительно соответствует опытам по определению силы внутреннего трения между слоями жидкости или газа при ламинарном течении и был установлен Ньютоном.
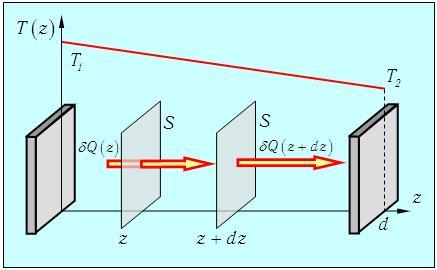
Теплопроводность. Предположим теперь, что есть два источника тепла различной температуры Т1 и Т2. Представим их себе как широкие пластины, расположенные перпендикулярно оси z в точках с координатами z = 0 и z = d. Газ, заполняющий зазор между пластинами, передает тепловую энергию от горячего тела к более холодному. При этом в газе устанавливается некоторое распределение температур T(z), удовлетворяющее граничным условиям Т(0) = T1 и T(d) = Т2 (рис. 4.).
Рис. 4.7. Распределение температуры между двумя источниками
Поместим между источниками квадратик площадью S, параллельный пластинам. Опыт показывает, что за время dt через площадь S протекает количество теплоты dQ, причем
Постоянная k называется коэффициентом теплопроводности и имеет размерность
Соотношение (4.15) называется законом Фурье.
Отрицательный знак (как и в первом законе Фика) указывает, что поток тепла направлен в сторону понижения температуры, то есть против градиента температуры dT/dz. При этих условиях в равновесном состоянии в газе установится линейный закон изменения температуры. Действительно, через квадратик единичной площади, расположенный в точке z, в единицу времени втекает количество теплоты
Через такой же квадратик в точке z + dz в единицу времени вытекает теплота
Если температура между квадратиками не меняется (установилось равновесие), то эти потоки теплоты равны между собой, то есть
Из равенства нулю второй производной следует, что функция линейна:
Из граничных условий в концевых точках находим константы интегрирования:
В сущности, мы получили аналог закона распределения скоростей при рассмотрении вязкости жидкости: достаточно заменить
Это следствие стационарности, то есть того факта, что мы рассматривали установившееся течение или распределение температур. То же следует из второго закона Фика: для стационарной системы: производная по времени в левой части уравнения (4.9) равна нулю, откуда следует равенство нулю второй производной концентрации частиц по координате z, что эквивалентно линейности функции n(z).
Пример. Определим, какое количество тепловой энергии уносится в единицу времени через окно площадью S = 2 м 2 с расстоянием между стеклами d = 5 см, если в комнате поддерживается температура t1 = 20 °С, а на улице стоит мороз:
t2 = –20 °С.
Сразу заметим, что поскольку величина градуса по шкалам Цельсия и Кельвина одинакова, то разность температур
Коэффициент теплопроводности воздуха k = 0,025 Дж/(м·с·К). Для стекла этот коэффициент в 20 раз больше, так что его наличие можно не учитывать. К тому же толщина стекла много меньше промежутка между стеклами. Поэтому от мороза нас оберегает именно воздушная прослойка между стеклами. В соответствии со сказанным, в этом промежутке устанавливается линейное распределение температуры, так что производная dT/dz постоянна и равна
Поток тепловой энергии равен тогда
Расход тепловой энергии через одно окно за месяц
Решая эту задачу, мы неявно сделали сильное предположение, что температура внутреннего стекла совпадает с температурой в комнате, а наружного — с температурой окружающего воздуха. Из практики каждый знает, что это не так: на самом деле наружная поверхность стекла несколько теплее, а внутренняя — немного холоднее. В действительности градиент температур в промежутке между рамами может быть раза в два меньше, что соответственно уменьшает поток тепловой энергии наружу. Однако точное решение задачи выходит за рамки данного курса.
Нетрудно заметить то общее, что есть у всех обсуждавшихся явлений. Во все уравнения переноса входит градиент некоторой величины — концентрации частиц, скорости течения, температуры. Во всех случаях при условии стационарности устанавливается линейное распределение этой величины. Все это потому, что явления переноса имеют общее происхождение — молекулярное движение.
Законы Фика | Основы диффузии
Итак, в основе любой теории диффузии (красителей в волокнистых материалах, компонентов в пластических массах, обмена ионов в ионообменных материалах, а также частиц в кристаллических веществах, включающих металлы, полупроводники, оксиды, керамику, стекла и т.д.), лежат законы Фика. Существуют два закона Фика – первый и второй.
Первый закон Фика
Первый закон Фика описывает квазистационарные процессы, когда проницаемая для обменивающихся местами частиц мембрана (пластинка) разделяет две среды (которые могут быть жидкими или газообразными) с существенно постоянными условиями на границах раздела. Эта мембрана может быть инертной по отношению в диффундирующим веществам (например, пористое стекло, разделяющее водные солевые растворы различной концентрации или солевого состава) или активной по отношению к одному или нескольким диффундирующим компонентам (например, палладиевая мембрана, пропускающая через себя водород при высокой температуре из-за специфических процессов сорбции на ее границе и практически не пропускающая другие газы).
Уравнение, описывающее первый закон Фика, имеет следующий вид:
где j – поток вещества через единицу поверхности, D – коэффициент диффузии (в общем случае – коэффициент взаимодиффузии), C — концентрации по толщине мембраны, равная разнице концентраций переносимого вещества по обе стороны мембраны, x — толщина мембраны.
Очевидно, что к обсуждаемым нами процессам образования цинкового покрытия это уравнение неприменимо, поскольку изучаемые нами процессы являются нестационарными.
Второй закон Фика описывает нестационарные процессы, и именно его необходимо применять для описания закономерностей, с которыми имеют дело как металлурги, так и работники других специальностей, соприкасающиеся с проблемами массопереноса в твердых телах.
Рассмотрим его действие на следующем примере. Возьмем два одинаковых образца, имеющих плоскую поверхность и состоящих из металла, который под воздействием нейтронного облучения способен создавать радиоактивные атомы той же природы. Облучим нейтронным потоком один из двух образцов с тем, чтобы создать в нем радиоактивность, соединим плотно по поверхностям облученный и необлученный образцы между собой и для убыстрения процесса будем выдерживать эту композицию при повышенной температуре. Вследствие теплового движения радиоактивные атомы из одной части образца будут диффундировать во вторую его часть, причем этот процесс будет продвинут тем более, чем более высока температура и чем больше время опыта. Затем образцы разъединим, и в каждом образце послойно измерим радиоактивность (технология этого типа эксперимента разработана очень хорошо). В результате эксперимента получаются кривые, изображенные на рис. 7.38, которые соответствующим образом обрабатываются для расчета эффективных коэффициентов диффузии. Концентрация радиоактивных ионов на межфазной границе будет равна половине той, что была в исходном левом образце, а сам процесс диффузии будет описываться уравнением:
Метод обработки таких кривых, как следует из литературы, был предложен физиком по фамилии Матано, и, как правило, называется методом Матано и иногда методом Матано- Больцмана (вероятно, из-за того, что метод возник как результат анализа решений уравнений диффузии, полученных одним из великих физиков теперь уже позапрошлого века Больцманом).
Если поверхность образца контактирует с какой-либо средой в жидкой форме, то на границе раздела концентрация данной среды, как правило, остается постоянной, но на форме фронта в железном образце эта особенность эксперимента при условии постоянства эффективного коэффициента диффузии сказывается достаточно мало (рис.7.39).
Для процесса цинкования необходимо смоделировать именно такую картинку. В этом случае концентрация диффундирующего вещества на границе двух сред является практически постоянной, и диффузия вещества в другую среду будет идти до тех пор, пока не достигнет стационара.
Рис. 7.38. Форма фронта диффузии при контакте двух твердых образцов, в одном из которых (в данном случае слева) методом нейтронного облучения созданы радиоактивные атомы, для двух значений времени эксперимента.
Рис. 7.39. Ожидаемая форма фронта в поглощающей среде при диффузии из среды с постоянной концентрацией на границе.
Второй закон Фика
Уравнение нестационарной диффузии описывается, как было уже сказано, вторым законом Фика, который для диффузии с постоянной концентрацией на границе двух фаз имеет следующий вид:
где n = 2, 1 или 0 – для шара, бесконечного цилиндра и бесконечной пластины.
Для бесконечной пластины уравнение имеет вид:
Ниже приведены соответствующие решения для степени завершения обмена как функции времени при постоянных коэффициентах диффузии:
для шара:
для пластины:
и для бесконечного цилиндра:
μ — корни функции Бесселя нулевого порядка, Bt = π 2 F0
N — степень завершения процесса обмена
F0 = D*t / l 2 — безразмерный параметр, где (D — коэффициент диффузии, t — время, l — линейный параметр)
Эти уравнения показывают, какая доля атомов (от максимально возможной) накапливается в поглощающей части образца.
Анализ показывает, что получаемые кривые, изображенные на рис. 7.39, никоим образом не напоминают типичный фронт сорбции цинка поверхностью железа, картинку которого можно видеть на рис. 7.40. Если верить кривой, полученной на рис. 7.39, наибольшей толщиной должны обладать ζ— и Г1-фазы, а δ-фаза должна иметь промежуточную толщину (о η-фазе мы поговорим несколько позже). Аналогичные результаты (то есть не совпадающие с фронтом, изображенным на рис. 7.39) были получены в значительном количестве исследований, и вот отсюда начинается игра ума.
Одни начинают искать причину в том, что поскольку изучаемое тело имеет кристаллическую структуру, то коэффициенты диффузии в различных направлениях являются различными. Действительно, на монокристаллах в ряде случаев это доказано. Но вот беда: сталь – это поликристаллическое тело, и для процесса цинкования этим вряд ли можно объяснить упомянутые выше экспериментальные закономерности.
Другие ищут причину отклонения от теоретической зависимости в методе Матано в том, что необходимо в уравнении второго закона Фика использовать не градиент концентрации, а градиент химического потенциала. В этом случае уравнение значительно усложняется, и неизвестно, какие результаты – отражающие или не отражающие действительность – будут получены.
Наконец, третьи пошли логически более правильным путем. На самом деле, при диффузии в металле с примесью (сплаве) диффундирует не один вид частиц, а, как минимум, два. Эти два вида частиц диффундируют навстречу друг другу, к тому же обладают различной подвижностью. Если отсчитывать скорость их передвижения от некоторой воображаемой плоскости (рис 7.41), то будет обнаружено, что через некоторое время эксперимента эта плоскость передвинется в сторону той части образца, которая содержит более быстрые частицы (эффект Киркендаля).
Рис. 7.40. Форма фронта, рассчитанная из содержания цинка в каждой из фаз внутри цинкового покрытия.
Рис. 7.41. Сущность эффекта Киркендаля. Пластина из латуни окружена слоем меди, нанесенной электролитически, причем на границе латунного образца предварительно закреплены метки из молибденовой проволоки. В результате выдерживания образца в течение нескольких сотен часов при повышенной температуре метки передвинулась внутрь образца.
Когда анализируют данные по кинетике образования цинк- железного покрытия на образце, исследуются дотошно любые факты, включая тип и структуру образующихся железо-цинковых сплавов, но ни в одной статье до настоящего времени не анализировалась форма фронта цинка в покрытии. Между тем, именно форма фронта говорит о многом, и именно выяснение причин ее образования может стать ключом к количественному описанию скорости образования железо-цинковых слоев.Обратим внимание на следующее. Почти во всех исследованиях в низкотемпературной области (достоверных сведений о форме фронта в высокотемпературной области нами не найдено) образуется форма обрывного фронта, близкая к изображенной на рис. 7.40. Эта форма не сильно зависит от температуры процесса, толщины образующегося покрытия и наличия или отсутствия в образце кремния (фосфора). Между тем имеется очень мало процессов, которые характеризуются такой формой фронта. Одним из таких процессов является процесс горения с быстрым отводом образующихся продуктов горения от поверхности. Для горящего шара, например, процесс горения описывается уравнением:
где R — радиус шара до начала горения, r — радиус координаты горения, D — коэффициент диффузии.
Очевидно, что если мы сделаем плоский образец с защитой боковых поверхностей, то процесс горения будет происходить только на одной из поверхностей без изменения ее реальной площади, то есть скорость уменьшения толщины образца будет пропорциональна времени. Пример такого процесса – «курение сигареты» автоматическим курильщиком с постоянной скоростью просасывания воздуха через образец.
Между тем, в огромном большинстве исследований наблюдается обратноквадратичная зависимость скорости образования слоя (скорости вымывания железа в расплав) от времени, то есть выполняется зависимость:
Однако необходимо тщательно проверить последнее утверждение, прежде чем принимать его за аксиому.
На рис. 7.42 и 7.43 приведены данные по зависимости скорости накопленияжелеза в расплаве от времени при различных температурах. В книге утверждается, что при построении этих данных в координатах получаются прямые линии для всех температур, кроме данных при 510°С, где наблюдается прямолинейная зависимость. Проверим это утверждение.
Рис. 7.42. Зависимость скорости накопления железа в расплаве с течением времени от температуры в высокотемпературной области.
Рис. 7.43. Зависимость скорости накопления железа в расплаве от времени в низкотемпературной области.
Таблица № 7.5. Определение формального порядка реакции методом сравнения с базисной зависимостью для данных по скорости вымывания железа из образца в течение процесса цинкования.
ОСНОВНЫЕ ЗАКОНЫ МАССОПЕРЕДАЧИ
В процессах массопередачи следует различать несколько случаев массообмена: между потоком газа или пара и потоком жидкости; между потоками жидкости; между потоками жидкости и твердой фазой; между потоками газа или пара и твердой фазой.
Основными законами массопередачи являются закон молекулярной диффузии (первый закон Фика), закон массоотдачи (закон Ньютона — Щукарева) и закон массопроводности.
Закон молекулярной диффузии (первый закон Фика), основанный на том, что диффузия в газах и растворах жидкостей происходит в результате хаотического движения молекул, приводящего к переносу молекул распределяемого вещества из зоны высоких концентраций в зону низких концентраций, гласит: количество вещества, перенесенного путем диффузии, пропорционально градиенту концентраций, площади, перпендикулярной направлению диффузионного потока, и продолжительности процесса:
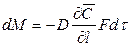
где: dM – количество вещества, перенесённого путём диффузии; D – коэффициент пропорциональности, или коэффициент диффузии; 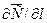
Коэффициент диффузии показывает, какое количество вещества диффундирует через поверхность в 1 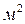
Знак «минус» в правой части уравнения показывает, что при молекулярной диффузии концентрация убывает.
Если единицы измерений [М] = [кг], [Р] = [ 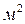
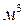
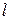
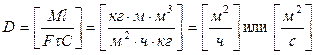
Значения коэффициента диффузии обычно берут из справочников или находят по следующим формулам:
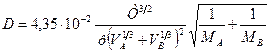
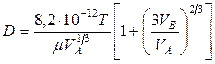
где: Т – температура, К; 
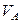
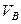
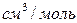

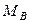
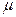
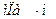
Коэффициенты диффузии зависят от агрегатного состояния систем. Для газов коэффициенты диффузии имеют значения (0,1. 1,0)10 -4 
Коэффициенты диффузии в газах почти не зависят от концентрации, в то время как коэффициенты диффузии в жидкостях изменяются с изменением концентрации диффундирующего вещества.
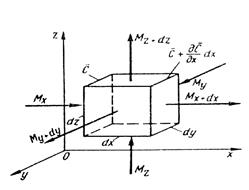
Дифференциальное уравнение молекулярной диффузии (второй закон Фика) получают, рассмотрев материальный баланс по распределяемому веществу для элементарного параллелепипеда, выделенного мысленно в потоке одной из фаз (рис. 12.3).
Рис. 12.3. К выводу дифференциального уравнения молекулярной диффузии
Пусть через этот элементарный параллелепипед за счет молекулярной диффузии перемещается вещество. Если через грани 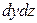
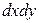
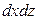
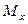
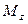


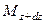

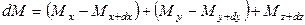
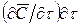
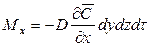
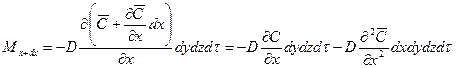

Аналогично найдем разности между количествами вещества, прошедшего через другие противоположные грани параллелепипеда.
Общее количество приобретенного вещества

Это же количество вещества можно найти умножением объема параллелепипеда на изменение концентрации диффундирующего вещества за время 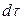

Приравнивая уравнения (12.12) и (12.13), получим дифференциальное уравнение молекулярной диффузии
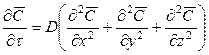
Основной закон массоотдачи, который является аналогом закона Ньютона, был установлен русским ученым Щукаревым при изучении растворения твердых тел. Этот закон формулируется так: количество вещества, перенесенного потоком от поверхности раздела фаз (контакта фаз) в воспринимающую фазу или в обратном направлении, прямо пропорционально разности концентраций у поверхности контакта фаз и в ядре потока воспринимающей фазы, площади поверхности контакта фаз и продолжительности процесса.
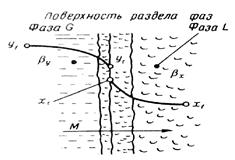
Согласно теории диффузионного пограничного слоя распределяемое вещество переносится из ядра потока жидкости к поверхности раздела фаз непосредственно конвективными потоками жидкости и молекулярной диффузией. В рассматриваемой системе (рис. 12.4) различают ядро потока и приграничный диффузионный слой. В ядре перенос вещества осуществляется преимущественно потоками жидкости или газа. В условиях турбулентного течения потоков концентрация распределяемого вещества в данном сечении в условиях стационарного режима сохраняется постоянной. По мере приближения к пограничному диффузионному слою турбулентный перенос снижается и начинает увеличиваться перенос за счет молекулярной диффузии. При этом появляется градиент концентрации распределяемого вещества, растущий по мере приближения к границе. Таким образом, область пограничного диффузионного слоя — это область появления и роста градиента концентрации, область увеличения влияния скорости молекулярной диффузии на общую скорость массопередачи.
Рис.12.4. К выводу уравнения массоотдачи
Примем, что распределяемое вещество М переходит из фазы G, в которой его концентрация выше равновесной, в фазу L.
Если концентрации вещества в ядрах фаз принять равными 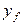
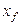
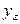

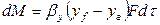
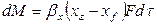
где: 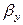
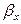
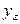



Размерность коэффициента массоотдачи 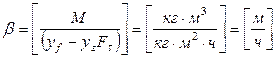
Коэффициент массоотдачи показывает, какое количество вещества передается от поверхности контакта фаз площадью в 1 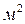
По физическому смыслу коэффициенты массоотдачи отличаются от коэффициентов массопередачи, но выражаются в одинаковых единицах.
Для установившегося процесса 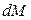
Для этого случая уравнение (12.15) перепишется так:
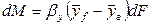
Если 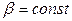
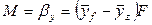
Если рассмотреть вновь элементарный объем фазы (см. рис. 12.3), перемещающийся в пограничном слое, то можно утверждать, что концентрация распределяемого вещества в нем меняется не только за счет молекулярной диффузии, но также и за счет турбулентного переноса его. В этом случае концентрация распределяемого вещества будет функцией не только координат и времени, как в случае только молекулярной диффузии, но и скорости перемещения.
Соответственно этому изменение концентрации G выразим через субстанциональную производную:
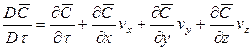
В этом уравнении сумма членов 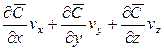
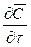
Увеличение количества распределяемого вещества за счет молекулярной диффузии определяется уравнением (12.14). Приравнивая уравнение (12.17) к (12.14) и заменяя локальное изменение концентрации 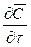
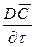
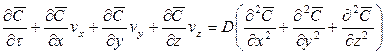
Для полного математического описания процесса это уравнение должно быть дополнено уравнением, характеризующим условие на границе раздела фаз.
Количество вещества, передаваемого из фазы в фазу у границы, определяется основным законом конвективной диффузии (12.15). У поверхности раздела фаз вещество переходит из фазы в фазу, как было установлено выше, за счет молекулярной диффузии [см. уравнение (12.9)]. Приравнивая эти уравнения, получим
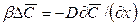
где: 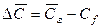
Уравнение (12.19) характеризует условие массообмена на границе фазы и дополняет уравнение (12.18), являясь вместе с ним математическим описанием процесса конвективной диффузии.
Критериальные уравнения конвективной диффузии получают из уравнений (12.18) и (12.19).
Для получения диффузионных критериев, подобия воспользуемся методами теории подобия. Из уравнения (12.19) получим безразмерный комплекс 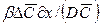
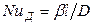
который характеризует условия на границе рассматриваемой фазы, т. е. выражает отношение интенсивности переноса вещества в ядре фазы конвективной диффузией 
Из дифференциального уравнения конвективной диффузии (12.18), разделив все члены на 
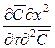
и соответственно диффузионный критерий Фурье
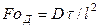
и диффузионный критерий Пекле
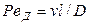
Критерий 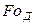
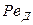

Диффузионный критерий Прандтля 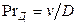
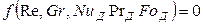
Критерий Нуссельта в этом уравнении является определяемым в отличие от других критериев, которые являются определяющими, т. е. составленными целиком из параметров, входящих в условие однозначности. Коэффициент массоотдачи, входящий в критерий Нуссельта, не входит в условие однозначности и является искомой величиной.
В явном виде уравнение (12.23) перепишется так:
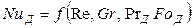
Критерий Грасгофа в этом уравнении характеризует конвективную диффузию в условиях естественной конвекции.
В случае стационарных процессов из общего критериального уравнения исключается критерий Фурье и оно приобретает вид
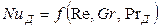
При вынужденном движении можно пренебречь естественной конвекцией. В этом случае из уравнения (12.25) выпадает критерий Грасгофа и уравнение приобретает вид

Конкретные критериальные уравнения приводятся в соответствующих главах этой части.
По значениям критерия Нуссельта, найденным по критериальным уравнениям, определяют коэффициент массоотдачи

Между переносом теплоты, массы и механической энергии существует, как отмечалось ранее, аналогия, эти процессы описываются однотипными дифференциальными уравнениями.
При рассмотрении движения потока жидкости в трубе различают пограничный слой и ядро потока. В ядре турбулентного потока происходит выравнивание скоростей по нормали к вектору скорости, в пограничном же слое происходит резкое изменение скорости потока до нуля. Такое же выравнивание температур и концентраций происходит в процессах тепло- и массопередачи. Таким образом, имеет место аналогия между этими процессами.
Исходя из этой аналогии, можно приближенно определять коэффициенты массоотдачи по данным о трении жидкостного потока или о скорости переноса теплоты.
На основании гидродинамической аналогии можно определить отношение коэффициента массоотдачи 
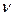

Критерий Стантона характеризует подобие полей концентраций и скоростей при массоотдаче в турбулентных потоках.
Существует связь между коэффициентом массопередачи и коэффициентами массоотдачи. Рассмотрим процесс массопередачи при переходе распределяемого вещества из фазы G в фазу L при условии линейных зависимостей между рабочими и равновесными концентрациями (см. рис. 12.4). Примем, что на границе раздела фаз достигается равновесие.
Количество вещества, перемещающегося из фазы G к поверхности на границе раздела фаз, может быть определено по уравнению
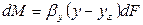
где: 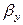
Количество распределяемого вещества, перемещающегося от элемента поверхности в фазу L, может быть вычислено также по фазе L по уравнению (12.15). В этом случае движущую силу следует выразить разностью 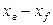
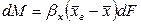
где: 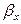
Так как известна равновесная зависимость 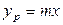
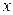
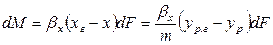
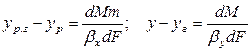
Сложим левые и правые части этих уравнений
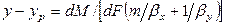
так как 
Из основного уравнения массопередачи (12.4) получим
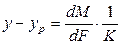
Приравнивая правые части уравнения, получим
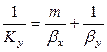
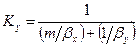
Рассуждая аналогично, для фазы L будем иметь
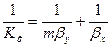
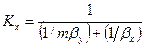
Левые части этих уравнений представляют собой общее диффузионное сопротивление переносу, а их правые части — сумму диффузионных сопротивлений массоотдаче в фазах. Зависимости (12.28) и (12.29) являются поэтому уравнениями аддитивности фазовых сопротивлений.
Коэффициенты 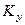
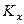
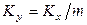
Дата добавления: 2015-03-14 ; просмотров: 4869 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://ecm-zink.ru/info/stati/zakonyi-fika-osnovyi-diffuzii.html
http://helpiks.org/2-105082.html