Уравнение перпендикуляра к двум прямым онлайн

Уравнение перпендикулярной прямой

Альтернативная формула
Прямая, проходящая через точку M₁(x₁; y₁) и перпендикулярная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения перпендикулярной прямой (см. также как составить уравнение параллельной прямой).

Пример №1 . Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3 .
Решение. Данную прямую можно представить уравнением y = 4 /₉x – 1 /₃ (a = 4 /₉). Уравнение искомой прямой есть y+1 = -9/4(x-2) , т.е. 9x+4y-14=0 .

Пример №2 . Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0 , т.е. 9x+4y-14=0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0 .
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0 . Формула (1) неприменима, так как a=0 .

Вычисление расстояния между двумя прямыми и координат концов общего перпендикуляра.

Координаты концов общего перпендикуляра к двум скрещивающимся или пересекающимся прямым.

В пространстве даны четыре точки:

Прямые AB и CS являются скрещивающимися или пересекающимися.
Найти координаты концов общего перпендикуляра к прямым AB и CS

Пусть выполняются пять условий:

1. Точка M(xm, ym, zm) принадлежит прямой AB ;
2. Точка N(xn, yn, z6) принадлежит прямой CS ;
3. Прямая MN перпендикулярна прямой AB ;
4. Прямая MN перпендикулярна прямой СS ;
5. Прямые AB и СS не являются параллельными;

Тогда отрезок [MN] является общим перпендикуляром к прямым AB и CS, а длина отрезка [MN] является кратчайшим расстоянием между прямыми AB и CS.

Выполняются пять следующие пять условий:

Координаты параллельных (коллинеарных) векторов пропорциональны.

Скалярное произведение перпендикулярных (ортогональных) векторов равно нулю.

Векторное произведение неколлинеарных векторов не равно нулевому вектору. Модуль векторного произведения неколлинеарных векторов строго больше нуля.

По условию, так как прямые AB и CS не параллельны, векторное произведение векторов

Выполняются следующие пять условий:

Выражаем из первых двух уравнений xm, ym, zm, xn, yn, zn

Находим координаты вектора MN

Подставляя xm, ym, zm, xn, yn, zn в третье и четвёртое уравнение, найдём m и n:

Получаем систему двух уравнений с двумя неизвестными m, n:

Имеем следующую систему из двух уравнений с двумя неизвестными m, n:

Так как квадрат скалярного произведения неколлинеарных векторов всегда строго меньше произведения квадратов модулей этих векторов, главный определитель этой системы:

Поэтому данная система имеет единственное решение.

Координаты концов общего перпендикуляра [MN] к двум скрещивающимся прямым. Отрезок [MN] перпендикулярен AB и перпендикулярен SC

Координаты точки M(xm, ym, zm), лежащей на прямой AB:

Координаты точки N(xn, yn, zn), лежащей на прямой SC:

Координаты концов общего перпендикуляра к скрещивающимся (или пересекающимся) прямым AB и CS:

Расстояние между непараллельными прямыми.

Два способа вычисления расстояния между непараллельными прямыми.

Расстояние между непараллельными прямыми AB и SC может быть найдено по формуле:

Расстояние между непараллельными прямыми AB и SC может быть найдено вторым способом, как высота параллелепипеда, сторонами основания которого являются [AB] и [SC], а боковым ребром является [AS].

Перенеся начало вектора SC в точку A, построим параллелепипед на векторах AB, SC, AS, объём которого равен модулю смешанного произведения векторов AB, SC, AS, а площадь основания равна модулю векторного произведения векторов AB и SC. Расстояние между прямыми AB и SC равно высоте этого параллелепипеда, построенного на векторах AB, SC, AS:

Векторное произведение векторов AB и SC имеет координаты:

Модуль векторного произведения векторов AB и SC:

Модуль смешанного произведения векторов AS, AB, SC:

Кратчайшее расстояние между прямыми AB и CS может быть найдено по формуле:

Расстояние между параллельными прямыми AB и CS

Расстояние между параллельными прямыми AB и CS равно расстоянию от точки S(xs, ys, zs) до прямой AB.

Существуют также два способа нахождения расстояния между двумя параллельными прямыми, то есть два способа нахождения расстояния от точки до прямой. Сначала найдём координаты проекции точки на прямую. Прямая AB задана координатами двух её точек

Точка K является проекцией точки S на прямую AB.

Найти координаты точки K

Для нахождения координат точки K используем условия:

1. Векторы AK и AB – коллинеарны, их координаты пропорциональны;
2. Векторы SK и AB ортогональны, и их скалярное произведение равно нулю ;

Из первого уравнения

Подставляя xk, yk, zk во второе уравнение, находим t:

Координаты проекции точки S на прямую AB, то есть координаты точки K(xk, yk, zk):

Расстояние между точкой S и прямой AB может быть найдено по формуле:

Расстояние между точкой S и прямой AB может быть найдено вторым способом, как высота параллелограмма, сторонами которого являются [AB] и [AS].

Векторное произведение векторов AB и AS имеет координаты:

Модуль векторного произведения векторов AB и AS:

Модуль вектора AB:

Расстояние между точкой S и прямой AB может быть найдено по формуле:

Программа «Вычисление расстояния между двумя прямыми и координат концов общего перпендикуляра».

Выдаётся точное значение координат координат концов общего перпендикуляра к прямым AB и CS виде несократимой рациональной дроби c/r.
Выдаётся точное значение расстояния между двумя прямыми в виде c*sqrt(p)/r

Дробь c/r является несократимой рациональной дробью, а подкоренное выражение p не содержит в качестве своих делителей квадраты натуральных чисел.

Результат можно вывести в файл.

Для перевода курсора в следующее поле и вычисления результата используйте клавишу Enter.

Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой

В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой

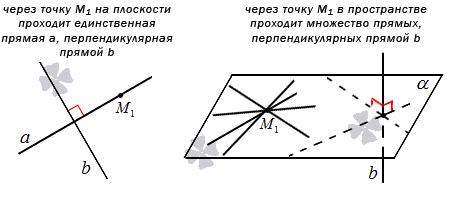
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.

Если плоскость α проходит через заданную точку М 1 перпендикулярно к заданной прямой b , то прямые, лежащие в этой плоскости, в том числе и проходящая через М 1 являются перпендикулярными заданной прямой b .

Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.

Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Если на плоскости с системой координат О х у z имеем прямую b , то ей соответствует уравнение прямой на плоскости, задается точка с координатами M 1 ( x 1 , y 1 ) , а необходимо составить уравнение прямой a , которая проходит через точку М 1 , причем перпендикулярно прямой b .

По условию имеем координаты точки М 1 . Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a , или координаты нормального вектора прямой a , или угловой коэффициент прямой a .

Необходимо получить данные из заданного уравнения прямой b . По условию прямые a и b перпендикулярные, значит, направляющий вектор прямой b считается нормальным вектором прямой a . Отсюда получим, что угловые коэффициенты обозначаются как k b и k a . Они связаны при помощи соотношения k b · k a = — 1 .

Получили, что направляющий вектор прямой b имеет вид b → = ( b x , b y ) , отсюда нормальный вектор — n a → = ( A 2 , B 2 ) , где значения A 2 = b x , B 2 = b y . Тогда запишем общее уравнение прямой, проходящее через точку с координатами M 1 ( x 1 , y 1 ) , имеющее нормальный вектор n a → = ( A 2 , B 2 ) , имеющее вид A 2 · ( x — x 1 ) + B 2 · ( y — y 1 ) = 0 .

Нормальный вектор прямой b определен и имеет вид n b → = ( A 1 , B 1 ) , тогда направляющий вектор прямой a является вектором a → = ( a x , a y ) , где значения a x = A 1 , a y = B 1 . Значит осталось составить каноническое или параметрическое уравнение прямой a , проходящее через точку с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) , имеющее вид x — x 1 a x = y — y 1 a y или x = x 1 + a x · λ y = y 1 + a y · λ соответственно.

После нахождения углового коэффициента k b прямой b можно высчитать угловой коэффициент прямой a . Он будет равен — 1 k b . Отсюда следует, что можно записать уравнение прямой a , проходящей через M 1 ( x 1 , y 1 ) с угловым коэффициентом — 1 k b в виде y — y 1 = — 1 k b · ( x — x 1 ) .

Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.

Решение примеров

Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.

Записать уравнение прямой а, которая проходит через точку с координатами M 1 ( 7 , — 9 ) и перпендикулярна прямой b , которое задано каноническим уравнением прямой x — 2 3 = y + 4 1 .

Из условия имеем, что b → = ( 3 , 1 ) является направляющим вектором прямой x — 2 3 = y + 4 1 . Координаты вектора b → = 3 , 1 являются координатами нормального вектора прямой a , так как прямые a и b взаимно перпендикулярны. Значит, получаем n a → = ( 3 , 1 ) . Теперь необходимо записать уравнение прямой, проходящее через точку M 1 ( 7 , — 9 ) , имеющее нормальный вектор с координатами n a → = ( 3 , 1 ) .

Получим уравнение вида: 3 · ( x — 7 ) + 1 · ( y — ( — 9 ) ) = 0 ⇔ 3 x + y — 12 = 0

Полученное уравнение является искомым.

Ответ: 3 x + y — 12 = 0 .

Составить уравнение прямой, которая проходит через начало координат системы координат О х у z , перпендикулярно прямой 2 x — y + 1 = 0 .

Имеем, что n b → = ( 2 , — 1 ) является нормальным вектором заданной прямой. Отсюда a → = ( 2 , — 1 ) — координаты искомого направляющего вектора прямой.

Зафиксируем уравнение прямой, проходящую через начало координат с направляющим вектором a → = ( 2 , — 1 ) . Получим, что x — 0 2 = y + 0 — 1 ⇔ x 2 = y — 1 . Полученное выражение является уравнение прямой, проходящей через начало координат перпендикулярно прямой 2 x — y + 1 = 0 .

Ответ: x 2 = y — 1 .

Записать уравнение прямой, проходящей через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 .

Из уравнения y = — 5 2 x + 6 угловой коэффициент имеет значение — 5 2 . Угловой коэффициент прямой, которая перпендикулярна ей имеет значение — 1 — 5 2 = 2 5 . Отсюда делаем вывод, что прямая, проходящая через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 , равна y — ( — 3 ) = 2 5 · x — 5 ⇔ y = 2 5 x — 5 .