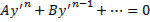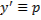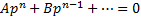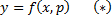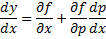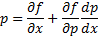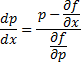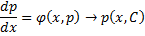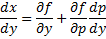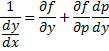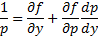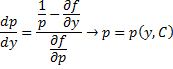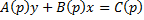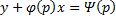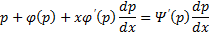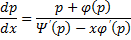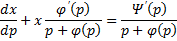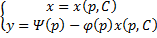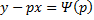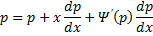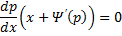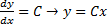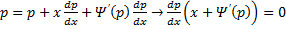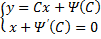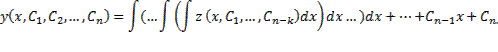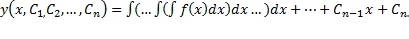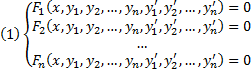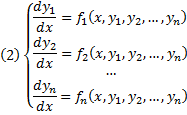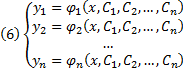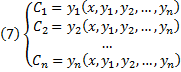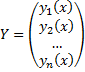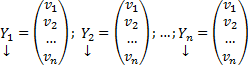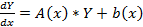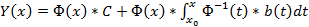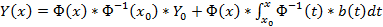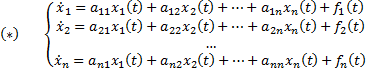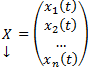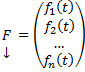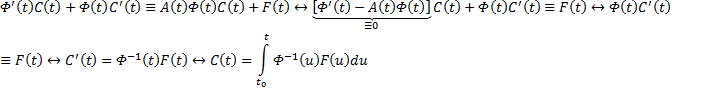Уравнение первого порядка n ой степени

Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.

Уравнения, не разрешённые относительно производной, выглядят так: .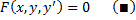

Уравнения первого порядка n-ой степени решаются так:

Если из уравнения y можно выразить, то есть , то это решается методом введения параметра, а именно: Обозначим , получим:

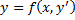
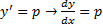
Продифференцируем по x:

Получили уравнение, разрешённое относительно производной. p(x,C) подставляем в (*), получим: 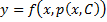. Это и будет решение.

Рассмотрим теперь случай, когда из уравнения можно явно выразить x, то есть . Вводим параметр , получаем . Дифференцируем по y обе части:

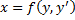
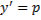
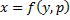
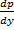
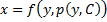
Мы получили уравнение, разрешённое относительно производной . В итоге получаем: .

Уравнение Лагранжа – это уравнение, линейное относительно x и y, оно имеет вид: 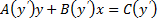. Уравнения Лагранжа ВСЕГДА интегрируется в квадратурах.

Принцип решения: Вводим параметр 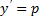, получаем:

Пусть 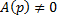, поделим всё выражение на A(p):

Продифференцируем по x:

Получили линейное уравнение первого порядка. Отсюда находим .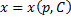

В итоге решение в параметрическом виде:

Отдельно рассмотрим случай, когда :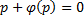

Если это тождество, то есть 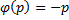, то:

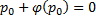
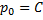
Если это не тождество, а уравнение с корнями: например, p0 – корень, то есть , тогда – решение.

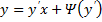
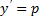
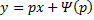
Частный случай уравнения Лагранжа – это уравнение Клеро. Это когда уравнение Лагранжа имеет следующий вид: . Принцип решения: Вводим параметр , получаем . Дифференцируем по x, получаем:

Общее решение уравнения Клеро:

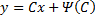
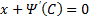
Здесь – семейство всевозможных кривых; – огибающая этого семейства, тоже является решением и называется особое решение.

Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (ФСР) однородного уравнения, общее решение неоднородного уравнения.

Простейшие ОДУ высших порядков, интегрируемые в квадратурах и допускающие понижение порядка.

Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида F (x, y(x), y ‘(x), y »(x), … , y(n)(x)) = 0, где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число n называется порядком уравнения.

Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество. Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме: y(n) = f(x, y, y ‘, y », … , y(n − 1)).

Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия. Чтобы выделить единственное решение уравнения n–го порядка обычно задают n начальных условий y(x0) = y0, y ‘(x0) = y1, y »(x0) = y2, … , y(n − 1)(x0) = yn − 1.

Общим решением дифференциального уравнения F(x, y(x), y ‘(x), y »(x), … , y(n )(x)) = 0 называется функция y = Ф(x, С1, С2, … , Сn), содержащая некоторые постоянные (параметры) С1, С2, … , Сn, и обладающая следующими свойствами:

Ф(x, С1, С2, … , Сn) является решением уравнения при любых допустимых значениях С1, С2, … , Сm;

для любых начальных данных y(x0) = y0, y ‘(x0) = y1, y »(x0) = y2, … , y(n − 1)(x0) = yn − 1, для которых задача Коши имеет единственное решение, существуют значения постоянных С1 = A1, С2 = A2, … , Сn = An, такие что решение y = Ф(x, A1, A2, …, An) удовлетворяет заданным начальным условиям.

Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С1, С2, . Сn) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

Если задачу об отыскании всех решений дифференциального уравнения удается свести к алгебраическим операциям и к вычислению конечного числа интегралов и производных от известных функций, то уравнение называется интегрируемым в квадратурах. Класс таких уравнений относительно узок.

Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ‘. y(n) ) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка.

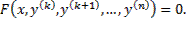
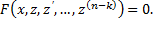
К уравнениям, допускающим понижение порядка, относятся в частности, уравнения, не содержащие искомой функции и ее производных до некоторого порядка, , т.е. уравнения вида Заменой z(x) = y(k)(x) такое уравнение сводится к уравнению (n−k)–го порядка: Если z = z(x,C1. Cn-k) решение этого уравнения, то общее решение уравнения n–го порядка может быть вычислено по формуле

Простейшее уравнение, допускающее понижение порядка — уравнение вида y(n) = f (x), его общее решение имеет вид

К уравнениям, допускающим понижение порядка, относятся уравнения, не содержащие независимой переменной — уравнения вида F(y, y’, . y(n)) = 0. Порядок уравнения можно понизить заменив y ‘ = p(y). После подстановки получим дифференциальное уравнение относительно функции p = p(y) , в котором порядок старшей производной от p(y) будет на единицу меньше, чем порядок старшей производной от y(x) в исходном уравнении.

К уравнениям, допускающим понижение порядка, относятся уравнения, не содержащие искомой функции — уравнения вида F(x, y’, . y(n)) = 0. Порядок уравнения можно понизить заменив y ‘ = p(x). После подстановки получим дифференциальное уравнение относительно функции p = p(x) на единицу меньшего порядка, чем исходное уравнение: F(x, p, p’, . p(n — 1)) = 0. Если правая часть уравнения F(x, y, y ‘. y(n) ) = 0, удовлетворяет условию однородностиF(x, ty, ty ‘. ty(n) ) = tk F(x, y, y ‘. y(n) ) то говорят, что это уравнение, однородное относительно неизвестной функции и всех ее производных. Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ‘. y(n) ) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка.

К уравнениям, допускающим понижение порядка, относятся уравнения, однородные относительно неизвестной функции и всех ее производных. Порядок такого уравнения можно понизить заменой

Выражение для первой производной от y(x) не содержит производной от z(x):

.

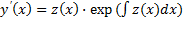
Поэтому, заменив в исходном уравнении y, y ‘. y(n) их выражениями через z(x), получим относительно z(x) дифференциальное уравнение на единицу меньшего порядка.

Основные понятия, относящиеся к системам ОДУ: порядок системы, нормальная форма системы, общее и частное решения, общий и первый интегралы. Задача Коши для нормальной системы, её геометрический смысл.

Совокупность соотношений вида:

Где y1, y2, …, yn искомые функции от независимой переменной x, называется системой обыкновенных дифференциальных уравнений первого порядка.

Будем предполагать функции F2, F2, …, Fn такими, что система разрешима относительно производных от искомых функций:

Такие системы называются нормальными системами дифференциальных уравнений.

Число уравнений, входящих в систему, называется порядком этой системы. Значит, наша система имеет n-ый порядок.

Такая система, когда в левой части уравнений стоят производные первого порядка, а правые части не содержат производных, называется нормальной.

Семейство решений системы (2), зависящее от n произвольных постоянных C1, C2, …, Cn

называют обычно общим решением этой системы.

Дадим определение общего решения системы (2) в области D изменения переменных x, y1, y2, …, yn.

В качестве области D будем рассматривать область в пространстве (x, y1, y2, …, yn), в каждой точке которой имеет место существование и единственность решения задачи Коши для системы (2).

Совокупность n функций (6), определённых в некоторой области изменения переменных x, C1, C2, …, Cn, имеющих непрерывные частные производные по x, будем называть общим решением системы (2) в области D, если система (6) разрешима относительно произвольных постоянных C1, C2, …, Cn в области D, так что при любых значениях x, y1, y2, …, yn, принадлежащих области D, системой (6) определяются значения C1, C2, …, Cn:

и если совокупность n функций (6) является решением системы (2) при всех значениях произвольных постоянных C1, C2, …, Cn, доставляемых формулами (7), когда точка (x, y1, y2, …, yn) пробегает область D.

Решение, получающееся из формулы общего решения при частных числовых значениях произвольных постоянных C1, C2, …, Cn,, включая бесконечности, будет частным решением.

Решая задачу Коши при помощи формулы общего решения всегда получаем частное решение.

1-ое определение интеграла системы. Функция φ(x, y1, y2, …, yn), не приводящаяся к постоянной, называется интегралом системы (2), если при замене y1, …, yn любым частным решением этой системы она обращается в постоянную.

2-ое определение интеграла системы. Функция φ(x, y1, y2, …, yn), имеющая непрерывные частные производные по x, y2, …, yn, и такая, что в рассматриваемой области 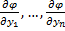не обращаются одновременно в нуль, называется интегралом системы (2), если полный дифференциал этой функции обращается тождественно в нуль в силу системы (2), то есть имеет место тождество:

.

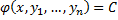
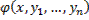
Равенство , где – интеграл системы (2) в смысле первого или второго определения, а C – произвольная постоянная, называется первым интегралом системы (2). Например, каждое из равенств (7) является первым интегралом системы (2).

Совокупность n первых интегралов (7) обладает тем свойством, что она разрешима относительно искомых функций y1, y2, …, yn, причём в результате этого мы получаем общее решение (6) системы (2) в области D. Всякую совокупность n первых интегралов, обладающую таким свойством, будем называть общим интегралом системы (2) в области D.

Фундаментальные системы решений нормальной системы однородных линейных ОДУ. Теорема существования фундаментальных систем. Теорема об общем решении (о структуре общего решения) нормальной системы однородных линейных ОДУ.

Система обыкновенных дифференциальных уравнений вида:

называется линейной системой. При система становится однородной. В векторно-матричной форме: , где
,

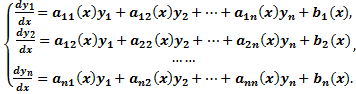
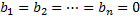
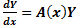
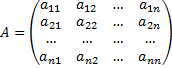
Будем искать решение . Ищем решение системы в таком виде:

Фундаментальной системой решений системы уравнений (*) называется системы из n линейно независимых вектор-функций.

Теорема о структуре общего решения линейного однородного дифференциального уравнения. Общее решение y(x) линейного однородного дифференциального уравнения есть линейная комбинация функций из фундаментальной системы решений этого уравнения: .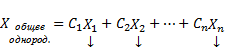

Теорема об общем решении (о структуре общего решения) нормальной системы неоднородных линейных ОДУ.

Рассмотрим неоднородную линейную систему обыкновенных дифференциальных уравнений n-го порядка

Здесь A

Справедлива следующая теорема о структуре общего решения этой неоднородной линейной системы ОДУ.

Если матрица A(x) и вектор-функция b(x) непрерывны на [a, b], и пусть Φ(x) — фундаментальная матрица решений однородной линейной системы 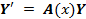, то общее решение неоднородной системы Y’ = A(x)Y + b(x) имеет вид:

где C — произвольный постоянный вектор-столбец, x0 — произвольная фиксированная точка из отрезка [a, b].

Из приведенной формулы легко получить формулу решения задачи Коши для линейной неоднородной системы ОДУ — формулу Коши.

Решением задачи Коши 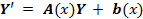, Y(x0) = Y0 является вектор-функция

Метод вариации произвольных постоянных для отыскания частных решений нормальной системы неоднородных линейных ОДУ.

Определение системы неоднородных линейных ОДУ. Система ОДУ вида:

называется линейной неоднородной. Пусть

Система (*) в векторно-матричном виде: . — система однородная, иначе – неоднородная.

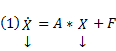
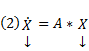
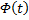
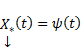
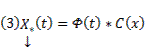
Сам метод. Пусть имеется линейная неоднородная система , тогда — линейная однородная система, соответствующая линейной неоднородной. Пусть – фундаментальная матрица системы решений, , где C – произвольный постоянный вектор, — общее решение системы. Станем искать решение системы (1) в виде , где C(x) – неизвестная (пока) вектор-функция. Хотим, чтобы вектор-функция (3) была решением системы (1). Тогда должно быть справедливо тождество:

(произвольный постоянный вектор, который получается в результате интегрирования, можно считать равным 0). Здесь точки x0, – любые.

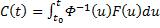
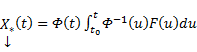
Видим, таким образом, что если в (3) в качестве C(t) брать , то вектор-функция будет решением системы (1).

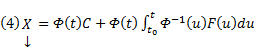
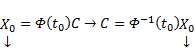
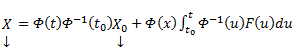
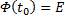
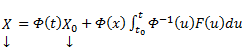
Общее решение линейной неоднородной системы (1) может быть записано в виде . Пусть требуется найти решение системы (1), удовлетворяющее начальному условию . Подстановка (4) начальных данных (5) даёт . Следовательно, решение задачи Коши (1)-(5) может быть записано в виде: . В частном случае, когда , последняя формула принимает вид: .

Дифференциальные уравнения 1-го порядка,
не разрешенные относительно производной

Уравнения 1-го порядка n-ой степени относительно производной

Пусть имеем дифференциальное уравнение

Решаем это уравнение относительно . Пусть

— вещественные решения уравнения (1).

Общий интеграл уравнения (1) выразится совокупностью интегралов:

где есть интеграл уравнения .

Таким образом, через каждую точку области, в которой принимает вещественные значения, проходит интегральных линий.

Пример 1. Решить уравнение .

Решение. Разрешим это уравнение относительно :

Пример 2. Решить уравнение .

Решение. Разрешим уравнение относительно переменной :

Положим , где — параметр; тогда получим Дифференцируя, найдем . Но так как , то будем иметь

Рассмотрим два случая:

1) , откуда , где — произвольная постоянная. Подставляя значение , получаем общее решение данного уравнения:

В равенстве нельзя заменить на и интегрировать полученное уравнение (так как при этом появится вторая произвольная постоянная, чего не может быть, поскольку рассматриваемое дифференциальное уравнение является уравнением первого порядка).

2) , откуда . Подставляя, получим еще одно решение .

Проверим, нарушится ли свойство единственности в каждой точке решения , т.е. является ли оно особым (см. часть 1.11). Для этого возьмем на интегральной кривой произвольную точку , где . Будем теперь искать решение, которое содержится в общем решении и график которого проходит через точку . Подставляя координаты этой точки в общее решение , будем иметь

откуда . Это значение постоянной подставим в . Тогда получим частное решение

которое не совпадает с решением . Для этих решений имеем соответственно . При обе производные совпадают. Следовательно, в точке нарушается свойство единственности, т. е. через эту точку проходят две интегральные кривые с одной и той же касательной. Так как произвольно, то единственность нарушается в каждой точке решения , а это означает, что оно является особым.

2°. Уравнения вида f(y,y’)=0 и f(x,y’)=0

Если уравнения и легко разрешимы относительно , то, разрешая их, получим уравнения с разделяющимися переменными. Рассмотрим случаи, когда эти уравнения не разрешимы относительно .

А. Уравнение вида разрешимо относительно :

Полагаем , тогда . Дифференцируя это уравнение и заменяя на , получим

Получаем общее решение уравнения в параметрической форме

Пример 3. Решить уравнение , где — постоянные.

Решение. Положим , тогда , или . Отсюда и .

Общим решением будет .

Б. Если уравнение вида неразрешимо (или трудно разрешимо) как относительно , так и относительно , но допускает выражение и через некоторый параметр :

то поступаем следующим образом. Имеем . С другой стороны, , так что и ; отсюда

Таким образом, получаем общее решение данного дифференциального уравнения в параметрической форме

Пример 4. Решить уравнение .

Решение. Полагаем , тогда имеем

Отсюда , общее решение .

В. Уравнение вида . Пусть это уравнение разрешимо относительно , то есть .

Полагая , получим . Но и, следовательно, , так что

Таким образом — общее решение уравнения в параметрической форме ( — параметр).

Замечание. В формулах нельзя рассматривать как производную. В них является просто параметром.

Пример 5. Решить уравнение .

Решение. Положим , тогда

Итак, — общее решение.

Аналогично случаю Б можно пытаться решать уравнение методом введения параметра .

3°. Уравнения Лагранжа

Уравнение Лагранжа имеет вид

Полагая , дифференцируя по и заменяя на , приводим это уравнение к линейному относительно как функции . Находя решение этого последнего уравнения , получаем общее решение исходного уравнения в параметрической форме:

Кроме того, уравнение Лагранжа может иметь еще особые решения вида , где — корень уравнения .

Пример 6. Проинтегрировать уравнение .

Решение. Полагаем , тогда . Дифференцируя, находим

Получили уравнение первого порядка, линейное относительно ; решая его, находим

Подставляя найденное значение в выражение для , получим окончательно

Уравнения Клеро

Уравнение Клеро имеет вид .

Метод решения тот же, что и для уравнения Лагранжа. Общее решение уравнения Клеро имеет вид

Уравнение Клеро может иметь еще особое решение, которое получается исключением из уравнений .

Пример 7. Проинтегрировать уравнение .

Решение. Полагая , получаем . Дифференцируя последнее уравнение и заменяя на , найдем

Приравнивая нулю первый множитель, получаем , откуда и общее решение исходного уравнения есть , однопараметрическое семейство прямых. Приравнивая нулю второй множитель, будем иметь . Исключая из этого уравнения и из уравнения , получим — это тоже решение нашего уравнения (особое решение).

С геометрической точки зрения кривая есть огибающая семейства прямых, даваемых общим решением (рис. 14).

Виды дифференциальных уравнений

Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.

В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.

Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.

Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.

Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».

Начнем ознакомление с темой мы с видов обыкновенных дифференциальных уравнений 1 -го порядка. Эти уравнения могут быть разрешены относительно производной. Затем перейдем в ОДУ 2 -го и высших порядков. Также мы уделим внимание системам дифференциальных уравнений.

Напомним, что y ‘ = d x d y , если y является функцией аргумента x .

Дифференциальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )

Начнем с примеров таких уравнений.

y ‘ = 0 , y ‘ = x + e x — 1 , y ‘ = 2 x x 2 — 7 3

Оптимальным для решения дифференциальных уравнений f ( x ) · y ‘ = g ( x ) является метод деления обеих частей на f ( x ) . Решение относительно производной позволяет нам прийти к уравнению вида y ‘ = g ( x ) f ( x ) . Оно является эквивалентом исходного уравнения при f ( x ) ≠ 0 .

Приведем примеры подобных дифференциальных уравнений:

e x · y ‘ = 2 x + 1 , ( x + 2 ) · y ‘ = 1

Мы можем получить ряд дополнительных решений в тех случаях, когда существуют значения аргумента х , при которых функции f ( x ) и g ( x ) одновременно обращаются в 0 . В качестве дополнительного решения в уравнениях f ( x ) · y ‘ = g ( x ) при заданных значениях аргумента может выступать любая функция, определенная для заданного значения х .

Наличие дополнительных решений возможно для дифференциальных уравнений x · y ‘ = sin x , ( x 2 — x ) · y ‘ = ln ( 2 x 2 — 1 )

Ознакомиться с теоретической частью и примерами решения задач таких уравнений вы можете в разделе «Простейшие дифференциальные уравнения 1 -го порядка».

Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )

Поговорим теперь об уравнениях с разделенными переменными, которые имеют вид f ( y ) d y = g ( x ) d x . Как следует из названия, к данному виду дифференциальных уравнений относятся выражения, которые содержат переменные х и у , разделенные знаком равенства. Переменные находятся в разных частях уравнения, по обе стороны от знака равенства.

Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x

К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:

y 2 3 d y = sin x d x , e y d y = ( x + sin 2 x ) d x

Для того, чтобы прийти от ДУ с разделяющимися переменными к ДУ с разделенными переменными, необходимо разделить обе части уравнения на произведение f 2 ( y ) ⋅ g 1 ( x ) . Так мы придем к уравнению f 1 ( y ) f 2 ( y ) d y = g 2 ( x ) g 1 ( x ) d x . Преобразование можно будет считать эквивалентным в том случае, если одновременно f 2 ( y ) ≠ 0 и g 1 ( x ) ≠ 0 . Если хоть одно из условий не будет соблюдаться, мы можем потерять часть решений.

В качестве примеров дифференциальных уравнений с разделяющимися переменными можно привести следующие из них: d y d x = y · ( x 2 + e x ) , ( y 2 + a r c cos y ) · sin x · y ‘ = cos x y .

К уравнениям с разделяющимися переменными мы можем прийти от ряда дифференциальных уравнений других видов путем замены переменных. Например, мы можем подставить в исходное уравнение z = a x + b y . Это позволит нам перейти к дифференциальному уравнению с разделяющимися переменными от дифференциального уравнения вида y ‘ = f ( a x + b y ) , a , b ∈ R .

Подставив z = 2 x + 3 y в уравнение y ‘ = 1 e 2 x + 3 y получаем d z d x = 3 + 2 e z e z .

Заменив z = x y или z = y x в выражениях y ‘ = f x y или y ‘ = f y x , мы переходим к уравнениям с разделяющимися переменными.

Если произвести замену z = y x в исходном уравнении y ‘ = y x · ln y x + 1 , получаем x · d z d x = z · ln z .

В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.

Предположим, что в условии задачи нам дано уравнение y ‘ = y 2 — x 2 2 x y . Нам необходимо привести его к виду y ‘ = f x y или y ‘ = f y x . Для этого нам нужно разделить числитель и знаменатель правой части исходного выражения на x 2 или y 2 .

Нам дано уравнение y ‘ = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 , a 1 , b 1 , c 1 , a 2 , b 2 , c 2 ∈ R .

Для того, чтобы привести исходное уравнение к виду y ‘ = f x y или y ‘ = f y x , нам необходимо ввести новые переменные u = x — x 1 v = y — y 1 , где ( x 1 ; y 1 ) является решением системы уравнений a 1 x + b 1 y + c 1 = 0 a 2 x + b 2 y + c 2 = 0

Введение новых переменных u = x — 1 v = y — 2 в исходное уравнение y ‘ = 5 x — y — 3 3 x + 2 y — 7 позволяет нам получить уравнение вида d v d u = 5 u — v 3 u + 2 v .

Теперь выполним деление числителя и знаменателя правой части уравнения на u . Также примем, что z = u v . Получаем дифференциальное уравнение с разделяющимися переменными u · d z d u = 5 — 4 z — 2 z 2 3 + 2 z .

Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».

Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )

Приведем примеры таких уравнений.

К числу линейных неоднородных дифференциальных уравнений 1 -го порядка относятся:

y ‘ — 2 x y 1 + x 2 = 1 + x 2 ; y ‘ — x y = — ( 1 + x ) e — x

Для решения уравнений этого вида применяется метод вариации произвольной постоянной. Также мы можем представить искомую функцию у в виде произведения y ( x ) = u ( x ) v ( x ) . Алгоритмы применения обоих методов мы привели в разделе «Линейные неоднородные дифференциальные уравнения первого порядка».

Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a

Приведем примеры подобных уравнений.

К числу дифференциальных уравнений Бернулли можно отнести:

y ‘ + x y = ( 1 + x ) e — x y 2 3 ; y ‘ + y x 2 + 1 = a r c t g x x 2 + 1 · y 2

Для решения уравнений этого вида можно применить метод подстановки z = y 1 — a , которая выполняется для того, чтобы свести исходное уравнение к линейному дифференциальному уравнению 1 -го порядка. Также применим метод представления функции у в качестве y ( x ) = u ( x ) v ( x ) .

Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.

Уравнения в полных дифференциалах P ( x , y ) d x + Q ( x , y ) d y = 0

Если для любых значений x и y выполняется ∂ P ( x , y ) ∂ y = ∂ Q ( x , y ) ∂ x , то этого условия необходимо и достаточно, чтобы выражение P ( x , y ) d x + Q ( x , y ) d y представляло собой полный дифференциал некоторой функции U ( x , y ) = 0 , то есть, d U ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y . Таким образом, задача сводится к восстановлению функции U ( x , y ) = 0 по ее полному дифференциалу.

Выражение, расположенное в левой части записи уравнения ( x 2 — y 2 ) d x — 2 x y d y = 0 представляет собой полный дифференциал функции x 3 3 — x y 2 + C = 0

Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».

Дифференциальные уравнения второго порядка

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = 0 , p , q ∈ R

Линейное однородное дифференциальное уравнение с постоянными коэффициентами обычно решается достаточно просто. Нам необходимо найти корни характеристического уравнения k 2 + p k + q = 0 . Здесь возможны три варианта в зависимости от различных p и q :

• действительные и различающиеся корни характеристического уравнения k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
• действительные и совпадающие k 1 = k 2 = k , k ∈ R ;
• комплексно сопряженные k 1 = α + i · β , k 2 = α — i · β .

Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:

• y = C 1 e k 1 x + C 2 e k 2 x ;
• y = C 1 e k x + C 2 x e k x ;
• y = e a · x · ( C 1 cos β x + C 2 sin β x ) .

Пример 13

Предположим, что у нас есть линейное однородное дифференциальное уравнение 2 -го порядка с постоянными коэффициентами y ‘ ‘ + 3 y ‘ = 0 . Найдем корни характеристического уравнения k 2 + 3 k = 0 . Это действительные и различные k 1 = — 3 и k 2 = 0 . Это значит, что общее решение исходного уравнения будет иметь вид:

y = C 1 e k 1 x + C 2 e k 2 x ⇔ y = C 1 e — 3 x + C 2 e 0 x ⇔ y = C 1 e — 3 x + C 2

Восполнить пробелы в теоретической части и посмотреть подробный разбор примеров по теме можно в статье «Линейные однородные дифференциальные уравнения 2 -го порядка с постоянными коэффициентами».

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = f ( x ) , p , q ∈ R

Основным способом решение уравнений данного вида является нахождение суммы общего решения y 0 , которое соответствует линейному однородному дифференциальному уравнению y ‘ ‘ + p y ‘ + q y = 0 , и частного решения y

исходного уравнения. Получаем: y = y 0 + y

Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y

мы можем методом неопределенных коэффициентов при определенном виде функции f ( x ) , которая расположена в правой части записи исходного выражения. Также применим метод вариации произвольных постоянных.

К числу линейных неоднородных дифференциальных уравнений 2 -го порядка с постоянными коэффициентами относятся:

y ‘ ‘ — 2 y ‘ = ( x 2 + 1 ) e x ; y ‘ ‘ + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x

Теоретические выкладки и подробный разбор примеров по теме можно найти в разделе «ЛНДУ 2 -го порядка с постоянными коэффициентами».

Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )

Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.

На некотором отрезке [ a ; b ] общее решение линейного однородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 представлено линейной комбинацией двух линейно независимых частных решений y 1 и y 2 этого уравнения, то есть, y = C 1 y 1 + C 2 y 2 .

Частные решения мы можем выбрать из систем независимых функций:

1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 x , e k 2 x , . . . , e k n x 3 ) e k 1 x , x · e k 1 x , . . . , x n 1 · e k 1 x , e k 2 x , x · e k 2 x , . . . , x n 2 · e k 2 x , . . . e k p x , x · e k p x , . . . , x n p · e k p x 4 ) 1 , c h x , s h x

Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.

Возьмем для примера линейное однородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = 0 .

Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ, а y

частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y

нам поможет метод вариации произвольных постоянных.

Возьмем для примера линейное неоднородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = x 2 + 1 .

Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».

Дифференциальные уравнения высших порядков

Дифференциальные уравнения, допускающие понижение порядка

Мы можем провести замену y ( k ) = p ( x ) для того, чтобы понизить порядок исходного дифференциального уравнения F ( x , y ( k ) , y ( k + 1 ) , . . . , y ( n ) ) = 0 , которое не содержит искомой функции и ее производных до k — 1 порядка.

В этом случае y ( k + 1 ) = p ‘ ( x ) , y ( k + 2 ) = p ‘ ‘ ( x ) , . . . , y ( n ) = p ( n — k ) ( x ) , и исходное дифференциальное уравнение сведется к F 1 ( x , p , p ‘ , . . . , p ( n — k ) ) = 0 . После нахождения его решения p ( x ) останется вернуться к замене y ( k ) = p ( x ) и определить неизвестную функцию y .

Дифференциальное уравнение y ‘ ‘ ‘ x ln ( x ) = y ‘ ‘ после замены y ‘ ‘ = p ( x ) станет уравнением с разделяющимися переменными y ‘ ‘ = p ( x ) , и его порядок с третьего понизится до первого.

В уравнении, которое не содержит аргумента х и имеет вид F ( y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 , порядок может быть заменен на единицу следующим образом: необходимо провести замену d y d x = p ( y ) , где p ( y ( x ) ) будет сложной функцией. Применив правило дифференцирования, получаем:

d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.

Рассмотрим решение уравнения 4 y 3 y ‘ ‘ = y 4 — 1 . Путем замены d y d x = p ( y ) приведем исходное выражение к уравнению с разделяющимися переменными 4 y 3 p d p d y = y 4 — 1 .

Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».

Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x )

Решение уравнений данного вида предполагает выполнение следующих простых шагов:

• находим корни характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 ;
• записываем общее решение ЛОДУ y 0 в стандартной форме, а общее решение ЛНДУ представляем суммой y = y 0 + y

— частное решение неоднородного дифференциального уравнения.

Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y

целесообразно использовать метод вариации произвольных постоянных.

Линейному неоднородному ДУ с постоянными коэффициентами y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = x cos x + sin x соответствует линейное однородное ДУ y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = 0 .

Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».

Линейные однородные и неоднородные дифференциальные уравнения высших порядков y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 и y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )

Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ, а y

— частное решение неоднородного дифференциального уравнения.

y 0 представляет собой линейную комбинацию линейно независимых функций y 1 , y 2 , . . . , y n , каждая из которых является частным решением ЛОДУ, то есть, обращает равенство y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 в тождество. Частные решения y 1 , y 2 , . . . , y n обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.

После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y

Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».

Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2

Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.