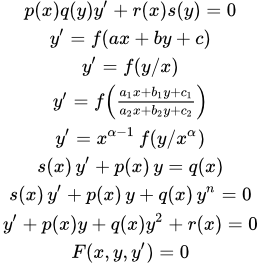Уравнение первого порядка разрешенное относительно первой производной

Дифференциальные уравнения первого порядка

Далее в тексте – функции своих аргументов. Штрих ′ означает производную по аргументу. – постоянные.

Дифференциальные уравнения первого порядка, разрешенные относительно производной

Как решать дифференциальные уравнения первого порядка

Пусть мы имеем дифференциальное уравнение первого порядка, разрешенное относительно производной:
.
Разделив это уравнение на , при , мы получим уравнение вида:
,
где .

Далее смотрим, не относятся ли эти уравнения к одному из перечисленных ниже типов. Если нет, то перепишем уравнение в форме дифференциалов. Для этого пишем и умножаем уравнение на . Получаем уравнение в форме дифференциалов:
.

Если это уравнение не является уравнением в полных дифференциалах, то считаем, что в этом уравнении – независимая переменная, а – это функция от . Разделим уравнение на :
.
Далее смотрим, не относится ли это уравнение к одному из, перечисленных ниже типов учитывая, что и поменялись местами.

Если и для этого уравнения не найден тип, то смотрим, нельзя ли упростить уравнение простой подстановкой. Например, если уравнение имеет вид:
,
то замечаем, что . Тогда делаем подстановку . После этого уравнение примет более простой вид:
.

Если и это не помогает, то пытаемся найти интегрирующий множитель ⇓.

Уравнения с разделяющимися переменными

Уравнения, приводящиеся к уравнениям с разделяющимися переменными

Делаем подстановку . Тогда
;
.
Далее разделяем переменные и интегрируем.
Подробнее >>>

Однородные уравнения

Решаем подстановкой:
,
где – функция от . Тогда
;
.
Разделяем переменные и интегрируем.
Подробнее >>>

Уравнения, приводящиеся к однородным

Вводим переменные и :
;
.
Постоянные и выбираем так, чтобы свободные члены обратились в нуль:
;
.
В результате получаем однородное уравнение в переменных и .
Подробнее >>>

Обобщенные однородные уравнения

Делаем подстановку . Получаем однородное уравнение в переменных и .
Подробнее >>>

Линейные дифференциальные уравнения

Есть три метода решения линейных уравнений.

1) Метод интегрирующего множителя.
Умножаем уравнение на интегрирующий множитель :
;
.
Далее интегрируем.
Подробнее >>>

2) Метод Бернулли.
Ищем решение в виде произведения двух функций и от переменной :
.
;
.
Одну из этих функций мы можем выбрать произвольным образом. Поэтому в качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Подробнее >>>

3) Метод вариации постоянной (Лагранжа).
Здесь мы сначала решаем однородное уравнение:

Общее решение однородного уравнения имеет вид:
,
где – постоянная. Далее мы заменяем постоянную на функцию , зависящую от переменной :
.
Подставляем в исходное уравнение. В результате получаем уравнение, из которого определяем .
Подробнее >>>

Уравнения Бернулли

Подстановкой уравнение Бернулли приводится к линейному уравнению.

Также это уравнение можно решать методом Бернулли. То есть ищем решение в виде произведения двух функций, зависящих от переменной :
.
Подставляем в исходное уравнение:
;
.
В качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .

Уравнения Риккати

Оно не решается в общем виде. Подстановкой

уравнение Риккати приводится к виду:
,
где – постоянная; ; .
Далее, подстановкой:

оно приводится к виду:
,
где .

Свойства уравнения Риккати и некоторые частные случаи его решения представлены на странице
Дифференциальное уравнение Риккати >>>

Уравнения Якоби

Уравнения в полных дифференциалах

При условии
.
При выполнении этого условия, выражение в левой части равенства является дифференциалом некоторой функции:
.
Тогда
.
Отсюда получаем интеграл дифференциального уравнения:
.

Для нахождения функции , наиболее удобным способом является метод последовательного выделения дифференциала. Для этого используют формулы:
;
;
;
.
Подробнее >>>

Интегрирующий множитель

Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то можно попытаться найти интегрирующий множитель . Интегрирующий множитель – это такая функция , при умножении на которую, дифференциальное уравнение становится уравнением в полных дифференциалах. Дифференциальное уравнение первого порядка имеет бесконечное число интегрирующих множителей. Однако, общих методов для нахождения интегрирующего множителя нет.
Подробнее >>>

Уравнения, не решенные относительно производной y’

Уравнения, допускающие решение относительно производной y’

Сначала нужно попытаться разрешить уравнение относительно производной . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.

Уравнения, допускающие разложение на множители

Если удастся уравнение разложить на множители:
,
то задача сводится к последовательному решению более простых уравнений:
;
;

;
Подробнее >>>

Уравнения, не содержащие x и y

Уравнения, не содержащие x или y

или
Ищем решение в параметрическом виде. Вводим параметр . Полагаем . Тогда
или .
Далее интегрируем уравнение:
;
.
В результате получаем выражение второй переменной через параметр .

Более общие уравнения:
или
также решаются в параметрическом виде. Для этого нужно подобрать такую функцию , чтобы из исходного уравнения можно было выразить или через параметр .
Чтобы выразить вторую переменную через параметр , интегрируем уравнение:
;
.
Подробнее >>>

Уравнения, разрешенные относительно y

Уравнения Клеро

Такое уравнение имеет общее решение

Подробнее >>>

Уравнения Лагранжа

Решение ищем в параметрическом виде. Полагаем , где – параметр.
Подробнее >>>

Уравнения, приводящиеся к уравнению Бернулли

Эти уравнения приводятся к уравнению Бернулли, если искать их решения в параметрическом виде, введя параметр и делая подстановку .
Подробнее >>>

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 20-05-2016

Дифференциальные уравнения 1-го порядка,
не разрешенные относительно производной

Уравнения 1-го порядка n-ой степени относительно производной

Пусть имеем дифференциальное уравнение

Решаем это уравнение относительно . Пусть

— вещественные решения уравнения (1).

Общий интеграл уравнения (1) выразится совокупностью интегралов:

где есть интеграл уравнения .

Таким образом, через каждую точку области, в которой принимает вещественные значения, проходит интегральных линий.

Пример 1. Решить уравнение .

Решение. Разрешим это уравнение относительно :

Пример 2. Решить уравнение .

Решение. Разрешим уравнение относительно переменной :

Положим , где — параметр; тогда получим Дифференцируя, найдем . Но так как , то будем иметь

Рассмотрим два случая:

1) , откуда , где — произвольная постоянная. Подставляя значение , получаем общее решение данного уравнения:

В равенстве нельзя заменить на и интегрировать полученное уравнение (так как при этом появится вторая произвольная постоянная, чего не может быть, поскольку рассматриваемое дифференциальное уравнение является уравнением первого порядка).

2) , откуда . Подставляя, получим еще одно решение .

Проверим, нарушится ли свойство единственности в каждой точке решения , т.е. является ли оно особым (см. часть 1.11). Для этого возьмем на интегральной кривой произвольную точку , где . Будем теперь искать решение, которое содержится в общем решении и график которого проходит через точку . Подставляя координаты этой точки в общее решение , будем иметь

откуда . Это значение постоянной подставим в . Тогда получим частное решение

которое не совпадает с решением . Для этих решений имеем соответственно . При обе производные совпадают. Следовательно, в точке нарушается свойство единственности, т. е. через эту точку проходят две интегральные кривые с одной и той же касательной. Так как произвольно, то единственность нарушается в каждой точке решения , а это означает, что оно является особым.

2°. Уравнения вида f(y,y’)=0 и f(x,y’)=0

Если уравнения и легко разрешимы относительно , то, разрешая их, получим уравнения с разделяющимися переменными. Рассмотрим случаи, когда эти уравнения не разрешимы относительно .

А. Уравнение вида разрешимо относительно :

Полагаем , тогда . Дифференцируя это уравнение и заменяя на , получим

Получаем общее решение уравнения в параметрической форме

Пример 3. Решить уравнение , где — постоянные.

Решение. Положим , тогда , или . Отсюда и .

Общим решением будет .

Б. Если уравнение вида неразрешимо (или трудно разрешимо) как относительно , так и относительно , но допускает выражение и через некоторый параметр :

то поступаем следующим образом. Имеем . С другой стороны, , так что и ; отсюда

Таким образом, получаем общее решение данного дифференциального уравнения в параметрической форме

Пример 4. Решить уравнение .

Решение. Полагаем , тогда имеем

Отсюда , общее решение .

В. Уравнение вида . Пусть это уравнение разрешимо относительно , то есть .

Полагая , получим . Но и, следовательно, , так что

Таким образом — общее решение уравнения в параметрической форме ( — параметр).

Замечание. В формулах нельзя рассматривать как производную. В них является просто параметром.

Пример 5. Решить уравнение .

Решение. Положим , тогда

Итак, — общее решение.

Аналогично случаю Б можно пытаться решать уравнение методом введения параметра .

3°. Уравнения Лагранжа

Уравнение Лагранжа имеет вид

Полагая , дифференцируя по и заменяя на , приводим это уравнение к линейному относительно как функции . Находя решение этого последнего уравнения , получаем общее решение исходного уравнения в параметрической форме:

Кроме того, уравнение Лагранжа может иметь еще особые решения вида , где — корень уравнения .

Пример 6. Проинтегрировать уравнение .

Решение. Полагаем , тогда . Дифференцируя, находим

Получили уравнение первого порядка, линейное относительно ; решая его, находим

Подставляя найденное значение в выражение для , получим окончательно

Уравнения Клеро

Уравнение Клеро имеет вид .

Метод решения тот же, что и для уравнения Лагранжа. Общее решение уравнения Клеро имеет вид

Уравнение Клеро может иметь еще особое решение, которое получается исключением из уравнений .

Пример 7. Проинтегрировать уравнение .

Решение. Полагая , получаем . Дифференцируя последнее уравнение и заменяя на , найдем

Приравнивая нулю первый множитель, получаем , откуда и общее решение исходного уравнения есть , однопараметрическое семейство прямых. Приравнивая нулю второй множитель, будем иметь . Исключая из этого уравнения и из уравнения , получим — это тоже решение нашего уравнения (особое решение).

С геометрической точки зрения кривая есть огибающая семейства прямых, даваемых общим решением (рис. 14).

Уравнение первого порядка разрешенное относительно первой производной

Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах…
Часть II. Глава IV. Обыкновенные дифференциальные уравнения

§ 1. Дифференциальные уравнения первого порядка

1. Основные понятия. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы) этой функции. Если независимая переменная одна, то уравнение называется обыкновенным; если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.

Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Например:

1) х²у’ + 5xy = у² – обыкновенное дифференциальное уравнение первого порядка;

2) – обыкновенное дифференциальное уравнение второго порядка;

3) y’³ + y»y»’ = х – обыкновенное дифференциальное уравнение третьего порядка;

4) F (х, у, у’, у») = 0 – общий вид обыкновенного дифференциального уравнения второго порядка;

5) – уравнение в частных производных первого порядка.

В этом параграфе рассматриваются обыкновенные дифференциальные уравнения первого порядка, т. е. уравнения вида F (х, у, у’) = 0 или (в разрешенном относительно у’ виде) y’ = f(х, у).

Решением дифференциального уравнения называется такая дифференцируемая функция у = φ (x), которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.

Общим решением дифференциального уравнения первого порядка у’ = f(x, у) в области D называется функция у = φ(x, C), обладающая следующими свойствами: 1) она является решением данного уравнения при любых значениях произвольной постоянной С, принадлежащих некоторому множеству; 2) для любого начального условия у(х0) = у0 такого, что (x0; y0) ∈ 0, существует единственное значение С = С0, при котором решение у = φ(x, C0) удовлетворяет заданному начальному условию.

Всякое решение у = φ(x, C0), получающееся из общего решения у = φ (x, C) при конкретном значении С = С0, называется частным решением.

Задача, в которой требуется найти частное решение уравнения y’ = f(х, у) удовлетворяющее начальному условию у(х0) = y0, называется задачей Коши.

Построенный на плоскости хОу график всякого решения у = φ(х) дифференциального уравнения называется интегральной кривой этого уравнения. Таким образом, общему решению у = φ(х, С) на плоскости хОу соответствует семейство интегральных кривых, зависящее от одного параметра – произвольной постоянной С, а частному решению, удовлетворяющему начальному условию y(x0) = y0, – кривая этого семейства, проходящая через заданную точку М0(x0; у0).

Если функция f(х, у) непрерывна и имеет непрерывную производную в области D, то решение дифференциального уравнения у’= f (х, у) при начальном условии у(х0) = у0 существует и единственно, т. е. через точку (x0; y0) проходит единственная интегральная кривая данного уравнения (теорема Коши).

Особым решением называется такое решение, во всех точках которого условие единственности не выполняется, т. е. в любой окрестности каждой точки (х; у) особого решения существуют по крайней мере две интегральные кривые, проходящие через эту точку.

Особые решения не получаются из общего решения дифференциального управления ни при каких значениях произвольной постоянной С (в том числе и при С = ± ∞).

Особым решением является огибающая семейства интегральных кривых (если она существует), т. е. линия, которая в каждой своей точке касается по меньшей мере одной интегральной кривой.

Например, общее решение уравнения записывается в виде у = sin (х + С). Это семейство интегральных кривых имеет две огибающие: у = 1 и у = -1, которые и будут особыми решениями.

2. Дифференциальные уравнения с разделяющимися переменными. Дифференциальное уравнение вида

относится к типу уравнений с разделяющимися переменными. Если ни одна из функций f1(x), f2(y), φ1(x), φ2(y) не равна тождественно нулю, то в результате деления исходного уравнения на f2 (x) φ1 (y) оно приводится к виду

Почленное интегрирование последнего уравнения приводит к соотношению

которое и определяет (в неявной форме) решение исходного уравнения. (Решение дифференциального уравнения, выраженное в неявной форме, называют интегралом этого уравнения.)

507. Решить уравнение х(у²-4)dx + y dy = 0.

△ Разделив обе части уравнения на у² – 4 ≠ 0, имеем

x² + ln|у² – 4| = ln|C|, или у² – 4 = Сe -λ²

Это общее решение данного дифференциального уравнения.

Пусть теперь у² – 4 = 0, т. е. у = ± 2. Непосредственной подстановкой убеждаемся, что у = ±2 – решение исходного уравнения. Но оно не будет особым решением, так как его можно получить из общего решения при С = 0. ▲

508. Найти частный интеграл уравнения у’ cos х = у / ln у, удовлетворяющий начальному условию y(0) = l.

△ Полагая , перепишем данное уравнение в виде

Проинтегрируем обе части уравнения:

, или

Используя начальное условие у = 1 при х = 0, находим С = 0. Окончательно получаем

▲

509. Найти общий интеграл уравнения у’ = tg x tg y.

△ Полагая и разделяя переменные, приходим к уравнению ctg у dy = tg х dx. Интегрируя, имеем

, или ln|sin у| = -ln|cos x| + ln С.

Отсюда находим sin y = C/cos x, или sin y / cos x = С (общий интеграл). ▲

510. Найти частное решение дифференциального уравнения (l + x²)dy + y dx = 0 при начальном условии у(1) = 1.

△ Преобразуем данное уравнение к виду . Интегрируя, получим

, или ln |y| = – arctg x + С

Это и есть общий интеграл данного уравнения.

Теперь, используя начальное условие, найдем произвольную постоянную С; имеем ln 1 = — arctg 1 + С, т. е. С = π/4. Следовательно,

ln у = – arctg х + π/4,

откуда получаем искомое частное решение y = e π/4 – arctg x . ▲

Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах… Ч. II. Стр. 117-119.