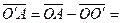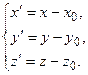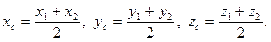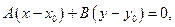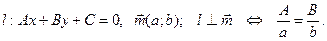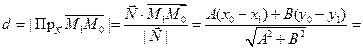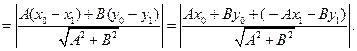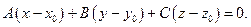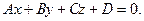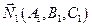Алгебраические уравнения поверхностей
Напомним, что многочленом степени одной переменной называется выражение вида
где — действительные числа (коэффициенты многочлена), — старший коэффициент, — свободный член. Степень многочлена обозначается .
Многочленом трех переменных называется выражение вида
называется степенью многочлена трёх переменных.
Алгебраической поверхностью называется множество точек, которое в какой-либо аффинной системе координат может быть задано уравнением вида
где — многочлен трех переменных .
Уравнение вида (4.11) называется алгебраическим уравнением с тремя неизвестными. Степенью уравнения (4.11) называется степень многочлена . Одна и та же поверхность может быть задана уравнением вида (4.11) с многочленами разных степеней. Порядком алгебраической поверхности называется наименьшая из степеней этих многочленов.
Всякую неалгебраическую поверхность называют трансцендентной.
В примере 4.1,а,б,в,г — поверхности алгебраические: а — первого порядка. б,в,г — второго порядка. Примером трансцендентной поверхности служит цилиндрическая поверхность (см. рисунок), образующие которой, параллельные оси , пересекают координатную плоскость в точках синусоиды . Эту линию нельзя задать уравнением вида (4.11).
Теорема (4.1) об инвариантности порядка алгебраической поверхности
Если в некоторой аффинной системе координат в пространстве поверхность задана уравнением (4.11), то и в любой другой аффинной системе координат эта поверхность задается уравнением того же вида (4.11) и той же степени. Другими словами, порядок алгебраической поверхности является инвариантом (остается неизменным в любой аффинной системе координат).
Теорема доказывается аналогично теореме 3.1.
В аналитической геометрии в пространстве изучаются:
– алгебраические поверхности первого порядка , описываемые алгебраическим уравнением первой степени с тремя неизвестными
– алгебраические поверхности второго порядка , описываемые алгебраическим уравнением второй степени с тремя неизвестными
1. Теорема 4.1 фактически выражает свойство многочленов: при линейной невырожденной замене переменных
где , степень многочлена не изменяется.
2. Алгебраическое уравнение (4.11) может не иметь действительных решений. Например, в пространстве нет точек, координаты которых удовлетворяют уравнению . Однако в области комплексных чисел, согласно основной теореме алгебры, любое алгебраическое уравнение имеет решения. Поэтому каждое алгебраическое уравнение (4.11) вида , где задает некоторую алгебраическую поверхность в трехмерном комплексном пространстве (см. пункт 2 замечаний 2.9). Если все точки этой поверхности вещественные (действительные), т.е. а то поверхность называют вещественной (действительной). В противном случае поверхность называют мнимой.
3. Алгебраическими неравенствами с тремя неизвестными называются неравенства вида
где — многочлен трех переменных . Степенью алгебраического неравенства называется степень многочлена .
4. Многочлены первой степени и алгебраические уравнения (неравенства) первой степени называются линейными.
5. Многочлен второй степени
называется также квадратичной функцией трех переменных; многочлен
называется квадратичной формой (квадратичной частью функции), многочлен — линейной формой (линейной частью функции), коэффициент — свободным членом. По сравнению со стандартной записью многочлена некоторые коэффициенты квадратичной функции удвоены для удобства выполнения алгебраических преобразований.
6. Квадратичную функцию (см. пункт 5) можно записать:
а) в матричном виде
где — матрица квадратичной функции; — расширенный (дополненный единицей) столбец переменных;
б) выделяя квадратичную и линейную части:
где — матрица квадратичной формы, — столбец коэффициентов линейной формы, — столбец переменных.
Матрицы и называются также матрицами малой и большой квадратичных форм квадратичной функции .
7. Многочлены второй степени и алгебраические уравнения (неравенства) второй степени называются квадратичными (квадратными).
8. Теорема 4.1, разумеется, справедлива для прямоугольных систем координат на плоскости. Напомним, что преобразования прямоугольных систем координат являются ортогональными (см. пункт 5 замечаний 2.3). Поэтому соответствующие этим преобразованиям линейные замены переменных (см. пункт 1) с ортогональной матрицей называются ортогональными (неоднородными при или однородными при ). Далее, как правило, будут рассматриваться уравнения, записанные в прямоугольной системе координат .
Уравнения прямой, виды уравнений прямой в пространстве
Материал этой статьи продолжает тему прямой в пространстве. От геометрического описания пойдем к алгебраическому: зададим прямую при помощи уравнений в фиксированной прямоугольной системе координат трехмерного пространства. Приведем общую информацию, расскажем о видах уравнений прямой в пространстве и их связи между собой.
Уравнение прямой в пространстве: общие сведения
Уравнение прямой на плоскости в прямоугольной системе координат O x y – это линейное уравнение с переменными x и y , которому отвечают координаты всех точек прямой и не удовлетворяют координаты никаких прочих точек.
Если речь идет о прямой в трехмерном пространстве, все несколько иначе: не существует такого линейного уравнения с тремя переменными x , y , z , которому бы отвечали только координаты точек заданной прямой. В самом деле, уравнение A x + B y + C z + D = 0 , где x , y , z – переменные, а А , В , С и D – некоторые действительные числа ( А , В , С одновременно не равны нулю) – это общее уравнение плоскости. Тогда как же задать прямую линию в прямоугольной системе координат O x y z ? Найдем ответ на этот вопрос в следующих пунктах темы.
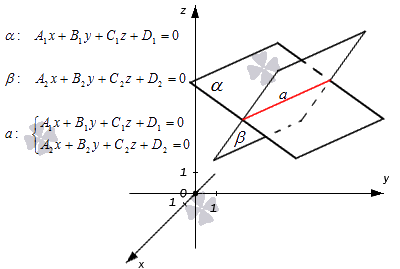
Уравнение прямой в пространстве как уравнение двух пересекающихся плоскостей
Когда две плоскости в пространстве имеют общую точку, существует их общая прямая, на которой находятся все общие точки этих плоскостей.
Рассмотрим это утверждение в алгебраическом толковании.
Допустим, в трехмерном пространстве зафиксирована прямоугольная система координат O x y z и задано, что прямая a – это линия пересечения двух плоскостей α и β , которые соответственно описываются уравнениями плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Поскольку прямая a – это множество общих точек плоскостей α и β , то координаты любой точки прямой a будут одновременно отвечать обоим уравнениям. Никакие прочие точки одновременно удовлетворять условия обоих уравнений не будут.
Таким образом, координаты любой точки прямой a в прямоугольной системе координат станут частным решением системы линейных уравнений вида
A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0
Общее же решение системы уравнений _ A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определит координаты каждой точки прямой a , т.е. по сути задает саму прямую a .
Резюмируем: прямая в пространстве в прямоугольной системе координат O x y z может быть задана системой уравнений двух плоскостей, которые пересекаются:
A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0
Приведем пример описания прямой линии в пространстве при помощи системы уравнений:
x + 3 y — 2 1 z + 11 3 y + 1 4 z — 2 = 0
Навык определения прямой линии уравнениями пересекающихся плоскостей необходим при решении задач на нахождение координат точки пересечения прямой и плоскости или нахождение координат точки пересечения двух прямых в пространстве.
Подробнее изучить эту тему можно, обратившись к статье об уравнениях прямой в пространстве, уравнениях двух пересекающихся прямых.
Заметим, что существует несколько способов описания прямой в пространстве. В практике прямую чаще задают не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, принадлежащей этой прямой. В подобных случаях легче задать канонические и параметрические уравнения прямой в пространстве. Поговорим о них ниже.
Параметрические уравнения прямой в пространстве
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , где x 1 , y 1 , z 1 – координаты некой точки прямой; а x , а y и a z (одновременно не равны нулю) – координаты направляющего вектора прямой. а · λ – некий параметр, принимающий любые действительные значения.
Любое значение параметра λ позволяет, используя параметрические уравнения прямой в пространстве, определить тройку чисел ( x , y , z ) , соответствующую некой точке прямой (отсюда и название такого вида уравнений). Например, пусть λ = 0 , тогда из параметрических уравнений прямой в пространстве получим координаты:
x = x 1 + a x · 0 y = y 1 + a y · 0 z = z 1 + a z · 0 ⇔ x = x 1 y = y 1 z = z 1
Рассмотрим конкретный пример:
Пусть прямая задана параметрическими уравнениями вида x = 3 + 2 · a x y = — 2 · a y z = 2 + 2 · a z .
Заданная прямая проходит через точку М 1 ( 3 , 0 , 2 ) ; направляющий вектор этой прямой имеет координаты 2 , — 2 , 2 .
Продолжение изучения этой темы можно найти в статье о параметрических уравнениях прямой в пространстве.
Канонические уравнения прямой в пространстве
Если разрешить каждое из параметрических уравнений прямой
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ относительно параметра λ , возможно просто перейти к каноническим уравнениям прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z .
Канонические уравнения прямой в пространстве задают прямую, которая проходит через точку М 1 ( x 1 , y 1 , z 1 ) , и у которой направляющий вектор равен a → = ( a x , a y , a z ) . Например, задана прямая, описываемая каноническим уравнением x — 1 1 = y 2 = z + 5 7 . Эта прямая проходит через точку с координатами ( 1 , 0 , — 5 ) , ее направляющий вектор имеет координаты ( 1 , 2 , — 7 ) .
Отметим, что одно или два числа из чисел а x , а y и а z в канонических уравнениях прямой могут быть равны нулю (все три числа не могут быть равны нулю, поскольку направляющий вектор не может быть нулевым). В таком случае запись вида x — x 1 a x = y — y 1 a y = z — z 1 a z является формальной (поскольку в знаменателях одной или двух дробей будут нули) и понимать ее нужно как:
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , где λ ∈ R .
Если одно из чисел а x , а y и a z канонического уравнения прямой равно нулю, то прямая лежит в какой-то из координатных плоскостей, или в плоскости, ей параллельной. Если два из чисел а x , а y и a z равны нулю, то прямая или совпадает с какой-либо из координатных осей, или параллельна ей. К примеру, прямая, описываемая каноническим уравнением x + 4 3 = y — 5 2 = z + 2 0 , лежит в плоскости z = — 2 , параллельной координатной плоскости O x y , а координатная ось O y описывается каноническими уравнениями x 0 = y 1 = z 0 .
Графические иллюстрации подобных случаев, составление канонических уравнений прямой в пространстве, примеры решения типовых задач, а также алгоритм перехода от канонических уравнений к другим видам уравнений прямой в пространстве рассмотрены в статье о канонических уравнениях прямой в пространстве.
Аналитическая геометрия на плоскости и в пространстве. 1 страница
В этой главе мы изучим фигурах первого и второго порядка на плоскости и в пространстве.
§2.1.Декартова прямоугольная система координат.
2.1.1. Определение. Аффинной (декартовой) системой координатв трехмерном пространстве называется совокупность некоторой точки и произвольного базиса. При этом точка называется началом координат, а прямые, проходящие через начало координат в направлении базисных векторов – осями координат: первая – осью абсцисс (ОХ), вторая – осью ординат (ОY), третья – осью аппликат (OZ).
Аналогично определяются аффинные системы координат на плоскости и прямой.
2.1.2. Определение. Вектор, соединяющий начало координат с некоторой точкой, называется радиусом-вектором этой точки.
2.1.3. Определение. Координатами точки в аффинной системе координат называются координаты ее радиуса-вектора.
2.1.4. Определение. Аффинная система координат, базис которой является ортонормированным, называется прямоугольной декартовой системой координат.

Пусть новая система координат 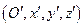
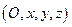
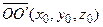


2.1.6. Кривые и поверхности.
Одним из основных вопросов аналитической геометрии является исследование линий на плоскости и поверхностей в пространстве.
2.1.6.1. Определение. Уравнение f(x, y) = 0 называется уравнением линии l на плоскости, если этому уравнению удовлетворяют координаты х, у всех точек М(х, у), лежащих на линии, и не удовлетворяют координаты ни одной точки P(х, у), не лежащей на кривой:
f(x, y) = 0 
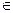
f(x, y) 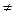
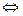

2.1.6.2. Определение. Уравнение F(x, y, z) = 0 называется уравнением поверхности 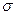
F(x, y, z) = 0 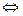
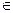
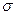
F(x, y, z) 

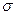
2.1.7. Две основные задачи аналитической геометрии.
I.Дано некоторое множество точек плоскости (пространства), обладающее некоторым набором свойств. Требуется составить уравнение (или систему уравнений), которое в некоторой системе координат задает это множество точек.
II (обратная). В заданной системе координат некоторое множество точек плоскости (пространства) описывается заданным уравнением (или системой уравнений). Требуется определить вид и основные свойства этого множества и построить его эскиз.
§2.2.Простейшие задачи аналитической геометрии.
2.2.1. Нахождение длины отрезка.
Пусть в заданной декартовой прямоугольной системе координат имеется две точки 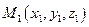

Вектор 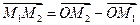
Следовательно, длина отрезка 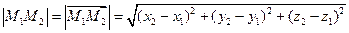
2.2.2. Деление отрезка в заданном отношении.
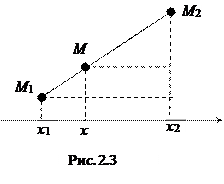
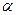
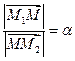
Запишем векторное равенство 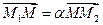
В частном случае 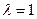
§2.3. Прямая на плоскости.
2.3.1. Общее уравнение прямой.
2.3.1.1. Определение. Ненулевой вектор 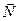
2.3.1.2. Теорема. (Общее уравнение прямой)

Пусть на плоскости задана точка 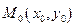
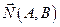
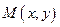
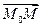
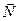

(скалярное произведение ортогональных векторов равно нулю).
Запишем последнее равенство в координатной форме: 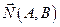
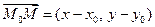
Ах + Ву + (–Ах0 – Ву0) = 0. Обозначим С = –Ах0 – Ву0, тогда 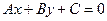
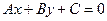
2.1.3.3. Определение. Уравнение вида
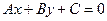
называется общим уравнением прямой.
2.1.3.4. Определение. Уравнение вида
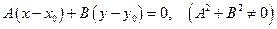
называется уравнением прямой, проходящей через точку 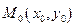
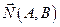
2.1.3.5. Определение. Линии, которые в декартовой прямоугольной системе координат задаются уравнениями первой степени, называются линиями первого порядка.
2.3.1.6. Теорема. (О линиях первого порядка на плоскости)
Линиями первого порядка на плоскости являются прямые, и только они.
То, что прямая на плоскости задается уравнением вида 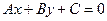
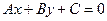

Пусть 

Вычтем полученное равенство из уравнения (2.1), получим
то есть уравнение прямой, проходящей через точку 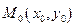
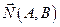

Таким образом, доказано, что всякое уравнение вида (2.1) при условии 
2.3.1.7. Теорема. (О перпендикулярности прямой и вектора на плоскости)
Для того, чтобы прямая, заданная общим уравнением, была перпендикулярна вектору на плоскости, необходимо и достаточно, чтобы координаты вектора были пропорциональны коэффициентам при переменных общего уравнения прямой, т.е.
Очевидно, перпендикулярность прямой и вектора эквивалентно коллинеарности вектора и нормального вектора прямой, следовательно, по критерию коллинеарности (Следствие из теоремы 1.5.6) получаем требуемое.
2.3.1.8. Частные случаи общего уравнения прямой на плоскости.
1. 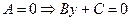
2. 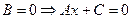
3. 
4. 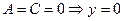
5. 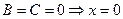
2.3.2. Уравнение прямой с угловым коэффициентом.
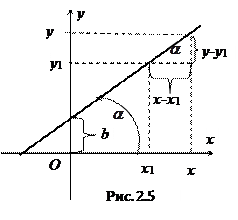
2.3.2.1. Определение. Углом наклона прямой называется любой направленный угол, на который надо повернуть ось Ох, чтобы получить одно из направлений прямой.
Очевидно, все углы наклона прямой отличаются друг от друга на величину 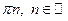
2.3.2.2. Вывод уравнения прямой с угловым коэффициентом.
Рассмотрим точку 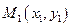
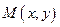
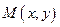
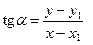
Обозначим 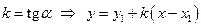
Полагая 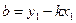
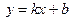
Геометрический смысл коэффициента 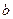
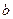
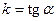
Уравнение вида (2.3) называется уравнением прямой с угловым коэффициентом.
Так как 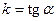
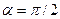
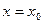
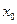
2.3.3. Связь между общим уравнением прямой и уравнением прямой с угловым коэффициентом.
Запишем уравнение прямой с угловым коэффициентом 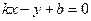
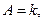
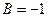
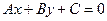
Обратный переход: если в уравнении 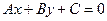
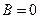
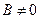
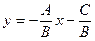
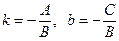
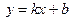
2.3.4. Уравнение прямой в отрезках.
Рассмотрим прямую, не проходящую через начало координат и заданную своим общим уравнением 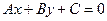
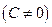


Обозначая 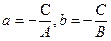
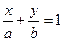
которое называется уравнением прямой в отрезках.
Положив в этом уравнении х = 0, получим y = b; положив у = 0, получаем х = а. Таким образом, параметры а и b равны, соответственно, абсциссе и ординате концов отрезков, отсекаемых прямой на осях Ох и Оу. Отметим, что в отрезках может быть записана любая прямая, не проходящая через начало координат.
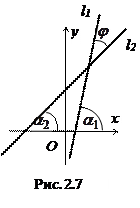
прямая l2 задана уравнением у = k2х + b2; тогда 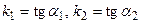
Так как 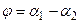
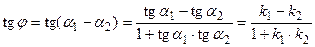
Таким образом, 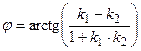
Если прямые заданы своими общими уравнениями
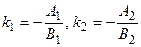
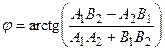
2.3.5.1. Условия параллельности и перпендикулярности прямых на плоскости.
Из выражений для тангенса угла между прямыми следуют условия параллельности и перпендикулярности прямых:
В случае параллельности прямых l1|| l2 тангенс угла между ними
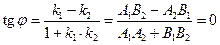
следовательно, k1 = k2, или А1В2 = А2В1, или 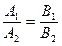
В случае параллельности прямых 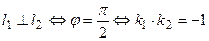
2.3.6. Расстояние от точки до прямой на плоскости.

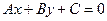
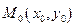
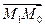
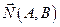


Из принадлежности точки М1 прямой l следует, что 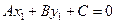

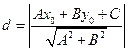
Таким образом, чтобы найти расстояние от точки до прямой, достаточно подставить координаты точки в общее уравнение прямой и полученное число разделить на длину нормального вектора.
§2.4. Плоскость в пространстве.
2.4.1. Общее уравнение плоскости.
2.4.1.1. Определение. Вектор, перпендикулярный к плоскости, называется ее нормальным вектором.
2.4.1.2. Теорема. (Общее уравнение плоскости).

Пусть в пространстве задан ненулевой вектор 
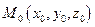
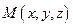
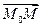
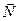
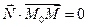
(скалярное произведение ортогональных векторов равно нулю).
В координатном виде это уравнение имеет вид
Преобразуем это уравнение: 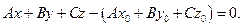
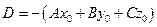
2.4.1.3. Определение. Уравнение вида
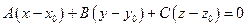
называется уравнением плоскости, проходящей через точку 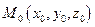

2.4.1.4. Определение. Уравнение вида
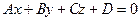
называется общим уравнением плоскости.
2.4.1.5. Связка плоскостей.
Связкой плоскостей называют совокупность плоскостей, проходящих через одну точку. Очевидно, уравнение 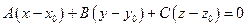
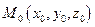
2.4.1.6. Определение. Поверхность в пространстве, которая в декартовой прямоугольной системе координат задается уравнением первой степени, называется поверхностью первого порядка.
2.4.1.7. Теорема. (О поверхностях первого порядка в пространстве).
Поверхностями первого порядка в пространстве являются плоскости, и только они.
Поскольку мы уже доказали в теореме 2.4.1.2, что плоскость можно задать уравнением первого порядка, осталось доказать, что уравнение 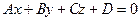
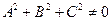
Пусть 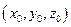
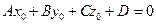
Вычтем полученное равенство из уравнения (2.7), получим
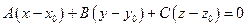
то есть уравнение плоскости, проходящей через точку 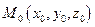

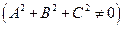
Таким образом, доказано, что всякое уравнение вида (2.7) при условии 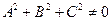
2.4.1.8. Частные случаи общего уравнения плоскости.
1. 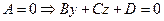
2. 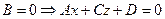
3. 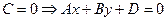
4. 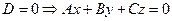
5. 
6. 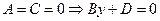
7. 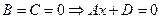
8. 
9. 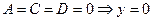
10. 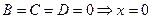
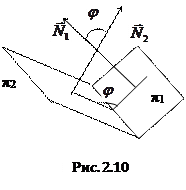
Пусть даны две плоскости
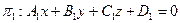
и 
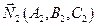
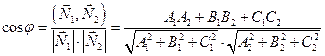
Если требуется определить острый угол между плоскостями, то
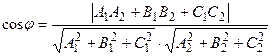
Из формулы угла между плоскостями следуют условия параллельности и перпендикулярности плоскостей.
Дата добавления: 2016-04-14 ; просмотров: 2684 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenija-prjamoj-vidy-uravnenij-prjamoj-v-prostr/
http://helpiks.org/7-85715.html