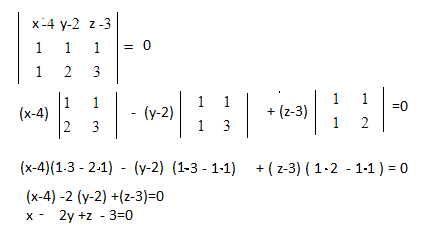Уравнение плоскости через две точки перпендикулярно плоскости

Уравнение плоскости, проходящей через заданную точку перпендикулярно к двум заданным пересекающимся плоскостям.

В этой статье содержится ответ на вопрос: «Как написать уравнение плоскости, проходящей через заданную точку перпендикулярно к двум заданным плоскостям»? Сначала приведены необходимые теоретические сведения, а также рассуждения, помогающие составить уравнение плоскости, проходящей через заданную точку перпендикулярно к двум пересекающимся плоскостям. После этого разобраны решения характерных примеров и задач.

Навигация по странице.

Нахождение уравнения плоскости, проходящей через заданную точку пространства перпендикулярно к двум заданным плоскостям.

Начнем с постановки задачи.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана точка и две пересекающиеся плоскости и . Требуется написать уравнение плоскости , проходящей через точку М₁ перпендикулярно к плоскостям и .

Заметим, что плоскость , уравнение которой нам требуется составить, перпендикулярна к прямой, по которой пересекаются плоскости и . Действительно, из признака перпендикулярности двух плоскостей следует, что плоскость, перпендикулярная линии пересечения двух плоскостей, перпендикулярна к каждой из этих плоскостей. Более того, существует только одна плоскость, проходящая через заданную точку пространства перпендикулярно двум пересекающимся плоскостям, так как существует только одна плоскость, проходящая через заданную точку перпендикулярно к заданной прямой.

Теперь приступим именно к решению поставленной задачи.

Из условия нам известны координаты точки , через которую проходит плоскость . Если мы найдем координаты нормального вектора плоскости , то сможем записать общее уравнение плоскости, проходящей через заданную точку с заданным нормальным вектором, в виде , где — нормальный вектор плоскости .

Итак, наша задача сводится к нахождению координат нормального вектора плоскости . В свою очередь нормальный вектор плоскости есть направляющий вектор прямой, по которой пересекаются две заданные плоскости и , так как плоскость перпендикулярна к пересекающимся плоскостям и . В частности, если плоскости и заданы общими уравнениями плоскостей вида и соответственно, то направляющим вектором прямой, по которой пересекаются плоскости и , является векторное произведение векторов и (об этом написано в разделе координаты направляющего вектора прямой, по которой пересекаются две заданные плоскости).

Чтобы написать уравнение плоскости, проходящей через заданную точку перпендикулярно к двум пересекающимся плоскостям и , нужно

• найти координаты направляющего вектора прямой, по которой пересекаются заданные плоскости и ;
• принять эти координаты за соответствующие координаты А , В и С нормального вектора плоскости, уравнение которой мы ищем;
• написать уравнение плоскости вида — это и есть искомое уравнение плоскости, проходящей через заданную точку перпендикулярно к двум пересекающимся плоскостям и .

Чтобы все стало понятно, предлагаем перейти к следующему пункту и ознакомиться с подробным решением примеров, в которых находится уравнение плоскости, проходящей через заданную точку пространства перпендикулярно к двум заданным пересекающимся плоскостям.

Примеры составления уравнения плоскости, проходящей через заданную точку перпендикулярно к двум заданным плоскостям.

Начнем с задачи на нахождение уравнения плоскости, перпендикулярной к двум координатным плоскостям.

Задача 29252 5.2.20) Составить уравнение плоскости.

Условие

5.2.20) Составить уравнение плоскости, проходящей через точки M1(4; 2; 3) и М2 (2; 0; 1) и перпендикулярной к плоскости х + 2у + 3z + 4 = 0.

Решение

Пусть M(x;y;z) произвольная точка плоскости
Значит векторы
vector=(x-4;y-2;z-3);
vector=(2-4;0-2;1-3)=(-2;-2;-2)
и нормальный вектор vector=(1;2;3>
[b]компланарны [/b].

Условие [b]компланарности[/b] векторов, заданных
координатами — равенство нулю определителя третьего порядка,
составленного из координат векторов.

Вместо вектора vector=(-2;-2;-2) можно
можно взять коллинеарный ему вектор с координатами (1;1;1)

О т в е т. х-2у+z-3=0

Уравнение плоскости.

Общее уравнение плоскости

Любую плоскость можно задать уравнением плоскости первой степени вида

A x + B y + C z + D = 0

где A, B и C не могут быть одновременно равны нулю.

Уравнение плоскости в отрезках

Если плоскость пересекает оси OX, OY и OZ в точках с координатами ( a , 0, 0), (0, b , 0) и (0, 0, с ), то она может быть найдена, используя формулу уравнения плоскости в отрезках

Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали

Чтобы составить уравнение плоскости, зная координаты точки плоскости M( x ₀, y ₀, z ₀) и вектора нормали плоскости n = < A; B; C >можно использовать следующую формулу.

Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой

Если заданы координаты трех точек A( x ₁, y ₁, z ₁), B( x ₂, y ₂, z ₂) и C( x ₃, y ₃, z ₃), лежащих на плоскости, то уравнение плоскости можно найти по следующей формуле

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.