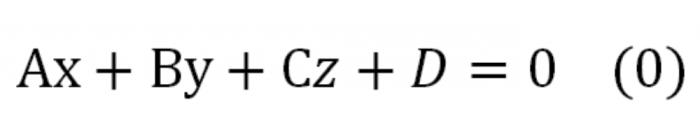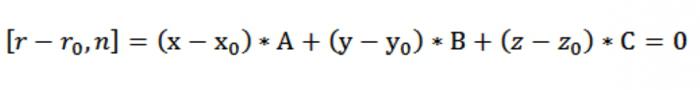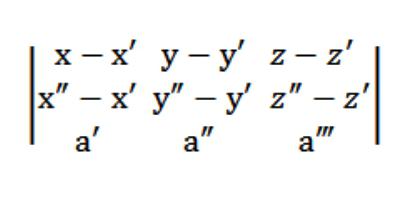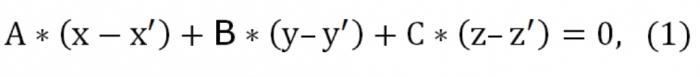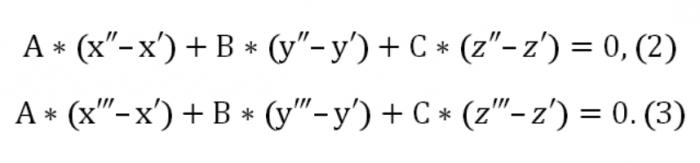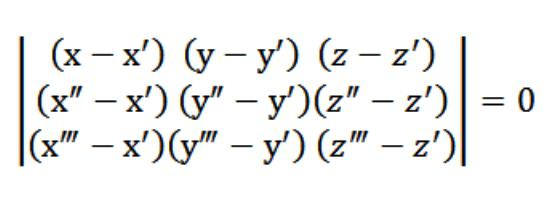Уравнение плоскости через радиус вектор

Векторное уравнение плоскости

Кроме того, плоскость может быть описана с помощью точки и вектора, перпендикулярного плоскости, называемой нормальным вектором.

Векторное уравнение плоскости имеет следующий вид:

Параметрическое уравнение → Векторное уравнение

Метод

1. Примите вектор положения из параметрического уравнения
2. Вычислите нормальный вектор
   • Вариант 1: используйте скалярное произведение
   • Вариант 2: используйте перекрестное произведение векторов
3. Вставьте вектор положения и нормальный вектор

Подсказка

Например

Вектор положения

Нормальный вектор

Вариант 1

Поскольку оба вектора направления перпендикулярны нормальному вектору $\vec=\begin x \\ y \\ z \end$, скалярное произведение должно привести к нулю.

Теперь можно вычислить скалярное произведение.

Выберите любое значение $z$ , например $z=4$

Вычислите $x$, используя I. (вставьте $y$)

Вариант 2

Теперь мы вычисляем только перекрестное произведение векторов.

Вставьте

$\text \left(\vec — \begin 2 \\ 1 \\ 1 \end\right) \cdot \begin 2 \\ -2 \\ 4 \end=0$

Векторное уравнение → параметрическое уравнение

Метод

1. Примите вектор положения, векторного уравнения
2. Используйте скалярное произведение для определения вектора направления
3. Вставьте вектор положения и вектор направления

Подсказка

Например

$\text \left(\vec — \begin 2 \\ 1 \\ 1 \end\right) \cdot \begin 2 \\ -2 \\ 4 \end=0$

Вектор положения

Вектор направления

Используя нормальный вектор, мы можем определить оба вектора направления, необходимые для Параметрического уравнения.

1. Вектор направления

Должен быть найден вектор, с которым скалярное произведение равно нулю.

Особенно легко заменить первую координату на 0,а затем поменять местами две другие координаты и изменить знак.

2 Вектор направления

Здесь последняя координата должна быть заменена на 0, а две другие координаты должны изменить знак.

Вставьте

$\text \vec = \begin 2 \\ 1 \\ 1 \end + r \cdot \begin 0 \\ -4 \\ -2 \end$ $+ s \cdot \begin -2 \\ -2 \\ 0 \end$

Уравнения прямых и плоскостей

Поверхности и линии первого порядка.

Уравнение первой степени, или линейное уравнение, связывающее координаты точки в пространстве, имеет вид
$$
Ax+By+Cz+D = 0,\label
$$
причем предполагается, что коэффициенты при переменных не равны нулю одновременно, то есть \(A^<2>+B^<2>+C^ <2>\neq 0\). Аналогично, линейное уравнение, связывающее координаты точки на плоскости, — это уравнение
$$
Ax+By+C = 0,\label
$$
при условии \(A^<2>+B^ <2>\neq 0\).

В школьном курсе доказывается, что в декартовой прямоугольной системе координат уравнения \eqref и \eqref определяют соответственно плоскость и прямую линию на плоскости. Из теорем о порядке алгебраических линий и поверхностей следует, что то же самое верно и в общей декартовой системе координат. Точнее, имеют место следующие теоремы.

В общей декартовой системе координат в пространстве каждая плоскость может быть задана линейным уравнением
$$
Ax+By+Cz+D = 0.\nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат определяет плоскость.

В общей декартовой системе координат на плоскости каждая прямая может быть задана линейным уравнением
$$
Ax+By+C = 0,\nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат на плоскости определяет прямую.

Эти теоремы полностью решают вопрос об уравнениях плоскости и прямой линии на плоскости. Однако ввиду важности этих уравнений мы рассмотрим их в других формах. При этом будут получены независимые доказательства теорем этого пункта.

Параметрические уравнения прямой и плоскости.

Мы будем предполагать, что задана декартова система координат в пространстве (или на плоскости, если мы изучаем прямую в планиметрии). Это, в частности, означает, что каждой точке сопоставлен ее радиус-вектор относительно начала координат.

Рис. 6.1

Вектор \(\overrightarrowM> = \boldsymbol-\boldsymbol_<0>\), начало которого лежит на прямой, параллелен прямой тогда и только тогда, когда \(M\) также лежит на прямой. В этом и только этом случае для точки \(M\) найдется такое число \(t\), что
$$
\boldsymbol-\boldsymbol_ <0>= t\boldsymbol.\label
$$

Наоборот, какое бы число мы ни подставили в формулу \eqref в качестве \(t\), вектор \(\boldsymbol\) в этой формуле определит некоторую точку на прямой.

Уравнение \eqref называется векторным параметрическим уравнением прямой, а переменная величина \(t\), принимающая любые вещественные значения, называется параметром.

Векторное параметрическое уравнение выглядит одинаково и в планиметрии, и в стереометрии, но при разложении по базису оно сводится к двум или трем скалярным уравнениям, смотря по тому, сколько векторов составляют базис.

Получим теперь параметрические уравнения плоскости. Обозначим через \(\boldsymbol

\) и \(\boldsymbol\) ее направляющие векторы, а через \(\boldsymbol_<0>\) — радиус-вектор ее начальной точки \(M_<0>\). Пусть точка \(M\) с радиус-вектором \(\boldsymbol\) — произвольная точка пространства (рис. 6.2).

Рис. 6.2

Вектор \(\overrightarrowM> = \boldsymbol-\boldsymbol_<0>\), начало которого лежит на плоскости, параллелен ей тогда и только тогда, когда его конец \(M\) также лежит на плоскости. Так как \(\boldsymbol

\) и \(\boldsymbol\) не коллинеарны, в этом и только этом случае \(\boldsymbol-\boldsymbol_<0>\) может быть по ним разложен. Поэтому, если точка \(M\) лежит в плоскости (и только в этом случае), найдутся такие числа \(t_<1>\) и \(t_<2>\), что
$$
\boldsymbol-\boldsymbol_ <0>= t_<1>\boldsymbol

+t_<2>\boldsymbol.\label
$$

Это уравнение называется параметрическим уравнением плоскости. Каждой точке плоскости оно сопоставляет значения двух параметров \(t_<1>\) и \(t_<2>\). Наоборот, какие бы числа мы ни подставили как значения \(t_<1>\) и \(t_<2>\), уравнение \eqref определит некоторую точку плоскости.

Пусть \((x, y, z)\) и \((x_<0>, y_<0>, z_<0>)\) — координаты точек \(M\) и \(M_<0>\) соответственно, а векторы \(\boldsymbol

\) и \(\boldsymbol\) имеют компоненты \((p_<1>, p_<2>, p_<3>)\) и \((q_<1>, q_<2>, q_<3>)\). Тогда, раскладывая по базису обе части уравнения \eqref, мы получим параметрические уравнения плоскости
$$
x-x_ <0>= t_<1>p_<1>+t_<2>q_<1>,\ y-y_ <0>= t_<1>p_<2>+t_<2>q_<2>,\ z-z_ <0>= t_<1>p_<3>+t_<2>q_<3>.\label
$$

Отметим, что начальная точка и направляющий вектор прямой образуют на ней ее внутреннюю декартову систему координат. Значение параметра \(t\), соответствующее какой-то точке, является координатой этой точки во внутренней системе координат. Точно так же на плоскости начальная точка и направляющие векторы составляют внутреннюю систему координат, а значения параметров, соответствующие точке, — это ее координаты в этой системе.

Прямая линия на плоскости.

Поэтому мы можем сформулировать следующее утверждение.

В любой декартовой системе координат на плоскости уравнение прямой с начальной точкой \(M_<0>(x_<0>, y_<0>)\) и направляющим вектором \(\boldsymbol(a_<1>, a_<2>)\) может быть записано в виде \eqref.

Уравнение \eqref линейное. Действительно, после преобразования оно принимает вид \(a_<2>x-a_<1>y+(a_<1>y_<0>-a_<2>x_<0>) = 0\), то есть \(Ax+By+C = 0\), где \(A = a_<2>\), \(B = -a_<1>\) и \(C = a_<1>y_<0>-a_<2>x_<0>\).

Вектор с координатами \((-B, A)\) можно принять за направляющий вектор прямой с уравнением \eqref в общей декартовой системе координат, а точку \eqref за начальную точку.

Если система координат декартова прямоугольная, то вектор \(\boldsymbol(A, B)\) перпендикулярен прямой с уравнением \eqref.

Действительно, в этом случае \((\boldsymbol, \boldsymbol) = -BA+AB = 0\).

Пусть в уравнении прямой \(Ax+By+C = 0\) коэффициент \(B\) отличен от нуля. Это означает, что отлична от нуля первая компонента направляющего вектора, и прямая не параллельна оси ординат. В этом случае уравнение прямой можно представить в виде
$$
y = kx+b,\label
$$
где \(k = -A/B\), а \(b = -C/B\). Мы видим, что к равно отношению компонент направляющего вектора: \(k = a_<2>/a_<1>\) (рис. 6.3).

Рис. 6.3. k=-1. Прямая y=-x+1/2

Отношение компонент направляющего вектора \(a_<2>/a_<1>\) называется угловым коэффициентом прямой.

Угловой коэффициент прямой в декартовой прямоугольной системе координат равен тангенсу угла, который прямая образует с осью абсцисс. Угол этот отсчитывается от оси абсцисс в направлении кратчайшего поворота от \(\boldsymbol_<1>\) к \(\boldsymbol_<2>\) (рис. 6.4).

Рис. 6.4. \(k=\operatorname\varphi = -1\). Прямая \(y=-x+1/2\)

Положив \(x = 0\) в уравнении \eqref, получаем \(y = b\). Это означает, что свободный член уравнения \(b\) является ординатой точки пересечения прямой с осью ординат.

Если же в уравнении прямой \(B = 0\) и ее уравнение нельзя представить в виде \eqref, то обязательно \(A \neq 0\). В этом случае прямая параллельна оси ординат и ее уравнению можно придать вид \(x = x_<0>\), где \(x_ <0>= -C/A\) — абсцисса точки пересечения прямой с осью абсцисс.

Векторные уравнения плоскости и прямой.

Параметрическое уравнение плоскости утверждает, что точка \(M\) лежит на плоскости тогда и только тогда, когда разность ее радиус-вектора и радиус-вектора начальной точки \(M_<0>\) компланарна направляющим векторам \(\boldsymbol

\) и \(\boldsymbol\). Эту компланарность можно выразить и равенством
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol

, \boldsymbol) = 0.\label
$$
Вектор \(\boldsymbol = [\boldsymbol

, \boldsymbol]\) — ненулевой вектор, перпендикулярный плоскости. Используя его, мы можем записать уравнение \eqref в виде
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol) = 0.\label
$$

Уравнения \eqref и \eqref называют векторными уравнениями плоскости. Им можно придать форму, в которую не входит радиус-вектор начальной точки. Например, положив в \eqref \(D = -(\boldsymbol_<0>, \boldsymbol)\), получим
$$
(\boldsymbol, \boldsymbol)+D = 0.\label
$$

Для прямой на плоскости можно также написать векторные уравнения, аналогичные \eqref и \eqref,
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol) = 0\ \mbox<или>\ (\boldsymbol, \boldsymbol)+C = 0.\nonumber
$$
Первое из них выражает тот факт, что вектор \(\boldsymbol-\boldsymbol_<0>\) перпендикулярен ненулевому вектору \(\boldsymbol\), перпендикулярному направляющему вектору \(\boldsymbol\), и потому коллинеарен \(\boldsymbol\).

Пусть \(x, y, z\) — компоненты вектора \(\boldsymbol\) в общей декартовой системе координат. Тогда скалярное произведение \((\boldsymbol-\boldsymbol_<0>, \boldsymbol)\) при \(\boldsymbol \neq 0\) записывается линейным многочленом \(Ax+By+Cz+D\), где \((A^<2>+B^<2>+C^ <2>\neq 0)\).

Обратно, для любого линейного многочлена найдутся такие векторы \(\boldsymbol_<0>\) и \(\boldsymbol \neq 0\), что в заданной общей декартовой системе координат \(Ax+By+Cz+D = (\boldsymbol-\boldsymbol_<0>, \boldsymbol)\).

Первая часть предложения очевидна: подставим разложение вектора \(\boldsymbol\) по базису в данное скалярное произведение:
$$
(x\boldsymbol_<1>+y\boldsymbol_<2>+z\boldsymbol_<3>-\boldsymbol_<0>, \boldsymbol),\nonumber
$$
раскроем скобки и получим многочлен \(Ax+By+Cz+D\), в котором \(D = -(\boldsymbol_<0>, \boldsymbol)\) и
$$
A = (\boldsymbol_<1>, \boldsymbol),\ B = (\boldsymbol_<2>, \boldsymbol),\ C = (\boldsymbol_<3>, \boldsymbol)\label
$$
\(A\), \(B\) и \(C\) одновременно не равны нулю, так как ненулевой вектор \(\boldsymbol\) не может быть ортогонален всем векторам базиса.

Для доказательства обратного утверждения найдем сначала вектор \(\boldsymbol\) из равенств \eqref, считая \(A\), \(B\) и \(C\) заданными. Из ранее доказанного утверждения 10 следует, что
$$
\boldsymbol = \frac_<2>, \boldsymbol_<3>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>+\frac_<3>, \boldsymbol_<1>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>+\frac_<1>, \boldsymbol_<2>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>.\label
$$

Вектор \(\boldsymbol_<0>\) должен удовлетворять условию \(D = -(\boldsymbol_<0>, \boldsymbol)\). Один из таких векторов можно найти в виде \(\boldsymbol_ <0>= \lambda \boldsymbol\). Подставляя, видим, что \(-\lambda(\boldsymbol, \boldsymbol) = D\), откуда \(\boldsymbol_ <0>= -D\boldsymbol/|\boldsymbol|^<2>\).

Итак, мы нашли векторы \(\boldsymbol\) и \(\boldsymbol_<0>\) такие, что линейный многочлен записывается в виде
$$
x(\boldsymbol_<1>, \boldsymbol)+y(\boldsymbol_<2>, \boldsymbol)+z(\boldsymbol_<3>, \boldsymbol)-(\boldsymbol_<0>, \boldsymbol),\nonumber
$$
который совпадает с требуемым \((\boldsymbol-\boldsymbol_<0>, \boldsymbol)\).

Если система координат декартова прямоугольная, то вектор с компонентами \(A\), \(B\), \(C\) является нормальным вектором для плоскости с уравнением \(Ax+By+Cz+D = 0\).

Это сразу вытекает из формул \eqref и доказанного ранее утверждения о нахождении компонент в ортогональном базисе.

Любые два неколлинеарных вектора, удовлетворяющие уравнению \eqref, можно принять за направляющие векторы плоскости.

Утверждение 5 нетрудно доказать и непосредственно, рассматривая координаты вектора, параллельного плоскости, как разности соответствующих координат двух точек, лежащих в плоскости.

Все, сказанное о плоскостях, почти без изменений может быть сказано и о прямых на плоскости. В частности, верно следующее утверждение.

Действительно, \(\alpha_<1>, \alpha_<2>\), должны быть пропорциональны компонентам — \(B\), \(A\) направляющего вектора прямой.

Параллельность плоскостей и прямых на плоскости.

Ниже, говоря о параллельных прямых или плоскостях, мы будем считать, что параллельные плоскости (или прямые) не обязательно различны, то есть что плоскость (прямая) параллельна самой себе.

Прямые линии, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+C = 0,\ A_<1>x+B_<1>y+C_ <1>= 0,\nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число \(\lambda\), что
$$
A_ <1>= \lambda A,\ B_ <1>= \lambda B.\label
$$

Прямые совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнения \eqref выполнено (с тем же \(\lambda\)) равенство
$$
C_ <1>= \lambda C.\label
$$

Первая часть предложения прямо следует из того, что векторы с компонентами \((-B, A)\) и \((-B_<1>, A_<1>)\) — направляющие векторы прямых.

Докажем вторую часть. В равенствах \eqref и \eqref \(\lambda \neq 0\), так как коэффициенты в уравнении прямой одновременно нулю не равны. Поэтому, если эти равенства выполнены, уравнения эквивалентны и определяют одну и ту же прямую.

Обратно, пусть прямые параллельны. В силу первой части предложения их уравнения должны иметь вид \(Ax+By+C = 0\) и \(\lambda(Ax+By)+C_ <1>= 0\) при некотором \(\lambda\). Если, кроме того, существует общая точка \(M_<0>(x_<0>, y_<0>)\) обеих прямых, то \(Ax_<0>+By_<0>+C = 0\) и \(\lambda(Ax_<0>+By_<0>)+C_ <1>= 0\). Вычитая одно равенство из другого, получаем \(C_ <1>= \lambda C\), как и требовалось.

Плоскости, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+Cz+D = 0,\ A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0\nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число \(\lambda\), что
$$
A_ <1>= \lambda A,\ B_ <1>= \lambda B,\ C_ <1>= \lambda C.\label
$$

Плоскости совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнений \eqref выполнено (с тем же \(\lambda\)) равенство
$$
D_ <1>= \lambda D.\label
$$

Если плоскости параллельны, то их нормальные векторы \(\boldsymbol\) и \(\boldsymbol_<1>\) коллинеарны, и существует такое число \(\lambda\), что \(\boldsymbol_ <1>= \lambda\boldsymbol\). В силу уравнений \eqref \(A_ <1>= (\boldsymbol_<1>, \boldsymbol_<1>) = \lambda(\boldsymbol_<1>, \boldsymbol) = \lambda A\). Аналогично доказываются и остальные равенства \eqref. Обратно, если равенства \eqref выполнены, то из формулы \eqref следует, что \(\boldsymbol_ <1>= \lambda\boldsymbol\). Это доказывает первую часть предложения. Вторая его часть доказывается так же, как вторая часть предложения 7.

Условия \eqref выражают не что иное, как коллинеарность векторов с компонентами \((A, B)\) и \((A_<1>, B_<1>)\). Точно так же условия \eqref означают коллинеарность векторов с компонентами \((A, B, C)\) и \((A_<1>, B_<1>, C_<1>)\). Поэтому согласно ранее доказанным этому и этому утверждениям условие параллельности прямых на плоскости можно записать в виде
$$
\begin
A& B\\
A_<1>& B_<1>
\end
= 0,\label
$$
а условие параллельности плоскостей — в виде
$$
\begin
B& C\\
B_<1>& C_<1>
\end =
\begin
C& A\\
C_<1>& A_<1>
\end =
\begin
A& B\\
A_<1>& B_<1>
\end
= 0.\label
$$

Утверждению 7 можно придать чисто алгебраическую формулировку, если учесть, что координаты точки пересечения прямых — это решение системы, составленной из их уравнений.

При условии \eqref система линейных уравнений
$$
Ax+By+C = 0,\ A_<1>x+B_<1>y+C_ <1>= 0,\nonumber
$$
не имеет решений или имеет бесконечно много решений (в зависимости от \(C\) и \(C_<1>\). В последнем случае система равносильна одному из составляющих ее уравнений. Если же
$$
\begin
A& B\\
A_<1>& B_<1>
\end
\neq 0.\nonumber
$$
то при любых \(C\) и \(C_<1>\) система имеет единственное решение \((x, y)\).

Уравнения прямой в пространстве.

Прямая линия в пространстве может быть задана как пересечение двух плоскостей и, следовательно, в общей декартовой системе координат определяется системой уравнений вида
$$
\left\<\begin
Ax+By+Cz+D = 0,\\
A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0.
\end\right.\label
$$
Пересечение плоскостей — прямая линия тогда и только тогда, когда они не параллельны, что согласно \eqref означает, что хоть один из детерминантов отличен от нуля:
$$
\begin
B& C\\
B_<1>& C_<1>
\end^ <2>+
\begin
C& A\\
C_<1>& A_<1>
\end^ <2>+
\begin
A& B\\
A_<1>& B_<1>
\end^<2>
\neq 0.\label
$$

Разумеется, систему \eqref можно заменить на любую, ей эквивалентную. При этом прямая будет представлена как пересечение двух других проходящих через нее плоскостей.

Вспомним параметрические уравнения прямой \eqref. Допустим, что в них ни одна из компонент направляющего вектора не равна нулю. Тогда
$$
t = \frac><\alpha_<1>>,\ t = \frac><\alpha_<2>>,\ t = \frac><\alpha_<3>>,\nonumber
$$
и мы получаем два равенства
$$
\frac><\alpha_<2>> = \frac><\alpha_<3>>,\ \frac><\alpha_<1>> = \frac><\alpha_<3>>,\label
$$
или, в более симметричном виде,
$$
\frac><\alpha_<1>> = \frac><\alpha_<2>> = \frac><\alpha_<3>>,\label
$$
Уравнения \eqref представляют прямую как линию пересечения двух плоскостей, первая из которых параллельна оси абсцисс (в ее уравнение не входит переменная \(x\)), а вторая параллельна оси ординат.

Если обращается в нуль одна из компонент направляющего вектора, например, \(\alpha_<1>\), то уравнения прямой принимают вид
$$
x = x_<0>,\ \frac><\alpha_<2>> = \frac><\alpha_<3>>,\label
$$
Эта прямая лежит в плоскости \(x = x_<0>\) и, следовательно, параллельна плоскости \(x = 0\). Аналогично пишутся уравнения прямой, если в нуль обращается не \(\alpha_<1>\), а другая компонента.

Когда равны нулю две компоненты направляющего вектора, например, \(\alpha_<1>\) и \(\alpha_<2>\), то прямая имеет уравнения
$$
x = x_<0>,\ y = y_<0>.\label
$$
Такая прямая параллельна одной из осей координат, в нашем случае — оси аппликат.

Важно уметь находить начальную точку и направляющий вектор прямой, заданной системой линейных уравнений \eqref. По условию \eqref один из детерминантов отличен от нуля. Допустим для определенности, что \(AB_<1>-A_<1>B \neq 0\). В силу утверждения 9 при любом фиксированном \(z\) система уравнений будет иметь единственное решение \((x, y)\), в котором \(x\) и \(y\), разумеется, зависят от \(z\). Они — линейные многочлены от \(z\): \(x = \alpha_<1>z+\beta_<1>\), \(y = \alpha_<2>z+\beta_<2>\).

Не будем доказывать этого, хотя это и не трудно сделать. Для ясности, заменяя \(z\) на \(t\), получаем параметрические уравнения прямой
$$
x = \alpha_<1>t+\beta_<1>,\ y = \alpha_<2>t+\beta_<2>,\ z = t.\nonumber
$$

Первые две координаты начальной точки прямой \(M_<0>(\beta_<1>, \beta_<2>, 0)\) можно получить, решая систему \eqref при значении \(z = 0\).

Из параметрических уравнений видно, что в этом случае направляющий вектор имеет координаты \((\alpha_<1>, \alpha_<2>, 1)\). Найдем его компоненты в общем виде. Если система координат декартова прямоугольная, векторы с компонентами \((A, B, C)\) и \(A_<1>, B_<1>, C_<1>\) перпендикулярны соответствующим плоскостям, а потому их векторное произведение параллельно прямой \eqref, по которой плоскости пересекаются. Вычисляя векторное произведение в ортонормированном базисе, мы получаем компоненты направляющего вектора
$$
\begin
B& C\\
B_<1>& C_<1>
\end,\
\begin
C& A\\
C_<1>& A_<1>
\end,\
\begin
A& B\\
A_<1>& B_<1>
\end.\label
$$

Вектор с компонентами \eqref есть направляющий вектор прямой с уравнениями \eqref, какова бы ни была декартова система координат.

Согласно утверждению 5 каждый ненулевой вектор, компоненты которого \((\alpha_<1>, \alpha_<2>, \alpha_<3>)\) удовлетворяют уравнению \(A\alpha_<1>+B\alpha_<2>+C\alpha_ <3>= 0\), параллелен плоскости с уравнением \(Ax+By+Cz+D = 0\). Если, кроме того, он удовлетворяет уравнению \(A_<1>\alpha_<1>+B_<1>\alpha_<2>+C_<1>\alpha_ <3>= 0\), то он параллелен и второй плоскости, то есть может быть принят за направляющий вектор прямой. Вектор с компонентами \eqref ненулевой в силу неравенства \eqref. Непосредственно легко проверить, что его компоненты удовлетворяют обоим написанным выше условиям. На этом доказательство заканчивается.

Уравнение плоскости: как составить? Виды уравнений плоскости

В пространстве плоскость можно задавать разными способами (одной точкой и вектором, двумя точками и вектором, тремя точками и др.). Именно с учетом этого уравнение плоскости может иметь различные виды. Также при соблюдении определенных условий плоскости могут быть параллельными, перпендикулярными, пересекающимися и т.д. Об этом и поговорим в данной статье. Мы научимся составлять общее уравнение плоскости и не только.

Нормальный вид уравнения

Допустим, есть пространство R₃, которое имеет прямоугольную координатную систему XYZ. Зададим вектор α, который будет выпущен из начальной точки О. Через конец вектора α проведем плоскость П, которая будет ему перпендикулярна.

Обозначим на П произвольную точку Q=(х,у,z). Радиус-вектор точки Q подпишем буквой р. При этом длина вектора α равняется р=IαI и Ʋ=(cosα,cosβ,cosγ).

Это единичный вектор, который направлен в сторону, как и вектор α. α, β и γ – это углы, которые образуются между вектором Ʋ и положительными направлениями осей пространства х, у, z соответственно. Проекция какой-либо точки QϵП на вектор Ʋ является постоянной величиной, которая равна р: (р,Ʋ) = р(р≥0).

Указанное уравнение имеет смысл, когда р=0. Единственное, плоскость П в этом случае будет пересекать точку О (α=0), которая является началом координат, и единичный вектор Ʋ, выпущенный из точки О, будет перпендикулярен к П, несмотря на его направление, что означает, что вектор Ʋ определяется с точностью до знака. Предыдущее уравнение является уравнением нашей плоскости П, выраженным в векторной форме. А вот в координатах его вид будет таким:

Р здесь больше или равно 0. Мы нашли уравнение плоскости в пространстве в нормальном виде.

Общее уравнение

Если уравнение в координатах умножим на любое число, которое не равно нулю, получим уравнение, эквивалентное данному, определяющее ту самую плоскость. Оно будет иметь такой вид:

Здесь А, В, С – это числа, одновременно отличные от нуля. Это уравнение именуется как уравнение плоскости общего вида.

Уравнения плоскостей. Частные случаи

Уравнение в общем виде может видоизменяться при наличии дополнительных условий. Рассмотрим некоторые из них.

Предположим, что коэффициент А равен 0. Это означает, что данная плоскость параллельна заданной оси Ох. В этом случае вид уравнения изменится: Ву+Cz+D=0.

Аналогично вид уравнения будет изменяться и при следующих условиях:

• Во-первых, если В=0, то уравнение изменится на Ах+Cz+D=0, что будет свидетельствовать о параллельности к оси Оу.
• Во-вторых, если С=0, то уравнение преобразуется в Ах+Ву+D=0, что будет говорить о параллельности к заданной оси Oz.
• В-третьих, если D=0, уравнение будет выглядеть как Ах+Ву+Cz=0, что будет означать, что плоскость пересекает О (начало координат).
• В-четвертых, если A=B=0, то уравнение изменится на Cz+D=0, что будет доказывать параллельность к Oxy.
• В-пятых, если B=C=0, то уравнение станет Ах+D=0, а это означает, что плоскость к Oyz параллельна.
• В-шестых, если A=C=0, то уравнение приобретет вид Ву+D=0, то есть будет сообщать о параллельности к Oxz.

Вид уравнения в отрезках

В случае когда числа А, В, С, D отличны от нуля, вид уравнения (0) может быть следующим:

в котором а = -D/А, b = -D/В, с = -D/С.

Получаем в итоге уравнение плоскости в отрезках. Стоит отметить, что данная плоскость будет пересекать ось Ох в точке с координатами (а,0,0), Оу – (0,b,0), а Oz – (0,0,с).

С учетом уравнения х/а + у/b + z/с = 1 нетрудно визуально представить размещение плоскости относительно заданной координатной системы.

Координаты нормального вектора

Нормальный вектор n к плоскости П имеет координаты, которые являются коэффициентами общего уравнения данной плоскости, то есть n (А,В,С).

Для того чтобы определить координаты нормали n, достаточно знать общее уравнение заданной плоскости.

При использовании уравнения в отрезках, которое имеет вид х/а + у/b + z/с = 1, как и при использовании общего уравнения, можно записать координаты любого нормального вектора заданной плоскости: (1/а + 1/b + 1/с).

Стоит отметить, что нормальный вектор помогает решить разнообразные задачи. К самым распространенным относятся задачи, заключающиеся в доказательстве перпендикулярности или параллельности плоскостей, задачи по нахождению углов между плоскостями или углов между плоскостями и прямыми.

Вид уравнения плоскости согласно координатам точки и нормального вектора

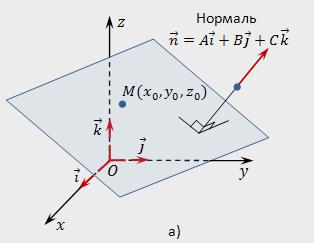
Ненулевой вектор n, перпендикулярный заданной плоскости, называют нормальным (нормалью) для заданной плоскости.

Предположим, что в координатном пространстве (прямоугольной координатной системе) Oxyz заданы:

• точка Мₒ с координатами (хₒ,уₒ,zₒ);
• нулевой вектор n=А*i+В*j+С*k.

Нужно составить уравнение плоскости, которая будет проходить через точку Мₒ перпендикулярно нормали n.

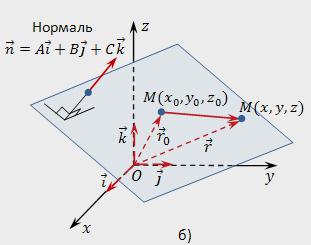
В пространстве выберем любую произвольную точку и обозначим ее М (х у,z). Пускай радиус-вектор всякой точки М (х,у,z) будет r=х*i+у*j+z*k, а радиус-вектор точки Мₒ (хₒ,уₒ,zₒ) – rₒ=хₒ*i+уₒ*j+zₒ*k. Точка М будет принадлежать заданной плоскости, если вектор МₒМ будет перпендикулярен вектору n. Запишем условие ортогональности при помощи скалярного произведения:

Поскольку МₒМ = r–rₒ, векторное уравнение плоскости выглядеть будет так:

Данное уравнение может иметь и другую форму. Для этого используются свойства скалярного произведения, а преобразовывается левая сторона уравнения. [r – rₒ, n] = [r, n] – [rₒ, n]. Если [rₒ, n] обозначить как с, то получится следующее уравнение: [r, n] – с = 0 или [r, n] = с, которое выражает постоянство проекций на нормальный вектор радиус-векторов заданных точек, которые принадлежат плоскости.

Теперь можно получить координатный вид записи векторного уравнения нашей плоскости [r – rₒ, n] = 0. Поскольку r–rₒ = (х–хₒ)*i + (у–уₒ)*j + (z–zₒ)*k, а n = А*i+В*j+С*k, мы имеем:

Выходит, у нас образовывается уравнение плоскости, проходящей через точку перпендикулярно нормали n:

Вид уравнения плоскости согласно координатам двух точек и вектора, коллинеарного плоскости

Зададим две произвольные точки М′ (х′,у′,z′) и М″ (х″,у″,z″), а также вектор а (а′,а″,а‴).

Теперь мы сможем составить уравнение заданной плоскости, которая будет проходить через имеющиеся точки М′ и М″, а также всякую точку М с координатами (х,у,z) параллельно заданному вектору а.

При этом векторы М′М= <х-х′;у-у′;z-z′>и М″М= <х″-х′;у″-у′;z″-z′>должны быть компланарными с вектором а=(а′,а″,а‴), а это значит, что (М′М, М″М, а)=0.

Итак, наше уравнение плоскости в пространстве будет выглядеть так:

Вид уравнения плоскости, пересекающей три точки

Допустим, у нас есть три точки: (х′,у′,z′), (х″,у″,z″), (х‴,у‴,z‴), которые не принадлежат одной прямой. Необходимо написать уравнение плоскости, проходящей через заданные три точки. Теория геометрии утверждает, что такого рода плоскость действительно существует, вот только она единственная и неповторимая. Поскольку эта плоскость пересекает точку (х′,у′,z′), вид ее уравнения будет следующим:

Здесь А, В, С отличные от нуля одновременно. Также заданная плоскость пересекает еще две точки: (х″,у″,z″) и (х‴,у‴,z‴). В связи с этим должны выполняться такого рода условия:

Сейчас мы можем составить однородную систему уравнений (линейную) с неизвестными u, v, w:

В нашем случае х,у или z выступает произвольной точкой, которая удовлетворяет уравнение (1). Учитывая уравнение (1) и систему из уравнений (2) и (3), системе уравнений, указанной на рисунке выше, удовлетворяет вектор N (А,В,С), который является нетривиальным. Именно потому определитель данной системы равняется нулю.

Уравнение (1), которое у нас получилось, это и есть уравнение плоскости. Через 3 точки она точно проходит, и это легко проверить. Для этого нужно разложить наш определитель по элементам, находящимся в первой строке. Из существующих свойств определителя вытекает, что наша плоскость одновременно пересекает три изначально заданные точки (х′,у′,z′), (х″,у″,z″), (х‴,у‴,z‴). То есть мы решили поставленную перед нами задачу.

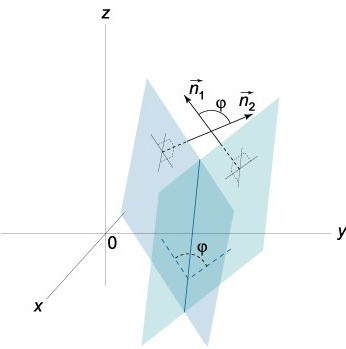
Двухгранный угол между плоскостями

Двухгранный угол представляет собой пространственную геометрическую фигуру, образованную двумя полуплоскостями, которые исходят из одной прямой. Иными словами, это часть пространства, которая ограничивается данными полуплоскостями.

Допустим, у нас имеются две плоскости со следующими уравнениями:

Нам известно, что векторы N=(А,В,С) и N¹=(А¹,В¹,С¹) перпендикулярны согласно заданным плоскостям. В связи с этим угол φ меж векторами N и N¹ равняется углу (двухгранному), который находится между этими плоскостями. Скалярное произведение имеет вид:

Достаточно учесть, что 0≤φ≤π.

На самом деле две плоскости, которые пересекаются, образуют два угла (двухгранных): φ₁ и φ₂. Сумма их равна π (φ₁+ φ₂= π). Что касается их косинусов, то их абсолютные величины равны, но различаются они знаками, то есть cos φ₁=-cos φ₂. Если в уравнении (0) заменить А, В и С на числа -А, -В и -С соответственно, то уравнение, которое мы получим, будет определять эту же плоскость, единственное, угол φ в уравнении cos φ= NN 1 /|N||N 1 | будет заменен на π-φ.

Уравнение перпендикулярной плоскости

Перпендикулярными называются плоскости, между которыми угол равен 90 градусов. Используя материал, изложенный выше, мы можем найти уравнение плоскости, перпендикулярной другой. Допустим, у нас имеются две плоскости: Ах+Ву+Cz+D=0 и А¹х+В¹у+С¹z+D=0. Мы можем утверждать, что перпендикулярными они будут, если cosφ=0. Это значит, что NN¹=АА¹+ВВ¹+СС¹=0.

Уравнение параллельной плоскости

Параллельными называются две плоскости, которые не содержат общих точек.

Условие параллельности плоскостей (их уравнения те же, что и в предыдущем пункте) заключается в том, что векторы N и N¹, которые к ним перпендикулярны, коллинеарные. А это значит, что выполняются следующие условия пропорциональности:

Если условия пропорциональности являются расширенными — А/А¹=В/В¹=С/С¹=DD¹,

это свидетельствует о том, что данные плоскости совпадают. А это значит, что уравнения Ах+Ву+Cz+D=0 и А¹х+В¹у+С¹z+D¹=0 описывают одну плоскость.

Расстояние до плоскости от точки

Допустим, у нас есть плоскость П, которая задана уравнением (0). Необходимо найти до нее расстояние от точки с координатами (хₒ,уₒ,zₒ)=Qₒ. Чтобы это сделать, нужно привести уравнение плоскости П в нормальный вид:

В данном случае ρ (х,у,z) является радиус-вектором нашей точки Q, расположенной на П, р – это длина перпендикуляра П, который был выпущен из нулевой точки, v – это единичный вектор, который расположен в направлении а.

Разница ρ-ρº радиус-вектора какой-нибудь точки Q=(х,у,z), принадлежащий П, а также радиус-вектора заданной точки Q₀=(хₒ,уₒ,zₒ) является таким вектором, абсолютная величина проекции которого на v равняется расстоянию d, которое нужно найти от Q₀=(хₒ,уₒ,zₒ) до П:

(ρ-ρ 0 ,v)= (ρ,v)–(ρ 0 ,v) =р–(ρ 0 ,v).

Вот и получается,

Теперь видно, чтобы рассчитать расстояние d от Q₀ до плоскости П, нужно использовать нормальный вид уравнения плоскости, при этом перенести в левую часть р, а в последнюю вместо х,у,z подставить (хₒ,уₒ,zₒ).

Таким образом, мы найдем абсолютное значение полученного выражения, то есть искомое d.

Используя язык параметров, получаем очевидное:

Если заданная точка Q₀ находится по другую сторону от плоскости П, как и начало координат, то между вектором ρ-ρ 0 и v находится тупой угол, следовательно:

В случае когда точка Q₀ совместно с началом координат располагается по одну и ту же сторону от П, то создаваемый угол острый, то есть:

d=(ρ-ρ 0 ,v)=р — (ρ 0 , v)>0.

В итоге получается, что в первом случае (ρ 0 ,v)>р, во втором (ρ 0 ,v) 2 сентября, 2014