Уравнение плоскости через смешанное произведение

Уравнение плоскости, которая проходит через три заданные точки, не лежащие на одной прямой

В рамках этого материала мы разберем, как найти уравнение плоскости, если мы знаем координаты трех различных ее точек, которые не лежат на одной прямой. Для этого нам понадобится вспомнить, что такое прямоугольная система координат в трехмерном пространстве. Для начала мы введем основной принцип данного уравнения и покажем, как именно использовать его при решении конкретных задач.

Как найти уравнение плоскости, которая проходит через 3 заданные точки

Для начала нам необходимо вспомнить одну аксиому, которая звучит следующим образом:

Если три точки не совпадают друг с другом и не лежат на одной прямой, то в трехмерном пространстве через них проходит только одна плоскость.

Иными словами, если у нас есть три разных точки, координаты которых не совпадают и которые нельзя соединить прямой, то мы можем определить плоскость, проходящую через нее.

Допустим, у нас имеется прямоугольная система координат. Обозначим ее O x y z . В ней лежат три точки M с координатами M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) , которые нельзя соединить прямой линией. Исходя из этих условий, мы можем записать уравнение необходимой нам плоскости. Есть два подхода к решению этой задачи.

1. Первый подход использует общее уравнение плоскости. В буквенном виде оно записывается как A ( x — x 1 ) + B ( y — y 1 ) + C ( z — z 1 ) = 0 . С его помощью можно задать в прямоугольной системе координат некую плоскость альфа, которая проходит через первую заданную точку M 1 ( x 1 , y 1 , z 1 ) . У нас получается, что нормальный вектор плоскости α будет иметь координаты A , B , C .

Зная координаты нормального вектора и координаты точки, через которую проходит плоскость, мы можем записать общее уравнение этой плоскости.

Из этого мы и будем исходить в дальнейшем.

Таким образом, согласно условиям задачи, мы имеем координаты искомой точки (даже трех), через которую проходит плоскость. Чтобы найти уравнение, нужно вычислить координаты ее нормального вектора. Обозначим его n → .

Вспомним правило: любой не равный нулю вектор данной плоскости является перпендикулярным нормальному вектору этой же плоскости. Тогда мы имеем, что n → будет перпендикулярным по отношению к векторам, составленным из исходных точек M 1 M 2 → и M 1 M 3 → . Тогда мы можем обозначить n → как векторное произведение вида M 1 M 2 → · M 1 M 3 → .

Поскольку M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) а M 1 M 3 → = x 3 — x 1 , y 3 — y 1 , z 3 — z 1 (доказательства этих равенств приведены в статье, посвященной вычислению координат вектора по координатам точек), тогда получается, что:

n → = M 1 M 2 → × M 1 M 3 → = i → j → k → x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1

Если мы вычислим определитель, то получим необходимые нам координаты нормального вектора n → . Теперь мы можем записать нужное нам уравнение плоскости, проходящей через три заданные точки.

2. Второй подход нахождения уравнения, проходящей через M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) , основан на таком понятии, как компланарность векторов.

Если у нас есть множество точек M ( x , y , z ) , то в прямоугольной системе координат они определяют плоскость для заданных точек M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) только в том случае, когда векторы M 1 M → = ( x — x 1 , y — y 1 , z — z 1 ) , M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) и M 1 M 3 → = ( x 3 — x 1 , y 3 — y 1 , z 3 — z 1 ) будут компланарными.

На схеме это будет выглядеть так:

Это будет означать, что смешанное произведение векторов M 1 M → , M 1 M 2 → , M 1 M 3 → будет равно нулю: M 1 M → · M 1 M 2 → · M 1 M 3 → = 0 , поскольку это является основным условием компланарности: M 1 M → = ( x — x 1 , y — y 1 , z — z 1 ) , M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) и M 1 M 3 → = ( x 3 — x 1 , y 3 — y 1 , z 3 — z 1 ) .

Запишем полученное уравнение в координатной форме:

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0

После того, как мы вычислим определитель, мы сможем получить нужное нам уравнение плоскости для трех не лежащих на одной прямой точек M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) .

От полученного в результате уравнения можно перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости, если этого требуют условия задачи.

В следующем пункте мы приведем примеры того, как указанные нами подходы реализуются на практике.

Примеры задач на составление уравнения плоскости, проходящих через 3 точки

Ранее мы выделили два подхода, с помощью которых можно найти искомое уравнение. Давайте посмотрим, как они применяются в решениях задач и когда следует выбирать каждый из них.

Есть три точки, не лежащие на одной прямой, с координатами M 1 ( — 3 , 2 , — 1 ) , M 2 ( — 1 , 2 , 4 ) , M 3 ( 3 , 3 , — 1 ) . Составьте уравнение плоскости, проходящей через них.

Решение

Используем поочередно оба способа.

1. Найдем координаты двух нужных нам векторов M 1 M 2 → , M 1 M 3 → :

M 1 M 2 → = — 1 — — 3 , 2 — 2 , 4 — — 1 ⇔ M 1 M 2 → = ( 2 , 0 , 5 ) M 1 M 3 → = 3 — — 3 , 3 — 2 , — 1 — — 1 ⇔ M 1 M 3 → = 6 , 1 , 0

Теперь вычислим их векторное произведение. Вычисления определителя расписывать при этом не будем:

n → = M 1 M 2 → × M 1 M 3 → = i → j → k → 2 0 5 6 1 0 = — 5 · i → + 30 · j → + 2 · k →

У нас получился нормальный вектор плоскости, которая проходит через три искомые точки: n → = ( — 5 , 30 , 2 ) . Далее нам нужно взять одну из точек, например, M 1 ( — 3 , 2 , — 1 ) , и записать уравнение для плоскости с вектором n → = ( — 5 , 30 , 2 ) . Мы получим, что: — 5 · ( x — ( — 3 ) ) + 30 · ( y — 2 ) + 2 · ( z — ( — 1 ) ) = 0 ⇔ — 5 x + 30 y + 2 z — 73 = 0

Это и есть нужное нам уравнение плоскости, которая проходит через три точки.

2. Используем другой подход. Запишем уравнение для плоскости с тремя точками M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) в следующем виде:

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0

Сюда можно подставить данные из условия задачи. Поскольку x 1 = — 3 , y 1 = 2 , z 1 = — 1 , x 2 = — 1 , y 2 = 2 , z 2 = 4 , x 3 = 3 , y 3 = 3 , z 3 = — 1 , в итоге мы получим:

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = x — ( — 3 ) y — 2 z — ( — 1 ) — 1 — ( — 3 ) 2 — 2 4 — ( — 1 ) 3 — ( — 3 ) 3 — 2 — 1 — ( — 1 ) = = x + 3 y — 2 z + 1 2 0 5 6 1 0 = — 5 x + 30 y + 2 z — 73

Мы получили нужное нам уравнение.

Ответ: — 5 x + 30 y + 2 z — 73 .

А как быть, если заданные точки все же лежат на одной прямой и нам нужно составить уравнение плоскости для них? Здесь сразу надо сказать, что это условие будет не совсем корректным. Через такие точки может проходить бесконечно много плоскостей, поэтому вычислить один-единственный ответ невозможно. Рассмотрим такую задачу, чтобы доказать некорректность подобной постановки вопроса.

У нас есть прямоугольная система координат в трехмерном пространстве, в которой размещены три точки с координатами M 1 ( 5 , — 8 , — 2 ) , M 2 ( 1 , — 2 , 0 ) , M 3 ( — 1 , 1 , 1 ) . Необходимо составить уравнение плоскости, проходящей через нее.

Решение

Используем первый способ и начнем с вычисления координат двух векторов M 1 M 2 → и M 1 M 3 → . Подсчитаем их координаты: M 1 M 2 → = ( — 4 , 6 , 2 ) , M 1 M 3 → = — 6 , 9 , 3 .

Векторное произведение будет равно:

M 1 M 2 → × M 1 M 3 → = i → j → k → — 4 6 2 — 6 9 3 = 0 · i ⇀ + 0 · j → + 0 · k → = 0 →

Поскольку M 1 M 2 → × M 1 M 3 → = 0 → , то наши векторы будут коллинеарными (перечитайте статью о них, если забыли определение этого понятия). Таким образом, исходные точки M 1 ( 5 , — 8 , — 2 ) , M 2 ( 1 , — 2 , 0 ) , M 3 ( — 1 , 1 , 1 ) находятся на одной прямой, и наша задача имеет бесконечно много вариантов ответа.

Если мы используем второй способ, у нас получится:

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0 ⇔ x — 5 y — ( — 8 ) z — ( — 2 ) 1 — 5 — 2 — ( — 8 ) 0 — ( — 2 ) — 1 — 5 1 — ( — 8 ) 1 — ( — 2 ) = 0 ⇔ ⇔ x — 5 y + 8 z + 2 — 4 6 2 — 6 9 3 = 0 ⇔ 0 ≡ 0

Из получившегося равенства также следует, что заданные точки M 1 ( 5 , — 8 , — 2 ) , M 2 ( 1 , — 2 , 0 ) , M 3 ( — 1 , 1 , 1 ) находятся на одной прямой.

Если вы хотите найти хоть один ответ этой задачи из бесконечного множества ее вариантов, то нужно выполнить следующие шаги:

1. Записать уравнение прямой М 1 М 2 , М 1 М 3 или М 2 М 3 (при необходимости посмотрите материал об этом действии).

2. Взять точку M 4 ( x 4 , y 4 , z 4 ) , которая не лежит на прямой М 1 М 2 .

3. Записать уравнение плоскости, которая проходит через три различных точки М 1 , М 2 и M 4 , не лежащих на одной прямой.

Уравнение плоскости через 3 точки

Вы будете перенаправлены на Автор24

Для начала стоит напомнить, как выглядит общее уравнение плоскости:

$Ax \cdot + By + Cz + D = 0\left(1\right)$,

при этом: $\$ — координаты нормального вектора данной плоскости, а $D$ — свободный член.

В общем уравнении коэффициенты $A, B, C$ не могут быть одновременно равны нулю, если же один из коэффициентов нулевой — уравнение называется неполным. При $D=0$ плоскость проходит через центр осей координат.

Также в дальнейшем нам пригодится уравнение плоскости, заданной точкой, лежащей в данной плоскости и нормальным вектором:

здесь $(x_0; y_0; z_0)$ — координаты точки плоскости.

Теперь непосредственно к делу.

Уравнение плоскости через три точки можно выразить несколькими способами: с помощью смешанного произведения векторов и выразив сначала нормальный вектор плоскости и используя одну точку.

Уравнение плоскости, проходящей через 3 точки, через смешанное произведение векторов

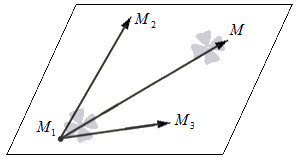
Рассмотрим три точки $M_1, M_2, M_3$, не находящиеся на одной прямой. Соответственно аксиоме стереометрии о том, что три точки задают плоскость, и притом только одну, все эти точки лежат в одной плоскости $α$.

Рисунок 1. Плоскость через 3 точки. Автор24 — интернет-биржа студенческих работ

Рассмотрим точку $M$, лежащую в плоскости $α$. Если описать плоскость $α$ как множество точек $M$, вектора $\vec$, $\vec$ и $\vec$ должны быть компланарны между собой. А как известно, вектора компланарны между собой если их смешанное произведение равно нулю.

Соответственно, для того чтобы вычислить это смешанное произведение, необходимо вычислить определитель третьего порядка, каждая строка которого является координатами вышеперечисленных векторов.

Готовые работы на аналогичную тему

Пусть координаты точек $M, M_1, M_2, M_3$ — $(x; y; z), (x_1;y_1; z_1), (x_2;y_2; z_2), (x_3;y_3;z_3)$ соответственно. Тогда координаты каждого из вышеперечисленных векторов составят:

Составим определитель, описывающий смешанное произведение векторов:

$\begin <|ccc|>x-x_1 && y-y_1 && z-z_1 \\ x_2-x_1 && y_2-y_1 && z_2-z_1 \\ x_3-x_1 && y_3-y_1 &&z_3-z_1 \\ \end=0$ — уравнение плоскости через 3 точки.

При вычислении этого определителя получается общее уравнение плоскости, проходящей через три точки. Это можно увидеть, раскрыв определитель по первой строке:

$\begin <|cc|>y_2-y_1 && z_2-z_1 \\ y_3-y_1 &&z_3-z_1 \\ \end \cdot ( x-x_1) + \begin <|cc|>x_2-x_1 && z_2-z_1 \\ x_3-x_1 &&z_3-z_1 \\ \end \cdot (y-y_1) + \begin <|cc|>x_2-x_1 && y_2-y_1 \\ x_3-x_1 && y_3-y_1 \\ \end \cdot (z-z_1) = 0\left(3\right)$.

Коэффициенты из уравнения $(3)$ также совпадают с координатами векторного произведения $\vec×\vec$ и, так как два этих вектора неколлинеарны и параллельны рассматриваемой плоскости $α$, данное векторное произведение представляет собой нормальный вектор к плоскости, для которой составляется уравнение.

Уравнение плоскости, заданной 3 точками, через нормальный вектор и точку

Другим альтернативным методом задания плоскости является использование нормального вектора плоскости и точки, принадлежащей данной плоскости.

Для того чтобы воспользоваться данным методом, найдём векторное произведение векторов $\vec$ и $\vec$:

$[\vec × \vec]= \begin <|ccc|>\vec &&\vec &&\vec \\ x_2-x_1 &&y_2-y_1 &&z_2-z_1 \\ x_3-x_1 &&y_3-y_1 &&z_3-z_1 \\ \end=0$.

Данное произведение является нормальным вектором плоскости, для которой составляется уравнение. Полученные координаты нормального вектора можно использовать непосредственно для составления уравнения плоскости.

Зная точку, принадлежащую этой плоскости, можно подставить координаты нормального вектора и координаты точки в уравнение $(2)$ и получить уравнение плоскости:

В этом уравнении $n_x; n_y; n_z$ — координаты нормального вектора, определённого из векторного произведения векторов $\vec$ и $\vec$, а $(x_3; y_3; z_3)$ — некая точка, принадлежащая данной плоскости.

По сути, два вышеприведённых метода представляют одно и то же, так как в обоих необходимо найти координаты нормального вектора и затем, используя их и координаты третьей неиспользованной точки, получить уравнение самой плоскости.

К данной задаче можно также свести задачу с нахождением уравнения плоскости по уравнениям лежащих в ней параллельных и пересекающихся прямых.

Cоставить уравнение плоскости, проходящей через 3 точки $M_1,M_2, M_3$ c координатами $(1;2;3), (1;2;4)$ и $(4;2;-1)$ соответственно.

Воспользуемся вторым способом и найдём координаты вектора через векторное произведение. Для этого сначала выразим координаты векторов:

Найдём их векторное произведение:

Подставим координаты нормального вектора в уравнение $(2)$:

$0\cdot(x-4)+(-3) \cdot (y-2)+0 \cdot(z+1)=0$.

$-3y+6=0$ — искомое уравнение плоскости.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 14 03 2021

Уравнение плоскости через смешанное произведение

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЕХ ВЕКТОРОВ И ЕГО СВОЙСТВА

Смешанным произведением трёх векторов называют число, равное . Обозначается . Здесь первые два вектора умножаются векторно и затем полученный вектор умножается скалярно на третий вектор . Очевидно, такое произведение есть некоторое число.

Рассмотрим свойства смешанного произведения.

1. Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е. .

Таким образом, и .

Доказательство. Отложим векторы от общего начала и построим на них параллелепипед. Обозначим и заметим, что . По определению скалярного произведения

. Предполагая, что и обозначив через h высоту параллелепипеда, находим .

Таким образом, при

Если же , то и . Следовательно, .

Объединяя оба эти случая, получаем или .

Из доказательства этого свойства в частности следует, что если тройка векторов правая, то смешанное произведение , а если – левая, то .

Для любых векторов , , справедливо равенство

.

Доказательство этого свойства следует из свойства 1. Действительно, легко показать, что и . Причём знаки «+» и «–» берутся одновременно, т.к. углы между векторами и и и одновременно острые или тупые.

При перестановке любых двух сомножителей смешанное произведение меняет знак.

Действительно, если рассмотрим смешанное произведение , то, например, или

.

Смешанное произведение тогда и только тогда, когда один из сомножителей равен нулю или векторы – компланарны.

Предположим, что , т.е. , тогда или или .

Если , то или или . Поэтому – компланарны.

Если , то , , — компланарны.

Пусть векторы – компланарны и α – плоскость, которой они параллельны , т. е. и . Тогда , а значит , поэтому или .

Т.о., необходимым и достаточным условием компланарности 3-х векторов является равенство нулю их смешанного произведения. Кроме того, отсюда следует, что три вектора образуют базис в пространстве, если .

Если векторы заданы в координатной форме , то можно показать, что их смешанное произведение находится по формуле:

.

Т. о., смешанное произведение равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора.

Показать, что векторы образуют базис в пространстве.

, т.е. векторы – базис.

Найти объём пирамиды с вершинами в точках A(2; -2; 0), B(-1; 4; -4), C(4; -8; 5), D(1; -7; 0). Правую или левую тройку образуют векторы и ?

Т. к. , то тройка векторов левая.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

Уравнение F(x, y, z) = 0 определяет в пространстве Oxyz некоторую поверхность, т.е. геометрическое место точек, координаты которых x, y, z удовлетворяют этому уравнению. Это уравнение называется уравнением поверхности, а x, y, z – текущими координатами.

Однако, часто поверхность задаётся не уравнением, а как множество точек пространства, обладающих тем или иным свойством. В этом случае требуется найти уравнение поверхности, исходя из её геометрических свойств.

НОРМАЛЬНЫЙ ВЕКТОР ПЛОСКОСТИ.

УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДАННУЮ ТОЧКУ

Рассмотрим в пространстве произвольную плоскостьσ. Её положение определяется заданием вектора , перпендикулярного этой плоскости, и некоторой фиксированной точки M₀(x₀, y₀, z₀), лежащей в плоскости σ.

Вектор перпендикулярный плоскости σ, называется нормальным вектором этой плоскости. Пусть вектор имеет координаты .

Выведем уравнение плоскости σ, проходящей через данную точку M₀ и имеющей нормальный вектор . Для этого возьмём на плоскости σ произвольную точку M(x, y, z) и рассмотрим вектор .

Для любой точки M Î σ вектор .Поэтому их скалярное произведение равно нулю . Это равенство – условие того, что точка M Î σ. Оно справедливо для всех точек этой плоскости и нарушается, как только точка M окажется вне плоскости σ.

Если обозначить через радиус-вектор точки M, – радиус-вектор точкиM₀, то и уравнение можно записать в виде

.

Это уравнение называется векторным уравнением плоскости. Запишем его в координатной форме. Так как , то

.

Итак, мы получили уравнение плоскости, проходящей через данную точку. Таким образом, для того чтобы составить уравнение плоскости, нужно знать координаты нормального вектора и координаты некоторой точки, лежащей на плоскости.

Заметим, что уравнение плоскости является уравнением 1-ой степени относительно текущих координат x, y и z.

Составить уравнение плоскости, проходящей через точку М(1;-2;3) перпендикулярно вектору .

Используя выведенное уравнение, получим 2(x-1)+0(y+2)+4(z-3)=0 или x+2z-7=0.

Составить уравнение плоскости, проходящей через точки A(1;2;3), B(-1;0;0), C(3;0;1).

Чтобы составить требуемое уравнение, нужно найти вектор перпендикулярный плоскости. Заметим, что таким вектором будет вектор . Найдем это вектор. . Тогда

.

Взяв в качестве точки, через которую проходит плоскость точку A, получим уравнение –2(x-1)-10(y-2)+8(z-3)=0 или x+5y-4z+1=0.

ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ

Можно показать, что любое уравнение первой степени относительно декартовых координат x, y, z представляет собой уравнение некоторой плоскости. Это уравнение записывается в виде:

и называется общим уравнением плоскости, причём координаты A, B, C здесь являются координатами нормального вектора плоскости.

Рассмотрим частные случаи общего уравнения. Выясним, как располагается плоскость относительно системы координат, если один или несколько коэффициентов уравнения обращаются в ноль.

Свободный член равен нулю D= 0.

В этом случае уравнение плоскости принимает вид Ax+Cy+Bz=0. Т.к. числа x=0, y=0, z=0 удовлетворяют уравнению плоскости, то она проходит через начало координат.

Один из коэффициентов при текущих координатах равен нулю. Пусть например A =0. В этом случае уравнение плоскости имеет вид By+Cz+D=0. Нормальный вектор плоскости имеет координаты и перпендикулярен оси Ox. Следовательно, плоскость параллельна оси Ox.

Аналогично, если B= 0, то плоскость параллельна оси Oy и C= 0 – плоскость параллельна оси Oz.

Т.о., если в уравнении плоскости один из коэффициентов при текущей координате равен нулю, то плоскость параллельна соответствующей координатной оси.

Коэффициент при текущей координате и свободный член равны нулю. Например, A = D = 0. В этом случае уравнению By + Cz = 0 соответствует плоскость, проходящая через начало координат (согласно п.1). Кроме того, учитывая п.2, данная плоскость должна быть параллельна оси Ox. Следовательно, плоскость проходит через ось Ox.

Аналогично, при B=D=0 плоскость Ax+Cz=0 проходит через ось Oy. При C=D=0 плоскость проходит через ось Oz.

Два коэффициента при текущих координатах раны нулю. Пусть, например, A=B=0. Тогда плоскость Cz+D=0 в силу п.2 будет параллельна осям Ox и Oy, а следовательно параллельна координатной плоскости xOy.

Аналогично, уравнениям Ax+D=0 и By+D=0 соответствуют плоскости, параллельные координатным плоскостям yOz и xOz.

Составить уравнение плоскости, проходящей параллельно оси Oy, через точки M₁(1; 0; -1), M₂(-1; 2;0).

Так как ось Oy параллельна , то уравнение плоскости Ax+Cy+D=0. Учитывая, что M₁ Î α, M₂ Î α, подставим координаты этих точек в уравнение и получим систему из двух линейных уравнений с тремя неизвестными

Положив D=1, найдем A= 1 и C= 2. Следовательно, уравнение плоскости имеет видx+2z+1=0.

Составить уравнение плоскости, проходящей через точку M(2;3;-4) параллельно плоскости yOz (перпендикулярно оси Ox).

Так как yOz||α, то уравнениеплоскости будет Ax+D=0. С другой стороны M Î α, поэтому 2A+D=0, D=-2A. Поэтому плоскость имеет уравнениеx-2=0.

УРАВНЕНИЕ ПЛОСКОСТИ В ОТРЕЗКАХ.

Рассмотрим плоскость, пересекающую все три координатные оси и не проходящую через начало координат. Пусть плоскость задана своим общим уравнением Ax+By+Cz+D=0, где ни один из коэффициентов не равен нулю.

Преобразуем это уравнение.

Ax+By+Cz=-D. Поделим полученное равенство на –D и запишем его в виде:

.

Тогда, обозначив , приходим к уравнению . Это уравнение и называется уравнением плоскости в отрезках.

Выясним геометрический смысл чисел a, b и c. Если положим y=z=0, то изуравнения x=a. Т.е. данному уравнению удовлетворяет точка с координатами (0; 0; 0). Следовательно, a – это длина отрезка, отсекаемого плоскостью на оси Ox. Аналогично, можно показать, что b и c – длины отрезков, отсекаемых рассматриваемой плоскостью на осях Oy и Oz.

Уравнением плоскости в отрезках удобно пользоваться для построения плоскостей.

Построить плоскость 2x+3y+6z-6=0. Приведём это уравнение к уравнению плоскости в отрезках: .

2x—y-4z-4=0. Рассмотрим еще один способ построения плоскостей. Для построения плоскости достаточно найти три какие-либо её точки, не лежащие на одной прямой. Удобнее всего определять точки пересечения плоскости с осями координат.

2x+5z-10=0. Плоскость параллельна оси Oy. Найдём точки пересечения с осями Ox и Oz.

Плоскость 3x+2y=0 проходит через ось Oz.