Угол между прямой и плоскостью: определение, примеры нахождения
Статья начинается с определение угла между прямой и плоскостью. В данной статье будет показано нахождение угла между прямой и плоскостью методом координат. Подробно будут рассмотрены решение примеров и задач.
Угол между прямой и плоскостью – определение
Предварительно необходимо повторить понятие о прямой линии в пространстве и понятие плоскости. Для определения угла между прямой и плоскостью необходимый несколько вспомогательных определений. Рассмотрим эти определения подробно.
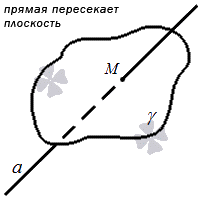
Прямая и плоскость пересекаются в том случае, когда они имеют одну общую точку, то есть она является точкой пересечения прямой и плоскости.
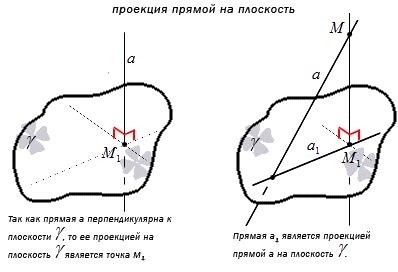
Прямая, пересекающая плоскость, может являться перпендикулярной относительно плоскости.
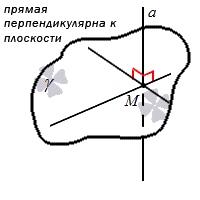
Прямая является перпендикулярной к плоскости, когда она перпендикулярна любой прямой, находящейся в этой плоскости.
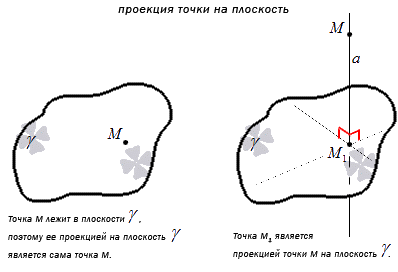
Проекция точки M на плоскость γ является сама точка, если она лежит в заданной плоскости, либо является точкой пересечения плоскости с прямой, перпендикулярной плоскости γ , проходящей через точку M , при условии, что она не принадлежит плоскости γ .
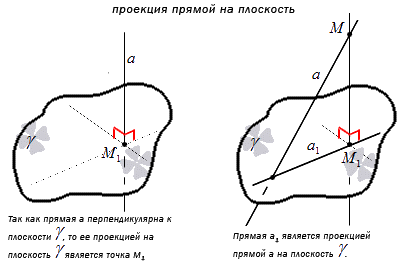
Проекция прямой а на плоскость γ — это множество проекций всех точек заданной прямой на плоскость.
Отсюда получаем, что перпендикулярная к плоскости γ проекция прямой имеет точку пересечения. Получаем, что проекция прямой a – это прямая, принадлежащая плоскости γ и проходящая через точку пересечения прямой a и плоскости. Рассмотрим на рисунке, приведенном ниже.
На данный момент имеем все необходимые сведения и данные для формулировки определения угла между прямой и плоскостью
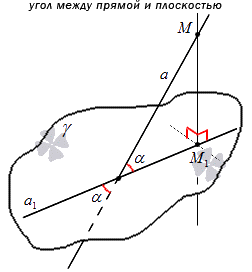
Углом между прямой и плоскостью называют угол между этой прямой и ее проекцией на эту плоскость, причем прямая не перпендикулярна к ней.
Определение угла, приведенное выше, помогает прийти к выводу о том, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми, то есть заданной прямой вместе с ее проекцией на плоскость. Значит, угол между ними всегда будет острым. Рассмотрим на картинке, приведенной ниже.
Угол, расположенный между прямой и плоскостью, считается прямым, то есть равным 90 градусов, а угол, расположенный между параллельными прямыми, не определяется. Бывают случаи, когда его значение берется равным нулю.
Нахождение угла между прямой и плоскостью
Задачи, где необходимо найти угол между прямой и плоскостью, имеет множество вариация решения. Ход самого решения зависит от имеющихся данных по условию. Частыми спутниками решения являются признаки подобия или равенства фигур, косинусы, синусы, тангенсы углов. Нахождение угла возможно при помощи метода координат. Рассмотрим его более детально.
Если в трехмерном пространстве вводится прямоугольная система координат О х у z , тогда в ней задается прямая a , пересекающая плоскость γ в точке M , причем она не перпендикулярна плоскости. Необходимо найти угол α , находящийся между заданной прямой и плоскостью.
Для начала необходимо применить определение угла между прямой и плоскостью методом координат. Тогда получим следующее.
В системе координат О х у z задается прямая a , которой соответствуют уравнения прямой в пространстве и направляющий вектор прямой пространства, для плоскости γ соответствует уравнение плоскости и нормальный вектор плоскости. Тогда a → = ( a x , a y , a z ) является направляющим вектором заданной прямой a , а n → ( n x , n y , n z ) — нормальным вектором для плоскости γ . Если представить, что у нас имеются координаты направляющего вектора прямой a и нормального вектора плоскости γ , тогда известны их уравнения, то есть заданы по условию, тогда есть возможность определения векторов a → и n → , исходя из уравнения.
Для вычисления угла необходимо преобразовать формулу, позволяющую получить значение этого угла при помощи имеющихся координат направляющего вектора прямой и нормального вектора.
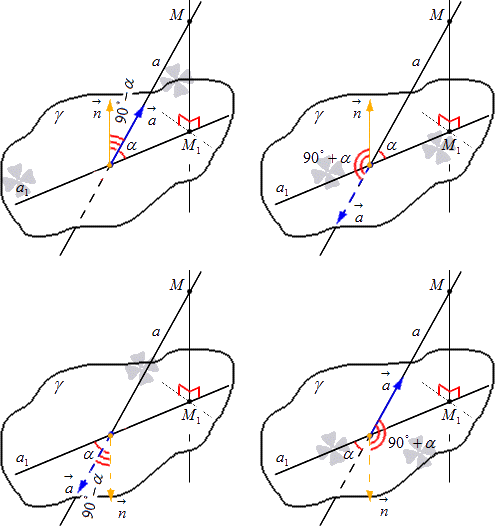
Необходимо отложить векторы a → и n → , начиная от точки пересечения прямой a с плоскостью γ . Существуют 4 варианта расположения этих векторов относительно заданных прямых и плоскости. Рассмотри рисунок, приведенный ниже, на котором имеются все 4 вариации.
Отсюда получаем, что угол между векторами a → и n → имеет обозначение a → , n → ^ и является острым, тогда искомый угол α , располагающийся между прямой и плоскостью, дополняется, то есть получаем выражение вида a → , n → ^ = 90 ° — α . Когда по условию a → , n → ^ > 90 ° , тогда имеем a → , n → ^ = 90 ° + α .
Отсюда имеем, что косинусы равных углов являются равными, тогда последние равенства записываются в виде системы
cos a → , n → ^ = cos 90 ° — α , a → , n → ^ 90 ° cos a → , n → ^ = cos 90 ° + α , a → , n → ^ > 90 °
Необходимо использовать формулы приведения для упрощения выражений. Тогда получим равенства вида cos a → , n → ^ = sin α , a → , n → ^ 90 ° cos a → , n → ^ = — s i n α , a → , n → ^ > 90 ° .
Проведя преобразования, система приобретает вид sin α = cos a → , n → ^ , a → , n → ^ 90 ° sin α = — cos a → , n → ^ , a → , n → ^ > 90 ° ⇔ sin α = cos a → , n → ^ , a → , n → ^ > 0 sin α = — cos a → , n → ^ , a → , n → ^ 0 ⇔ ⇔ sin α = cos a → , n → ^
Отсюда получим, что синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и нормальным вектором заданной плоскости.
Раздел нахождения угла, образованного двумя векторами, выявили, что этот угол принимает значение скалярного произведения векторов и произведения этих длин. Процесс вычисления синуса угла, полученного пересечением прямой и плоскости, выполняется по формуле
sin α = cos a → , n → ^ = a → , n → ^ a → · n → = a x · n x + a y · n y + a z · n z a x 2 + a y 2 + a z 2 · n x 2 + n y 2 + n z 2
Значит, формулой для вычисления угла между прямой и плоскостью с координатами направляющего вектора прямой и нормального вектора плоскости после преобразования получается вида
α = a r c sin a → , n → ^ a → · n → = a r c sin a x · n x + a y · n y + a z · n z a x 2 + a y 2 + a z 2 · n x 2 + n y 2 + n z 2
Нахождение косинуса при известном синусе позволительно, применив основное тригонометрическое тождество. Пересечение прямой и плоскости образует острый угол. Это говорит о том, что его значение будет являться положительным числом, а его вычисление производится из формулы cos α = 1 — sin α .
Выполним решение нескольких подобных примеров для закрепления материала.
Найти угол, синус, косинус угла, образованного прямой x 3 = y + 1 — 2 = z — 11 6 и плоскостью 2 x + z — 1 = 0 .
Для получения координат направляющего вектора необходимо рассмотреть канонические уравнения прямой в пространстве. Тогда получим, что a → = ( 3 , — 2 , 6 ) является направляющим вектором прямой x 3 = y + 1 — 2 = z — 11 6 .
Для нахождения координат нормального вектора необходимо рассмотреть общее уравнение плоскости, так как их наличие определяется коэффициентами, имеющимися перед переменными уравнения. Тогда получим, что для плоскости 2 x + z — 1 = 0 нормальный вектор имеет вид n → = ( 2 , 0 , 1 ) .
Необходимо перейти к вычислению синуса угла между прямой и плоскостью. Для этого необходимо произвести подстановку координат векторов a → и b → в заданную формулу. Получаем выражение вида
sin α = cos a → , n → ^ = a → , n → ^ a → · n → = a x · n x + a y · n y + a z · n z a x 2 + a y 2 + a z 2 · n x 2 + n y 2 + n z 2 = = 3 · 2 + ( — 2 ) · 0 + 6 · 1 3 2 + ( — 2 ) 2 + 6 2 · 2 2 + 0 2 + 1 2 = 12 7 5
Отсюда найдем значение косинуса и значение самого угла. Получим:
cos α = 1 — sin α = 1 — 12 7 5 2 = 101 7 5
Ответ: sin α = 12 7 5 , cos α = 101 7 5 , α = a r c cos 101 7 5 = a r c sin 12 7 5 .
Имеется пирамида, построенная при помощи значений векторов A B → = 1 , 0 , 2 , A C → = ( — 1 , 3 , 0 ) , A D → = 4 , 1 , 1 . Найти угол между прямой A D и плоскостью А В С .
Для вычисления искомого угла, необходимо иметь значения координат направляющего вектора прямой и нормального вектора плоскости. для прямой A D направляющий вектор имеет координаты A D → = 4 , 1 , 1 .
Нормальный вектор n → , принадлежащий плоскости А В С , является перпендикулярным вектору A B → и A C → . Это подразумевает то, что нормальным вектором плоскости А В С можно считать векторное произведение векторов A B → и A C → . Вычислим это по формуле и получим:
n → = A B → × A C → = i → j → k → 1 0 2 — 1 3 0 = — 6 · i → — 2 · j → + 3 · k → ⇔ n → = ( — 6 , — 2 , 3 )
Необходимо произвести подстановку координат векторов для вычисления искомого угла, образованного пересечением прямой и плоскости. получим выражение вида:
α = a r c sin A D → , n → ^ A D → · n → = a r c sin 4 · — 6 + 1 · — 2 + 1 · 3 4 2 + 1 2 + 1 2 · — 6 2 + — 2 2 + 3 2 = a r c sin 23 21 2
Уравнение плоскости, проходящей через точку и прямую онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и через данную прямую (точка не лежит на этой прямой). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через точку и прямую − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L:
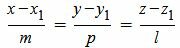 . . | (1) |
Задача заключается в построении уравнения плоскости α, проходящей через точку M0 и и через прямую L(Рис.1).
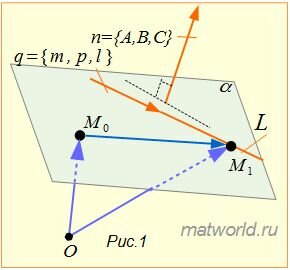 |
Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (2) |
Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
| A(x−x1)+B(y−y1)+C(z−z1)=0. | (3) |
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
Вычитая уравнение (3) из уравнения (2), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (5) |
Решая совместно уравнения (4) и (5) отностительно коэффициентов A, B, C получим такие значения A, B, C, при которых уравнение (2) проходит через точку M0 и через прямую (1). Для решения систему уравнений (4), (5), запишем их в матричном виде:
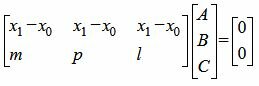 . . | (6) |
Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн.
Получив частное решение уравнения (6) и подставив полученные значения A, B, C в (2), получим решение задачи.
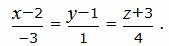 | (7) |
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0)=M0(1, 2, 5) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).
Вычитая уравнение (3) из уравнения (2), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (8) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
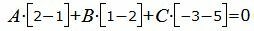 | (10) |
 | (11) |
Решим систему линейных уравнений (10) и (11) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
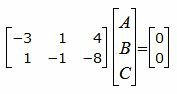 | (12) |
Решив однородную систему линейных уравнений (12) используя метод Гаусса, найдем следующее частное решение:
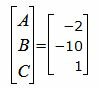 |
Подставляя значения коэффициентов A, B, C в уравнение плоскости (2), получим:
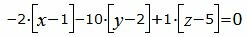 | (13) |
Упростим уравнение (13):
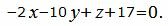 | (14) |
Ответ: Уравнение плоскости, проходящей через точку M0(1, 2, 5) и через прямую (7) имеет вид (14).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и через прямую L, заданной параметрическим уравнением:
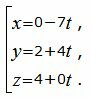 | (15) |
Решение. Приведем параметрическое уравнение (15) к каноническому виду:
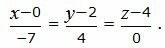 | (16) |
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (17) |
Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1)=(0, 2, 4). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
| A(x−x1)+B(y−y1)+C(z−z1)=0. | (18) |
Вычитая уравнение (18) из уравнения (17), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (19) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n должен быть ортогональным направляющему вектору прямой L :
| Am+Bp+Cl=0. | (20) |
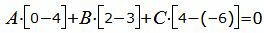 | (21) |
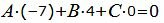 | (22) |
Решим систему линейных уравнений (21) и (22) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
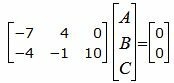 | (23) |
Решив однородную систему линейных уравнений (23) используя метод Гаусса, найдем следующее частное решение:
 |
Подставляя значения коэффициентов A, B, C в уравнение плоскости (17), получим:
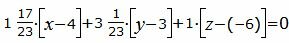 | (24) |
Упростим уравнение (24):
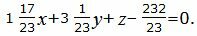 | (25) |
Уравнение плоскости можно представить более упрощенном виде, умножив на число 23.
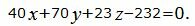 | (26) |
Ответ: Уравнение плоскости, проходящей через точку M0(4, 3, −6) и через прямую (16) имеет вид (26).
Уравнение плоскости, которая проходит через заданную прямую и заданную точку.
В этой статье собрана информация, необходимая для решения задачи составления уравнения плоскости, проходящей через заданную прямую и заданную точку. После решения этой задачи в общем виде мы приведем развернутые решения примеров на составление уравнения плоскости, которая проходит через заданную прямую и точку.
Навигация по странице.
Нахождение уравнения плоскости, проходящей через заданную прямую и заданную точку.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана прямая a и точка 

Сначала покажем, что существует единственная плоскость, уравнение которой нам требуется составить.
Напомним две аксиомы:
- через три различные точки пространства, не лежащие на одной прямой, проходит единственная плоскость;
- если две различные точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Из этих утверждений следует, что через прямую и не лежащую на ней точку можно провести единственную плоскость. Таким образом, в поставленной нами задаче через прямую a и точку M3 проходит единственная плоскость 
Теперь приступим к нахождению уравнения плоскости, проходящей через заданную прямую a и точку 
Если прямая a задана через указание координат двух различных точек М1 и М2 , лежащих на ней, то наша задача сводится к нахождению уравнения плоскости, проходящей через три заданные точки М1 , М2 и М3 .
Если же прямая a задана иначе, то нам сначала придется найти координаты двух точек М1 и М2 , лежащих на прямой a , а уже после этого записать уравнение плоскости, проходящей через три точки М1 , М2 и М3 , которое и будет искомым уравнением плоскости, проходящей через прямую a и точку М3 .
Разберемся, как найти координаты двух различных точек М1 и М2 , лежащих на заданной прямой a .
В прямоугольной системе координат в пространстве любой прямой линии соответствуют некоторые уравнения прямой в пространстве. Будем считать, что способ задания прямой a в условии задачи позволяет получить ее параметрические уравнения прямой в пространстве вида 




После этого нам останется лишь написать уравнение плоскости, проходящей через три различных и не лежащих на одной прямой точки 


Итак, мы получили уравнение плоскости, проходящей через заданную прямую a и заданную точку М3 , не лежащую на прямой a .
Примеры составления уравнения плоскости, проходящей через заданную точку и прямую.
Покажем решения нескольких примеров, в которых разберем рассмотренный метод нахождения уравнения плоскости, проходящей через заданную прямую и заданную точку.
Начнем с самого простого случая.
Напишите общее уравнение плоскости, которая проходит через координатную прямую Ox и точку 
Возьмем на координатной прямой Ox две различные точки, например, 

Теперь получим уравнение плоскости, проходящей через три точки М1 , М2 и М3 :
Это уравнение является искомым общим уравнением плоскости, проходящей через заданную прямую Ox и точку 

Если известно, что плоскость проходит через заданную точку и заданную прямую, и требуется написать уравнение плоскости в отрезках или нормальное уравнение плоскости, то следует сначала получить общее уравнение заданной плоскости, а от него переходить к уравнению плоскости требуемого вида.
Составьте нормальное уравнение плоскости, которая проходит через прямую 

Сначала напишем общее уравнение заданной плоскости. Для этого найдем координаты двух различных точек, лежащих на прямой 



Теперь мы можем составить общее уравнение прямой, проходящей через точку 

Осталось получить требуемый вид уравнения плоскости, умножив обе части полученного уравнения на нормирующий множитель 

Итак, нахождение уравнения плоскости, проходящей через заданную точку и заданную прямую, упирается в нахождение координат двух различных точек, лежащих на заданной прямой. В этом часто состоит основная сложность при решении подобных задач. В заключении разберем решение примера на составление уравнения плоскости, проходящей через заданную точку и прямую, которую определяют уравнения двух пересекающихся плоскостей.
В прямоугольной системе координат Oxyz задана точка 


Отталкиваясь от заданных уравнений двух пересекающихся плоскостей 

Процесс перехода от уравнений двух плоскостей, пересекающихся по прямой a , к параметрическим уравнениям прямой a подробно описан в статье уравнения прямой – уравнения двух пересекающихся плоскостей. Не будем на этом подробно останавливаться, а запишем лишь итоговый результат 




Таким образом, уравнение плоскости, проходящей через точку 


http://matworld.ru/analytic-geometry/uravnenie-ploskosti4-online.php
http://www.cleverstudents.ru/line_and_plane/plane_passes_through_line_and_point.html