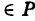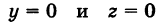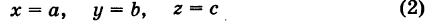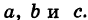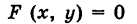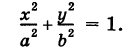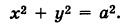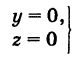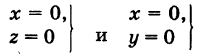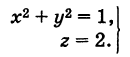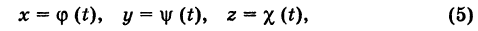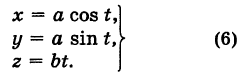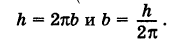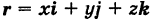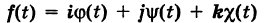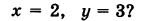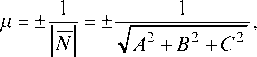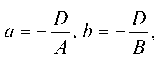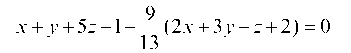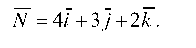Уравнение плоскости параллельной оси oz

Уравнение плоскости параллельной оси oz

Найти уравнение плоскости, параллельной оси Oz и проходящей через точки A(2, 3, -1) и B(-1, 2, 4).

Уравнение плоскости, параллельной оси Oz, имеет вид

(так как плоскость по условию задачи параллельна оси Oz, то в ее уравнении отсутствует координата z).

Если плоскость проходит через точку, то координаты этой точки удовлетворяют уравнению плоскости. Подставляя координаты точек A и B в уравнении (1), получим два уравнения:

Для определения коэффициентов A, B и D имеем систему двух однородных линейных уравнений с тремя неизвестными. Составляем матрицу коэффициентов этих уравнений

Тогда по формулам (25) получаем

Подставляя найденные значения A, B и C в (1), получим

После сокращения на t уравнение искомой плоскости приобретает вид

Проверьте правильность решения подстановкой в полученное уравнение сначала координат точки A, а потом координат точки B. Каждый раз в левой части должен получиться ноль.

Составить уравнение прямой параллельной оси oz

Составить уравнение прямой параллельной оси oz

Найти уравнение плоскости, параллельной оси Oz и проходящей через точки A(2, 3, -1) и B(-1, 2, 4).

Уравнение плоскости, параллельной оси Oz, имеет вид

(так как плоскость по условию задачи параллельна оси Oz, то в ее уравнении отсутствует координата z).

Если плоскость проходит через точку, то координаты этой точки удовлетворяют уравнению плоскости. Подставляя координаты точек A и B в уравнении (1), получим два уравнения:

Для определения коэффициентов A, B и D имеем систему двух однородных линейных уравнений с тремя неизвестными. Составляем матрицу коэффициентов этих уравнений

Тогда по формулам (25) получаем

Подставляя найденные значения A, B и C в (1), получим

После сокращения на t уравнение искомой плоскости приобретает вид

Проверьте правильность решения подстановкой в полученное уравнение сначала координат точки A, а потом координат точки B. Каждый раз в левой части должен получиться ноль.

Уравнения поверхности и линии в пространстве с примерами решения

Содержание:

Уравнения поверхности и линии в пространстве

Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если

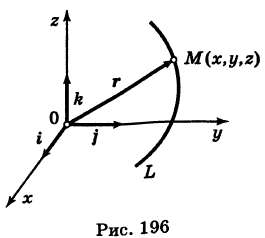
— уравнение поверхности Р (рис. 189), то при М(х, у, z)

Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.

Пример (уравнения координатных плоскостей):

Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,

— уравнение координатной плоскости Oyz. Аналогично,

— соответственно уравнения координатных плоскостей Oxz и Оху.

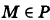
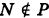
Формула обозначает, что точка М принадлежит Р. Формула обозначает, что точка N не принадлежит Р.

В более общем случае

— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные

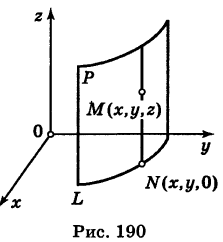
Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.

Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 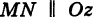(образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).

Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).

— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,

является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.

Пример (уравнение эллиптического цилиндра):

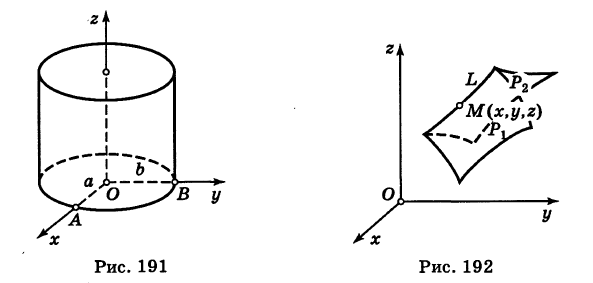
Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение

В частности, при а = b получаем уравнение кругового цилиндра

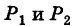
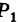
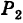
Линию L в пространстве можно задать как пересечение двух данных поверхностей (рис. 192). Точка , лежащая на линии L, принадлежит как поверхности так и поверхности , и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.

Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:

являющихся уравнениями поверхностей, определяющих данную линию.

Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки , координаты которых удовлетворяют обоим уравнениям системы (4).

Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.

Определение: Уравнениями линии в пространстве 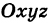называется такая пара уравнений между переменными , которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Пример (уравнения координатных осей):

Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому

— уравнения оси Ох. Аналогично,

— уравнения осей Оу и Oz соответственно.

Пример:

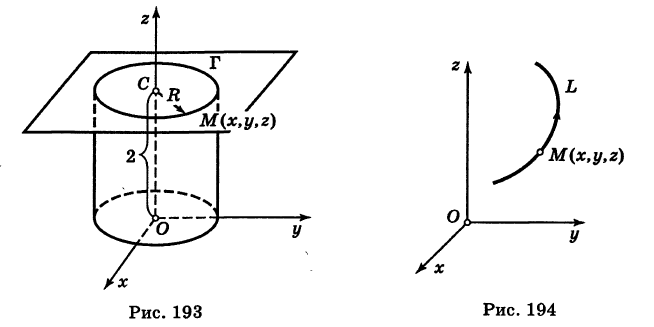
Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).

Решение:

Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть

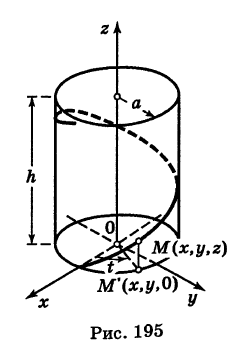
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем

где 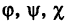— некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)> не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве.

Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.

Пример:

Написать уравнения винтовой линии радиуса а и шага 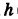(рис. 195).

Решение:

Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.

Приняв за параметр 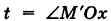и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь

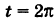
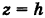
Для определения коэффициента пропорциональности b положим ; тогда . Следовательно,

Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем

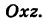
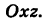
Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости . Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость — косинусоида.

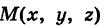
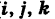
Текущую точку кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)

( — орты). Тогда из (5) получаем векторное уравнение линии

— так называемая вектор-функция скалярного аргумента t.

В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).

Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).

Пример:

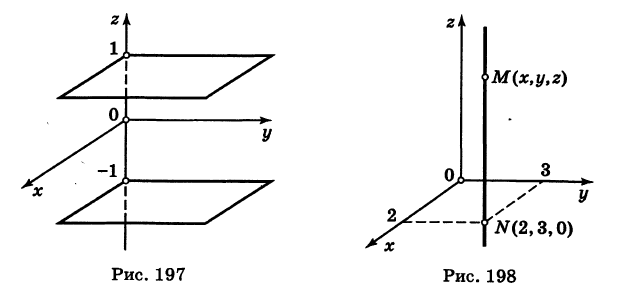
Какой геометрический образ соответствует уравнению

Решение:

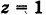
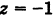
Из уравнения (8) получаем или . Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).

Пример:

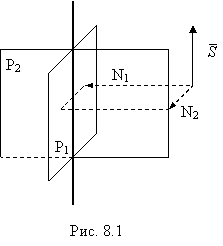
Какой геометрический образ соответствует паре уравнений

Решение:

Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).

• Общее уравнение плоскости
• Угол между плоскостями
• Понятие о производной вектор-функции
• Криволинейные интегралы
• Прямоугольная система координат на плоскости и ее применение
• Линии второго порядка
• Полярные координаты
• Непрерывность функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Электронная библиотека

1) Расстояние между двумя точками

2) Уравнение плоскости с нормальным вектором , проходящей через точку , есть , где — радиус-вектор текущей точки , – радиус-вектор точки M₀ .

В координатной форме эта плоскость имеет уравнение:

3) Расстояние точки от плоскости (*) равно:

4) Векторное уравнение прямой линии в пространстве: , где — текущий радиус-вектор точки прямой, — направляющий вектор прямой.

В координатной форме уравнение прямой имеет вид:

5) Прямая линия как пересечение плоскостей задается системой уравнений:

Направляющий вектор (рис. 8.1).

6) Уравнения прямой в параметрической форме:

7) Уравнение плоскости, проходящей через три точки:

Пример 18. Записать уравнение плоскости, отсекающей по осям координат соответственно отрезки а, b и с.

т.е. — уравнение плоскости в отрезках.

Пример 19. Записать уравнение плоскости, проходящей через точку М₀(2;-3;1) и имеющей нормальный вектор

Решение: Запишем уравнение плоскости, проходящей через данную точку М₀ и перпендикулярной данному вектору:

Пример 20. Найти величину отрезков, отсекаемых на осях координатной плоскостью 3х — 4у + 12z – 60 = 0.

Решение: приведём уравнение данной плоскости к уравнению в отрезках:

Пример 21. Записать уравнение прямой

и определить направляющие косинусы.

Решение: Имеем , следовательно, направляющий вектор

Пример 22. Записать уравнения прямой, проходящей через две несовпадающие точки

Решение: За направляющий вектор прямой можно принять

тогда уравнение искомой прямой будет:

Пример 23. Записать уравнение прямой, проходящей через точку М₀(3;-2;6) и параллельной оси Oz.

Решение: Поскольку прямая параллельна оси Oz, то и По каноническому уравнению получаем:

которые равносильны уравнениям:

Следовательно, искомая прямая перпендикулярна осям Ох и Оу.

Пример 24. Записать параметрические и канонические уравнения прямой, проходящей через точку М₀(5;-10;6) параллельно вектору

Решение: так как , то канонические уравнения прямой будут:

приравняв каждое из отношений параметру найдём параметрические уравнения:

8) Угол между плоскостями:

где — двугранный угол между плоскостями.

9) Условия параллельности и перпендикулярности плоскостей:

10) Угол между двумя прямыми в пространстве

11) Условия параллельности и перпендикулярности прямых:

12) Угол между прямой и плоскостью

13) Взаимное расположение прямой и плоскости:

а) прямая и плоскость пересекаются, если Am + Bn + ≠ 0;

б) перпендикулярны, если ,

в) параллельны, если , ( );

г) совпадают, если , .

Пример 25: Найти угол между плоскостями 2x-3y-2z+5=0 и 3x-5y+z-3=0.

Пример 26: Найти угол между прямой x = -2 — t, y = 3 — t, z = -3 + 2t и плоскостью 4x — 8y + 4z – 18 = 0.

Решение: Имеем , найдем

Пример 27. Найти проекцию точки M(2;-1;3) на плоскость 3x — 2y + 4z + 15 = 0.

Решение: Проекция точки на плоскость есть основание перпендикуляра, опущенного из данной точки на плоскость 3x-2y+4z+15=.

Если провести прямую через этот перпендикуляр, то направляющим вектором этой прямой будет вектор , так как он совпадает с нормальным вектором данной плоскости. Следовательно, прямая, проходящая через точку M(2,-1,3) будет:

Подставим эти выражения в уравнения плоскости, будем иметь:

При этом значении t из уравнения прямой получаем:

Следовательно, точка M * ( ) – искомая проекция.

Поверхности второго порядка

1) Цилиндрические поверхности:

а) с образующими параллельными оси OZ: F(x,y) = 0;

б) с образующими параллельными оси OX: F(y,z) = 0;

в) с образующими параллельными оси OY: F(x,z) = 0.

Пример 28: Указать, какие поверхности заданы уравнениями:

а) в уравнении отсутствует явно переменная z, следовательно, имеем цилиндрическую поверхность с образующими параллельными оси OZ, направляющей служит окружность x 2 + y 2 = 4 (рис. 8.2, а) – прямой круговой цилиндр;

б) y = x 2 – параболический цилиндр, с образующими параллельными оси OZ, y = x 2 — направляющая (рис. 8.2, б);

в) x 2 / 9 + z 2 / 4 = 1 – эллиптический цилиндр, так как направляющая есть эллипс; образующие параллельные оси OY (рис. 8.2, в);

г) x 2 — y 2 = 4 – гиперболический цилиндр с образующими, параллельными оси OZ (рис. 8.2, г).

2) Поверхности вращения:

а) поверхность, образованная вращением линии l, x = x(z), y = y(z) вокруг оси OZ, задается уравнением x 2 + y 2 = x 2 (z) + y 2 (z);

б) поверхность, образованная вращением линии x = x₁(у), z = z₁(у) вокруг оси ОУ, задается уравнением ;

в) поверхность, образованная вращением линии y = y₂(x), z = z₂(x) вокруг оси ОХ, задается уравнением .

Пример 29: Записать уравнения поверхностей вращения, если:

а) линия z = y 2 вращается вокруг оси OZ;

б) линия x = y вращается вокруг оси ОУ.

Решение: а) так как линия z = y 2 вращается вокруг оси OZ, то каждая ее точка описывает окружность радиуса с центром на оси OZ. Следовательно, в уравнении линии надо заменить y на , получим — параболоид вращения с осью вращения OZ (рис. 8.2, е).

Поверхности второго порядка

2) Уравнение трехосного эллипсоида с полуосями a, b и с:

3) Уравнение однополосного гиперболоида:

4) Уравнение двухполосного гиперболоида:

5) Уравнение конуса второго порядка:

6) Эллиптический параболоид:

7) Гиперболический параболоид (“седло”):

8) — пара пересекающихся плоскостей.

9) — пара параллельных плоскостей.

10) Уравнение параболоида вращения вокруг оси OZ:

Замечание: Вид поверхностей, соответствующих приведенным уравнениям, легко получить методом “сечений”.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

1.3.2. Аналитическая геометрия в пространстве

1. Всякая плоскость в координатном пространстве OXYZ имеет векторное уравнение следующего вида: r ¦ п = p. Здесь

r = xi + yj + zk — радиус-вектор текущей точки плоскости

M(x, у, z); п = i cosa + j cos b + k cosg — единичный вектор, имеющий направление перпендикуляра, опущенного на плоскость из начала координат, a, b, g — углы, образованные этим перпендикуляром с осями координат OX, OY, OZ, и р — длина этого перпендикуляра.

При переходе к координатам это уравнение принимает вид xcos a + ycos b + zcos g — p = 0 (нормальное уравнение плоскости).

2. Уравнение всякой плоскости может быть записано также в виде Ах + Ву +Cz + D = 0 (общее уравнение). Здесь А, B, C можно рассматривать как координаты некоторого вектора

N = Ai + Bj + Ck, перпендикулярного к плоскости. Для приведения общего уравнения плоскости к нормальному виду все члены уравнения надо умножить на нормирующий множитель

где знак перед радикалом противоположен знаку свободного члена D в общем уравнении плоскости.

3. Частные случаи расположения плоскости, определяемой уравнением Ах + Ву +Cz + D = 0:

А = 0; плоскость параллельна оси ОХ;

В = 0; плоскость параллельна оси О^

C = 0; плоскость параллельна оси ОZ;

D = 0; плоскость проходит через начало координат;

А = В = 0; плоскость перпендикулярна оси ОZ (параллельна плоскости ХОY);

А = C = 0; плоскость перпендикулярна оси ОY (параллельна плоскости ХОZ);

В = C = 0; плоскость перпендикулярна оси ОХ (параллельна плоскости YОZ);

А = D = 0; плоскость проходит через ось ОХ;

В = D = 0; плоскость проходит через ось OY;

C = D = 0; плоскость проходит через ось OZ;

А = В = D = 0; плоскость совпадает с плоскостью XOY (z = 0);

А = C = D = 0; плоскость совпадает с плоскостью XOZ (у = 0);

B = C = D = 0; плоскость совпадает с плоскостью YOZ (х = 0).

Если в общем уравнении Ах + By +Cz + D = 0 коэффициент D ф 0, то, разделив все члены уравнения на — D, можно уравнение

плоскости привести к виду^ здесь

. Это уравнение плоскости называется уравнением в отрезках: в нем а — абсцисса точки пересечения плоскости с осью OX, b и с — соответственно ордината и аппликата точек пересечения плоскости с осями OY и OZ.

4. Угол j между плоскостями А1х + В1У + Qz + D1 = 0 и А2х + В2У +C2z + D2 = 0 определяется по формуле

Условие параллельности плоскостей:

Условие перпендикулярности плоскостей:

5. Расстояние от точки М0(х0; у0; z0) до плоскости, определяемой уравнениемНаходится по формуле

Оно равно взятому по абсолютной величине результату подстановки координат точки в нормальное уравнение плоскости; знак результата этой подстановки характеризует взаимное расположение точки M0 и начала координат относительно данной плоскости: этот знак положителен, если точка M0 и начало координат расположены по разные стороны от плоскости, и отрицателен, если они расположены по одну сторону от плоскости.

6. Уравнение плоскости, проходящей через точку М0(х0; у0; z0)

и перпендикулярной к вектору N = Ai + Bj + Ck, имеет вид А(х — х0) + B(y — у0) + C(z — z0) = 0. При произвольных А, В и C последнее уравнение определяет некоторую плоскость, принадлежащую к связке плоскостей, проходящих через точку М0. Его часто поэтому называют уравнением связки плоскостей.

7. Уравнение А1х + B1y +C1z + D1 + А(А2х + B^y +C2z + D2) = 0 при произвольном I определяет некоторую плоскость, проходящую через прямую, по которой пересекаются плоскости, определяемые уравнениями

некоторую плоскость, принадлежащую пучку плоскостей, проходящих через эту прямую (в силу чего такое уравнение часто называют уравнением пучка плоскостей). Если плоскости, определяемые уравнениями I и II, параллельны, то пучок плоскостей превращается в совокупность плоскостей, параллельных этим плоскостям.

8. Уравнение плоскости, проходящей через три заданные точки M1(r 1Х M1(Jj), M3(r 3) (Л = x1i + yd + z1k; r2 = x2i + У2 j + z2k; r3 = x3i + y3 j + z3 к), проще всего найти из условия компланарности векторов r — T1, r2 — rl, r3 — rl, где r = xi + yj+zk — радиус-вектор текущей точки искомой плоскости M:

или в координатной форме:

Пример 1.21. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + у + 5z — 1 = 0, 2x + 3у — z + 2 = 0 и через точку М(3, 2, 1).

Решение. Воспользуемся уравнением пучка плоскостей

Значение I определяем из условия, что координаты точки М должны удовлетворять этому уравнению:

Получаем искомое уравнение в виде:

или, умножая на 13 и приводя подобные члены, в виде:

Пример 1.22. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + 3у + 5z — 4 = 0 и X — у — 2z + 7 = 0 и параллельной оси оу.

Решение. Воспользуемся уравнением пучка x + 3у + 5z — 4 + + l(x — у — 2z + 7) = 0, преобразуем уравнение к виду (1 + Х)х + (3 -1)у + (5 — 2l)z + (71 — 4) = 0.

Так как искомая плоскость параллельна оси ординат, то коэффициент при у должен равняться нулю, т. е. 3 — l = 0, I = 3. Подставив значение I в уравнение пучка, получаем

Пример 1.23. Найти уравнение плоскости, проходящей через точки М (2; -1; 4) и N(3; 2; -1) перпендикулярно к плоскости X + у + z — 3 = 0.

Решение. Воспользуемся уравнением плоскости, проходящей через первую из данных точек:

Условие прохождения этой плоскости через вторую точку и условие перпендикулярности определяются равенствами:

Исключая коэффициенты А, В и C из системы уравнений

получаем искомое уравнение в виде:

Пример 1.24. Из точки P(2; 3; -5) на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.

Решение. Основаниями перпендикуляров, опущенных на координатные плоскости, будут следующие точки М1(2; 3; 0), М2(2; 0; -5), М3(0; 3; -5). Напишем уравнение плоскости, проходящей через точки М1, М2, М3, для чего воспользуемся уравнением

Пример 1.25. Составить уравнение плоскости, проходящей через точку M (2; 3; 5) и перпендикулярной к вектору

Решение. Достаточно воспользоваться уравнением плоскости, проходящей через данную точку и перпендикулярной к данному вектору:

1. Прямая может быть задана уравнениями 2-х плоскостей

пересекающихся по этой прямой.

2. Исключив поочередно х и у из предыдущих уравнений, получим уравнения х = аz + с, у = bz + d. Здесь прямая определена двумя плоскостями, проектирующими ее на плоскости хoz и yoz.

3. Если даны две точки M(x1, у1, z1) и N(x2, у2, z2), то уравнения прямой, проходящей через них, будут иметь вид:

4. Так называемые канонические уравнения

определяют прямую, проходящую через точку M(x1, у1, z1)

и параллельную вектору S = li + mj + nk. В частности, эти уравнения могут быть записаны в виде:

где a, b и g — углы, образованные прямой с осями координат.

5. От канонических уравнений прямой, вводя параметр t, нетрудно перейти к параметрическим уравнениям прямой:

6. Угол между двумя прямыми, заданными их каноническими

деляется по формуле

перпендикулярности двух прямых:

условие параллельности двух прямых:

7. Необходимое и достаточное условие расположения двух прямых, заданных их каноническими уравнениями, в одной плоскости (условие компланарности двух прямых):

Если величины /1, т\, П1 непропорциональны величинам /2, m2, «2, то указанное соотношение является необходимым и достаточным условием пересечения двух прямых в пространстве.

условие параллельности прямой и плоскости: условие перпендикулярности прямой и плоскости:

Определяется по формуле

9. Для определения точки пересечения прямой

С плоскостью Ах + Ву + Cz + D = 0 нужно решить совместно их уравнения, для чего следует воспользоваться параметрическими уравнениями прямой x = /t + X0, у = mt + у0, z = nt + z0:

а) если А/ + Вт + Cn ф 0, то прямая пересекает плоскость в одной точке;

б) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D ф 0, то прямая параллельна плоскости;

в) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D = 0, то прямая лежит в плоскости.

Пример 1.26. Привести к каноническому виду уравнения прямой 2х — у + 3z — 1 = 0 и 5х + 4у — z — 7 = 0.

Решение. Исключив вначале у, а затем z, получим:

Если разрешим каждое из уравнений относительно х, то будем иметь:

отсюда

Второй способ: найдем вектор S = li + mj + nk, параллельный искомой прямой. Так как он должен быть перпендикулярен к нормальным векторам заданных плоскостей N1 = 2i — j + 3k и N2= 5i + 4 j — k, то за него можно принять векторное произведение векторов N1 и N2.

Таким образом, l = -11; m = 17; n = 13.

За точку M1(x1, у1, z1), через которую проходит искомая прямая, можно принять точку пересечения ее с любой из координатных плоскостей, например с плоскостью yoz. Т ак как при этом x1 = 0, то координаты y1 и z1 этой точки определятся из системы уравнений заданных плоскостей, если в них положить х = 0:

Решая эту систему, находим у1 = 2; z1 = 1.

Итак, искомая прямая определяется уравнениями:

Мы получили прежний ответ.

Пример 1.27. Построить прямую

Решение. Искомую прямую можно построить как линию пересечения плоскостей. Для этого напишем уравнения плоскостей, которыми определена прямая, в отрезках на осях:

Пример 1.28. Из начала координат опустить перпендикуляр на прямую

Решение. Составим уравнение плоскости, проходящей через начало координат и перпендикулярной заданной прямой: 2х + 3у + z = 0. (Для этой плоскости можно принять А = l; B = m; C = n; D = 0; использовано условие перпендикулярности прямой и плоскости, см. п. 8 введения к настоящему разделу).

Найдем точку пересечения этой плоскости и данной прямой. Параметрические уравнения прямой имеют вид:

Построив данные плоскости, мы получим искомую прямую как линию пересечения этих плоскостей (рис. 20).

Для определения t имеем уравнение:

Остается составить уравнения прямой, проходящей через начало координат и через точку М (см. п. 3 введения к настоящему разделу):

Пример 1.29. В уравнениях прямойОпределить

параметр n так, чтобы эта прямая пересекалась с прямой

, и найти точку их пересечения.

Решение. Для нахождения параметра n используем условие пересечения 2-х прямых:

Следовательно, уравнения пересекающихся прямых таковы: искомой:

Для вычисления координат точки пересечения этих прямых выразим из первого уравнения х и у через z: х = 2z, у = -3z. Подставляя их значения в равенствоИмеем,

отсюда z = 1. Зная z, находим х и у: х = 2z = 2, у = -3z = -3. Следовательно M(2; -3; 1).

Пример 1.30. Прямая задана каноническими уравнениями

Составить общие уравнения этой прямой.

Решение. Канонические уравнения прямой можно записать в виде системы двух независимых уравнений:

Получили общие уравнения прямой, которая теперь задана пересечением 2-х плоскостей, одна из которых 5х — 3у — 13 = 0 параллельна оси Oz, а другая х + 3z — 11 = 0 параллельна оси Oy.

Пример 1.31. Найти координаты точки M, делящей попалам отрезок прямой

заключенный между плоскостями хoz и xoy.

Решение. Найдем точку А пересечения прямой с плоскостью хoz, полагая в уравнениях прямой у = 0. Тогда получим:

отсюда x = 2,6; z = 2,8. Тогда А(2,6; 0; 2,8).

отсюда X = 11, у = 14, или В(11; 14; 0).

Определяем координаты точки М, делящей отрезок АВ пополам:

Следовательно, координаты искомой точки М будут: М(6,8; 7; 1,4).

Пример 1.32. Составить уравнение плоскости, проходящей через прямую

Решение. Составим уравнение пучка плоскостей, проходящих через первую из данных прямых:

которое делим на а ф 0, и пусть b /а = I:

Аналогично, полагая в уравнениях прямой z = 0, найдем координаты точки В пересечения прямой с плоскостью хоу:

В этом пучке нужно выбрать плоскость, параллельную 2-й данной прямой. Из условия параллельности плоскости и прямой, имеем:

Подставляя I = 1 в уравнение пучка плоскостей, получим: Тогда искомое уравнение плоскости будет:

Пример 1.33. Дана прямая Найти ее проекцию на плоскость

Решение. Нужно найти плоскость, которая проходит через данную прямую перпендикулярно к данной плоскости; тогда искомая проекция определится как пересечение этой плоскости с данной.

Составим уравнение пучка плоскостей, проходящих через данную прямую:

Эта плоскость должна быть перпендикулярной к данной плоскости, что можно записать как:

Тогда уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости, будет:

Проекция данной прямой на данную плоскость определяется как прямая пересечения плоскостей:

Запишем эту прямую в каноническом виде. Найдем на прямой какую-либо точку. Для этого положим, например х0 = 1, и система запишется в виде:

Отсюда, у0 = 1, z0 = 0, т. е. точка M(1; 1; 0) принадлежит искомой прямой.

Направляющий вектор прямой S = (l; m; n) найдем из того условия, что он перпендикулярен нормальным векторам

N1 = (2; -3; -2) и N2 = (5; 2; 2) плоскостей, определяющих искомую прямую.

В качестве S берем векторное произведение векторов N1 и N2 , т. е.

Тогда искомое уравнение в каноническом виде будет: